基于改进遗传算法的冷却塔出塔水温的预测
2016-07-05李启本周明昊丁晟琪
李启本,周明昊,丁晟琪
(1.国网上海市电力公司松江供电公司,上海 200090;2.上海市政交通设计研究院有限公司,上海 200090)
基于改进遗传算法的冷却塔出塔水温的预测
李启本1,周明昊2,丁晟琪1
(1.国网上海市电力公司松江供电公司,上海200090;2.上海市政交通设计研究院有限公司,上海200090)
摘要:以迈克尔焓差理论为基础,建立自然通风逆流湿式冷却塔两个平衡组成的方程,对平衡方程涉及到的参数进行分析,将出塔水温的求解问题转换为方程组的求解问题。提出一种改进的遗传算法,应用到冷却塔出塔水温的计算中,并对适应度函数进行实时修正,实现对出塔水温的在线预测,并且准确度较高,对水泵的调节具有一定的指导意义。
关键词:冷却塔;出塔水温;遗传算法;在线预测
冷却塔是电厂冷端系统主要设备之一,其作用是冷却携带废热的循环水,将热量散入大气,并将冷却后的水循环利用。自然通风逆流湿式冷却塔通常采用双曲线形,在我国电力部门应用最多。自然通风逆流湿式冷却塔的冷却效果的好坏直接影响凝汽器的真空度,从而影响机组运行的稳定性和安全性。此外,在火电厂循环水系统的节能分析以及优化运行的大量研究中,都把凝汽器的真空度作为研究切入点[1-3]。冷却塔出塔水温也是凝汽器的进口温度,直接影响凝汽器的真空度,从而影响机组测出力。一般情况下,300MW机组的出塔水温降低1℃,凝汽器的真空将会提高400~500Pa,煤耗将下降1.0~1.5g/(kW·h)[4]。因此,预测冷却塔出塔水温是确保机组安全稳定运行和循环水系统优化运行的关键。
自然通风逆流湿式冷却塔的出塔水温的计算主要涉及到冷却塔空气的动力计算和热力计算。由于塔内外空气密度大小的不同,存在压差,会产生抽力。外部的空气进入冷却塔,在穿过雨区、填料、配水系统、收水器,并最后从塔口排出时,会产生阻力,这部分的阻力要靠冷抽力来克服,因此阻力和抽力平衡[5]。冷却塔的热力计算,应用较普遍的计算方法是“火力发电厂水工设计技术规定”推荐的焓差法[6]。对冷却塔出塔水温的预测已有大量研究,未考虑到汽轮机的排汽量。汽轮机的排汽量直接影响循环水在凝汽器中的温升,从而会对冷却塔的进塔水温产生影响,若不考虑汽轮机排汽量无疑会使计算结果与实际产生较大误差。基于以上的研究基础,本文提出了一种改进的遗传算法,并将其应用到冷却塔的出塔水温的计算中。以某地一台300MW机组配备的冷却塔为研究对象,应用提出的遗传算法求解出塔水温,预测了该塔在某一段时间内不同的气象条件、不同的负荷、不同的水流量下的冷却塔的出塔水温。
1冷却塔的热力特性
冷却塔内空气与循环水之间的热量交换有接触散热、蒸发散热和辐射散热这3种形式。辐射散热量很小,可以忽略不计。在热量交换的过程中,除了有热传递之外还会产生质量的损失。麦克尔引入了焓的概念,包括了散热和散质,减少了计算参数。冷却塔热力计算的基本方程:
(1)
式中K——蒸发水量系数;
βxv——容积散质系数,kg/(m3·s);
V——淋水面积,m3;
Q——冷却水流量,kg/s;
Cw——水的比热,kJ/(kg·℃);
hθ——空气的比焓,kJ/kg;
h″t——温度为水的温度t时的饱和空气比焓,kJ/kg;
t1,t2——循环水进塔、出塔的温度,℃;
dt——进、出微单元的温差。
蒸发水量散热系数可计算为:
K=1-t2/[586-0.56(t2-20)]
(2)
1.1冷却塔特性数的计算
式(1)左端表示塔的特性参数,反应的是冷却塔的冷却能力,其大小是冷却塔冷却效果好坏的标志,与冷却塔的塔型、淋水面积、冷却塔所处的环境有关,计算公式如下:
(3)
式中A、m——试验常数;
λ——气水比。
(4)
式中vm——进塔风速,m/s;
Fm——淋水面积,m2;
ρ1——进塔空气密度,kg/m3;
Dw——冷却水流量,kg/s。
(5)
式中ρ1——进塔空气密度,kg/m3;
φ——相对空气湿度;
Pgq——干球温度对应的饱和蒸汽压力,kPa;
P——当前大气压力,kPa。
饱和蒸汽压力可由以下公式计算出:
P=1033.590 624-3142.305/T-8.2lgT+0.002 480 4T/1 000
(6)
式中T——工质当前热力学温度,K。
1.2冷却塔冷却数的计算
式(1)右端是冷却塔的冷却数,用N表示。冷却数的计算是一个简单的积分过程,有辛普逊积分法、饱和焓用抛物线方程的积分法和平均焓差法。采用辛普逊积分法计算公式:

(7)
式中h″2,h″m,h″1——出塔水温t2、平均水温tm和进塔水温t1时的饱和空气焓值;
h1,hm,h2——进塔空气、平均状态空气及出塔空气比焓;
Δt——进出塔水温差。
h″2、h″m、h″1、h1可查表或由湿空气的焓值计算:
(8)
(9)
hm=(h1+h2)/2
(10)
式中t——湿空气的温度,℃;
pt——湿空气温度对应的饱和蒸汽压力,kPa;
φ——相对空气湿度。
2冷却塔的空气动力计算
2.1塔的抽力
冷却塔的抽力是靠塔筒产生的,塔外的冷空气进入塔内,在填料和配水装置内进行热交换后,变为饱和的热空气,密度降低,他内外产生压力,即抽力。
Fd=Heg(ρ1-ρ2)
(11)
式中Fd——冷却塔抽力,Pa;
He——冷却塔有效高度,m;
ρ1,ρ2——塔外、塔内空气密度,kg/m3。
2.2冷却塔的阻力
塔外的冷空气进入冷却塔内要经过雨区、调料、配水系统、收水器,最终从塔出口排到大气,在此过程中产生的阻力,即塔的阻力Fr可计算为:
(12)
ρm=(ρ1+ρ2)/2
(13)
ξa=(1-3.47ε+3.65ε2)
(14)
ξh=6.72+0.645D+3.5q
+1.43vm-60.61ε-0.36vmD
(15)
(16)
ξ=ξa+ξb+ξe
(17)
式中ξ——塔的阻力系数;v0——填料断面的气流速度,m/s;
ρm——填料断面空气密度;
ξa——从塔的进风口至塔喉部的阻力系数(不包括雨区临水阻力);
ξb——淋水时雨区阻力系数;
ξf——淋水时的填料、储水器、配水系统的阻力系数;
ε——塔进风口面积(按进风口上缘直径计算的进风口环向面积)与进风口上缘塔面积之比,0.35<ε<0.45;
D——淋水填料底部塔内径,m;
vm——临水填料计算断面的平均风速,m/s;
ξe——塔筒出口阻力系数;
Fm——冷却塔淋水面积,m2;
Fe——塔筒出口面积,m2;
q——淋水密度,kg/m2。
3进塔水温、出塔水温的计算
将冷却塔的热力计算和空气动力计算所涉及到的参数分别归类为气象参数、冷却塔特性参数和工况条件3类,见表1。

表1 冷却塔参数
在冷却塔热力计算和塔内空气动力计算涉及到的参数中,气象参数可由气象部门或电厂的测点测得,冷却塔特性参数由冷却塔设计者提供,工况条件中除了进塔风速外,电厂都有相关的测点实时测量。当汽轮机稳定工作在某一负荷时,冷却塔的特性数与冷却数、塔的总阻力与抽力分别平衡,即N=Ω、Fd=Fr[7]。当汽轮机的负荷改变时,循环水泵的运行模式要作出相应的调整,循环水流量大小也会随之变化,从而影响冷却塔出塔空气密度,进而改变冷却塔的进塔风速[8]。将冷却塔出塔水温的计算简化成一个求解二元方程组的问题,即特性数与冷却数、塔的总阻力与抽力的平衡,两个未知数为进塔风速vm和出塔水温t2。
在参与调峰的电厂中,汽轮机的排汽量是根据电厂日负荷曲线变化的,排汽量的变化是一个缓慢的过程,在此过程中冷却塔的出塔水温也会产生变化,但当排汽量最终稳定后,出塔水温也将会稳定在一个特定值。冷却塔特性数与当前的大气温度、相对湿度、大气压力、进塔风速、淋水面积、循环水流量有关,本算法目的是求稳定后的出塔水温,假设当前为t1时刻,对t2时刻出塔水温的预测程序流程如图1所示。

图1 遗传算法出塔的预测
Step1:程序开始。
Step2:读取参数。读取冷却塔的特性参数、气象参数和工况条件。其中工况条件中汽轮机的排汽量和气象参数为待预测时刻(t2时刻)的值,排汽量可以根据电网提供的电厂日负荷曲线确定,气象参数可以通过当地的气象部门获得。
Step3:初始化。出塔水温初始化:种群大小赋值150,染色体长度15,采用二进制编码,为了提高计算的精确度,减少计算时间,出塔水温的取值范围根据当前出塔水温的值来确定,若读取的当前出塔水温为t21,出塔水温的种群范围为[t21-5,t21+5]。进塔风速初始化:根据当地气象部门提供的实时风速,确定进塔风速种群范围确定为[0,2.5m/s],种群大小初始化为150,染色体长度为15,采用二进制编码。
Step4:确定进塔水温。根据凝汽器的热平衡方程可求得冷却水温升Δt=520/m=520Dc/Dw,其中,m为凝汽器的冷却倍率;Dc、Dw分别为进入凝汽器的蒸汽量和循环冷却水量。因此在获得汽轮机的排汽量与循环水流量后,冷却塔进塔温度可以表示为t1=t2+Δt。
Step5:遗传代数初始化。确定遗传代数为40。
Step6:确定目标函数
Fi=(Fri-Fdi)2+(Ni-Ωi)2
(18)
Step7:确定适应度函数
(19)
Step8:计算特性数、冷却数、抽力、阻力。
Step9:计算目标函数。带入式(18)计算目标函数值。
Step10:计算适应度函数。将目标函数值带入式(19)计算适应度函数值。
Step11:选择最优个体。比较种群的适应度函数值,挑选出适应度值最大的个体。
Step12:在允许误差之内。将最大个体的特性数、冷却数、抽力、阻力带入误差公式:Error=|Fr-Fd|+|N-Ω|,判断误差是否在允许范围之内,如果在允许范围之内,执行Step15,否则执行Step13。
Step13:是否满足最大遗传代数。为了避免程序无法寻找到最优解时陷于死循环中,判断当前是否为最大遗传代数,如果是,执行Step15,如果否转到Step14。
Step14:遗传操作。对种群进行选择、交叉、变异操作。当个体的适应度值f’与种群中的最大适应度值fmax相等时,该个体变异交叉概率为零,即不需要变异交叉操作,直接保留该个体遗传到下一代;当f’在fmax和favg之间时,Pc和Pm根据当前个体的适应度值做自适应调,若当前个体的适应度值较大,Pc和Pm便较小,若当前个体适应度值较大,则Pc和Pm相对较大;若f’比种群平均适应度小,说明当前个体较不满足遗传所需的条件,因此对其进行强制的变异交叉操作。交叉操作中,将个体xi的前n位与个体xi+1的前n位进行互换。采用单点或双点的变异操作,由于本文采用二进制编码,对变异个体的相应位进行取反。
交叉变异概率可计算为:
(20)
Step15:记录最优解,存储最优的个体。
Step16:结束。
遗传算法应用在某电厂的冷却塔中,结果如图2至图5所示。在图2至图5中,“△”、“○”、“□”、“+”分别是每一代遗传中最大适应度的个体对应的特性数、冷却数、抽力与阻力。遗传算法每一代特性数与冷却数的误差与抽力与阻力的误差如图6所示。

图2 冷却数与特性数的平衡点

图3 冷却数与特性数的平衡点局部图

图4 抽力与阻力的平衡点

图5 抽力与阻力平衡点局部图
从图6中可看出,算法收敛速度较快,程序在运行中的效率较高,能够迅速的找到满足两个平衡条件的进塔风速和出塔水温。但在实际应用中,由于各种各样的因素,冷却塔的特性数、冷却数、抽力与阻力会与理论计算值存在着一些差异,这会导致冷却塔出塔水温的预测结果产生误差。
图7是一种对出塔水温实时在线预测方案。步骤①读取当前t1时刻的工况条件和气象参数作为算法的输入,求出当前冷却塔的出塔水温,并与当前测点测得的冷却塔出塔水温进行比较,若两者误差在允许范围之内,则输出当前的适应度函数,并将其作为预测水温算法中的适应度函数,若误差不在允许范围之内,则将误差作为反馈信息对适应度函数进行修正,直至误差在设置范围之内;步骤②根据电网提供的负荷曲线和气象部门提供的气象参数,获得t2时刻工况条件和气象参数,修正后的适应度函数更新到预测算法中,求解t2时刻的出塔水温。
4出塔水温的计算
某地的大气压力为1.003×19=105Pa,抄录当地某一天的气温和相对湿度如图8图9所示。

图8 温度曲线
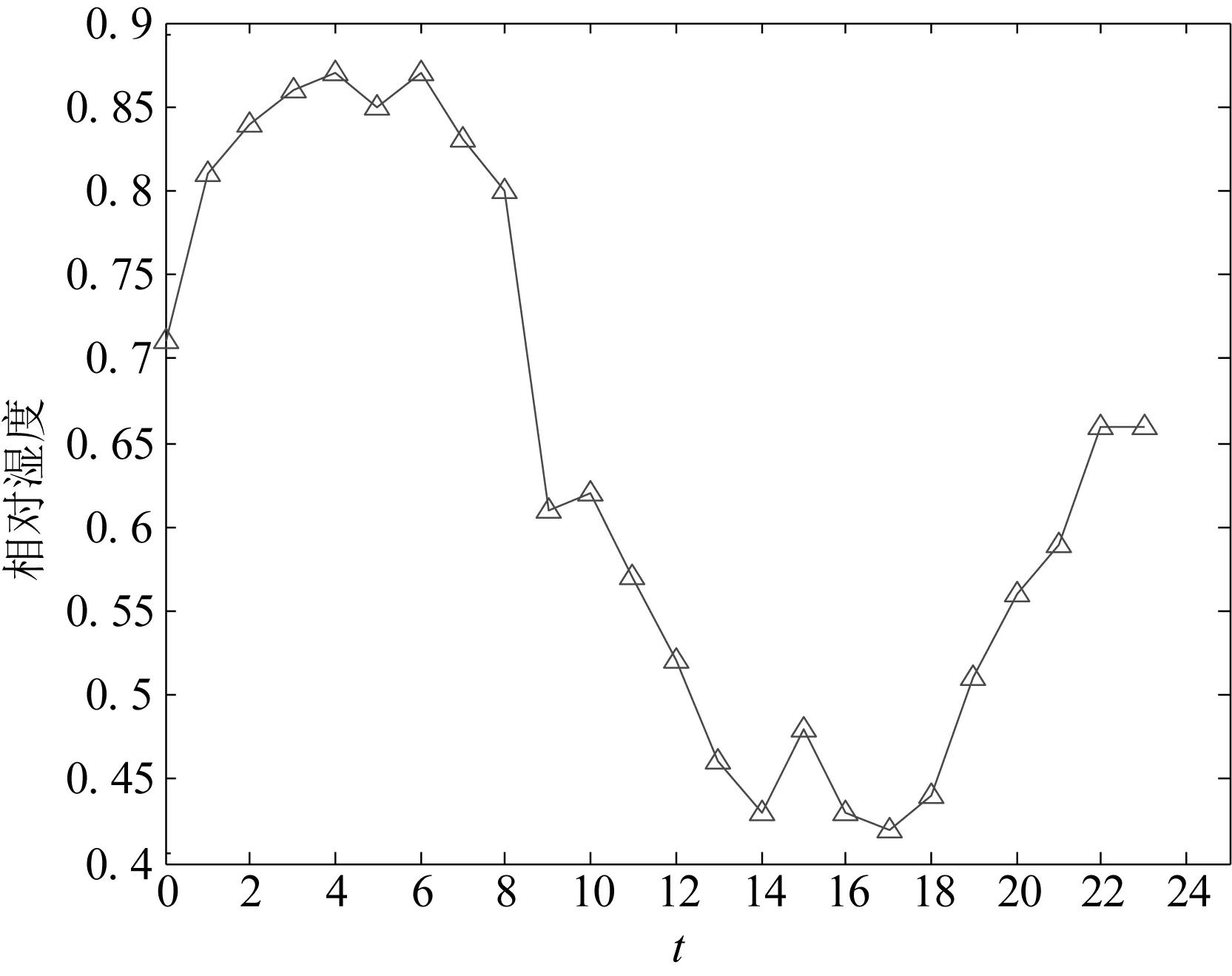
图9 湿度曲线
冷却塔特性参数:该电厂冷却塔淋水面积为5 500m2;塔有效高度:123.4m;塔有出口直径52.544m;淋水填料底部塔内径84.662m;塔进风口面积与进风口上缘面积之比:0.38;特性数Ω=1.69λ0.54。
对于循环水流量不能连续调节的循环水系统,循环水的运行模式的调节应使凝汽器处于最佳真空状态,表2是图9与图10同一天中的环境参数、负荷参数以及出塔水温的预测结果。

表2 出塔水温的预测结果
5结语
本文对传统的遗传算法进行了改进,并将其应用到冷却塔出塔水温的计算中。考虑到理论计算与实际之间会存在误差,本文对适应度函数进行了在线修正,根据当前的进出塔水温和进口风速,实时修正适应度函数,并利用修正后的适应度函数对下一刻的出塔水温进行预测,提高了出塔水温预测的准确性,这对循环水泵的优化具有一定指导意义。
参考文献:
[1]王玮,曾德良,杨婷婷,等.基于凝汽器压力估算法的循环水泵最优运行[J].中国电机工程学报,2010,30(14):7-12.
WANGWei,ZENGDe-liang,YANGTing-ting,etal.Theoptimumrunningofcirculatingwaterpumpsbasedonestimatedcondenserpressure[J].ProceedingsoftheCSEE,2010,30(14):7-12.
[2]葛晓霞,缪国钧,钟澎,等.双压凝汽器循环水系统的优化运行[J].动力工程,2009,29(4):390-393.
GEXiao-xia,MIAOGuo-jun,ZHONGPeng,etal.optimizedoperationofthecirculatingwatersystemwithdual-pressurecondenser[J].PowerEngineering,2009,29(4):390-393.
[3]刘哲,王松岭,王鹏.300MW机组单元制循环水系统优化运行[J].汽轮机技术,2010,52(6):476-477.
LIUZhe,WANGSong-ling,WANGPeng.Optimaloperationofcirculatingwatersystemin300MWunitsystem[J].TurbineTechnology,2010,52(6):476-477.
[4]周兰欣, 蒋波.横向风对湿式冷却塔热力特性影响数值研究[J].汽轮机技术,2009,51(3):165-168.
ZHOULan-xin,JIANGBo.Numericalstudyofcrosswindeffectonwetcoolingtowerthermalperformance[J].TurbineTechnology,2009,51(3):165-168.
[5]赵振国.冷却塔[M].北京:中国水利水电出版社,1997.
[6]闫文周.逆流冷却塔热力计算电算方法的探讨[J].电力建设,1996(1):13-15.
YANWen-zhou.ThermodynanicCalculationMethodforAdverseCurrentCoolingTower[J].ElectricPowerConstruction, 1996(1):13-15.
[7]夏林,刘德有,丁伟.火电机组冷却塔变工况特性研究[J].热能动力工程,2014,29(3):326-332.
XIALin,LIUDe-you,DINGWei.Studyoftheoff-designOperatingConditionCharacteristicsofaCoolingTowerinaThermalDowerGeneratorUnit[J].JouralofEngineeringforThermalEnergyandPower, 2014,29(3):326-332.
[8]李琦芬,宗涛,张志超,等.基于焓差法分析自然通风冷却塔出口水温的影响因素[J].动力工程学报,2012,32(8):634-638.
LIQi-fen,ZONGTao,ZHANGZhi-Chao,etal.AnalysisonFactorsInfluencingOutletWaterTemperatureofNaturalDraftCoolingTowerBasedonEnthalpyDifferenceMethod[J].JournalofChineseSocietyofPowerEngineering, 2012,32(8):634-638.
(本文编辑:赵艳粉)
Prediction of Cooling Tower Outflow Temperature Based on Improved Genetic Algorithm
LI Qi-ben1, ZHOU Ming-hao2, DING Sheng-qi1
(1.SongjiangPowerSupplyCompany,SMEPC,Shanghai200090China;2.ShanghaiMunicipal&TrafficDesignInstituteCo.,Ltd.,Shanghai200090,China)
Abstract:There are two equilibrium equations of Natural Draft Counterflow Wet Cooling Tower established on the basis of Merkel enthalpy potential method. The parameters involved in the equilibrium equation are analyzed, then solution of the outflow temperature is converted to solution of the equations. An improved genetic algorithm is proposed and applied to calculation of the outlet water temperature of the tower. The fitness function is corrected in real time for the online prediction of the tower with better accuracy. It has a certain guiding significance for regulation of circulating water pump.
Key words:cooling tower; tower outflow temperature; genetic algorithm; online prediction
DOI:10.11973/dlyny201603019
作者简介:李启本(1987),男,硕士,工程师,从事继电保护工作。
中图分类号:TK264.1
文献标志码:A
文章编号:2095-1256(2016)03-0343-06
收稿日期:2016-01-23
