码复用差分混沌键控性能分析与同步算法

2016-07-04徐位凯蔡国发

重庆邮电大学学报(自然科学版) 2016年3期

关键词：误码率

张　琳，徐位凯，王　琳，蔡国发，胡　伟

(厦门大学信息科学与技术学院，厦门 361005)

码复用差分混沌键控性能分析与同步算法

张琳，徐位凯，王琳，蔡国发，胡伟

(厦门大学信息科学与技术学院，厦门 361005)

摘要：码复用差分混沌键控(code-shifted differential chaos shift keying，CS-DCSK)是一种具有优良抗多径衰落能力的非相干混沌调制技术，虽然非相干混沌调制技术不需要在接收端恢复混沌载波，但准确的符号同步是保证系统性能的前提。介绍了CS-DCSK系统的结构模型，包括发射机和接收机原理以及CS-DCSK独特的信号帧结构，然后采用高斯近似法(Gaussian approximation, GA)分析了高斯信道和Nakagami-m衰落信道下符号同步误差对CS-DCSK误码性能的影响，最后提出一种符号同步算法，该算法通过发送训练序列首先完成帧间的粗同步，在粗同步的基础上完成帧内的细同步。仿真结果表明，在高斯信道和Nakagami-m衰落信道下，仿真结果与理论分析基本一致。通过与理想同步情况下的误码率性能比较，提出的同步算法存在2 dB左右的性能损失。

关键词：码复用差分混沌键控(CS-DCSK)；非相干接收机；符号同步；高斯近似法；误码率

0引言

混沌键控调制(chaos shift keying，CSK)[1]是以混沌信号为载波，解调时基于混沌信号为参考模板的一种相干调制技术。由于混沌信号的初始敏感性[2]，恢复用于相干解调的模板信号变得不准确，由此产生了差分混沌键控调制(differential chaos shift keying，DCSK)[3]。DCSK是一种传输参考(transmitted reference，TR)技术，一个DCSK符号分为2个时隙，第1个时隙用于传输参考信号，第2个时隙用于传输信息承载信号，当发送信息比特为1时，信息承载信号就是第1个时隙参考信号的复制，当发送信息比特为0时, 信息承载信号就是第1个时隙参考信号的相反信号。由于混沌信号的类随机性，在DCSK系统中传输不同比特的调制符号的能量是不固定的，这会导致系统误码率的不稳定。为了解决该能量估算问题，Kolumban等人提出了频率调制混沌键控(frequency-modulated fifferential chaos shift keying，FM-DCSK)技术[4-6]，该技术解决了能量不固定的问题。但是差分混沌键控调制和频率调制混沌键控都是通过延时电路来实现参考信号和信息承载信号的正交，而在宽带或者超宽带传输时，延时电路实现复杂，增加了系统实现成本。因此，文献[7]提出了基于Walsh码的正交码复用差分混沌键控(code-shifted differential chaos shift keying，CS-DCSK)调制。该方案利用Walsh码实现参考信号和信息承载信号的正交，不同于传统的时隙正交传输参考方案，CS-DCSK调制避免了接收机采用延时电路，因此降低了系统的复杂度。

目前，非相干传输系统的同步算法得到了广泛的关注[8-13]，文献[8]探讨了差分传输参考(differential transmitted reference ，DTR)系统的帧同步问题，该算法主要通过相邻帧脉冲的相关值和一个符号内的帧能量值来实现帧同步。与传统的亚纳秒级精度的算法相比，该方法精度一般，但是具有较低的复杂度和快速收敛的能力。文献[9]研究了传输参考超宽带(transmitted reference ultra wide band，TR-UWB)系统的帧同步问题，该算法主要通过三分之一帧长的滑动窗口收集信号能量，并通过能量峰值等步骤完成帧同步。该算法具有很好的灵活性，当采样频率较低时，也能获得良好的系统性能。文献[10]讨论了频率调制差分混沌键控超宽带(FM-DCSK UWB)系统的同步问题，该算法主要利用混沌序列的相关特性，逐渐减小积分窗口，直到达到预定的门限次数，实现符号同步。除能量检测同步算法外，还有很多同步算法[11-13]，如：码匹配法，最大似然法，脏模板法等。但是这些算法并不适合CS-DCSK系统，这是由于混沌信号的类噪声特性和CS-DCSK独特的码复用结构。本文分析了在给定同步误差条件下CS-DCSK的性能，导出了误码率的闭合表达式，揭示了同步误差与误码率之间的关系，提出了一种简单的基于能量检测的同步算法，该算法利用混沌信号的相关特性和Walsh码的正交特性来完成符号同步。

1系统模型

码复用差分混沌键控调制的发射机和接收机框架如图1所示，第l个符号可表示为

(1)

(1)式中：al∈{-1,+1}是信息比特bl∈{1,0}的映射；WR,K+1和WI,K+1是2个不同的Walsh码序列，分别被用于参考信号和信息承载信号；Nf是Walsh码序列的长度；c(t)是时长为Tf、采样点数为β=Tf×fs的混沌信号，其中fs是采样频率，Tf是帧长；Ts=Nf×Tf是一个符号周期，且定义扩频因子w=Ts×fs=Nfβ。

图1　码复用差分混沌键控系统的结构模型Fig.1　Models of CS-DCSK system

由于Walsh码的正交特性，构建了CS-DCSK独特的码复用结构，当信息比特为0时，符号内奇数帧的信号加倍，偶数帧的信号相互抵消，当信息比特为1时，则与信息比特为0时相反，以4阶CS-DCSK为例，信号帧结构如图2所示。

图2　4阶码复用差分混沌键控信号结构图Fig.2　Structure of 4 order CS-DCSK signal

多径信道表示为[14]

(2)

(2)式中：L是多径数；αl，τl分别是第l径的幅度和时延。经过信道传输后，接收信号可以表示为

(3)

(3)式中：⊗代表卷积运算；n(t)是均值为0，方差为N0/2的高斯白噪声。

2符号同步误差下的性能分析

2.1高斯信道

(4)

(4)式中：E[.]和Var[.]分别是混沌信号的均值和方差。更多的混沌信号发生器，参见文献[15-16]。

由于同步误差的影响，下一个比特将会影响当前比特误码率的判定，以下分4种情况讨论。

当传输的前后信息比特为0-0时，观测信号为

(5)

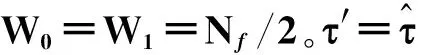
展开(5)式，得到：

(6)

(6)式中各变量的均值分别为

(7)

则观测信号的均值为

(8)

(6)式中各变量的方差分别为

(9)

由于变量之间是互不相关的，它们的协方差为0，则得到观测信号的方差为

(10)

利用高斯近似法，可以得到当传输的前后信息比特为0-0时的误码率为

(11)

当传输的前后信息比特为0-1时，观测信号为

(12)

同理，得到此时的误码率为

(13)

当传输的前后信息比特为1-0时，观测信号为

(14)

同理，得到此时的误码率为

(15)

当传输的前后信息比特为1-1时，观测信号为

(16)

同理，得到此时的误码率为

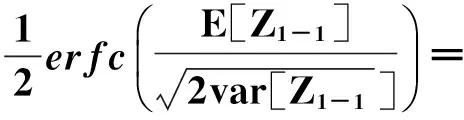
(17)

综上，高斯信道下有同步误差存在时的误码率为

(18)

2.2Nakagami-m信道

当信道参数αi满足Nakagami-m分布时，概率密度函数表示为[17]

(19)

假设mi=mv=m，且有i,v=0,1,…,L-1且i≠v，则γb的分布可用瞬时生成函数(momentgeneratingfunction,MGF)[18]表示为

(20)

当多径信道路径是相互独立的，且信道参数满足Nakagami-m分布时，同步误差下的条件误码率可以近似为[19]

BER(α0,α1,…,αL-1,τ′)≈

(21)

最后，积分得到多径信道下有同步误差存在时的误码率为

(22)

3同步算法

3.1帧间粗同步

图3　基于训练序列的4阶CS-DCSK的同步算法示意图Fig.3　Diagram of the algorithm of 4-order CS-DCSKbased on the training sequences

粗同步就是快速地找到信道时延τ的大致范围。在码复用差分混沌键控调制系统中，在接收端可以得到不同时钟延迟帧的一个符号的能量值，由于码复用差分混沌键控独特的码复用结构，所以接收机时钟以2帧为单位移动，如图3a所示，当信道时延小于2帧时，E0所包含的脉冲能量值比E2所包含的脉冲能量值大，即E0> E2，同理当信道时延大于或者等于2帧时，E2所包含的脉冲能量值比E0所包含的脉冲能量值大，即E0< E2。

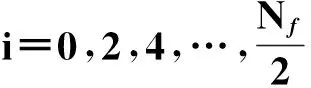
(23)

(23)式中：|(·)|是幅度值；r2(t)是信号的能量。

由(23)式，可以得到延迟不同帧的能量值，当能量值达到最大时，粗同步完成，得到信道时延估计值为

(24)

经过帧间粗同步之后，就可以得到信道时延在一个符号中的位置，缩小了时延估计的搜索范围。

3.2帧内细同步

(25)

当能量S达到最大值时，更新时延估计值，则得到细同步时间为

(26)

4仿真结果

图4　高斯信道下同步误差的影响Fig.4　Effect of synchronization error in AWGN channel

图4表明高斯信道下同步误差的理论分析和仿真基本一致，且当同步误差增大时，系统的误码率恶化，这是由于同步误差的增大，信号能量收集的误差也增大，从而导致解调时误码率恶化。除此之外，当时延为0 ns即完全同步时，信噪比SNR=20 dB时， CS-DCSK系统和DCSK系统几乎重合，表明CS-DCSK和DCSK的系统性能相当，但与DCSK系统相比，CS-DCSK系统对同步误差更敏感即误码恶化速度更快。

图5　Nakagami-m信道下同步误差的影响Fig.5　Effect of synchronization error in Nakagami-m channel

图5表明Nakagami-m信道下同步误差的影响和AWGN信道基本一致，当同步误差增大时，误码率也会恶化，且和DCSK系统相比，CS-DCSK系统对同步误差更敏感。

图6　算法与理想同步的对比Fig.6　Comparison of the perfect synchronizationand synchronization algorithm

图6给出了提出的符号同步算法和理想同步的CS-DCSK系统性能比较，可以看出，与理想同步的CS-DCSK系统相比，本文提出的算法大约有2 dB左右的性能损失。表明该算法有待进一步优化，但是对非相干混沌通信系统的符号同步有一定的借鉴意义。

5结论

本文首先推导了AWGN信道和Nakagami-m信道下，存在符号同步误差的CS-DCSK的误码率表达式，仿真结果验证了理论分析的正确性。其次，与DCSK系统相比，CS-DCSK系统对同步误差更敏感，因此，研究性能良好的同步算法对于CS-DCSK系统具有重要的意义。最后，针对CS-DCSK独特的码复用结构，本文提出了一种基于训练序列的符号同步算法，该算法能快速实现同步，与理想同步的CS-DCSK系统相比，大约有2 dB左右的性能损失。

参考文献：

[1]DEDIEU H, KENNEDY M P, HASLAR M. Chaos shift keying: modulation and demodulation of a chaotic carrier using self-synchronizing Chua’s circuits[J].IEEE Transactions on Circuits and systems II: Analog and digital signal processing, 1993, 40(10): 634-642.

[2]STROGATZ S H. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering[M]. Boulder: Westview press, 2014.

[3]KOLUMBAN G, VIZVARI B, SCHWARZ W, et al. Differential chaos shift keying: A robust coding for chaos communication[C]//Proc. NDES’96. Oakland： IEEE Press, 1996: 87-92.

[4]KOLUMBAN G, KIS G, KENNEDY M P, et al. FM-DCSK: A new and robust solution to chaos communications [C]// Proceedings of the NOLTA. Hawaii： IEEE Press, 1997，97: 117-120.

[5]WANG Lin, MIN Xin, CHEN Guangrong. Performance of SIMO FM-DCSK UWB system based on chaotic pulse cluster signals[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2011, 58(9): 2259-2268.

[6]ZHANG Chaoxian, WANG Lin, CHEN Guangrong. Promising Performance of PA-Coded SIMO FM-DCSK Communication Systems[J]. Circuits, Systems & Signal Processing, 2008, 27(6): 915-926.

[7]XU Weikai, WANG Lin, KOLUMBAN G. A new data rate adaption communications scheme for code-shifted differential chaos shift keying modulation[J]. International Journal of Bifurcation and Chaos, 2012, 22(8): 1250201.

[8]NIE Miao, ZHANG Zhongzhao. Fast and Low-Complexity Frame-Level Synchronization for Differential Transmitted Reference Receivers [C]//Information Engineering(ICIE), 2010 WASE International Conference on IEEE. Beidaihe, Hebei: IEEE Press, 2010: 94-97.

[9]NGUYEN H V, TRAN M H. Synchronization algorithm and PFGA implementation for Transmit-Reference UWB receiver [C]//Communications and Electronics, 2012 Fourth International Conference on IEEE. Hue：IEEE Press, 2012: 506-511.

[10] CHEN Shaoyuan, WANG Lin, CHEN Guangrong. Data-aided timing synchronization for FM-DCSK UWB communication systems[J]. IEEE Transactions on Industrial Electronics, 2010, 57(5): 1538-1545.

[11] YING Yeqiu, GHOGHO M, SWAMI A. Code-assisted synchronization for UWB-IR systems: Algorithms and analysis[J]. IEEE Transactions on Signal Processing, 2008, 56(10): 5169-5180.

[12] TIAN Zhi, LOTTICI V. Low-complexity ML timing acquisition for UWB communications in dense multipath channels[J]. IEEE Transactions on Wireless Communications, 2005, 4(6): 3031-3038.

[13] YANG Liuqing, GIANNAKISG B. Blind UWB timing with a dirty template[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing, 2004. Proceedings.(ICASSP’04). Motreal：IEEE Press, 2004: 509-512.

[14] KARAGIANNIDIS G K, SAGIAS N C, MATHIOPOULOS P T. The N* Nakagami fading channel model[C]// International Symposium on Wireless Communication Systems. Siena： IEEE Press, 2005: 185-189.

[15] LAU F C M, TSE C K. Chaos-based digital communication systems[M]. New York: Springer, 2003.

[16] YU Lei, BARBOT J P, ZHENG Gang, et al. Compressive sensing with chaotic sequence[J]. IEEE Signal Processing Letters, 2010, 17(8): 731-734.

[17] WICKER S B. Error control systems for digital communication and storage[M]. Englewood Cliffs: Prentice hall, 1995.

[18] SIMON M K, ALOUINI M S. Digital communication over fading channels[M]. John Wiley & Sons, 2005.

[19] XIA Yongxiang, TSE C K, LAU F C M. Performance of differential chaos-shift-keying digital communication systems over a multipath fading channel with delay spread[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2004, 51(12): 680-684.

Performance analysis and synchronization algorithmfor CS-DCSK system

ZHANG Lin, XU Weikai, WANG Lin, CAI guofa, HU wei

(School of Information Science and Engineering, Xiamen University, Xiamen 36100, P.R.China)

Abstract:Code-shifted differential chaos shift keying (CS-DCSK) is a non-coherent chaotic demodulation technology that has low complexity and good performance of anti-multipath fading channels. It does not require recover chaos carrier at receiver, but the accurate symbol synchronization is the prerequisite to guarantee the performance of the system. This paper firstly introduces the structure of CS-DCSK system including transmitter, receiver and the unique signal frames of CS-DCSK. Then it investigates BER performance of CS-DCSK with synchronization error in AWGN and Nakagami-m channel respectively using gaussian approximation (GA) method. At last, an efficient synchronization algorithm is proposed for CS-DCSK. In the algorithm, firstly we use training symbols to complete inter-frame coarse timing, then to finish fine timing on the basis of the coarse timing. Simulation results show that the simulation and the theoretical analysis are basically consistent with both AWGN and Nakagami-m channels. Compared with the perfect synchronization, the BER performance of the proposed synchronization algorithm has about 2dB performance loss.

Keywords：code-shifted differential chaos shift keying(CS-DCSK); non-coherent receivers; symbol synchronization; Gaussian approximation (GA) method; BER

DOI：10.3979/j.issn.1673-825X.2016.03.008

收稿日期：2015-12-13

修订日期：2016-03-31通讯作者：徐位凯xweikai@xmu.edu.cn

基金项目：国家自然科学基金(61001073)

Foundation Item：The National Natural Science Foundation of China(61001073)

中图分类号：TN929.5

文献标志码：A

文章编号：1673-825X(2016)03-0330-07

作者简介：