基于FPGA的微弱信号检测与实现技术

2016-07-04高振斌田晓旭

重庆邮电大学学报(自然科学版) 2016年3期

高振斌，田晓旭

(河北工业大学电子信息工程学院，天津 300401)

基于FPGA的微弱信号检测与实现技术

高振斌，田晓旭

(河北工业大学电子信息工程学院，天津 300401)

摘要：研究了杜芬混沌振子(Duffing chaos oscillator)微弱信号检测算法及其现场可编程门阵列(field programmable gate arrays，FPGA)实现技术。根据杜芬系统在混沌和大周期2种状态下相图的明显区别，运用基于相图分割的信号检测方法，在FPGA上实现了杜芬混沌算法与系统状态判别方法的结合。根据并行运算与流水线原理，对杜芬方程的结构进行调整。采用递推数列的方法计算正弦值，以便节约存储空间。使用VHDL硬件语言设计了杜芬阵子系统中核心的四阶龙格库塔(fourth order Runge Kutta algorithm,RK4)模块和状态检测模块，在vivado集成开发环境下仿真验证了设计的正确性。通过改变策动力的频率，系统可以检测各种频率的微弱正弦信号。经判断，该系统可实现对与系统信号同频率信号的检测。

关键词：微弱信号检测；现场可编程门阵列(FPGA)；杜芬混沌阵子；递推数列

0引言

微弱信号检测技术在通讯、雷达、声纳、地震、工业测量、机械系统实时监控等领域应用广泛[1-3]。Duffing振子是一种典型的混沌振子，对周期信号极其敏感，而对噪声具有一定的免疫力，因此，被广泛应用于微弱信号检测[4-5]。自1992年R.Brown等首次提出了运用Duffing振子检测周期信号以来，利用Duffing振子进行信号检测的理论不断得到改进和发展[4-7]。王冠宇等[5]研究了Duffing振子在强噪声背景中进行信号检测的原理及可行性；夏均忠等[6]对淹没在噪声中的汽车微弱振子信号做了识别研究；曾孝文等[7]利用数字信号处理(digital signal processing, DSP)技术和混沌理论对水下微弱信号进行了检测，具有一定的成果。上述研究成果分别从理论论证、仿真验证等方面对Duffing振子微弱信号检测进行了研究，为工程实现提供了依据。

传统的Duffing振子微弱信号检测大多都是电路实现方法的理论研究。现运用现场可编程门阵列(field programmable gate arrays，FPGA)技术对Duffing系统进行实现，该技术适合对数字信号进行处理。

1检测方法

1.1混沌振子信号检测原理

Duffing方程形式为[8]

(1)

Duffing阵子相轨迹特征为在k固定的情况下，系统状态随策动力系数γ的变化出现有规律的变化，γ从0逐渐增加时，相轨迹由周期内轨运动状态转变为混沌运动状态。当γ继续增加到由混沌转向大周期的临界值时，系统相轨迹由混沌运动状态转变为大周期运动状态[8]。

根据这个特点，可以得到检测正弦信号的原理：把γ设为略小于由混沌转向大周期的临界值，使系统处于混沌与大周期的临界状态，将待测正弦信号输入系统，如果系统由混沌状态变为大周期状态，就说明待测信号中包含与策动力信号频率相同的正弦信号。否则，不包含与策动力信号频率相同的正弦信号。

1.2杜芬方程的数值解法

四阶龙格库塔法(fourthorderRungeKuttaalgorithm，RK4)是一种在已知系统初值和状态方程导数的条件下求解常微分方程的显示迭代法，具有比欧拉法更高的计算精度，非常适合用于对输出结果要求高的工程中[8]。

已知Duffing离散化方程为

(2)

(2)式中：阻尼比k=0.5；ω为系统余弦信号角频率；h为步长；i=0,1,…,n。

RK4解常微分方程主要是基于迭代。由给定的初值(xi,yi)和状态方程先求出斜率系数k，进而算出下一样本点(xi+1,yi+1)的值，以此为基础进行迭代计算，如(3)式和(4)式。

(3)

对hkx，hky的求解是迭代过程，其计算过程为

(4)

(4)式中，i=1,2,3,4。

根据RK4求解离散化的Duffing方程[8]，所求结果为(3)式。(3)式为混沌振子求解的依据。

1.3系统状态判定方法

对系统状态的判决是微弱信号检测的关键。由混沌系统信号检测原理可知，在有不同信号输入时，系统会处于不同状态。通过对系统不同状态的判定，才能检测是否有待测信号输入[9]。

本文利用内接矩形法来对混沌系统状态进行判决。其基本原理是根据杜芬阵子系统在混沌状态和大周期状态时相轨迹具有明显差别，在Duffing振子的相图中做一封闭区域[9]，在大周期状态下轨迹点主要集中在区域外，混沌状态下轨迹点更多地集中在区域内，通过统计相轨迹点处于区域外的数量，就可以判定系统状态，其原理图如图1所示。

根据以上原理，检测正弦信号的方法：首先，调节γ使系统处于混沌和大周期的临界状态；然后，修改系统频率使ω按一定步长搜索，当ω接近输入信号的角频率ωi时，系统由混沌变为大周期状态，此时区域外点数所占比例最大，这样就可以检测出待测信号的频率。文献[9]对信号检测性能进行了分析，其结果为内接矩形法能用于信噪比大于-30dB时的信号检测。在信噪比更低时，检测性能逐渐变差，但通过概率分布仍可以推断出输入中可能含有某频率分量的信号[9]。

图1　内接矩形法实现原理图Fig.1　Schematic diagram of inscribed rectangle method

2方案及实现

2.1整体结构

根据上文分析，主要计算有余弦值、乘法、系数求和等过程。得到Duffing系统整体结构如图2所示，首先运用余弦计算模块求出余弦值，再将余弦结果输入到迭代计算模块，求出结果，并将每次的计算输出结果送入判决模块。

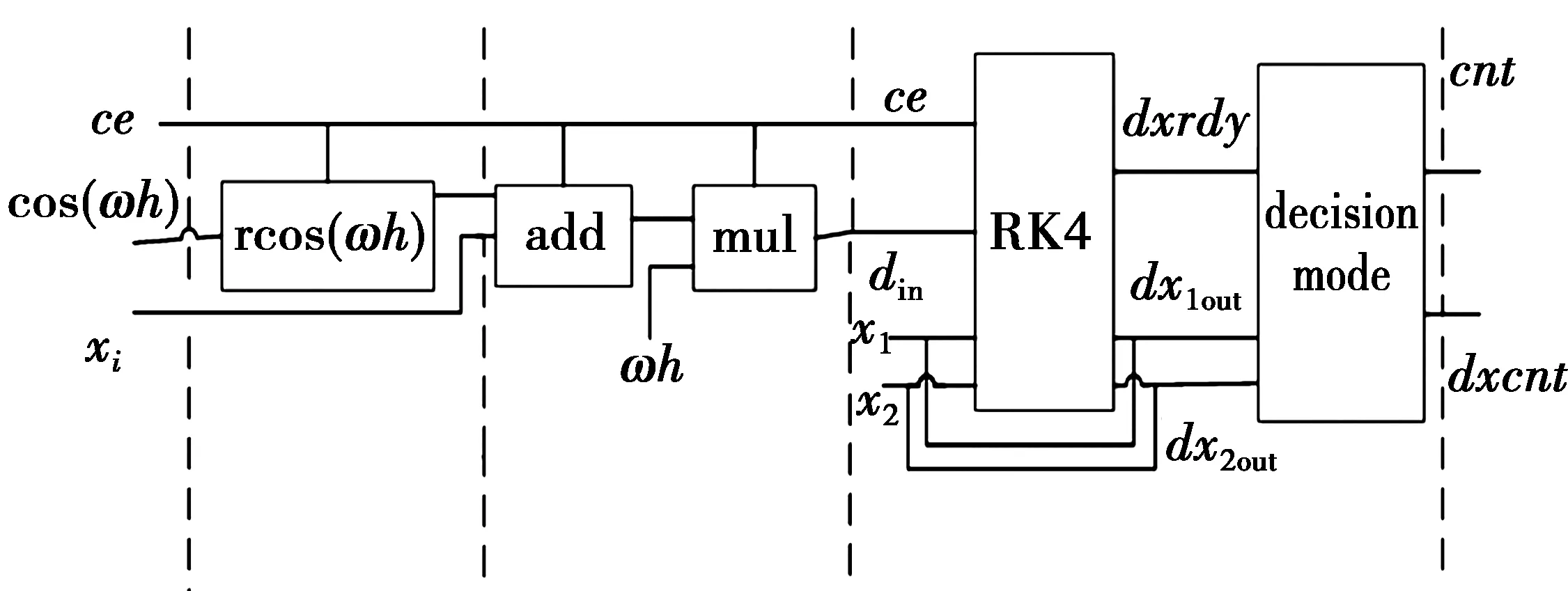
图2　Duffing系统整体结构Fig.2　Overall structure of Duffing system

2.2余弦值计算模块的实现

根据Duffing方程求解公式可知，在方程计算时需得到离散余弦值cos(ω0hi)，其中，i=1,2,…,n。通常在硬件实现过程中采用查表法得到余弦值，本文利用递推方法计算，与查表法相比，只需存储初始相位及其余弦值，避免了每次计算的查表过程，并节约了大量存储空间。

假设x=ω0h，根据三角公式，得到余弦值的递推公式为

cos[i(ω0h)]=2cos(ω0h)cos[(i-1)(ω0h)]-

cos[(i-2)(ω0h)]

(5)

本设计在计算余弦值时把ω0h当作整体，存储cos(ω0h)的值，再递推得到cos(iω0h)，所以，该计算方法所需要的工作为1次乘法，1次加法，2次变量复制。其在FPGA上实现的硬件结构如图3所示。

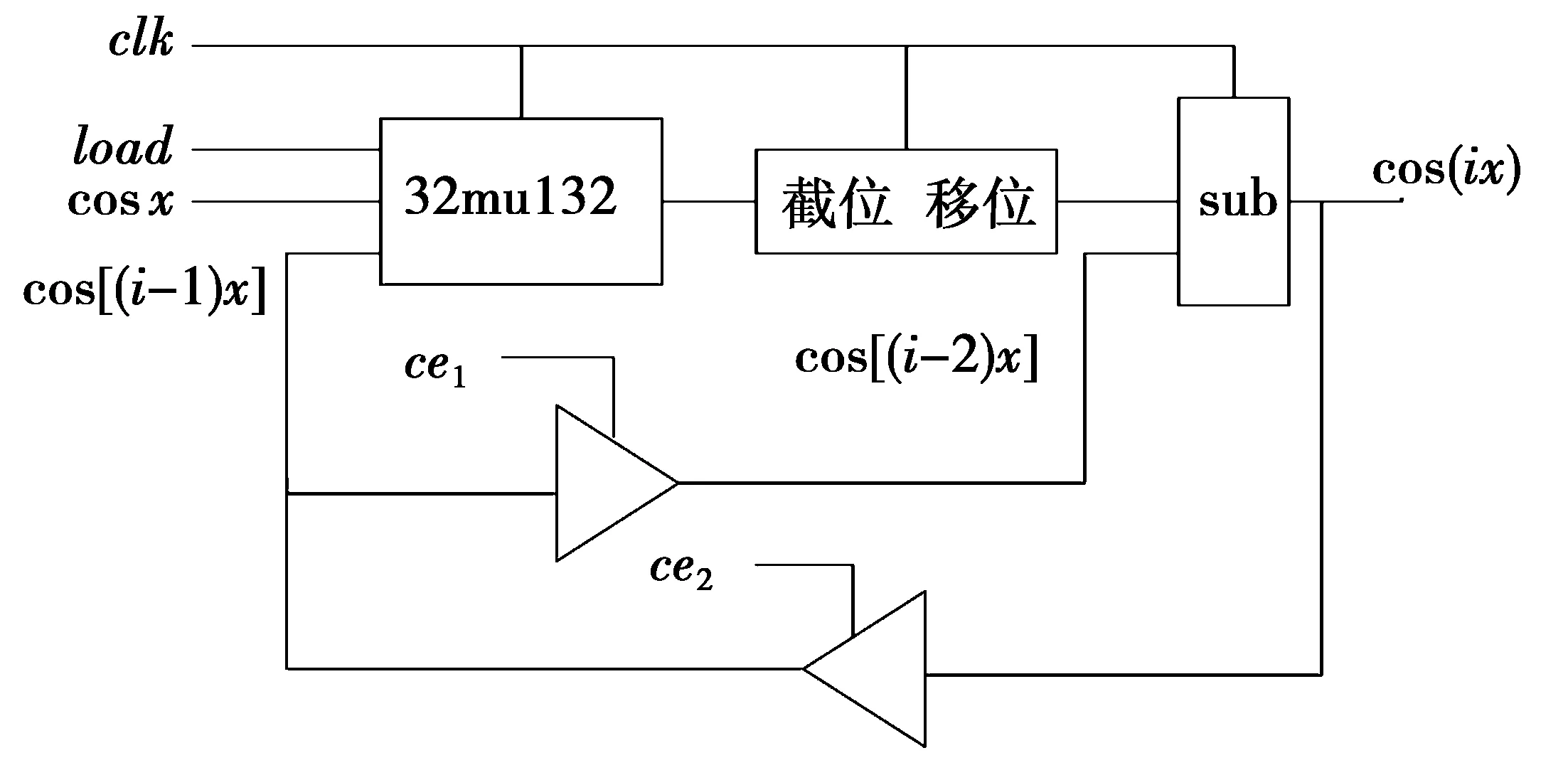
图3　cos(ix)模块硬件实现框图Fig.3　Implementation block diagram

用vivado进行仿真，结果如图4所示。由图4可以看出，该方法在FPGA上能实现平滑的正弦波。

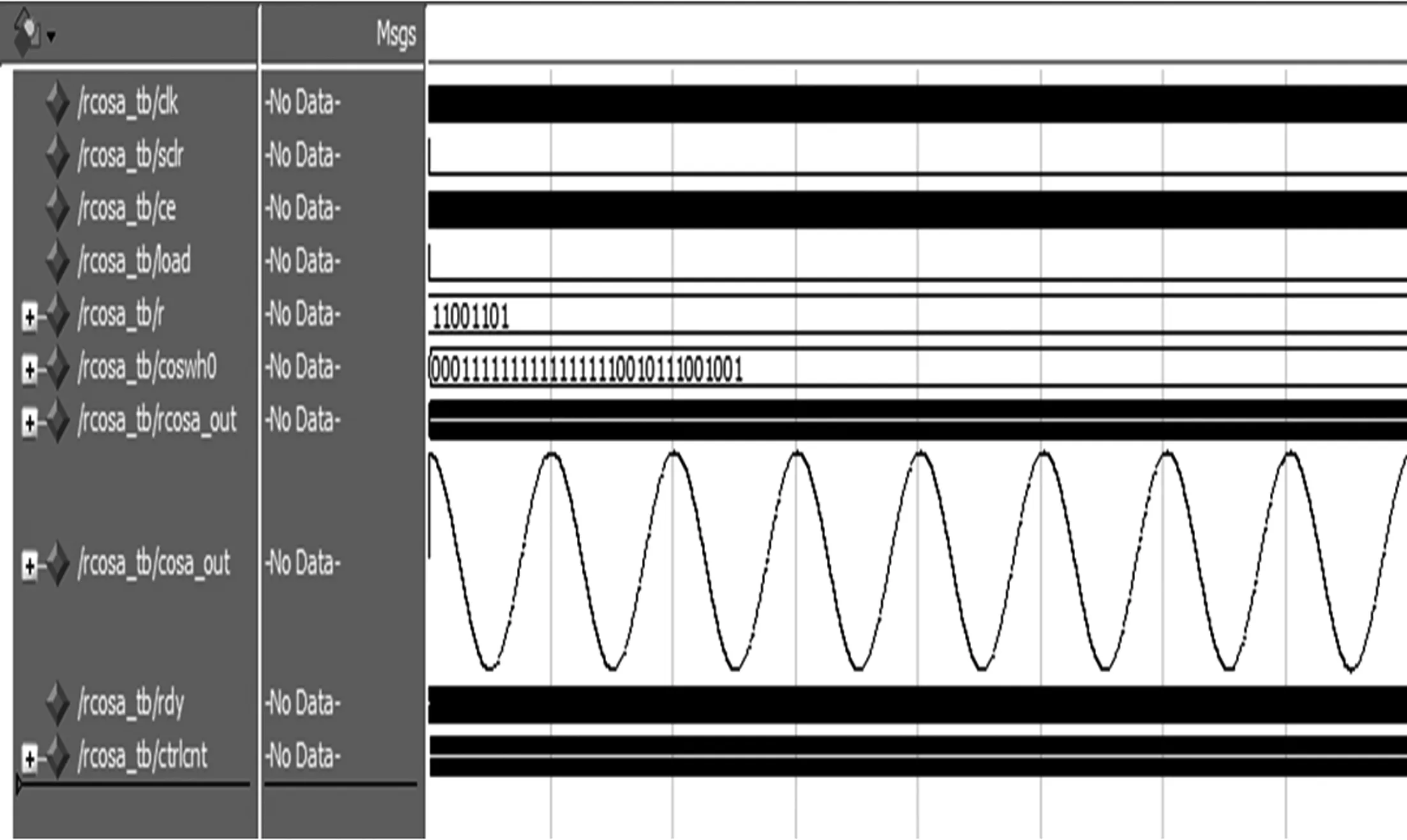
图4　cos(ix)仿真结果Fig.4　Simulation result of cos(ix) module

2.3迭代模块的实现

在设计RK4模块时需要将微分方程的具体步骤与FPGA并行运算相结合，即在程序设计时不按公式顺序计算，而是从硬件角度出发，对运算模块进行有效分配。根据这种思想，可以实现模块共用，从而避免一些硬件资源的浪费。通过并行运算及流水线作业，可以节省运行时间，提高计算速度。

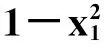
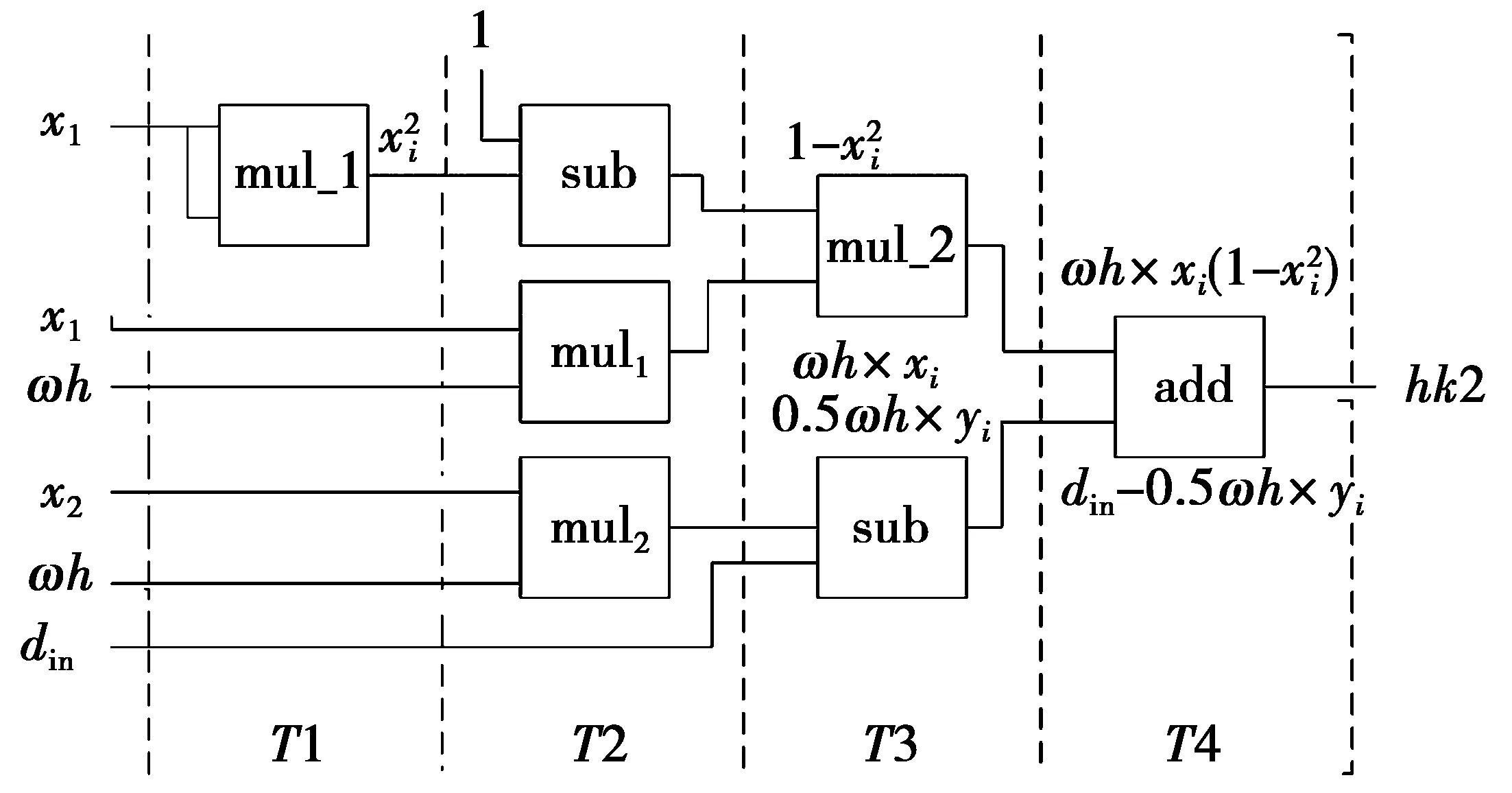
图5　RK4法解Duffing方程乘法器分配Fig.5　Solving Duffing equation with RK4

由(4)式，用RK4解杜芬方程是顺序迭代过程，其流程图如图6所示。首先实现对hk1,hk2,hk3和hk4求解，然后运用累加器对hk1,hk2,hk3和hk4的值进行累加。整个计算过程由5位计数器输出的高3位控制，creg是5位二进制寄存器，用于存储计数器的计数值；c是3位二进制寄存器，用于存储计数器的高3位计数值，其中，计数器是二十进制计数器，在时钟上升沿时加1。整个过程需要20个时钟周期，其硬件结构图如图7所示。

图6　RK4法解Duffing方程状态流程图Fig.6　Flow chart of solving Duffing equation with RK4

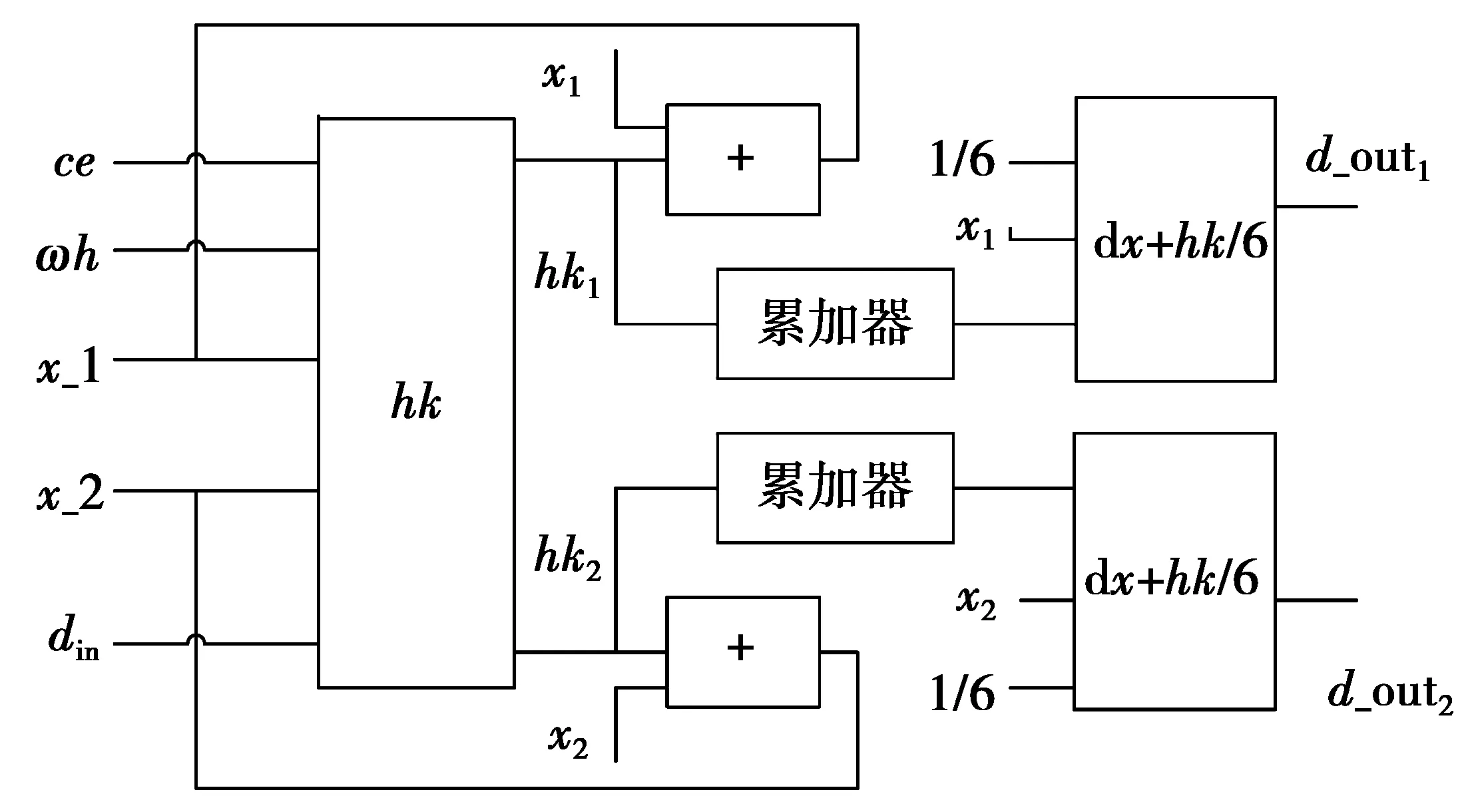
图7　RK4法解Duffing方程硬件结构图Fig.7　Structure diagram of solving Duffing equation with RK4

2.4状态判别电路

如前文所述，内接矩形法的实现流程图如图8所示。由原理可知，该模块需要1个比较器、1个计数器和1个除法器，为了减少运算可将数据总数设为定值，只需对矩形外点数进行统计，这样就免去了除法器的使用，过程简单，适合在FPGA上实现。具体过程：将各个角频率下所需计算的数据总数设为定值216，由计数器控制cnt为计数器的计数值；dxcnt表示矩形外点数；ωout表示计数值最大时所对应的角频率；cntmax用于存储计数最大值。首先，对系统初始化，将cnt和dxcnt清0，给系统角频率ω赋初始值ω0，ωout赋初始值ω0，令cntmax=0；然后，将数据输入系统中进行计算，在计算过程中，每完成一次迭代的计算，对cnt加1，并判断所计算出的结果是否满足在矩形外，若满足，则对dxcnt加1，然后，进行下一次迭代的计算。在每次计算时，都要判断cnt的值是否为 216，如果cnt等于216，就更新ωout和cntmax的值，然后将cnt和dxcnt清零，给角频率加一个步长值，进行下一系统角频率的计算。其硬件结构图如图9所示。根据上述理论，检测某频率的待测信号时，只需对各个频率值进行扫描，并分别统计各频率时状态判决电路输出的计数值，计数值最大的值所对应的频率就是待测信号的频率。

3实现结果及分析

3.1数的表示方法

本设计采用VHDL语言进行定点程序编程，根据计算中变量的动态范围将数据定为32位的定点小数格式，包括1位符号位、2位整数位和29位小数位。用h表示角频率搜索的步长，一般情况下，角频率ω相对较大，而步长h相对较小，若分别用32位的定点小数表示，则ω会产生溢出，且h表示也不精确，而ω和h相乘的结果在32位定点小数表示的范围内，因此，本论文把ω和h相乘的结果当作一个整体作为系统的输入，这样就可以避免数据的溢出，同时减少数据表示的位数，从而节省了部分硬件资源。

图8　内接矩形法实现流程图Fig.8　Flow chart of inscribed rectangle method

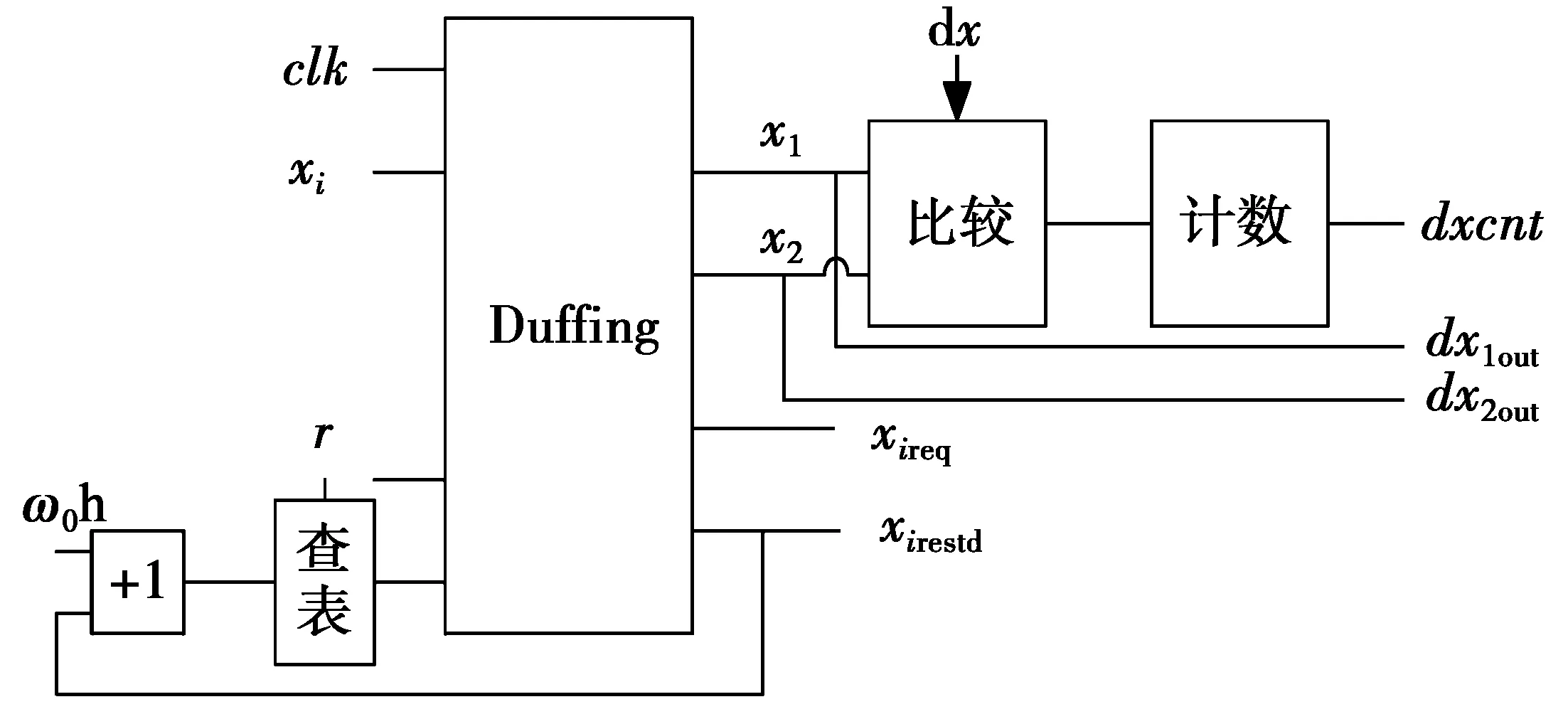
图9　内接矩形法硬件图Fig.9　Structure diagram of inscribed rectangle method

3.2实现结果

3.2.1零输入时的结果

在输入为0的情况下，改变γ的值，使系统分别处于不同的状态，观察其输出结果。图10为γ=0.75时的结果；图11为γ=0.875时的结果。从图10和图11可以看出，当γ=0.75时，系统处于混沌状态，输出结果杂乱无章；当γ=0.875时，系统处于大周期状态，输出结果有一定规律。该结果与上文所述原理一致。

3.2.2状态判决电路的判决结果

图12为状态判决电路的输出结果，检测出的频率与输入的待测信号的频率相同，其中，ω0hout为被检测出的信号频率的定点值。

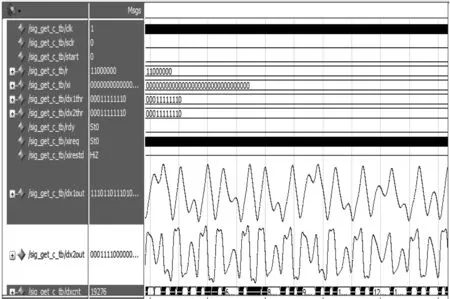
图10　γ=0.75混沌状态输出Fig.10　Output of chaotic state

图11　γ=0.875大周期状态输出Fig.11　Output of periodic state

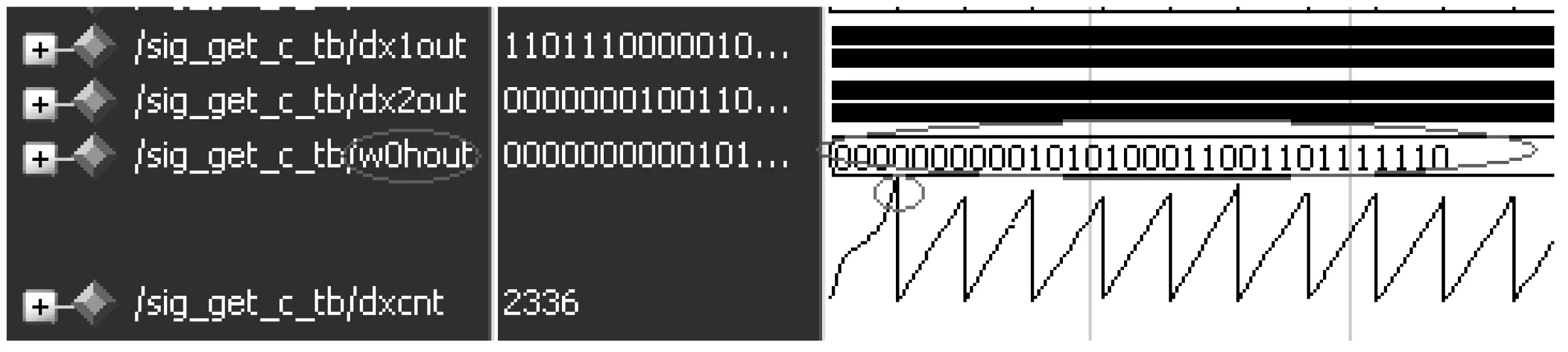
图12　状态判决电路输出结果Fig.12　Output of state-decision circuit

3.2.3资源分析与性能分析

对设计进行功耗分析，如图13所示，所采用的芯片是Zynq-7000。由图13可知，芯片总功率为0.157 W。对其进行动态分析，片上功率占总功率的23%，占用资源较少。

图13　功耗和资源分析Fig.13　Analysis of power consumption and resources

对设计进行时序分析，首先，对时钟进行约束，然后，观察系统支持的最快时钟。时序分析结果如图14所示。从图14可以看出，建立和保持时间分别为4.532 ns和0.226 ns，脉冲宽度为4.500 ns。由此得到，时钟最高频率为222 MHz。由上文可知，计算一个数据需要20个时钟周期，由此得出，数据吞吐率为11.1 MHz。

图14　时序分析结果Fig.14　Display of time series analysis

4结束语

本论文主要运用FPGA技术实现Duffing系统，根据并发运行原理提高运行速度，利用模块共用节省硬件资源。过程中采用递推数列的方法计算正弦值，在不影响运行速度的前提下减少了硬件资源的利用。此外，本论文还运用相位分割法进行Duffing系统状态的检测并进行仿真，结果正确。

参考文献：

[1]王永生,姜文志,赵建军,等. 一种Duffing弱信号检测新方法及仿真研究[J]. 物理学报,2008(4):2053-2059.

WANG Y S, JIANG W Z, ZHAO J J,et al. A new method of Duffing weak signal detection and simulation research [J].Acta Phys Sin，2008(4)：2053-2059.

[2]翟笃庆, 刘崇新, 刘尧,等. 利用阵发混沌现象测定未知信号参数[J]. 物理学报, 2010, 59(2):816-825.

ZHAI D Q, LIU C X, LIU Y,et al. Use the array chaos phenomenon determination of unknown signal parameters[J]. Acta Phys Sin，2010，59(2)：816-825.

[3]刘海波,吴德伟,戴传金,等. 基于Duffing振子的弱正弦信号检测方法研究[J].电子学报,2013, 01,41(1):8-12.

LIU Haibo, WU Dewei, DAI Chuanjin,et al. A new weak sinusoidal signal detection method based on doffing oscillators[J].Acta Electronica Sinica, 2013, 01,41(1): 8-12.

[4]李月,杨宝骏.混沌振子检测引论[M].北京：电子工业出版社，2004.

LI Yue, YANG Baojun.An introduction to the chaotic oscillator detection[M].BeiJing:Publishing House of Electronics Industry, 2004.

[5]王冠宇, 陈大军, 林建亚,等. Duffing振子微弱信号检测方法的统计特性研究[J].电子学报, 1998, 26(10): 38-44.

WANG Guanyu, CHEN Dajun, LIN Jianya, et al. The statistical characteristics of weak signal detection based on Duffing oscillator[J].Acta Electronica Sinica,1998, 26(10) : 38-44.

[6]夏均忠,刘远宏,冷永刚,等. 微弱信号检测方法的现状分析[J]. 噪声与振动控制,2011,31(3):156-161

XIA Junzhong, LIU Yuanhong, LENG Yonggang,et al. Analysis of method of weak signal detection[J].NOISE AND VIBRATION CONTROL,2011,31(3): 156-161.

[7]曾孝文,唐劲松,姜可宇,等. 利用DSP和混沌理论检测水下微弱信号[J]. 微计算机信息,2008,24(29):167-168，175

ZENG Xiaowen, TANG Jinsong, JIANG Keyu, et al. Using DSP and chaos theory to detect mine weak signals [J]. Microcomputer information,2008, 24(29):167-168，175

[8]高振斌,刘晓哲,郑娜.Duffing混沌振子微弱信号检测方法研究[J].重庆邮电大学学报：自然科学版,2013,25(4):440-444.

GAO Zhenbin, LIU Xiaozhe, ZHENG Na.Study on the method of chaotic oscillator in weak signal detection[J]. Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition，2013，25(4)：440-444.

[9]高振斌,孙月明,李景春. 基于相图分割的Duffing混沌系统状态判定方法[J]. 河北工业大学学报,2015(01):23-27.

GAO Zhenbin, SUN Yueming, LI Jingchun. A method for doffing chaotic system status identification based on phase diagrams segmention [J]. Journal of Hebei University of Technology, 2015(01):23-27.

Weak signal monitoring algorithm and realization technology on the FPGA

GAO Zhenbin，TIAN Xiaoxu

(School of Electronic Information Engineering, Hebei University of Technology, Tianjin 300401,P.R.China)

Abstract:The algorithm of detecting weak signal based on chaotic oscillator theory is researched and implemented in field programmable gate arrays(FPGA). Considering the obvious differences of phase diagram between two conditions of chaos and large cycle, the method based on the phase diagram segmentation is proposed and implemented in FPGA. Duffing chaotic algorithm and system state identification are combined in FPGA. According to the principle of parallel and pipeline, the structure of duffing equation is adjusted. Furthermore, the recursive sequence is applied to calculate sine value for more efficient hardware resource usage. The VHDL hardware description language is employed to design the RK4 module and inspection module which is the core of Duffing system, and verify the correctness of the design on vivado integrated development environment. The system can detect weak sinusoidal signals with various frequencies by changing the frequency of the driving force. Experiments show that the system can detect the signal which has the same frequency with the system signal.

Keywords：weak signal monitoring; field programmable gate arrays(FPGA); chaos oscillator; Duffing chaos oscillator; recursion sequence

DOI：10.3979/j.issn.1673-825X.2016.03.003

收稿日期：2015-07-04

修订日期：2016-03-03通讯作者：高振斌gaozhenbin@hebut.edu.cn

基金项目：国家自然科学基金(61139001)

Foundation Item：The National Natural Science Foundation of China (61139001)

中图分类号：TN911.72

文献标志码：A

文章编号：1673-825X(2016)03-0297-06

作者简介：