基于模糊聚类的实用系数分析方法*

欧阳森　吴裕生　冯天瑞

(华南理工大学 电力学院∥广东省绿色能源技术重点实验室， 广东 广州 510640)

基于模糊聚类的实用系数分析方法*

欧阳森吴裕生冯天瑞

(华南理工大学 电力学院∥广东省绿色能源技术重点实验室， 广东 广州 510640)

摘要:实用系数常用于指导业扩报装时配变容量的选取.文中针对当前实用系数选取时灵活性差、受样本数据影响较大、没有考虑负荷发展特性等问题，设计了一种基于模糊聚类的实用系数分析方法.首先，将用电用户划分为商业、住宅、工业等类型，并建立相应的用电用户的评价指标体系，该体系选取负荷密度、年用电量增长率、配变投运时间3个评价指标来分别描述用电用户的用电水平、变化情况以及负荷发展特性；然后，设计了基于模糊聚类的实用系数等级划分方法，该方法根据3个评价指标进行模糊聚类，划分出实用系数等级，并确定各等级的评价指标及实用系数的中心值；最后，根据待测用电用户的评价指标值与各等级中心值的加权距离和，求得实用系数等级及相应的实用系数值.通过实例分析，验证了该方法的有效性和实用性.

关键词：实用系数；模糊聚类；中心值；业扩报装

业扩报装是供电企业营销和配网管理的一项重要工作[1- 2].近年来，随着社会经济发展，用户用电需求量越来越大，业扩报装容量偏大、设备利用率低、电网的投资过高的问题越来越突出[3].因此，合理选择评估指标，指导业扩报装时配变容量的选取，对提高设备的利用率、配网经济性和可靠性均有重要意义.

对于国内供电企业而言，业扩报装时通常只考虑报装的容量能否满足用电量需求以及是否会影响电网的电能质量，对于反映电网的经济性指标(如设备利用率)并没有特别关注，造成现阶段电网设备利用率较低、用户报装容量偏大等问题.国外供电企业在选择变压器容量时，也是优先考虑满足负荷需求，同时考虑了变压器的损耗、变压器运行维修、网损等带来的费用，但同样也存在着变压器选择容量偏大的问题[4- 5].目前，国内已有部分供电企业采用实用系数来指导业扩报装时配变容量的选取.实用系数是指年最大有功负荷与变压器容量的比值，用来反映用电用户对变压器的使用效率.但现阶段由于缺乏对实用系数的研究，大部分供电企业只能依靠技术人员的经验或采用统一的标准值来选取.这种做法的局限性主要有：①选取过程中主观性太强，过于依赖经验，而且不同技术人员会得出不同的结果；②每一类用电用户只有一个标准值，实用系数类型划分不够细致；③忽略了负荷的发展特性，没有考虑到负荷发展对于实用系数的影响.同一类用户，刚建好的、发展几年的、发展十几年的都具有不同的实用系数，其变化趋势可能是衰减也可能是增长，并且周期也不同，决不能仅用一个值来表征.

目前，国内外关于实用系数的研究屈指可数.业扩报装时多数根据负荷密度来选择配变容量[6]，并没有引入实用系数来考虑配变的利用效率.此外，在现有的研究中，模糊聚类也仅仅应用于负荷密度的选取[7- 10]，在实用系数的选取方面几乎没有.国外关于负荷密度指标选取的研究较少，在选择配变容量时通常通过直接预测总负荷需求量，或者预测用户的土地使用类型的变化来确定，也有少量文献采用模糊理论来确定负荷总量或者土地的类型[11- 12]，但没有关于实用系数方面的研究.国内对于负荷密度的研究较多，近年来有不少学者尝试将模糊理论应用到负荷密度指标的选取中.文献[13]中引入了C均值算法将各类用地性质负荷聚类成不同等级，并采用LS-SVM和遗传算法来预测各地块的负荷密度指标.文献[14]中采用基于熵权的多指标灰靶决策进行预测，并利用类内相似度法进行修正，将模糊数和多指标灰靶决策理论结合起来.文献[15]中通过划分供电区域生成元胞，根据元胞属性进行多级聚类分析，并建立元胞属性和元胞负荷之间的映射关系，来求取负荷密度指标.从文献[13- 15]可以看出，实用系数的求解方法与负荷密度相似，应用模糊聚类方法分析实用系数的方法具有有效性和实用性.这些文献从用户的整体用电水平、建筑面积等角度出发选取负荷密度，但都没有考虑到负荷的发展特性，认为不同发展阶段的用电用户都具有相同的实用系数.

文中以模糊聚类理论为基础，首先将用电用户划分为商业、工业、住宅、办公、文化娱乐、公共设施6个类型[16]，并建立用电用户的评价指标体系；然后，对每一类型，根据评价指标对用电用户进行聚类，得到用电用户的实用系数等级，并确定各等级的评价指标及实用系数的中心值；最后，根据用电用户的评价指标值与各等级中心值的加权距离和，确定待测用电用户的实用系数等级以及相应的实用系数值.该方法除了能够合理地划分各类用电用户的实用系数等级之外，还能根据用户的评价指标进一步地求解出相应的实用系数，有效地改善实用系数选取时的灵活性和可靠性；同时，在采用现有评价指标负荷密度的基础上，引入配变投运年限来体现负荷不同的发展阶段，充分考虑负荷的发展对实用系数的影响，使得计算结果更加可靠.

1用电用户评价指标体系

考虑到用电用户信息的完整性还有待提高，评价指标需要涵盖用电用户多方面的特征.因此，文中选取的评价指标包括负荷密度(X1)、年用电量增长率(X2)、配变投运时间(X3).

对上述3种评价指标的具体分析如下.

(1)负荷密度(X1)

负荷密度是现阶段用来测算用电量和指导变压器容量选取的重要指标，表示某个地区(用户)单位面积的负荷大小.负荷密度计算公式如下：

(1)

式中，P为用电用户的年度用电量，S为用电用户的建筑面积.负荷密度用来权衡一个地区(用户)整体的用电水平.相同建筑面积下，负荷密度越大，该地区(用户)的用电量就越大，变压器的容量也就越大.并且，负荷密度大的用户，通常变压器的负载率都比较高，用户需报装变压器的可能性就越高.

(2)年用电量增长率(X2)

年用电量增长率是指用电用户本年度用电量相对于上一年度用电量的增长率.计算公式如下：

(2)

式中，P1为用电用户上一年度用电量，P2为用电用户本年度用电量.年用电量增长率反映了负荷的增长水平，通常负荷增长越快，变压器的负载率就会越高，用户需报装变压器的可能性就越高.

(3)配变投运时间(X3)

配变投运时间是指用电用户的配电变压器的投运年份到当前年份的时间.通常用电用户的负荷水平都要经历增长到饱和甚至是衰减的过程.不同时间段用电用户的负荷水平不同，对变压器的负载率的影响较大.用电用户的配变投运时间可以大致地反映这个变化的过程.

2基于模糊聚类的实用系数等级划分及选取方法

传统的实用系数选取都采用统一的标准值或依靠工作人员的经验，每一类用电用户只有一个标准值，灵活性和适应性较差.模糊聚类能够根据研究对象本身的属性，将各类用电用户中特征相近的样本划分为一类，从而实现对各类用户的进一步细分，大大改善了选取的灵活性，并提高了实用系数的计算精度.

2.1实用系数等级的模糊聚类分析

模糊聚类分析是一种数据划分或分组处理的重要手段和方法，其主要原理是根据某些特定的标准和规则，衡量各个样本之间的相似性，并将具有相似统计特征的数据划分成一类[17- 18].文中提出的模糊聚类[19- 20]分析方法的具体流程如下.

(1)数据获取及标准化处理

设论域X={x1,x2,…,xn}为被分类的对象，每个对象又包含m个评价指标，构成如下的原始数据矩阵：

其中，xnm表示第n个对象的第m个评价指标的原始数据.

为了使不同量纲的各评价指标之间也能进行比较，必须对原始数据进行标准化处理.通常的做法是对原始数据做适当的变换，将除去量纲影响的数据压缩到区间[0，1]上.文中采用的方法主要是平移-标准差变换以及平移-极差变换[21].

(2)建立模糊相似矩阵

为了构建模糊相似矩阵，需根据步骤(1)中标准化处理后的数据计算其相似系数.相似系数rij的求解主要有欧氏距离法、相似系数法以及海明距离等方法，文中采用欧氏距离法，具体的计算方法为

(3)

式中：参数c要适当选取，确保0≤rij≤1.根据计算结果，可得到模糊相似矩阵R=(rij)m×m.

(3)聚类

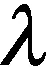
(4)聚类结果分析

根据流程(3)中的动态聚类结果，将各类用户的实用系数划分成不同的等级，具体的步骤如下：

(4)

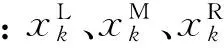
步骤3将步骤2中的k类样本按照实用系数的中心值从大到小排列，形成k个实用系数等级.

2.2实用系数的选取方法

实用系数的选取就是根据待测用电用户的评价指标来确定用电用户所属的实用系数等级，并求得实用系数值.具体的选取方法为：①判断待测用电用户的评价指标X1、X2、X3是否全部落在某个实用系数等级的评价指标范围内，如果是，则判定待测用电用户属于该等级；②如果不能直接判定，则可将待测用电用户的评价指标和2.1节求得的所有等级的实用系数的评价指标中心值构成矩阵，将矩阵标准化处理后，计算待测用电用户各评价指标与各个等级的评价指标中心值的加权距离之和，和越小表示该用户的实用系数与该实用系数等级越接近，距离最小的实用系数等级即为待求用电用户的实用系数等级，进而确定该用户的实用系数值.计算方法为

d=[w1(r1-r01)2+w2(r2-r02)2+…+

wm(rm-r0m)2]1/2

(5)

式中：d为加权距离和；rm为标准化处理后的待测用电用户的评价指标值；r0m为标准化处理后对应的某个等级评价指标中心值；m为评价指标个数；w为各评价指标权重系数；w的确定方法一般有层次分析法、变异系数法和熵权法等[22]，文中采用变异系数法来确定各评价指标的权重[14].

3实用系数指标分析方法及流程设计

文中设计的实用系数指标分析方法主要包括了对现有样本集的实用系数等级划分以及待测用电用户实用系数的确定两个部分.具体的流程为：首先，划分用电用户的类型，确定待测用电用户的类型，构建相应的评价指标，并求得各样本的评价指标值及实用系数值；然后，运用模糊聚类方法对这些样本的实用系数划分等级，获得各等级的评价指标及实用系数的数值的范围，并将它们的平均值设置为中心值；最后，根据待测用电用户的评价指标值与各等级中心值的加权距离和，确定待测用电用户的实用系数等级，并得到相应的实用系数值.

实用系数指标分析流程如图1所示.

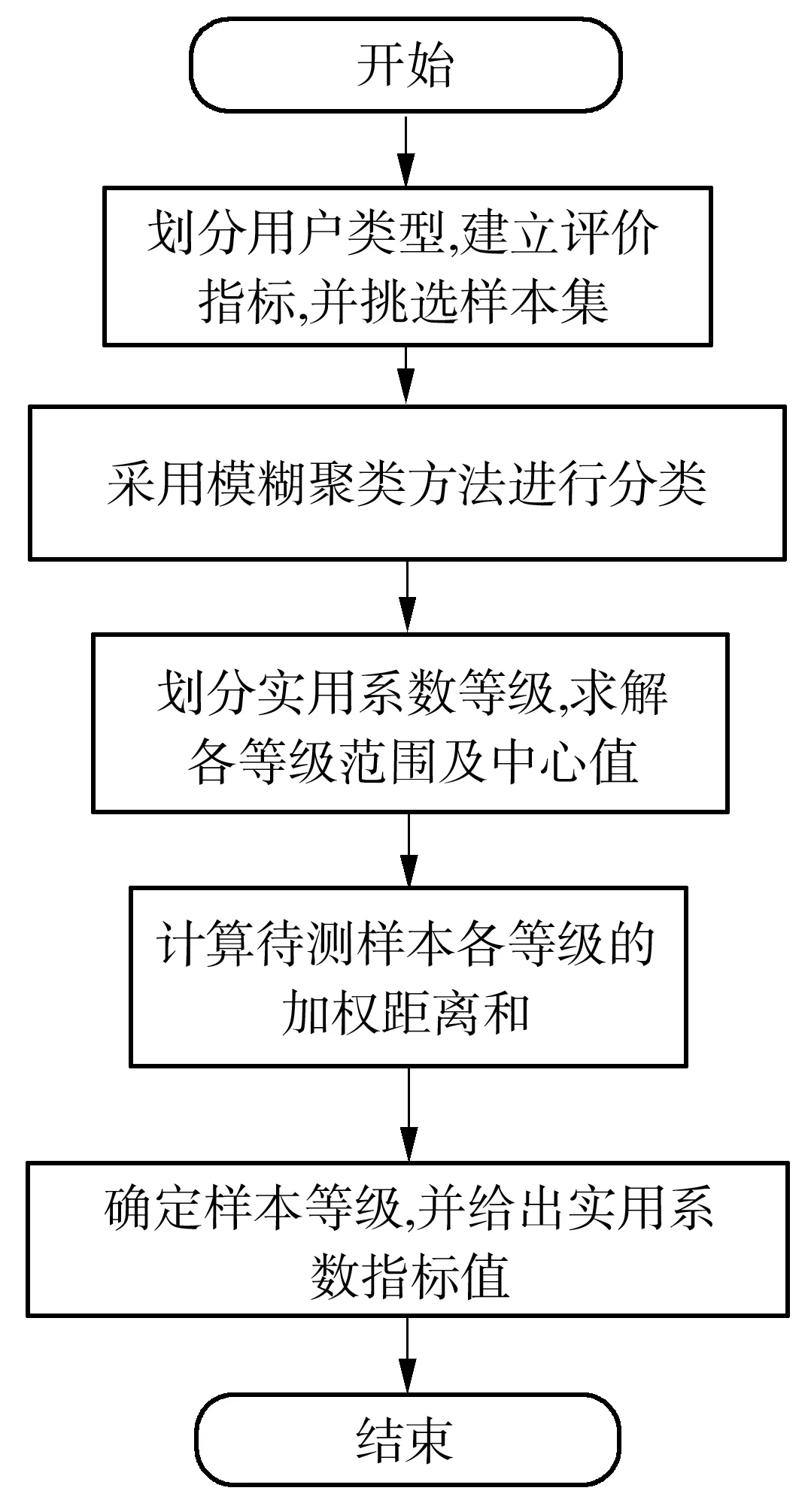
图1　实用系数指标分析流程

4实例分析

由于不同类型用电用户的用电特性不同，业扩报装时的流程也不同，在研究用户的实用系数之前，必须对用电用户进行分类.因此，文中首先将用电用户分为6类：工业用地、住宅用地、办公用地、商业用地、文化娱乐用地、公共设施用地.并以某市住宅用户的实用系数指标分析为例，对文中的实用系数指标分析方法的灵活性和实用性进行验证.

共选取22个住宅样本(其中一个样本代表一个小区)，用电用户的评价指标包括：负荷密度X1、年用电量增长率X2以及配变投运时间X3.根据收集的样本数据可计算得22个样本的实用系数，其中实用系数的计算公式为

(6)

式中，μ为实用系数，N为用户下属配变的台数，Pi为第i台配变的年最大有功负荷，Si为第i台配变的容量.

收集的部分住宅用电用户样本的原始数据如表1所示.

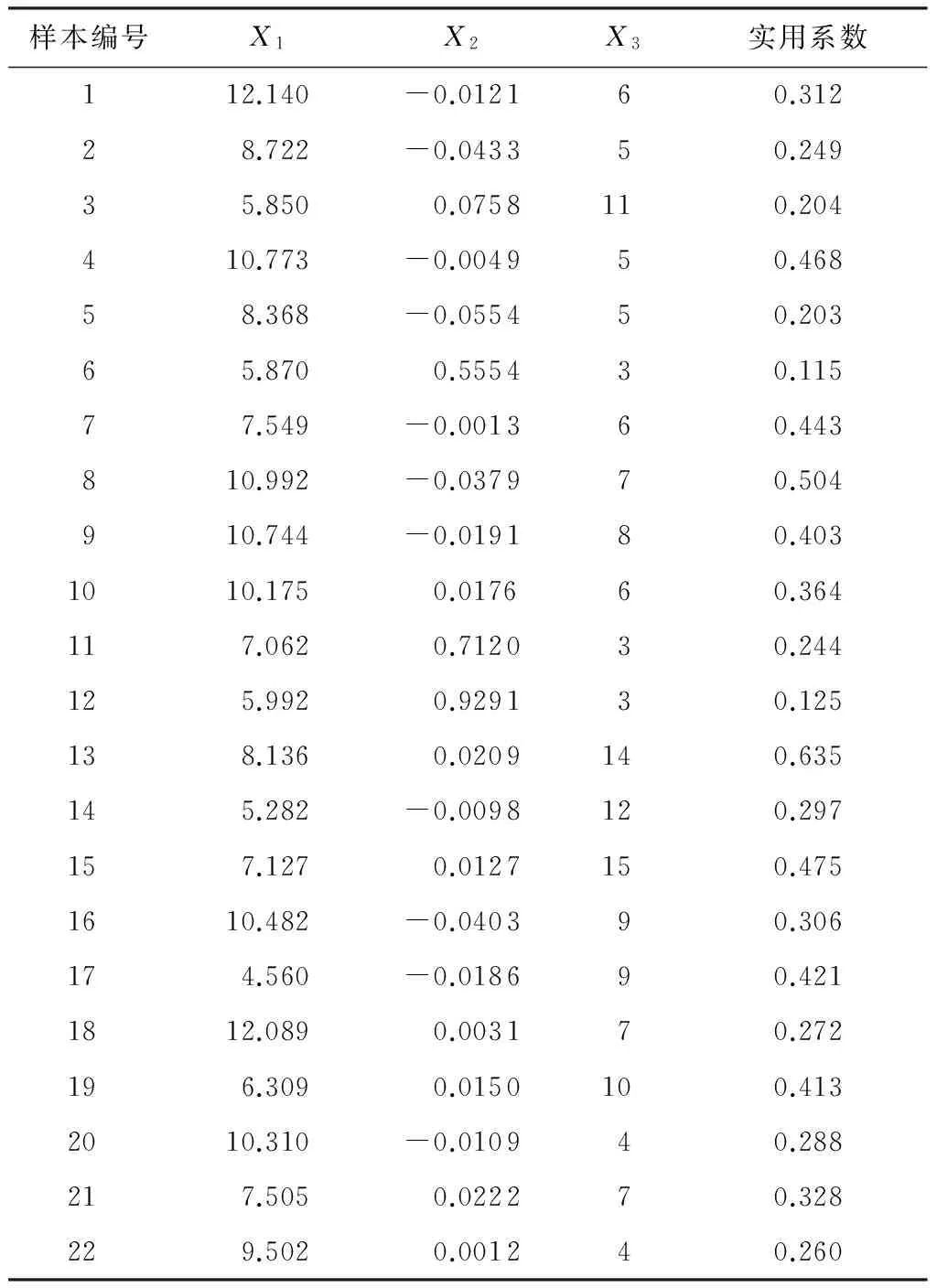
表1　住宅用户样本的原始数据

根据第2.1节的模糊聚类方法的基本流程，可得到动态聚类图，如图2所示.

图2　动态聚类图

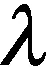
根据分类的结果，可将这4类样本视为4个实用系数等级，并根据式(4)求出各等级的评价指标及实用系数的中心值.按实用系数中心值从大到小排列，计算结果如表2所示.

表2　住宅用户实用系数分类结果

采用差异系数法可求得负荷密度、年用电量增长率以及配变投运时间3个评价指标的权重系数分别为：0.347 1，0.438 9，0.214 0.至此，文中构建了住宅用电用户的4个实用系数等级，并确定了相应的评价指标范围以及各评价指标的权重.

从分类的结果可以看出:第1类用户的负荷密度较高，负荷的增长较慢，配变投运时间较长，表示这类用户的发展时间较长，其负荷已经到达稳定的阶段，实用系数较高；第2类用户的各项评价指标的波动范围都比较大，表示这类负荷的发展具有较大的不确定性，其实用系数的波动范围也相对较大；第3类用户的负荷密度较低，负荷的增长较慢，配变投运时间较长，表示这类用户也处于稳定的阶段，但与第1类相比，其负荷密度和实用系数明显偏低；第4类用户的负荷密度较低，配变投运时间较短，但其年电量的增长非常快，说明这类用户是新用户，其负荷处于快速增长的阶段，其实用系数较小，但增长很快.

在实际的业扩报装工作中，应当重点关注第2类用户中负荷密度高、年用电量增长快、实用系数较高的用户，这些用户的变压器利用率较高，且负荷发展较快，其报装变压器的需求较大.

为了验证实用系数等级划分的正确性，将样本1当作待测用电用户，求解样本1的实用系数.该样本评价指标的模糊集为[12.140，-0.012 1，6]，与表2中所有实用系数等级的评价指标中心值构成的矩阵为

对X矩阵进行标准化处理，可得矩阵：

根据式(5)计算出待测用电用户与各个实用系数等级的评价指标的中心值的加权距离为

d=[0.594 70.194 60.616 80.848 4].

可以看出，待测用电用户与等级2的距离最小.因此，认为该用户属于等级2，该等级实用系数的范围为0.203～0.504，中心值为0.338，而该样本实际的实用系数为0.312，与该等级的中心值相当贴近.从而证明了文中提出的方法的正确性.

5结论

(1)首次设计了基于模糊聚类的实用系数指标分析方法.该方法能根据样本的评价指标客观地进行分类，克服了传统方法依靠工作人员经验和主观判断、无法系统化处理大规模数据的缺陷，能够真实客观地反应该地区用电用户的实用系数的实际水平.

(2)所设计的模糊聚类方法能够进一步细化各类用电用户的实用系数等级.该方法既给出了实用系数的范围，同时给出了具体的实用系数估算值.在确定不同的实用系数等级后，能够根据待测用户的评价指标，简单快速地算出待测用户的实用系数等级及实用系数值.解决了目前各类用电用户仅有一个实用系数标准值、划分不够细致的问题，大大改善了实用系数选取时的灵活性，提高了计算精度.

(3)首次引入配变投运时间作为评价指标来表示负荷发展特性.在对用电用户进行模糊聚类时，除了考虑用户的负荷密度、年用电量增长率等因素以外，还引入配变投运时间评价指标来描述负荷的发展特性，充分考虑负荷的发展对实用系数的影响，使得聚类的结果更加准确.

(4)设计了良好的评价指标体系，综合考虑了容量、面积和时间等因素.在实际应用中，用电用户实用系数的评价指标可能会因社会经济、用户类别等条件的不同而有所区别，不同地区所能获取的数据也各有不同，因此，必须根据本地区的实际情况选取适当的评价指标.

(5)设计的算法主要针对业扩报装的用户.当用户还没入住时，确定其所需配变容量属于负荷预测的范畴，不在文中研究的范围内.

综上所述，文中所提出的基于模糊聚类的实用系数指标分析方法操作简单，计算结果精确可靠，根据聚类结果对各类型用户的实用系数划分等级，可使结果更符合实际应用要求，具有较高的推广价值.实例分析表明，该方法具有有效性和适用性，能够科学地指导业扩报装工作，提高设备的利用率.

参考文献：

[1]张金娥.影响电力业扩报装速度的因素及解决方法 [J].电力需求侧管理,2011,13(5):63- 65.

ZHANG Jin-e.Factors affecting the speed of power business expending and its solutions [J].Power Demand Side Management,2011,13(5):63- 65.

[2]余向前,王林信,张维静,等.基于生长曲线的行业业扩用电趋势研究 [J].电力需求侧管理,2014(2):21- 25.

YU Xiang-qian,WANG Lin-xin,ZHANG Wei-jing,et al.Research of business expanding electric consumption trend based on growth curves [J].Power Demand Side Management,2014(2):21- 25.

[3]齐志刚,金波,邱朝明.基于GIS的业扩报装优化与决策系统设计 [J].中国电力,2011,44(1):90- 94.

QI Zhi-gang,JIN Bo,QIU Chao-ming.GIS based optimal design of electric expansion,installation and decision-making system [J].Electric Power,2011,44(1):90- 94.

[4]HUMAYUN M,SOUSA B J O,SAFDARIAN A,et al.Optimal capacity management of substation transformers over long-run [J].IEEE Trans on Power Systems,2016,31(1):632- 641.

[5]GILVANEJAD M,GHADIRI H,SHARIATI M R.et al.Analyzing the effect of transformer utilization factor in distribution networks as an investment management index by using displan software [C]∥Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution(CIRED 2013).Stockholm:[s.n.],2013:1- 4.

[6]冯浩,曹云轩,彭子耀,等.基于动态负荷的变压器容量阶梯型配置方案 [J].电测与仪表,2014,51(13):112- 117.

FEND Hao,CAO Yun-xuan,PEND Zi-yao,et al.Transformer capacity ladder-type configuration plan based on dynamic load [J].Electrical Measurement and Instrumentation,2014,51(13):112- 117.

[7]肖白,周潮,穆钢.空间电力负荷预测方法综述与展望 [J].中国电机工程学报,2013,33(25):78- 92.

XIAO Bai,ZHOU Chao,MU Gang.Review and prospect of the spatial load forecasting methods [J].Proceedings of the CSEE,2013,33(25):78- 92.

[8]周湶,孙威,张昀,等.基于改进型ANFIS的负荷密度指标求取新方法 [J].电力系统保护与控制,2011,39(1):29- 34,39.

ZHOU Quan,SUN Wei,ZHANG Yun,et al.A new method to obtain load density based on improved ANFIS [J].Power System Protection and Control,2011,39(1):29- 34,39.

[9]韩俊,谈健,黄河,等.基于改进K-means聚类算法的供电块划分方法 [J].电力自动化设备,2015,35(6):123- 129.

HAN Jun,TAN Jian,HUANG He.Power-supplying block partition based on improvedK-means clustering algorithm [J].Electric Power Automation Equipment,2015,35(6):123- 129.

[10]GAO Yan,YANG Ren-gang,LI Wei.A spatial load density forecasting method based on cloud theory and fuzzy analytic hierarchy process [C]∥Proceedings of Electricity Distribution(CICED),2012 China International Conference on IEEE.Shang hai:[s.n.],2012:1- 4.

[11]WASILEWSKI Jacek.Spatial electric load forecasting using fuzzy cellular automata technique [C]∥Proceedings of Universities’ Power Engineering Conference(UPEC).Soest:[s.n.],2011:1- 6.

[12]CARRENO E M,PADILHA-Feltrin A.Evolutionary heuristic to determine future land use [C]∥Proceedings of Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century.Pittsburgh:Curran Associates,Inc,2009:1- 6.

[13]周湶,孙威,任海军,等.基于最小二乘支持向量机和负荷密度指标法配电网空间负荷预测 [J].电网技术,2011,35(1):66- 71.

ZHOU Quan,SUN Wei,REN Hai-jun,et al.Spatial load forecasting of distribution network based on least squares support vector machine and load density index system [J].Power System Technology,2011,35(1):66- 71.

[14]吴冰,张筱慧.模糊数与多指标灰靶决策理论相结合的小区负荷预测方法 [J].电力系统保护与控制,2011,39(11):124- 128.

WU Bing,ZHANG Xiao-hui.Application of fuzzy number and multi-attribute weighted grey target theory in small area load forecasting [J].Power System Protection and Control,2011,39(11):124- 128．

[15]肖白,聂鹏,穆钢,等.基于多级聚类分析和支持向量机的空间负荷预测方法 [J].电力系统自动化,2015,39(12):56- 61.

XIAO Bai,NIE Peng,MU Gang,et al.A spatial load forecasting method based on multilevel clustering analysis and support vector machine [J].Automation of Electric Power Systems,2015,39(12):56- 61.

[16]肖白,杨修宇,穆钢,等.基于元胞历史负荷数据的负荷密度指标法 [J].电网技术,2014,38(4):1014- 1019.

XIAO Bai,YANG Xiu-yu,MU Gang,et al.A load density index method based on historical data of cell load [J].Power System Technology,2014,38(4):1014- 1019.

[17]曲福恒,崔广才.模糊聚类算法及应用 [M].北京:国防工业出版社,2011:46- 60.

[18]李怀俊,谢小鹏,黄恒.基于主元熵的发动机能量数据聚类与故障识别 [J].华南理工大学学报(自然科学版),2013,41(11):137- 142.

LI Huai-jun,XIE Xiao-peng,HUANG Heng.Energy data clustering and fault recognition of engine based on principal component entropy [J].Journal of South China University of Technology(Natural Science Edition),2013,41(11):137- 142.

[19]TAN Pang-ning,STEINBACH Michael,KUMAR Vipin.Introduction to data mining [M].范明,范宏建,译.北京：人民邮电出版社,2014:30- 31.

[20]范金城,梅长林.数据分析 [M].2版.北京:科学出版社,2010.

[21]杨德平,刘喜华,孙海涛,等.经济预测方法及Matlab 实现 [M].北京：机械工业出版社,2012.

[22]王化中,强凤娇,陈晓暾.模糊综合评价中权重与评价原则的重新确定 [J].统计与决策,2015,31(8):24- 27.WANG Hua-zhong,QIANG Feng-jiao,CHEN Xiao-tun.The redefinition of weight and evaluating principle on fuzzy comprehensive evaluation [J].Statistics and Decision,2015,31(8):24- 27.

Analysis Method of Practical Coefficient Based on Fuzzy Clustering

OUYANGSenWUYu-shengFengTian-rui

(School of Electric Power∥Key Laboratory of Clean Energy Technology of Guangdong Province, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:Practical coefficient is usually applied to the selection of distribution transformer capacity for the business expending. As the existing practical coefficient selection methods with low flexibility are greatly affected by dataand do not take into consideration the load development feature, a method to analyze the practical coefficient based on fuzzy clustering is proposed. In this method, first, power usersare divided into such three types as business, house and industry, and the corresponding evaluation indexes, namely the load density, the annual growth rate of electri-city consumption and the commission time of distribution transformer, are used to describe the power consumption level and its variation as well as the load development feature of power users. Then,a classification method of practical coefficient levels is designed based on the fuzzy clustering, which uses the three above-mentioned evaluation indexes to perform a fuzzy clustering for the coefficient level classification and determines the evaluation index and practical coefficient’s central value of each classification. Finally, the level and value of the practical coefficient of a new power user are obtained according to the sum of the weighted distance between the index value and the central value of each classification. In addition, the effectiveness and practicability of the proposed method are verified through a case study.

Key words:practical coefficient; fuzzy clustering; central value; business expending

收稿日期:2015- 06- 01

*基金项目:国家自然科学基金重点资助项目(51377060)；国家自然科学基金青年基金资助项目(61104181)

Foundation items: Supported by the Key Program of National Natural Science Foundation of China(51377060) and the National Natural Science Foundation for Young Scholars of China(61104181)

作者简介:欧阳森(1974-)，男，博士，副研究员，主要从事电能质量、节能技术与智能电器等的研究.E-mail:ouyangs@scut.edu.cn

文章编号:1000- 565X(2016)04- 0040- 07

中图分类号：TM 711

doi：10.3969/j.issn.1000-565X.2016.04.007