有关弹簧的串并联问题及解答方法

罗泽怀

摘要：本文通过对胡克定律的拓展，即对有关弹簧的串并联问题做了简单的剖析，从而使同学们看了后有一个更深刻的认识和理解。

关键词：弹簧；串联；并联

中图分类号：G632 文献标识码：B 文章编号：1002-7661（2016）13-175-01

现在我们刚好学到胡克定律，设计到弹簧问题，但针对弹簧的串并联及其解答方法来说，同学们还不怎么理解，对他们而言既是重点，也是难点。就此问题说说我对它的一些理解：

一、弹簧的“串联”

1、首先什么是弹簧的串联呢？（如图二所示）两弹簧相串构成新弹簧的劲度系数为K=K1K2/K1+K2，我们把弹簧相串使用叫弹簧“串联”。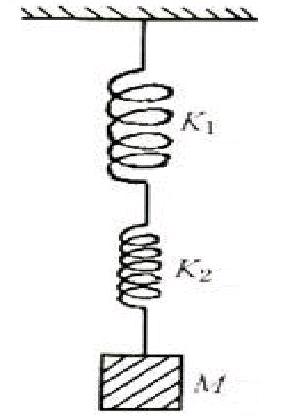

2、解题思路：即两个弹簧串联时，每个弹簧受力都是F，因此有

F=k1x1F=k2x2F=Kx∵x=x1+x2

∴F/k=F/k1+F/k2

即1/k=1/K1+1/k2，或K=k1k/（k1+k2）

（图二）

n个弹簧串联，根据所受弹力相等

x1=F/k1，x2=F/k2，……，xn=F/kn

∵x=x1+x2+……+xn

∴F/K=F/k1+F/k2+……+F/kn

即1/K=1/k1+1/k2+……+1/kn（恰好是电阻并联的情况）

3、应用：例1已知弹簧A的劲度系数为k1=100N/cm，弹簧B的劲度系数为k2=200N/cm，如果把两弹簧相串使用，在弹簧末端挂一个重为G=30N的物体，求弹簧相串后的等效劲度系数k。

解析如图二所示，两弹簧相串使用，当挂上重物，弹簧A、B所受的拉力均为G。设弹簧A的伸长量为，弹簧B的伸长量，则有

（1） G=K1X1X1=G/K1=30N/100N/cm=0.3cm

（2） G=K2X2X2=G/K2=30N/200N/cm=0.15cm

由上面两式得相串弹簧的伸长量为X=X1+X2=0。3+0。15=0。45 习题：一根轻质弹簧下面挂一重物，弹簧伸长了X1，若将该弹簧剪去，在剩下的部分下端仍然挂原重物，弹簧伸长了X2，则X2∶X1为：

A、3∶4 B、4∶3 C、4∶1 D、1∶4

解析设轻质弹簧原长为L0，则该弹簧等效于4个原长为L0的轻质弹簧的“串联”，设原轻质弹簧的劲度系数为K，则由前面的推导知，小弹簧的劲度系数K/4。所以，在弹簧剪断前后挂同一重物，应有，把代入上式得答案为C。

易混淆题：已知物块A、B的质量均为m，两轻质弹簧劲度系数分别为K1和K2，已知两弹簧原长之L1和L2为，不计两物体的厚度，求两弹簧的总长度为_____。

错解两弹簧是“串联”，由推导知，弹簧串后的劲度系数为，设两弹簧压缩量为，由胡克定律得，把代入得，所以两弹簧的长度为。

错解剖析解答错误的原因是不经分析就把该题中两弹簧看成“串联”。

正确解答由题意知，上面轻质弹簧上的受力为mg，下面弹簧的受力为2mg，设上面弹簧压缩量为，下面弹簧的压缩量为，由胡克定律易得mg=K1X1X1=mg/K12mg=K2X2X2=2mg/K2因此知题中弹簧的长度为X=L1+L2-（X1+X2）=L1+L2-（mg/K1+2mg/K2）

二、弹簧“并联”

1什么叫弹簧的并联？如图三所示两弹簧相并构成新弹簧的劲度系数为K=K1+K2。我们把弹簧相并使用叫做弹簧“并联”。

2解题思路：两个弹簧并联时，各受力为F/2，两弹簧的形变两相同，因此有F/2=k1x1F/2=k2x2

F=Kx∵F=F/2+F/2

∴kx=k1x1+k2x2∴K=k1+k2

n个弹簧并联，各弹簧伸长量相等

k1x+k2x+k3x+……+knx=F=Kx （k1+k2+k3+……+kn）x=Kx

即K=k1+k2+k3+……+kn（恰好是电阻串联的情况）

3、应用：例2已知弹簧A的劲度系数为K1=250N/cm，弹簧B的劲度系数为K2=150N/cm，如果把两弹簧相并后，在弹簧的末端挂一重物G=50N，求弹簧相并后的等效劲度系数K。

解析：如图三所示，两弹簧相并使用，当挂上重物后，两弹簧A、B伸长量相同，设两弹簧的伸长量均为X，由平衡条件得，即，K=K1+K2=250N/cm+150N/cm=400N/cm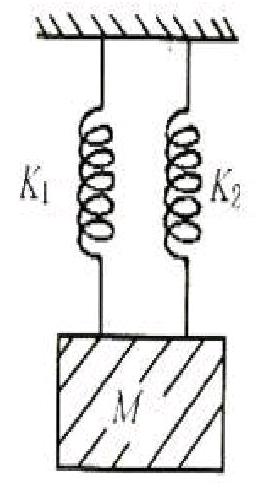

习题：如例三图所示，a、b两根轻质弹簧，它们的劲度系数分别为k1=120N/cmk2=150N/cm，在下端挂一重物G，物体受到的重力为10N，平衡时物体下降了______cm。

解析由上面的推导知，a、b并联后弹簧的劲度系数为k=k1+k2=270N/cm，由胡克定律可知G=KXX=G/K=10/270N/cm=1/27cm。

易混淆题：两根原长相同的轻质弹簧A、B竖直悬挂，其下端用一根跨过动滑轮的细绳连在一起，不计绳与滑轮的质量，两弹簧原来均无形变，求在动滑轮下挂一质量为的m砝码后，动滑轮下降了多大？已知弹簧劲度系数分别为k1，k2，弹簧始终保持弹性形变。

错解剖析解答错误的原因是把A、B两弹簧看成“并联”，其实不然，该题中的弹簧与“并联”的区别在于，弹簧“并联”时，弹簧末端挂一重物，两弹簧的伸长量相同。该题中的两弹簧通过绳绕过滑轮相连，两弹簧上的拉力大小相等，均为，两弹簧伸长量并不相等。

正确解答：设弹簧A的伸长量为，弹簧B的伸长量为，则由平衡条件可求得。

【总结】弹簧串联时各弹簧受力相等，关联时各弹簧伸长量相等，再由胡克定律推导出等效劲度系数K，各弹簧串并联的劲度系数K情况恰好与电阻的串并联情况相反。

因此弹簧的串并联问题，只要同学们理解了上述两种情况后，我们在解决这类型的题时，基本上的问题都能解决了。