基于滑模变结构方法的APF电流控制策略

2016-07-02黄晶晶孙元岗同向前西安理工大学自动化与信息工程学院陕西西安710048

电气传动 2016年5期

黄晶晶，孙元岗，同向前（西安理工大学自动化与信息工程学院，陕西西安710048）

基于滑模变结构方法的APF电流控制策略

黄晶晶，孙元岗，同向前
（西安理工大学自动化与信息工程学院，陕西西安710048）

摘要：采用比例积分（PI）调节器的滞环空间矢量PWM（HSVPWM）控制系统难以确保有源电力滤波器（APF）遭受未知扰动或者运行状态发生变化时系统的控制性能。针对该问题，提出一种基于滑模变结构方法的滞环空间矢量控制，以有效提高APF系统的暂态控制性能。电压外环采用滑模变结构控制，以克服传统PI调节器抗扰动能力差等问题。在电流内环，当系统电流偏差被控制在一定范围内时，开关状态的选择以降低系统的开关损耗为目标；当系统电流偏差较大时，开关状态的选择以提高暂态响应速度为目标。与采用传统PI控制器的HSVPWM控制策略进行仿真对比，结果表明所提控制策略的暂态响应时间减少了25%以上；并利用实验结果进一步验证了所提策略的可行性。

关键词：有源电力滤波器（APF）；电流控制；滞环空间矢量；滑模变结构；比例积分（PI）

近年来，随着电力电子装置在电力系统中的大量使用，不断向电网注入无功和谐波成分，致使电网电压出现三相不平衡、闪变及谐波等问题，影响着电网的利用效率和电能质量，甚至还会威胁电网安全。有源电力滤波器（APF）作为一种有效的谐波抑制和无功补偿设备，逐渐成为工程领域争相研究的热门课题［1-2］。

在多数应用场合，并联型APF采用电压型功率变换器。通常APF需要实现2个控制目标：一是将直流侧电压控制在给定的目标值，以抵御电网电压和负载波动的影响，保持系统稳定性；二是控制变换器实现电流的跟踪控制，使系统获得高功率因数和较高质量的电流波形［3-4］。

为了实现上述控制目标，绝大多数的APF控制系统都采用双闭环控制结构。外环控制器负责稳定直流侧电压，通常采用比例积分（PI）调节器，传统PI调节器的P，I参数依赖于被控对象，所以当系统运行环境改变时，传统PI调节器将难以保证系统的动态特性，甚至会引发系统振荡，严重影响APF装置的正常运行［5-7］。

内环控制器常采用电流控制，APF常用的电流控制方法包括滞环控制和空间矢量控制。在三相静止坐标系下的电流滞环控制设计原理简单，易于实现，不受系统参数影响，能够获得快速的动态响应和较高的电流控制精度。但这种控制策略会使得功率开关管的工作频率不固定，不利于网侧滤波器设计，还会带来较高的开关应力［8-9］。在两相同步旋转坐标系下，电流内环的各交流分量均被转换为直流分量，可以很方便地采用空间矢量PWM（SVPWM）控制。这种控制能得到固定的开关频率，便于系统参数设计，是目前应用比较广泛的控制策略，但其在控制精度及动态响应方面要稍逊于滞环控制［10］。结合上述两种控制策略的优缺点，近年来有学者提出了一种滞环空间矢量（HSVPWM）控制，利用电流偏差矢量的空间位置和不同开关状态对电流偏差变化率的影响，选择最佳的开关状态。这种控制方法已经在有源电力滤波器、并网逆变器等电力电子相关领域得到了广泛应用［11-12］。

综上所述，本文提出一种基于滑模变结构方法的HSVPWM控制策略，电压外环采用滑模变结构控制，以克服传统PI调节器抗扰动能力差等问题。在电流内环，当系统电流偏差被控制在一定范围内时，开关状态的选择以提高系统的控制精度为目标；当系统电流偏差较大时，开关状态的选择以提高暂态响应速度为目标。与采用PI控制器的HSVPWM控制策略的仿真对比，进一步验证了所提控制策略的优越性；最后开展所提HSVPWM在实验系统中的可行性分析。

1　APF数学模型

图1为APF主电路结构图，主要包括3个部分：供电系统、由三相不控桥整流电路构成的非线性负载和由VSC构成的APF主电路。其中，ea，eb，ec分别为供电系统电压，ia，ib，ic分别为系统侧电流，iLa，iLb，iLc分别为负载侧电流，iCa，iCb，iCc分别为APF交流侧电流，ua,ub,uc为APF中VSC变换器交流侧输入电压；udc为APF直流侧电压。APF装置并联在交流系统中，主要用于补偿系统中的谐波和无功成分。三相桥式不控整流装置作为谐波源，主要负责产生谐波。L0为非线性负载侧的滤波电感；L1为APF的滤波电感；Sk，-Sk(k=a,b,c)代表APF 6只IGBT开关管的工作状态，Sk=1 (k=a,b,c)表示开关管导通；Sk=0 (k=a,b,c)表示开关管关断。其中-Sk=1-Sk。

图1　APF系统Fig.1 APF system

根据图1，可以得到以下数学模型：

将式（2）代入式（1），可以得到：

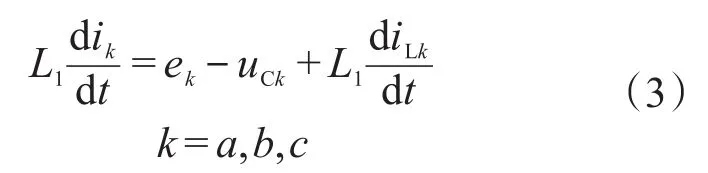
将式（3）用矢量形式表达如下：

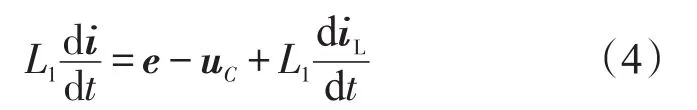
令Δi=i*-i，代入式（4）：

对于APF三相电压型变换器而言，uC包含8个电压矢量uCm（m =0～7），由不同的开关状态决定，也称之为开关矢量。因此，可以得到：

由上述推导可知，系统侧电流误差矢量的变化率受uCm，e指令电流i*变化率以及负载电流iL变化率影响，假设变换器侧三相输入电压合成矢量u*满足：

将式（6）代入式（5）后得到：

由式（6）可以看出，电压矢量u*是不可控制的，但式（7）中的电压矢量uCm是可以选择的。因此，通过选择合适的uCm可以控制Δi的变换率，进而达到控制交流侧电流的目的，这是HSVPWM的基本控制思想。

2　滑模变结构控制器设计

结合上述控制思想，图2给出了本文所采用的HSVPWM控制框图。直流侧电压给定值和实际值Udc作比较后送入电压控制器；电压控制器的输出为电流指令值，对应于系统交流侧电流的幅值。因此，乘以与电源电压同相位的余弦信号cos(ωt+2mπ/3)（m=0,1,2）就可以得到系统侧电流给定信号。与实际采集到的系统侧电流信号作比较后送入滞环比较器，根据滞环比较器输出的状态值确定系统电流偏差矢量Δi的扇区。与此同时，利用采集到的电源电压eabc和电流给定信号可以得到电压空间矢量u*所在的扇区。一旦确定了u*和Δi的空间位置，选择恰当的开关矢量uCm使电流偏差矢量的变化率L1dΔi/dt与Δi方向相反，就能够将Δi限制在合理的范围内。

传统HSVPWM控制中的电压外环多采用PI控制器，难以应对外部扰动等干扰问题，针对该问题，图2中电压外环控制器采用滑模变结构控制器来完成，具体设计过程如下。

图2　HSVPWM控制图Fig.2 Control principle of HSVPWM

式（1）～式（3）为APF在三相abc坐标系下的方程，对其进行坐标变换，将其从三相静止坐标系下变换到两相同步旋转坐标系下，变换后可以得到APF与系统侧交换的瞬时功率为

通过坐标变换，可以将静止坐标系下变化的参数ia，ib和ic变换成同步旋转坐标系下面的直流量id，iq，将ea，eb和ec变换为ed，eq。通过控制id，iq，就可以控制有功功率P和无功功率Q。

假设APF维持直流侧电容电压稳定性的有功功率为PC，负载正常运行消耗的有功功率为PL，利用式（8）中系统侧送出的有功功率P，可以得到：

P=PL+PC（9）

其中PC=αP0＜α＜1

结合式（8）所示瞬时功率表达式，可以得出：

定义直流侧电压偏差：e=Udc*-Udc，为了提高系统鲁棒性，消除稳态误差，在电压环滑模面引入积分项：

其中β1＞0 β2＞0 β3＞0

因此，可以获得：

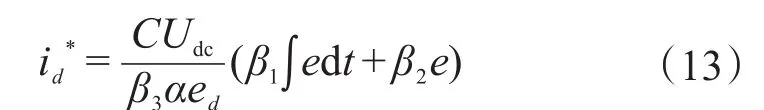
设电压外环的李雅普诺夫函数为

对式（14）求导后可以得到：

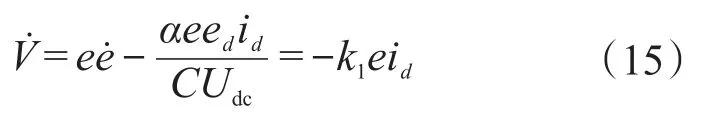
将式（13）代入式（15）后，可以推导出：

因此，利用式（13）所设计的电压控制器，能够有效保证电压外环的稳定性，实现直流侧电压的实时跟踪控制。

综上所述，此处利用式（13）完成电压外环中滑模变结构控制器的设计，其中β1＞0, β2＞0,β3＞0,0＜α＜1。可在仿真软件中完成式（13）中参数的选择，并将其作为实际APF装置中控制器设计过程的参考值。

3　仿真和实验研究

3.1仿真验证

为了验证所提出滑模变结构控制器的可行性和优越性，按照图1和图2所示的APF主电路和控制框图在Simulink下构建系统仿真模型。仿真模型参数分别为：系统侧相电压峰值200 V，APF与负载侧均采用1 mH滤波电感，APF与负载侧均采用2 400 μF直流电容。开关频率由所采用的定时器决定，设置为10 kHz。图3为采用传统PI控制和所提滑模变结构控制器的对比结果。

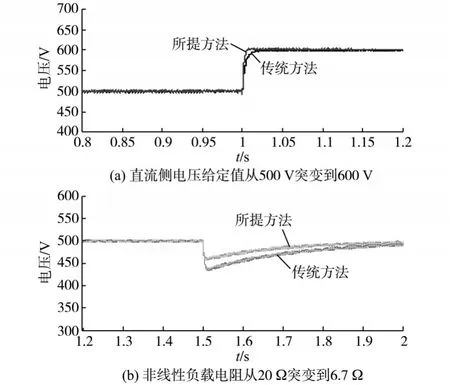
图3　仿真结果Fig.3 Simulation results

图3a中：在t =1 s时，令直流侧电压给定值从500 V突变到600 V。传统PI控制器下，APF直流侧电压需要16 ms的时间才能达到稳态；对于所提滑模变结构控制器而言，APF直流电压仅需要7 ms即可被调整到稳态，直流侧电压的暂态响应时间减少了56.25%。

为了验证所提方法的扰动抑制能力，图3b中：在t =1.5 s时，令非线性负载侧的负载电阻从20 Ω突变到6.7 Ω。传统PI控制器下，APF直流侧电压需要0.4 s的时间来到达新稳态；所提方法需要0.3 s即可进入新稳态，暂态时间减少了25%。

根据以上仿真结果可以得出结论：与传统PI控制方法相比，所提出的滑模变结构控制方法，能够有效提高APF系统的暂态响应速度及抗扰动能力。

3.2实验验证

为了进一步验证所提控制策略在实际系统中的可行性，根据仿真模型搭建50 kW的APF实验模型，系统侧电压峰值由隔离变压器获得，选择150 V接口，由于隔离变压器设计上的偏差，实际获得的系统侧相电压有效值仅为96 V。其他电路参数与仿真参数保持一致。具体实验电路如图4所示。

图4　实验电路Fig.4 Experiment circuit

图5a为未加入APF时，a相系统侧电压电流波形，此时系统侧电流畸变严重，由电能质量分析仪可以获得此时电流的谐波总畸变率（THD）为22%。

图5b为加入APF后，a相系统侧电压电流波形，此时系统侧电流质量得到了有效提高，为平滑的正弦波，电流的THD值降低到了4%；与未加入APF相比，电流THD值降低了81.8%，电流质量得到了明显的改善，而且电压电流相位基本一致，确保了系统侧的功率因数。

为了更形象地对比APF加入后系统的控制效果，图5c给出了a相系统侧电压电流、APF侧电流及负载侧电流波形，系统侧电流经APF的谐波补偿后克服了电流的畸变问题，得到了高质量的正弦波，该实验结果进一步验证了所提控制策略的有效性。

图5　实验结果Fig.5 Experiment results

4　结论

电力电子装置的大量投入使用加重了电力系统的谐波污染问题，通过建立APF的数学模型，分析了滞环空间矢量的基本工作原理，提出在电压外环采用滑模变结构控制器来提高APF直流测电压的暂态响应速度和扰动抑制能力。仿真和实验结果验证了所设计控制器的优越性及其在实际系统中的可行性，有效克服了传统PI控制器依赖于系统参数，抗扰动能力差等问题，为滑模变结构控制器在APF中的推广应用提供了依据。

参考文献

［1］Acuna P，Morán L，Rivera M，et al. Improved Active Power Filter Performance for Renewable Power Generation Systems ［J］. IEEE Transactions on Power Electronics，2014，29（2）：687-694.

［2］杨龙月，刘建华，王崇林.有源电力滤波器精确反馈线性化准滑模变结构控制［J］.中国电机工程学报，2014，34 （33）：5868-5875.

［3］黄晶晶，张杭，张爱民，等.一种新型并网逆变器电流控制策略的研究［J］.电力系统保护与控制，2011，39（20）：137-140.

［4］Tang Y，Loh P C，Wang P，et al. Generalized Design of High Performance Shunt Active Power Filter with Output LCL Filter ［J］. IEEE Transactions on Industrial Electronics，2012，59 （3）：1443-1452.

［5］Karuppanan P，Mahapatra K K. PI and Fuzzy Logic Controllers for Shunt Active Power Filter—A Report［J］. ISA Transactions，2012，51（1）：163-169.

［6］Narayana G S，Kumar C N，Rambabu C. A Comparative Analysis of PI Controller and Fuzzy Logic Controller for Hybrid Active Power Filter Using Dual Instantaneous Power Theory［J］. International Journal of Engineering Research & Development，2012，4（6）：29-39.

［7］Luo A，Xu X，Fang L，et al. Feedback-feedforward PI-type Iterative Learning Control Strategy for Hybrid Active Power Filter with Injection Circuit［J］. IEEE Transactions on Industrial Electronics，2010，57（11）：3767-3779.

［8］黄晶晶，张爱民，王在福，等.基于模糊滞环的三相电压型整流器直接功率控制［C］//第32届中国控制会议，西安，2013：7590-7594.

［9］肖丽平，童朝南，高润泉.改进的有源电力滤波器滞环电流控制策略［J］.电力系统自动化，2014，38（12）：119-124.

［10］王文，罗安，黎燕，等.一种新型有源电力滤波器的SVPWM算法［J］.中国电机工程学报，2012，32（18）：52-58.

［11］李国华，汪玉凤，高小朋，等.基于滞环SVPWM的有源电力滤波器故障容错方法［J］.电网技术，2014，38（5）：1317-1321.

［12］孙元岗，李宏，石文龙.基于模糊滞环空间矢量的变换器控制策略［J］.电力系统保护与控制，2015，43（8）：69-73.

修改稿日期：2016-04-26

Current Control of APF Based on Sliding Mode Variable Structure Method

HUANG Jingjing，SUN Yuangang，TONG Xiangqian
（School of Automation and Information Engineering，Xi’an University of Technology，Xi’an 710048，Shaanxi，China）

Abstract：It is difficult for the hysteresis space vector PWM（HSVPWM）control to ensure that transient performance using proportional integral（PI）regulator when the active power filter（APF）is suffered from the unknown disturbance or the changing operation state. Therefore，an improved HSVPWM was put forward for the APF based on the sliding mode variable structure. The sliding mode controller（SMC）was adopted to enhance the disturbance rejection ability of the outer DC voltage loop. In the inner current loop of the APF system，if the system current deviation was controlled within a certain range，the selection principle of the proper switching states was to reduce the switching loss. The selection principle of the proper switching states was to enhance the transient performance if the system current deviation was controlled over a certain range. The superiority of the proposed HSVPWM method was verified by the simulation. Compared with the classical PI method，the transient setting time is shortened by at least 25%. Moreover，theeffectivenessoftheproposed method isfurtherdemonstrated viatheexperiment.

Key words：active power filter（APF）；current control；hysteresis space vector；sliding mode variable structure；proportional integral（PI）

中图分类号：TM461

文献标识码：A

基金项目：国家自然科学基金资助项目（51507138）；陕西省教育厅科研计划项目资助（15JK1502）；陕西省重点学科建设专项基金（5X1301）；高等学校博士学科点专项科研基金（20126118110009）；西安理工大学教师科研启动经费项目（103-400211420）

作者简介：黄晶晶（1986-），女，博士，讲师，Email：hjj7759@163.com

收稿日期：2015-09-30

电气传动

2016年5期