基于Contourlet变换的图像自适应阈值去噪方法
2016-07-02李辉姜超
李 辉 姜 超
(中国电子科技集团第二十八研究所 南京 210007)
基于Contourlet变换的图像自适应阈值去噪方法
李辉姜超
(中国电子科技集团第二十八研究所南京210007)
摘要论文研究了一种基于Contourlet变换的图像去噪方法。Contourlet变换是一种有效的图像表示方式,可以更好地表示图像中的边缘信息。根据Contourlet系数的不同特性,论文使用基于系数局部方差的自适应阈值改进了原有阈值,并结合循环平移Contourlet变换改进了阈值去噪算法。实验结果表明,与Contourlet软阈值、Contourlet硬阈值去噪相比,论文算法更好地保留了图像的轮廓细节,提高了图像的PSNR。
关键词Contourlet变换; 去噪; 贝叶斯阈值
Class NumberTP391
1引言
数字图像在采集,传输和存储的过程中,经常由于外部环境和设备的影响不可避免的引入噪声,经过噪声污染的图像显示质量下降,影响视觉效果。图像去噪就是通过相应的算法在尽量保留图像细节的前提下,去除图像中的噪声,从而提高图像质量。
目前常用的图像去噪算法分为空间域方法和频率域法。空间域方法主要是在空间域中对像素灰度值直接进行运算处理,常用方法有均值滤波,中值滤波以及自适应的相关滤波方法等。频率域法是在图像的某个变换域中对图像的变换值进行某种运算处理,较常用的变换有DCT,傅里叶变换,小波变换等。小波变换凭借其良好的时频特性和多尺度特性被广泛地应用在图像去噪领域。但小波变换只有水平,垂直,对角线三个方向,方向与实际图像边缘的多样性不符合,这就需要一种新的图像分析工具。
研究者在小波变换的基础上提出了统称为图像多尺度几何分析工具的一系列图像表示方式,例如Ridgelet(脊波)变换[1],Curvelet(曲线波)变换[2]等。但由于脊波变换和曲线波变换的计算复杂度和冗余度都很高,在实际应用中并不理想。在此基础上M.N.DO和Vetterli[3~4]提出了一种“真正的”二维图像表示方法Contourlet(轮廓波)变换。Contourlet变换以图像中轮廓线段为固定基表示图像信息,继承了小波变换良好的时频特性,可以更好地捕捉到二维图像中的几何信息,是一种更优的二维图像表示方式。目前Contourlet变换已经被应用在图像去噪、图像增强、图像压缩等多个领域,并显示出相当的优越性。
基于小波变换的图像去噪算法的主要是针对变换后的小波系数进行相应修正,再使用修正后的系数重构图像从而达到降低图像噪声的目的。目前主要有阈值法,相关系数法,模极大值法[5]等,其中阈值法由于具有处理简单,计算量相对较小等优点得以广泛运用,而阈值法的关键就在于系数分类阈值的选取。目前常用的阈值针对所有系数均使用一个统一的大小,并未考虑多尺度分解后不同层次间的差异性。
由于Contourlet变换中包含下采样等操作,因此不具有平移不变性,在使用阈值去噪时会在不连续点附近产生伪吉布斯现象。Eslami和Radha将Contourlet变换和循环平移操作相结合[6],使用经过循环平移处理后的系数进行阈值去噪,有效提高了图像效果。本文提出了一种改进的基于局部方差的自适应阈值,并结合循环平移Contourlet变换对原有去噪方法进行改进。
2Contourlet变换理论
Contourlet变换又称为塔式滤波器组(PDFB)。它主要由两层滤波器组构成:拉普拉斯塔式金字塔分解(LP)主要负责完成图像的多尺度分解,方向滤波器组(DFB)主要负责完成图像的多方向分解。
2.1拉普拉斯塔式金字塔
拉普拉斯金字塔分解可以有效地实现图像的多分辨率分解。每一层次的分解可以产生一个经过下采样的低通部分a和一个由原始图像和预测图像生成的差值图像b。如图1所示,其中H和G均为低通滤波器,负责图像的分解与合成,M为采样矩阵。
输入图像x经过低通滤波器H和下采样矩阵生成输入图像x的低通部分a,a经过上采样矩阵和低通滤波后生成一个预测图像,输入图像与其的差值为b,可以认为是输入图像的高通细节部分。LP分解可以使用每层的下采样低通信号a可循环进行下去,从而生成第n层低通部分和n个细节部分。细节部分可以用于下一步的方向滤波器分解,并根据每层的方向分解数目,分解成不同的方向子带。
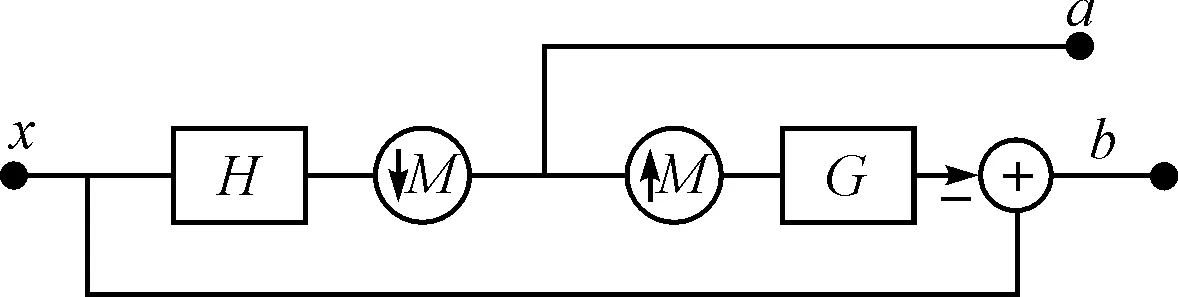
图1 LP分解
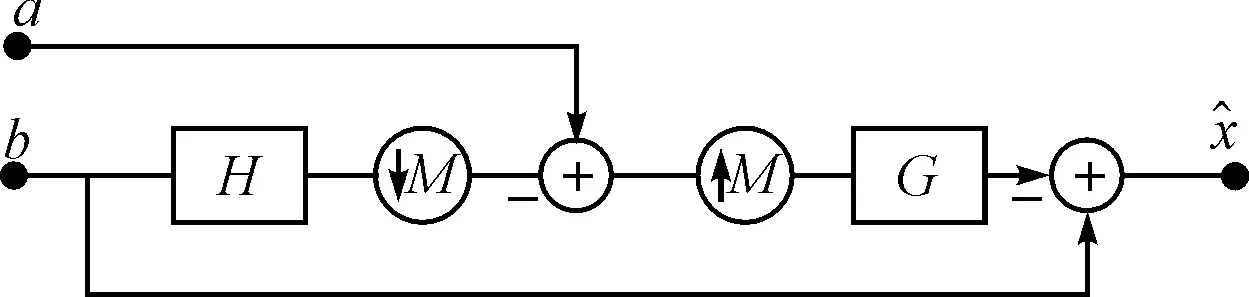
图2 LP重构
2.2方向滤波器组
方向滤波是一种能够有效扑捉图像中方向信息的图像处理手段。方向滤波器组DFB将梅花扇形滤波器组QFB的方向频率分解和重采样实现的旋转操作相结合,其中梅花扇形滤波器可以将信号分解为基本的垂直子带和水平子带,经过DFB分解后可以将上一步LP分解得到的带通图像的频谱划分为2j个起楔形频率子带[7]。图3为zoneplate图像经过三级DFB分解的子带图像。


图3 三层DFB分解
3Contourlet去噪算法
3.1阈值去噪
阈值去噪是基于小波变换的图像去噪算法之一,针对变换后的系数选定一个合理的阈值完成噪声系数和信号系数的分类,并通过相应的阈值函数完成对应的处理,使用处理后的系数重构图像来完成图像降噪的目的。
Contourlet变换是在小波变换的基础上发展而来的,所以Contourlet变换系数也可以通过阈值去噪的方式来处理。而阈值去噪的关键在于合适阈值的选取与阈值函数的合理设计。目前常用的阈值函数主要分为硬阈值函数和软阈值函数。
硬阈值函数为
(1)
软阈值函数为
(2)

阈值去噪的另一个关键问题在于合适的阈值选取,合适阈值的选取直接关系到图像去噪效果的好坏,过大或过小的阈值都会对去噪处理产生负面影响。过大的阈值把图像中有用的细节信息也全部归零,导致重构后的图像过于平滑,造成图像细节部分的模糊;过小的阈值并不能有效的去除噪声,将噪声系数和图像能量系数同时保留下来,导致重构后的图像去噪效果并不明显。
Chang在假设小波系数服从广义高斯分布的情况下,通过使贝叶斯风险最小得出了系数的贝叶斯阈值[9]:
(3)
其中σn为噪声标准差,σc为图像信号标准差,噪声标准差由中值估计法得来:
σn=Median(|coh|)/0.6745
(4)
3.2循环平移
Contourlet变换同小波变换一样不具有平移不变性,在直接使用阈值去噪后,图像对于人眼的视觉效果会受到一定影响。经过下采样后,图像信号的特征点和Contourlet基特征并不能完全匹配,所以在阈值去噪的过程中会在信号的不连续点(边缘和纹理)附近产生伪吉布斯现象[10],导致图像失真。
使用循环平移(Cycle-Spinning)操作可以有效地改善这种现象。可以对平移后的图像信号进行去噪,再将处理后的图像信号进行反向平移来避免伪吉布斯现象。平移k步操作如下公式所示,其中M,N分别为图像长宽。
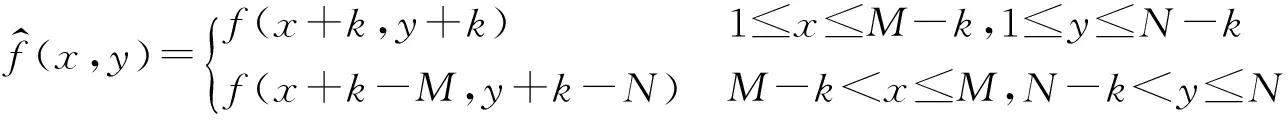
(5)
------------------------------
但是当信号包含多个不连续点时,对于某一个不连续点的最佳平移量对于其他不连续点可能效果很差。为此可以在一定范围内做循环平移,再对平移后的结果进行叠加平均。在本文算法中,将输入图像的分解尺度设定为循环平移的最大步数,从最低平移步数开始,对每一级平移后的输入图像进行Contourlet变换,并针对系数完成阈值去噪处理,对重构后的图像进行反向平移获取处理图像,最后将所有平移处理的图像叠加后求均值得到最终的去噪图像。
3.3基于局部方差的自适应阈值
图像经过Contourlet分解后,主要细节信息集中在一部分有限的子带系数中,噪声则会均匀的分布在不同方向子带中。对于一幅细节轮廓较为丰富的图像,图像中不同方向的细节信息分布有一定差别。Lena图像经Contourlet分解后最高尺度的方向子带系数分布如图4所示。
可以在图4中直观的看出,方向子带系数模值的大小与分布直观地体现了图像轮廓细节的分布,图像细节系数在子带图像中表现为边缘纹理,而噪声系数在子带图像中表现为大面积的黑色区域。可以使用局部方差来衡量某一系数属于图像细节还是噪声,局部方差是计算系数在其N*N邻域内的方差大小,方差表征了样本偏离样本均值的程度。因此,如果一个系数的局部方差值较大,可以认为该系数对应图像中的轮廓边缘信息;反之,如果该系数的局部方差值较小接近于0,可以认为该系数对应于噪声能量。
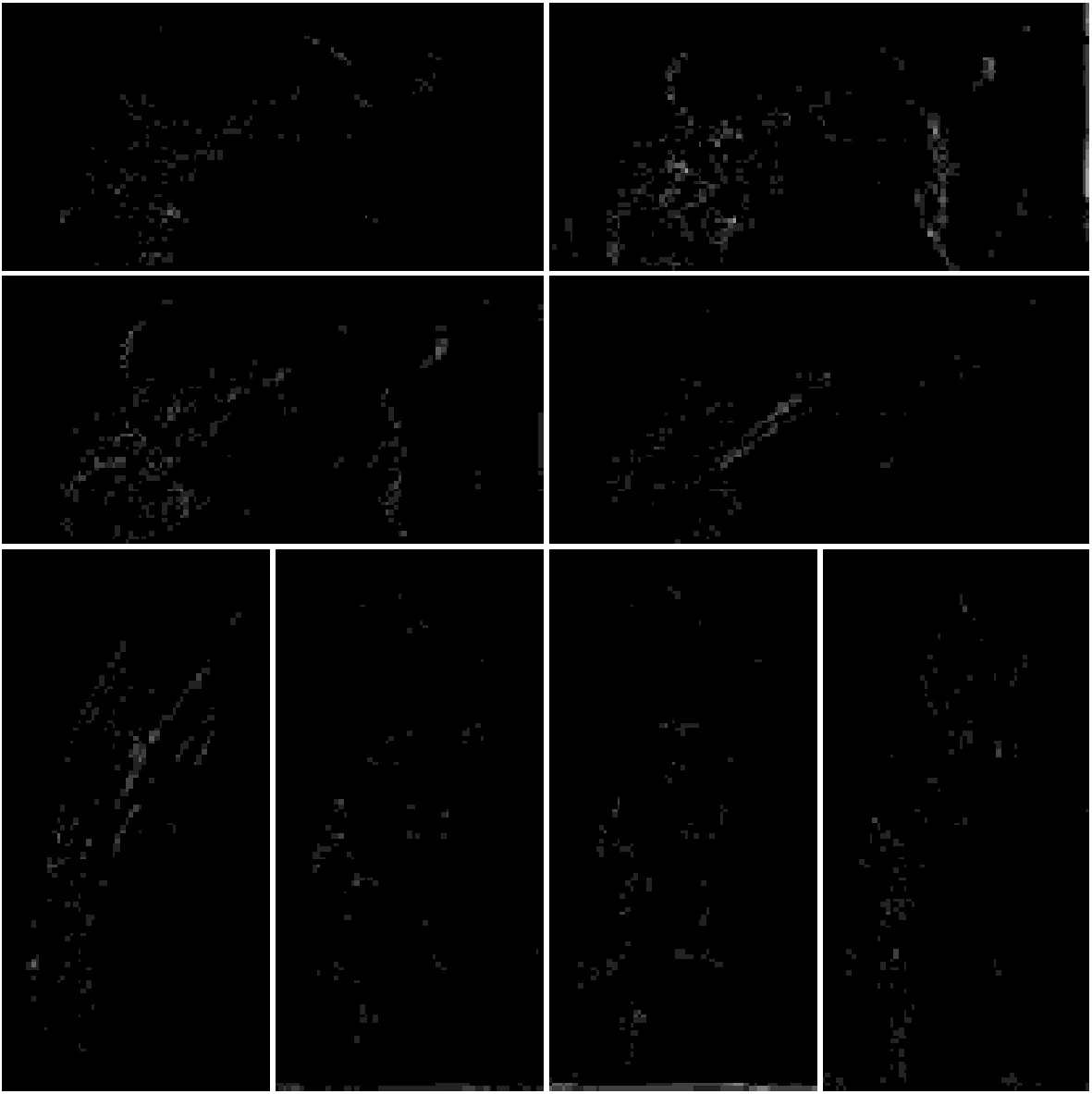
图4 系数分布
对于方向子带内任一Contourlet系数,它在3*3邻域内的局部方差计算公式为
(6)
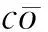
(8)
3.4本文算法
本文算法将自适应贝叶斯阈值同循环平移的Contourlet变换相结合,提出了一种改进的阈值去噪算法,算法的主要步骤如下:
1) 设置Contourlet变换基本参数,根据分解尺度设定循环平移最大步数K;
2) 根据当前平移步数k将输入图像按行平移k步,并根据分解尺度与每一尺度的方向分解数进行Contourlet分解;
3) 循环处理不同尺度下不同方向子带系数,根据式(6)计算每一方向子带系数在3*3邻域的局部方差得到子带系数的局部方差矩阵,根据式(7)归一化处理后得到调节因子矩阵;
4) 对每一个方向子带系数根据调节因子和基础阈值计算自适应阈值,其中本章算法中基础阈值选用式(3)所示的贝叶斯阈值,使用硬阈值收缩函数处理系数;
5) 使用处理后的系数重构图像,将重构图像反向平移当前步数k,获取当前重构图像fk;
6) 递增平移步数k=k+1,判断k是否大于最大步数K,如果不大于K则继续执行步骤2)~6),否则转到步骤7);
7) 对于所有得到的重构图像fk用式(9)求均值,获取去噪处理图像。
(9)
算法的具体流程如图5所示。
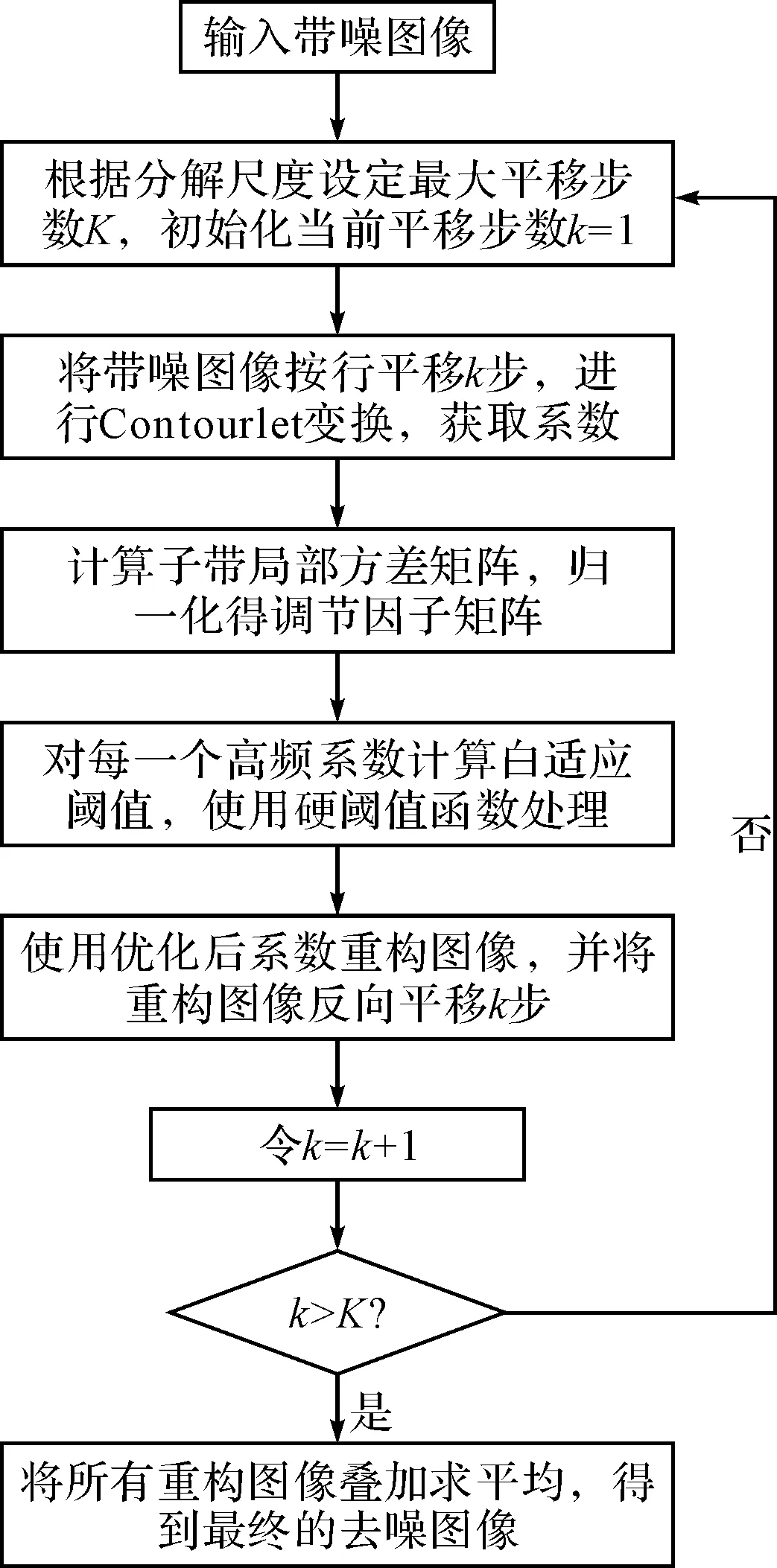
图5 算法流程
4实验结果与分析
为验证算法有效性,选取添加有不同大小的高斯白噪声的实验图像进行处理。分别选取Contourlet硬阈值去噪,循环平移Contourlet阈值去噪以及本文算法进行对比。采用峰值信噪比(PSNR)作为客观衡量标准来检验算法的性能。
使用512*512标准大小的Peppers图像,并人工添加标准差为20的高斯白噪声,分别运用Contourlet软硬阈值去噪与本文算法做去噪处理,其中Contourlet分解尺度为4,每一层的方向数分别为2,3,3,4。所得图像与原噪声图像的对比如图6所示。
由图6可以看出,Contourlet阈值去噪对于噪声图像的处理有着不错的效果,硬阈值去噪相比于软阈值去噪可以获得更好的PSNR,对噪声的去除效果也更加明显,但是在图像的个别部分产生突变现象,影响了图像的视觉效果,而本文算法相对于常规的阈值去噪方法,可以获得更高的PSNR值,对噪声的去除更加有效,同时较大程度的保留了图像中的边缘与轮廓信息。表1为针对含有不同大小噪声的图像进行处理后的结果对比,可以看出相对于其他算法,在不同的噪声等级下,本文算法均可以获得较好的去噪效果。


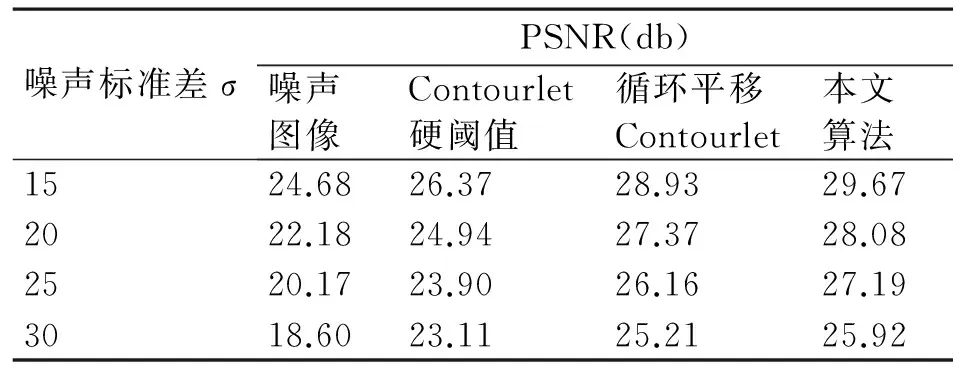
噪声标准差σPSNR(db)噪声图像Contourlet硬阈值循环平移Contourlet本文算法1524.6826.3728.9329.672022.1824.9427.3728.082520.1723.9026.1627.193018.6023.1125.2125.92
5结语
本文研究了一种基于Contourlet变换的图像阈值去噪方法。根据Contourlet系数不同层次的特点,使用了基于局部方差的自适应阈值,同时在原有Contourlet变换基础上,引入了循环平移方法,改善了视觉效果。经过实验对比,相比于常用的软硬阈值去噪算法,本文算法去噪效果更加显著,同时可以有效地保留图像的细节信息。
参 考 文 献
[1] Mink N Do, Martin Vetterli. The finite Ridgelet transform for image representation[J]. IEEE Transactions on Image Processing,2002,1(12):16-28.
[2] J-L Starck, E J Candes, D L Donoho. The curvelet transform for image de-noising[J]. IEEE Transactions on Image Processing,2002,6(11):670-874.
[3] Do M N, Vetterli M. The Contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing,2005,14(12):2091-2106.
[4] Do M N, Vetterli M. Contourlets: a directional multi-resolution image representation[C]//IEEE International Conference on Image Processing. Rochester, NY: IEEE,2002:357-360.
[5] 杨帆,赵瑞珍,胡绍海.基于Contourlet系数相关特性的自适应图像去噪算法[J].光学学报,2009,29(2):357-361.YANG Fan, ZHAO Ruizhen, HU Shaohai. Adaptive image denoising algorithm based on Contourlet coefficient correlation[J]. Journal of Optics,2009,29(2):47-49.
[6] R. Eslami, H. Radha. Translation-Invariant Contourlet Transform and Its Application to Image Denoising[J]. IEEE Transactions on Image Processing,2006,15(11):3362-3367.
[7] 焦李成,等.图像多尺度几何分析[M].西安:西安电子科技大学出版社,2008:20-326.
JIAO Licheng. Multiscale geometric analysis of images[M]. Xi’an: Xi’an Electronic and Science University Press,2008:20-326.
[8] Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory,1995,41(3):613-627.
[9] Chang S G, Yu B, Vetterli M. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. IEEE Transactions on Image Processing,2000,9(9):1522-1531.
[10] 陈志刚,尹福昌.基于Contourlet变换的遥感图像增强算法[J].光学精密工程,2008,16(10):35-37.CHEN Zhigang, YIN Fuchang. Remote sensing image enhancement algorithm based on Contourlet transform[J]. Optics and Precision Engineering,2008,16(10):35-37.
Adaptive Threshold-Denoising Method of Image Based on Contourlet Transform
LI HuiJIANG Chao
(The 28th Research Institute of China Electronics Group Corporation, Nanjing210007)
AbstractA class of image denoising method based contourlet transform is studied. Contourlet transform is an efficient method for image representation, it has better performance at portray the texture information of the image. According to the different characteristics of Contourlet coefficient, a denoising algorithm is studied based on adaptive threshold and the cycle-spinning Contourlet transform. Experiments on image denoising shows that, compared to the Contourlet soft-threshold and Contourlet hard-threshold, the algorithm in this paper can keep more image detail and improve the PSNR.
Key WordsContourlet transform, denoising, Bayes threshold
收稿日期:2015年12月12日,修回日期:2016年1月23日
作者简介:李辉,男,硕士,工程师,研究方向:应用软件开发。姜超,男,硕士,助理工程师,研究方向:应用软件开发。
中图分类号TP391
DOI:10.3969/j.issn.1672-9722.2016.06.038
