物流配送过程中的3L-CVRP问题及其遗传算法研究

王凤丽　毕　然　王家敏　姜　滨

(山东商业职业技术学院国家农产品现代物流工程技术研究中心　济南　250103)

物流配送过程中的3L-CVRP问题及其遗传算法研究

王凤丽毕然王家敏姜滨

(山东商业职业技术学院国家农产品现代物流工程技术研究中心济南250103)

摘要针对物流配送中多种货物的装箱及路径优化问题,提出了一种带有容量约束的三维装箱和车辆路径问题的求解方案。在考虑装箱过程中车辆载重、物品性质和体积等约束条件的基础上进行模型构建,并采用遗传算法对模型进行了求解。通过10组实验数据对所构建的模型进行测试分析,其中实验结果的最优解即目标函数最优值是104.195,运行时间为125312ms,测试结果表明该模型算法能够有效提高车辆的使用效率,降低物流配送成本。

关键词三维装箱; 路径选择; 遗传算法; 多约束条件

Class NumberTP311.52

1引言

随着物流系统集约化、一体化发展,需要将配送作业的各个环节综合起来进行系统化考虑[1]。货物配装及配送路径作为配送的基础重要环节,在物流成本控制方面起着至关重要作用。一方面,货物配装问题解决得好坏直接关系到车辆空间、载重利用率,并且货物配装问题又是货物运输中的安全问题之一;另一方面,配送路径优化一直是配送企业节约运送成本的一个着眼点。因此,车辆路径问题(Vehicle Routing Problem,VRP)如何设计合理、有效的车辆行驶路线,以达到减少车辆使用数量和行驶路线长度的目的;装箱问题(Container Loading Problem,CLP)如何设计高质量的装箱方案,减少车辆的使用数量,从而提高运输工具的利用率,都是降低物流成本要考虑的因素。带有容量约束的三维装箱和车辆路径问题(Three-Dimensional Loading Capacitated Vehicle Routing Problem,3L-CVRP)结合了两个著名的NP-hard问题,即车辆路径问题(Vehicle Routing Problem,VRP)和三维装箱问题(Three-Dimensional Packing Problem,3DPP),它从系统层面上综合考虑路径优化和合理装箱问题,对降低物流配送成本、提高物流企业竞争力有着重要的意义。

物流装载配送过程是通过对一些大小不同的规则立方体在三维规则箱体内进行合理放置,并在进行三维空间位置放置的同时考虑配送路径优化,从而达到控制物流配送成本的目的。所以,物流装箱配送问题是3L-CVRP问题。由于3L-CVRP是NP-Hard问题,国内外学者大都采用现代启发式算法对其进行研究。Michel Gendreau等人提出了采用双层禁忌搜索算法解决3L-CVRP问题[2];Guenther Fuellerer等提出蚁群算法,使用了一般化了的节约算法,在节约算法中引入信息素以及反映装箱好坏的评价函数,再通过局部搜索进一步优化解[3];David Mester介绍了一种基于多参数的进化算法用于解决3L-CVRP问题,并对六个实际应用问题进行了测试[4];Damon、Teodor Gabriel Crainic等人采用现代启发式算法对其进行了研究[7,11]。在目前报道的文献中,主要集中在对方法及实验室数据进行讨论,对于考虑物品的可选放置方向、重心、承重能力等因素较少。特别是运用遗传算法解决3L-CVRP问题的研究还不多。

本文通过调研及文献分析,对物流配送过程中的3L-CVRP进行了描述,分析了影响物流配送过程的影响因素,找出了本研究的主要约束条件,构建适用于物流配送过程的3L-CVRP模型,针对3L-CVRP特点,设计了自然数编码的遗传算法。最后,结合实例验证了模型和算法的可行性。

2问题描述

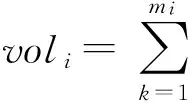
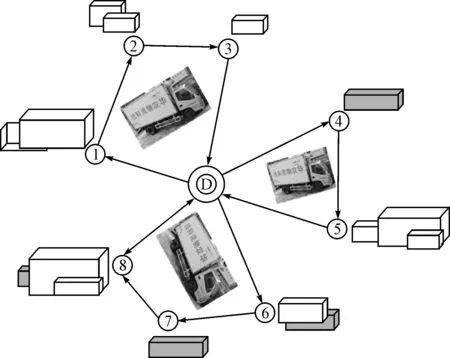
图1　3L-CVRP的示意图

配送成本占物流成本较大的比重,从而尽可能地降低配送成本对物流企业增加其竞争力有着重要的作用。在配送过程中物流企业希望找到一种在满足客户要求下的有效配送方法。该方法要求车辆在装卸过程中货物间没有浪费和倒箱现象;在运输过程中较少存在迂回运输现象。因此,与此相对应的3L-CVRP求解目标是找到装箱和路径结合的方案,既要保证车辆装载率,又要保证配送路程较短,从而尽可能地降低配送成本。在配送过程中,为了保证客户的需求,要求所有客户的订单都要被处理;为了保证客户交接货物时的方便性,要求每个客户只由一辆车服务,即由一个客户要求的所有物品需要有一辆车来完成,不能分批配送货物;当货车按照顺序服务客户的时候,必须能够顺利卸下其货物,不可产生多次装卸现象,卸货时货物只能向上方向移动,要卸的货物不能被其它货物压着,其前面不能被其他货物挡住;为了保证货物的质量及运输安全,需要考虑其容量情况,应尽量减小物品在车厢内的晃动;此外,还应该考虑产品特性,有些产品不倒置、不侧放、运输车辆需预留一定的空调出风口。因此,产品的3L-CVRP一般情况下需要满足以下约束条件:

1) 订单完整性约束:一个客户要求的所有物品需要有一辆车来完成,不能分批配送货物;

2) 正交放置:要求物品在车厢内正交放置,即物品的边楞与车的长宽高方向平行;

3) 容积约束:车中所有放置的物品不能超出车辆边界,货物的总体积不能超过车厢的体积;

4) 重量约束:为了保证行车安全,车中所有放置的物品重量不能超过车辆的载重;

5) 旋转约束:考虑到货物品的特殊性,有些不能倒置只能在水平平面内做90°旋转;

6) 易碎性约束:如图3中标识货物,灰色标识为易碎品,文中1表示是易碎品,0表示非易碎品。易碎物品可放在易碎物品上面,易碎物品可放在非易碎物品上面,但非易碎品不能放在易碎品上面;

7) 平衡性约束:只有当支撑面积与底面积的比值超过一个给定的阈值比θ时才允许摆放;

8) 先进后出约束:当货车按照顺序服务客户的时候,必须能够顺利卸下其货物,卸货时货物只能延垂直方向移动,要卸的货物不能被其它货物压着,其前面不能被其他货物挡住。

3模型构建

在物流配送过程中,既要保证满足客户的需求又要尽可能地降低成本。本文考虑的配送成本包括车辆的使用成本和车辆的运输成本,总的目标是在满足约束的情况下运输的成本最少。3L-CVRP是在考虑货物特性及满足其上述的约束条件下,从配送成本考虑,将定单汇集起来,通过合理的配载、拼箱,实现农产品的多频次、少批量的配送服务;同时,应减少运输中的不合理现象(迂回运输、重复运输)。在保证货物质量和运输安全的情况下,客户需求订单通过合理的配载使得车辆的使用量和运输距离最短是合理的配送过程。因此,笔者建立了以运输过程中的总成本最少的目标的模型:

(1)

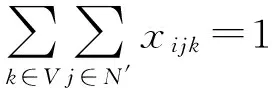
(2)

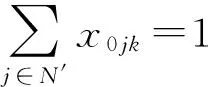
(3)

(4)

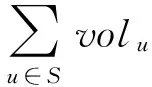
(5)

(6)

(7)

xijk∈{0,1}

(8)

其中,α表示配送成本中可变成本的比例系数;P、Q分别表示配送成本中可变成本、固定成本;V表示车辆的容量;D表示车辆的载重;Cij表示从i地到j地的直线距离;xijk为0-1变量,值为1时表示车辆k从i地到j地。

在上述模型中,式(1)为目标函数,即要求在配送总成本(车辆的使用固定成本,配送距离产生的可变的成本)最小;式(2)和式(3)为一个顾客的货物都是由一辆车来完成,从而保证了订单的完整性;式(4)和式(5)为车辆体积约束;式(6)和式(7)为车辆体积约束;式(8)表示车辆k从i地到j地,则取xijk为1,车辆没有k从i地到j地,则取xijk为0。

43L-CVRP模型遗传算法设计

4.1遗传算法概述

20世纪60年代,美国J. Hold教授从生物遗传学“物竞天择,适者生存”的自然规律中得到灵感和启迪,创立了基于自然选择的编程技术-遗传算法(Genetic Algorithms)[12]。遗传算法是一种迭代搜索算法,通过构建染色体、种群选择、染色体交叉和变异等过程,实现自适应随机搜索,具备优良的鲁棒性和潜在的并行计算机制,能够以很大的概率找到问题的最优解,因此,遗传算法在求解3L-CVRP等NP-hard问题方面具有很大的优势。

4.2遗传算法设计

遗传算法是根据问题的目标函数构造一个适值函数,以群体中所有个体为操作对象,对染色体构成的种群进行评价、遗传运算、选择经过多代繁殖,获得适应值最好的个体作为问题的最优解。因此,需要构造染色体色体(解)、确定适应度函数以及主要操作算子,针对3L-CVRP问题,具体算法设计如下。

4.2.1染色体编码

染色体编码是把物流配送问题的可行解从现实中转换到遗传算法所能处理的搜索解空间。在遗传算法过程中,种群中的每个个体都是由基因构成的,要染色体与待求解的问题进行对应,就需要对基因进行正确的编码。在配送过程中,订单中的货物的顺序、位置、放置方式和订单的顺序确定了整个的装载过程和路径。故与之相对应3L-CVRP的染色体中应包含车辆、订单、货物、货物放置方式信息,宜采用自然数编码,我们用集合表示一个染色体{a1-a2…,b1-b2…,c1-c2…;ck-ck+1…,d1-d2…}。集合中的ai表示代表订单编号,bi代表ai订单所在的车辆编号,ci代表所有订单中货物顺序订单之间用分号隔开,di表示与ci位置序号一致的货箱的方置方向。如两辆车配送四个订单的染色体为:{1-3-2-4,0-1-1-2,2-1;3-4;5-6;7-8,0-1-2-1-2-3-5-4}。表示1号订单中的以2号货物以水平侧放,1号竖直放置装入0号车。

4.2.2种群初始化及适应度评价

种群初始解为随机产生的自然数序列。对n个订单k车的配送过程编码的过程如下:在ai位置上随机产生n个订单序列;在bi位置上产生n个在[1,k](k为车辆的数目)范围内的随机序列;在ci位置上随机产生订单中货物顺序,订单间用分号隔开;di位置随机产生在[0,5]范围内货箱的方置方向序列。如此反复,直到产生满足种群数目。

适应度评价:在遗传算法中使用适值函数来表征种群中每个给以对其生存环境的适应能力,适值函数的形式直接决定着群体的进化行为。配送成本越小越有利于物流企业控制成本,增强其竞争力。为了能够直接将适值函数与群体中的个体优劣相联系,在此采用适应度函数是目标函数的倒数,由此可见函数值越小的染色体越优良。

4.2.3选择操作

在遗传算法中自然选择规律的体现就是以适应值的大小决定的概率分布进行选择,最常用的选择策略是正比选择策略。即每个个体被选中进行遗传运算的概率为该个体的适应值和群体中所有个体适应值总和的比例。对于个体i,设其目标函数值为Fi,种群规模为NP,则该个体被选择概率Pi可表示为

(9)

得到选择概率后,采用轮盘赌来实现选择操作。令

PP0=0

(10)

(11)

每次转轮时,随机产生ξk∈U(0,1),当PPi-1≤ξk≤PPi,则选择个体i,共转轮NP次。

4.2.4遗传操作

1) 交叉操作:对于3L-CVRP问题,如果单纯地使用一般的交叉算子往往会使一些优良的子串被破坏,并且在染色体间交叉时,无法产生有效的个体。在此采用一种有效的双切点交叉算子,对于两个选定的染色体随机选取两个切点,交换两个切点间的子串。对于染色体A、B在切点9和14上进行双切点交叉,得到染色体C、D,如下所示:

A: 1-3-2-4,2-1-0-1,2-1;3-4;

5-6;7-8,0-1-2-1-2-3-5-4;

B:1-3-2-4,0-1-1-2,3-4;2-1;

5-6;7-8,0-1-2-1-2-3-5-4;

C: 1-3-2-4,0-1-1-1,2-1;3-4;

5-6;7-8,0-1-2-1-2-3-5-4;

D: 1-3-2-4,2-1-0-2,3-4;2-1;

5-6;7-8,0-1-2-1-2-3-5-4。

在交叉运算过程中会遇到不合法的编码,例如选择的切点为17和21,经交叉后,后代的编码不合法。对于这种情况,本文采用了部分映射交叉修复策略。

2) 变异操作:在种群中,变异是按照变异概率任选若干基因位改变其位值改变基因的过程。通过变异,染色体产生随机变化,可以提供初始种群中不含有的基因或选择过程中丢失的基因。可以通过变异操作控制车辆的使用信息。变异概率一般为一个较小的数,在(0,0.05)范围内。

重复上述步骤,根据遗传算法迭代次数或种群的收敛停止循环,输出最终结果。

5算例仿真

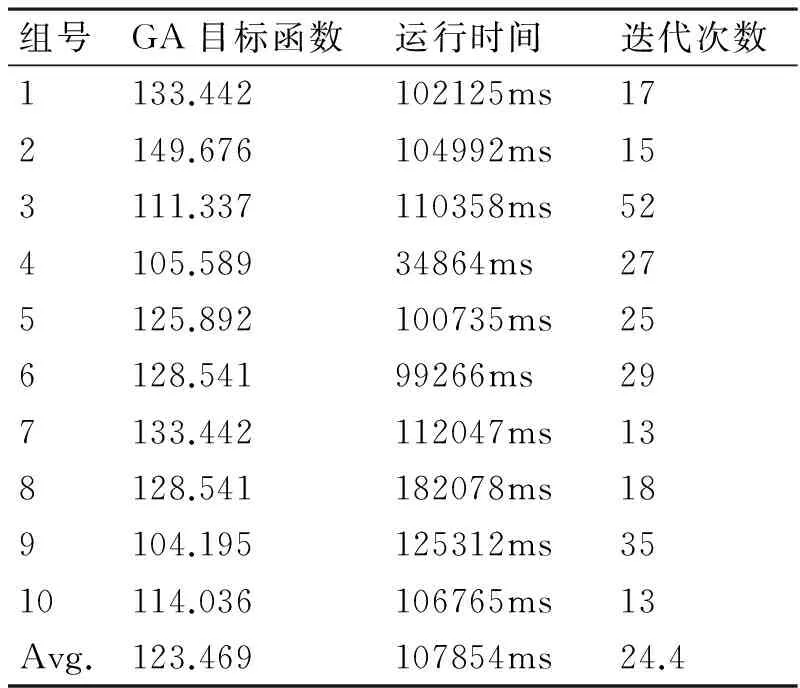
表1　遗传算法测试结果

在Pentium(R)4,CPU2.8GHz,1G内存的计算机上,WindowsXP系统环境下采用面向对象的JAVA语言,对文章中描述的算法进行系统实现。本文采用http://www.or.deis.unibo.it/research_pages/ORinstances/ORinstances.htm网站中提供的货物数据信息对算法进行测试模拟。其余数据根据与公司工作人员的讨论确定固定成本为30(无量纲),可变成本为6,两者间的比例为0.65∶0.35。遗传算法的种群大小为20,遗传操作的交叉率为0.85,变异率为0.05,迭代次数最高限阈值为200次。系统的运行时间阈值为270000ms,对网站上3L-CVRP数据进行了10组测试。测试结果如表1所示。经过遗传算法计算,最优目标函数值为104.195,运行时间为125312ms,迭代次数为35次。平均的目标函数值、系统运行时间及平均迭代次数分别为123.469、107854ms、24.4次。

6结语

1) 本文针对物流配送问题,提出了采用遗传算法对货箱装载和路径进行优化处理的方法,建立了相应的数学模型并详细描述了遗传算法的构造过程。

2) 采用双切点交叉方式对配送过程中的染色体进行了自然数编码,实现了染色体编码与现实配送过程的一一映射,并在交叉过程中对不合法的染色体进行了部分映射交叉修复。

3) 由于产品物流配送过程中的复杂性,如何将产品配送过程中其他因素如带有时间窗约束的配送问题等将是下一步工作重点。

参 考 文 献

[1] 周向明,钱建平,杨信廷,等.农产品物流配送过程信息技术应用研究进展[J].中国农学通报,2010,26(8):323-327.ZHOU Xiangming, QIAN Jianping, YANG Xinting, et al. Review the application of information technology in agricultural products logistics and distribution[J]. Chinese Agricultural Science Bulletin,2010,26(8):323-327.

[2] Michel Gendreau, Manuel Iori, Gilbert Laporte, S.M. A Tabu Search Algorithm for a Routing and Container Loading Problem[J]. Transportation Science,2006,40(3):342-350.

[3] Guenther Fuellerer, Karl F. Doerner, Richard F. Hartl, M.I. metaheuristics for vehicle routing problems with three-dimensional loading constraints[J]. European Journal of Operational Research,2001(201):751-759.

[4] David Mester, Olli Braysy, W.D. a multi-parametric evolution strategies algorithm for vehicle routing problems[J]. Expert Systems with Applications,2007(32):508-517.

[5] Damon, E.W. the split delivery vehicle routing problem with minimum delivery amounts[J]. Transportation Research Part E,2010:1-5.

[6] Teodor Gabriel Crainic, Guido Perboli, Roberto Tadei. ts2pack: a two-level tabu search for the three-dimensional bin packing problem[J]. European Journal of Operational Research,2009(195):744-760.

[7] Bortfeldt A. A hybrid algorithm for the capacitated vehicle routing problem with three-dimensional loading constraints[J]. Computers & Operations Research,2012,39(9):2248-2257.

[8] Zhu Wenbin, Qin Hu, et al. A two-stage tabu search algorithm with enhanced packing heuristics for the 3L-CVRP and M3L-CVRP[J]. Computers & Operations Research,2012,39(9):2178-2195.

[9] Junqueira L, Oliveira J F, Carravilla M A, et al. An optimization model for the vehicle routing problem with practical three-dimensional loading constraints[J]. International Transactions in Operational Research,2013,20(5):645-666.

[10] Ruan Qingfang, Zhang Zhengqian, Miao Lixin, et al. A hybrid approach for the vehicle routing problem with three-dimensional loading constraints[J]. Computers & Operations Research,2013,40(6):1579-1589.

[11] Tao Yi, Wang Fang. An effective tabu search approach with improved loading algorithms for the 3L-CVRP[J]. Computers & Operations Research,2015,55:127-140.

[12] 孙棣华,涂平,彭光含,等.基于遗传算法的单车运输配载研究[J].计算机仿真,2008,25(3):285-288.

SUN Dihua, TU Ping, PENG Guanghan, et al. Study on Single Truck Loading of Transportation Based on Genetic Algorithm[J]. Computer Simulation,2008,25(3):285-288.

Genetic Algorithm for Three Dimensional Loading Capacitated Vehicle Routing Problem in Logistics Distribution

WANG FengliBI RanWANG JiaminJIANG Bin

(National Agricultural Modern Logistics Engineering Technology Research Center,Shandong Institute of Commerce and Technology, Jinan250103)

AbstractIn order to optimize product distribution and save logistics cost, this paper addresses an approach for three-dimensional loading capacitated vehicle routing problem including three-dimensional loading problem and vehicle routing problem. Given the multiple constraints, such as vehicle weight, item properties, item volume, etc, the model is built based on genetic algorithm. The algorithm is experimentally evaluated on instances adopted from 10 instances. It can be seen from the running result that the running time is 125312ms and the best value of objective function is 104.195 which indicates that the algorithm can effectively optimize logistics cost.

Key Wordsthree dimensional loading, vehicle routing, genetic algorithm, multi-constraint

收稿日期:2015年12月7日,修回日期:2016年1月19日

基金项目:山东省自主创新专项-黄河三角洲特色农产品电子商务平台建设与示范(编号:2013CXC90303)资助。

作者简介:王凤丽,女,硕士,研究方向:农产品物流配送。毕然,男,硕士,工程师,研究方向:农业信息化关键技术。王家敏,男,硕士,副教授,研究方向:农业信息化及农产品质量安全控制。姜滨,男,助理工程师,研究方向:农业信息化及农产品物流配送管理。

中图分类号TP311.52

DOI:10.3969/j.issn.1672-9722.2016.06.007