扑翼飞行器非定常气动特性研究

王建领, 何广平, 狄杰建

(北方工业大学 机械与材料工程学院, 北京 100041)

扑翼飞行器非定常气动特性研究

王建领, 何广平, 狄杰建

(北方工业大学 机械与材料工程学院, 北京 100041)

摘要:为了研究复杂的非定常运动状态下扑翼飞行器翅翼的气动特性,针对自行研制的一种仿鸟扑翼飞行器建立了翅翼二维非定常空气动力学模型。基于该模型,通过用MATLAB编制计算升力系数和推力系数的程序,计算并分析了各运动参数对升力和推力特性的影响。结果表明,相位差对推力系数的影响较大,而升力系数随迎角的变化较快。

关键词:仿生扑翼飞行器; 非定常空气动力学; 升力系数; 推力系数

0引言

近年来,仿生扑翼飞行器因其尺寸小、机动灵活、携带方便、低成本、隐蔽性好以及可执行多种任务等优点,已经成为国内外研究的热点。在复杂的非定常运动状态下对翅翼进行气动力学性能研究和分析,对设计性能优越的扑翼飞行器具有十分重要的意义。国内外对此已进行了多方面的研究:Weis-Fogh[1]提出了昆虫产生高升力的机制——Weis-Fogh机制;Sun等[2]采用Navier-Stokes方程分析了昆虫在非定常运动状态下的气动力特性;Lin等[3]采用简化后的N-S方程(即Euler方程)模拟了翅翼在非定场状态下的气动特性。但是直接求解上述方程,计算量均特别庞大。

本文在准定常模型(Quasi-steady)[4-5]的基础上,通过考虑流场的非定常特性,采用MATLAB软件编制计算升力系数和推力系数的程序。该程序只需输入运动的类型以及翅翼运动参数(如拍动振幅、俯仰角和相位差等),即可得到升力系数和推力系数等参数,具有快速、高效等特点,有利于模拟非定常条件下各个运动参数对扑翼飞行器气动特性的影响,为扑翼飞行器的进一步研究和设计提供参考。

1研究对象

目前研制的扑翼飞行器按尺寸可以分为仿鸟扑翼飞行器和仿昆虫扑翼飞行器两种类型。由于仿鸟扑翼飞行器技术相对比较成熟,并且可以承载一定的载荷,所以本文研究对象为自行研制的仿鸟扑翼飞行器(见图1)。由于翅翼薄膜的厚度相对弦长可以忽略,翅翼可以简化成无厚度膜板,因此本文研究对象为无厚度刚性薄板翅翼。

图1　扑翼飞行器Fig.1　Flapping-wing aircraft

2运动模型及计算方法

2.1升力系数和推力系数

由于升力系数CL和推力系数CT对评价扑翼飞行器性能具有重要的意义。本文研究的目的是建立输入运动参数与输出力系数(CL,CT)之间的关系。根据文献[6]提出的方法,在非定常条件下,作用在机翼上的非定常力可分为准定常力Ls、惯性力Li、诱导力Lw和前缘吸力Px,其作用方向如图2所示。图中:V∞为大气来流速度。

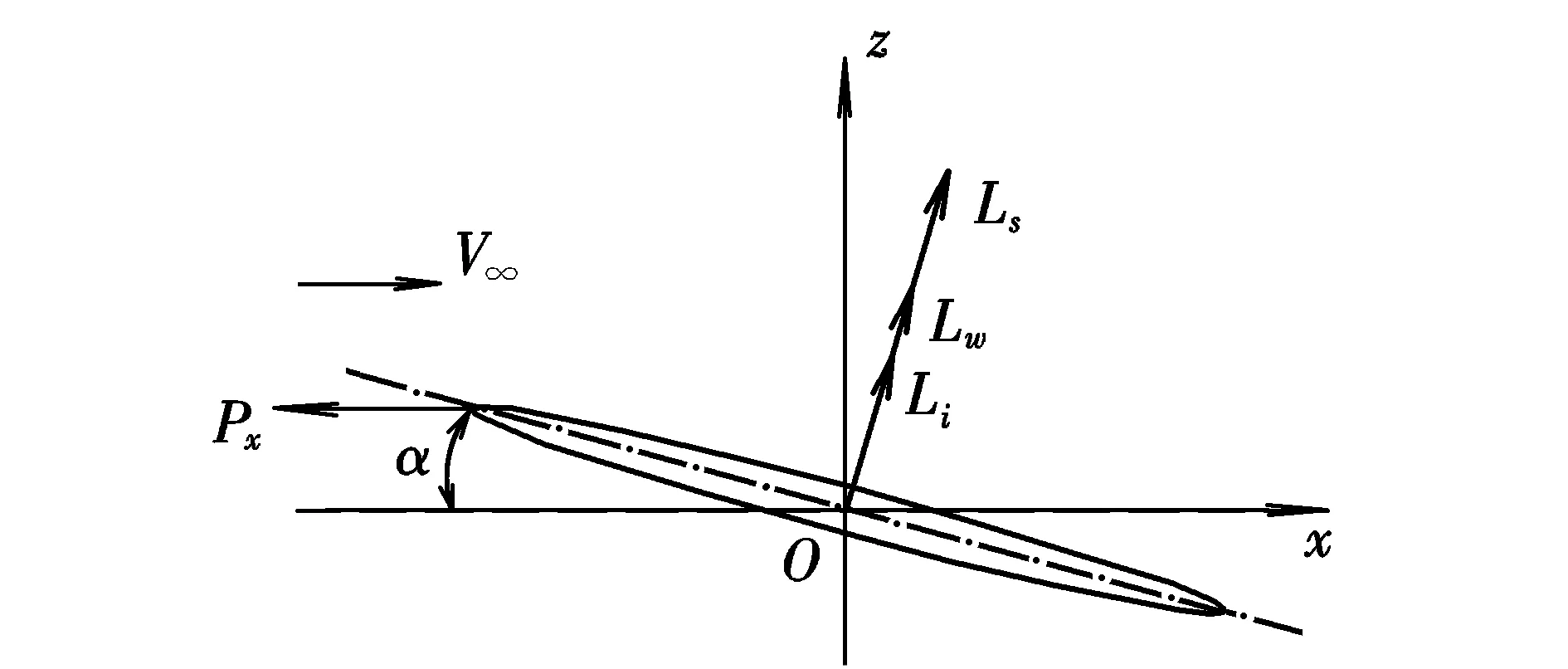
图2　非定常条件下机翼受力图Fig.2　Force of the wing under the unsteady condition

由于机翼的升力和推力分别垂直和平行于来流方向,因此,由图2可得机翼所受升力和推力为:

(1)

(2)

转化为无量纲的输出力系数为:

(3)

(4)

式中:CLs为准定常力系数;CLi为惯性力系数;CLw为诱导力系数;CPx为前缘吸力系数。几种力的计算如下:

(1)准定常力。在定常和非粘性流动条件下,根据Kutta-Joukowski定理[7]和作用在机翼上的合力垂直于大气来流方向,得出t时刻的准定常力为:

(5)

式中：Γ0(t)为t时刻机翼的定常环量。根据式(5)可推出准定常力系数为:

(6)

式中:τ为无量纲时间;c为机翼弦长;t为时间。

根据Kelvin定律[7]知,Wa(τ)由束缚环量产生,方向垂直于弦长的分速度,其大小可根据Kelvin定律和薄翼型理论[7]得出:

(7)

对式(7)求导可得:

(8)

式(7)和式(8)用于计算惯性力、诱导力和前缘吸力,同时把输入运动参数与CL和CT联系起来。

(2)惯性力。当翅翼在一个周期内上下扑动时,由于不断增加气流的质量,环绕在机翼周围的流体会产生惯性效应,从而产生惯性力。其无量纲系数表达式为:

(9)

(3)诱导力。由Kelvin定律可知,任意时刻整个流场的环量之和Γ为常数,即dΓ/dt=0,因此当机翼环量之和发生变化时,尾流区环量也会发生变化,两者的环量变化量大小相等,符号相反,以保持总环量不变。这种变化会导致翅翼上产生一个非定常力,即机翼后缘诱导力,方向垂直于翅翼的弦线。其无量纲系数表达式为:

(10)

(4)前缘吸力。根据薄板理论以及Kutta-Joukowski定理,在机翼的前缘作用了一种力,即前缘吸力。该力的方向与来流速度方向平行,其无量纲系数表达式为:

(11)

2.2动力学参数分析算法

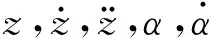
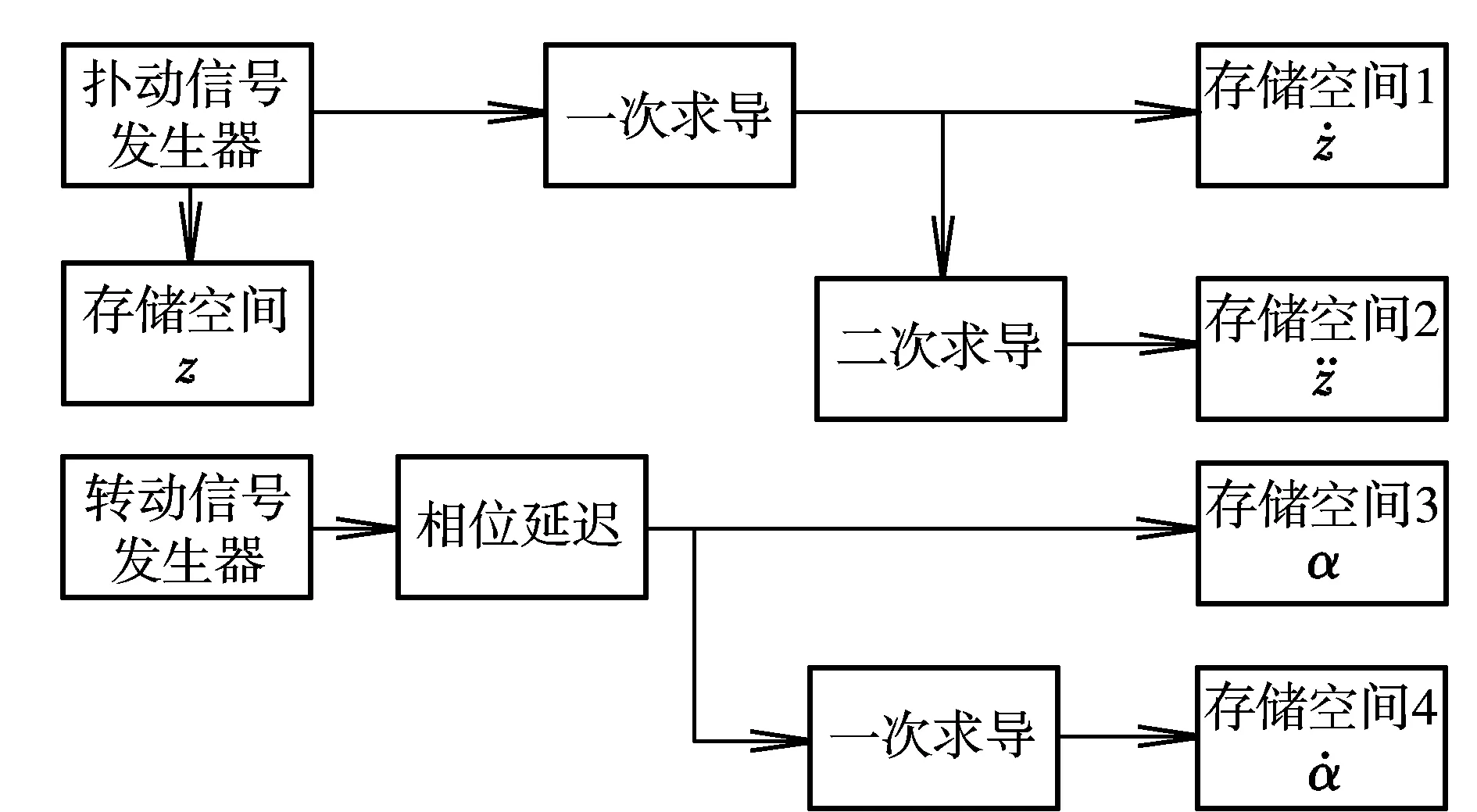
图的仿真计算模型图Fig.3　Simulation model to calculate the

3扑翼模拟计算结果与分析

3.1算法理论验证

为了验证本文程序算法的可行性,机翼运动参数的取值与文献[8]相应参数完全一致,取:k=l=0.4,αmax=2°,φ=180°,V∞=16.5 m/s。其中:k为拍动减缩频率;l为俯仰减缩频率;αmax为最大俯仰角;φ为拍动与俯仰运动的相位差。计算得到CL随无量纲时间τ的变化曲线如图4所示。从图中可以看出,在一定范围内两种方法的计算结果吻合得很好,验证了该方法的可行性。

图4　升力系数随无量纲时间的变化Fig.4　Change of lift coefficient with 　the non-dimensional time

3.2运动参数对CL和CT的影响

使用该非定常算法对本文扑翼飞行器进行分析,飞行器主要尺寸及运动参数为:翼展b=686 mm;弦长c=200 mm;扑动频率f1=5 Hz;俯仰频率f2=5 Hz;V∞=1 m/s;两者的减缩频率k=f1c/(2V∞)=0.5,l=f2c/(2V∞)=0.5;相位差φ=0°;翅翼运动规律为:θ(t)=30°sin(10πt),α(t)=20°sin(10πt)。

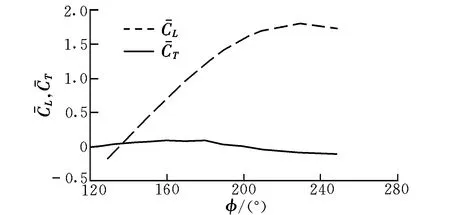
图5　平均输出力系数随相位差的变化Fig.5　Change of average output force coefficientwith phase difference

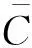
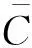
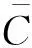
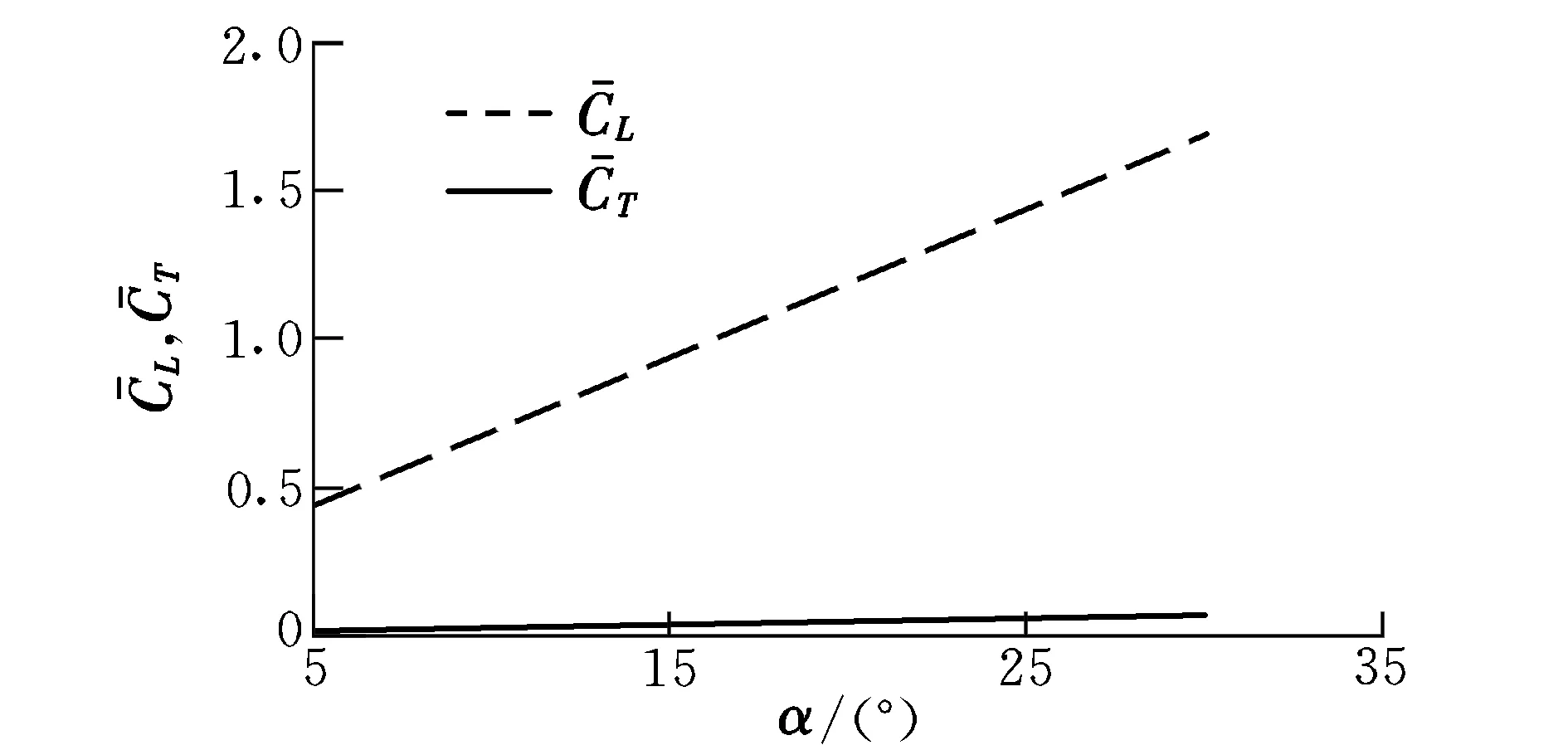
图6　平均输出力系数随迎角的变化Fig.6　Change of average output force coefficient with AOA

4对比研究

为了更进一步对该算法进行研究,采用CFD方法对翅翼进行网格划分,并采用动网格技术对翅翼进行空气动力学分析,发现其运动规律与3.2节中翅翼的运动规律一致。网格划分图、速度等值线图以及升力随时间的变化曲线如图7～图9所示。

图7　网格划分Fig.7　Diagram of meshing

图8　扑翼飞行器速度等值线图Fig.8　Velocity contour of flapping wing aircraft

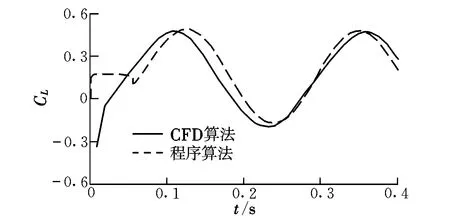
图9　升力系数随时间的变化曲线Fig.9　Curves of CLchange with time

从图9可以看出,两者在总体趋势上吻合得很好,在刚开始扑动时存在一定的差异,这可能是由计算时采用的收敛条件和网格划分的精密度造成的。文献[10]用运动跟踪试验的方法对翅翼进行了空气动力学分析。为了进一步从试验方面与本文算法进行比较,取与文献[10]相同的运动参数及几何参数,计算得到升力随时间的变化曲线如图10所示。

从图10可以看出,该算法与试验结果总体趋势相近,从试验层面验证了该算法在求解扑翼飞行器气动力方面的有效性;另外在平均数值上程序算法比试验结果略大一些,这可能是由于在实际扑动过程中翼面发生了变形,对气动力产生了一定的影响。

5结束语

本文通过对机翼进行非定常空气动力学分析,建立了二维非定常模型,并采用MATLAB编制计算升力系数和推力系数的程序。分别从理论和试验方面验证了该算法的合理性及结果的可靠性。该算法只需输入运动的类型以及运动参数,便可以输出升力系数和推力系数,计算简便高效,便于计算比较不同运动参数对升力系数和推力系数的影响,为扑翼飞行器的优化设计提供了参考。

参考文献：

[1]Weis-Fogh T.Quick estimates of flight fitness in hovering animals,including novel mechanisms for lift production[J].Journal of Experimental Biology,1973,59(1):169-230.

[2]Sun Mao,Du Gang.Lift and power requirements of hovering insect flight[J].Acta Mechanica Sinica,2003,19(5):458-469.

[3]Lin San-Yih,Hu Jeu-Jiun.Numerical study of flapping wing[R].AIAA-2003-3448,2003.

[4]Giesing J P.Nonlinear two-dimension unsteady potential flow with lift[J].Journal of Aircraft,1968,5(2):135-143.

[5]Osbome M F.Aerodynamics of flapping flight with application to insects[J].Journal of Experimental Biology,1951,28(2):221-245.

[6]Bisplinghoff R L,Ashley H,Halfman R L.Aroelasticity[M].Springer New York:Addison-Wesley Publishing Co.,2012:47-53.

[7]Anderson J D Jr.Fundamentals of aerodynamics [M].4th ed.New York:McGraw-Hill Book Company,2005:28-32.

[8]McCune J E,Lam C M G,Scott M T.Nonlinear aerodynamics of two-dimensional airfoils in severe maneuver[J].AIAA Journal,1990,28(3):385-393.

[9]雷亚超.仿蝴蝶微型扑翼机飞行原理及扑翼机构研究[D].南昌:南昌航空大学,2013.

[10]Harmon R L.Aerodynamic modeling of a flapping membrane wing using motion tracking experiments[D].Maryland:University of Maryland,College Park,2008.

(编辑：李怡)

Study on unsteady aerodynamics characteristics of flapping-wing aircraft

WANG Jian-ling, HE Guang-ping, DI Jie-jian

(School of Mechanical and Materials engineering, NCUT, Beijing 100041, China)

Abstract:In order to study aerodynamic characteristics of flapping wing vehicle under complex unsteady motion, for a kind of flapping wing vehicle developed independently, a two-dimensional unsteady aerodynamic force model was established. Based on the model, MATLAB was used to program the code to calculate lift force coefficient and thrust force coefficient. Then, the influence of the parameters on the lift and thrust was calculated and analyzed. The results show that the phase difference has a larger influence on the coefficient of thrust; however, the coefficient of lift changes faster with change of AOA.

Key words:bionics flapping-wing aircraft; non-steady aerodynamics; lift coefficient; trust coefficient

收稿日期:2015-08-19;

修订日期:2016-01-19; 网络出版时间:2016-02-29 16:38

基金项目:国家自然科学基金资助(51375016)

作者简介:王建领(1986-)，男，河南商丘人，硕士研究生，研究方向为仿生扑翼飞行器。

中图分类号：V211.5; V276

文献标识码：A

文章编号：1002-0853(2016)03-0072-04