基于滤波扩张观测器的有限时间收敛制导律

冯丹, 任宏滨, 简金蕾, 吉阳

(空军工程大学 防空反导学院, 陕西 西安 710051)

基于滤波扩张观测器的有限时间收敛制导律

冯丹, 任宏滨, 简金蕾, 吉阳

(空军工程大学 防空反导学院, 陕西 西安 710051)

摘要:为提高拦截机动目标的精度,基于滤波扩张状态观测器提出了一种考虑自动驾驶动态特性的有限时间收敛制导律。通过滤波扩张状态观测器对制导律中目标机动信息进行补偿,使导弹在拦截目标时具有更高的拦截精度。仿真结果表明,在目标机动情况下,设计的制导律能保证视线角速度在有限时间内收敛到零,拦截弹过载较小,具有较好的动态特性和鲁棒性。同时与普通的扩张观测器的估计结果相比,滤波扩张状态观测器对机动目标的跟踪效果较佳。

关键词:终端滑模; 有限时间收敛; 扩张观测器; 机动目标

0引言

导弹要实现精确制导和对目标的准确打击,关键是设计导引律。20世纪90年代提出了终端滑模控制方法。文献[1-2]在设计滑模面时引入了非线性项,保证状态变量在有限时间到达滑模面的同时收敛到平衡点。文献[3-4]解决了近年来引起广泛关注的传统滑模变结构控制方法只能保证系统状态在有限时间达到滑动模态的问题。为解决终端滑模控制方法产生的奇异值问题,文献[5-6]均采用非奇异终端滑模面设计了具有攻击角度约束的制导律,但由于设计中存在目标机动加速度和视线角及其高阶导数等不可测的参量,会影响制导律的精度,文献[7]直接将这些参量忽略,仿真条件过于理想,不适用于实际的拦截情形。

本文基于扩张观测器思想,加入滤波器,构造滤波扩张观测器,提出了一种基于滤波扩张观测器的有限时间收敛制导律,补偿了传统滑模制导律的不确定项部分,从而提高了机动目标的拦截性能。

1弹目相对运动模型

拦截问题的三维模型较为复杂,为研究方便,采用二维制导模型并仅分析纵向平面拦截情况,将导弹和目标均视为质点,质心分别为M,T。弹目相对运动关系如图1所示。图中：Vm,Vt为导弹和目标的速度;am,at为导弹和目标的加速度;θm,θt为导弹和目标的弹道倾角;R为弹目相对距离;q为弹目视线角。

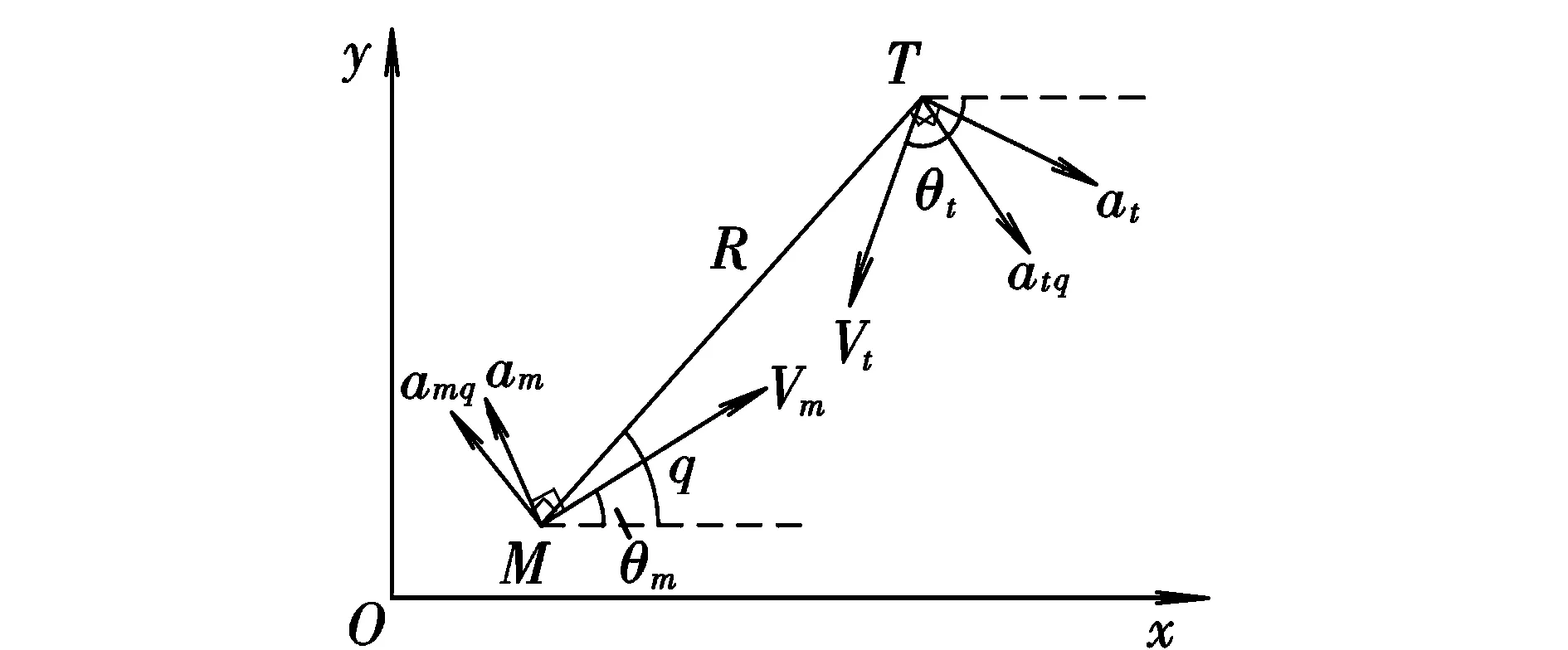
图1　弹目相对运动关系Fig.1　Missile-target relative geometry relation

将速度矢量沿视线方向和垂直视线方向分别进行分解可得弹目相对运动模型:

(1)

(2)

对式(2)两边求导,整理可得:

(3)

式中:atq,amq分别为目标、导弹的加速度沿垂直于视线方向的分量,表达式为:

本文采用雷达导引头,末制导过程满足以下假设[8]:

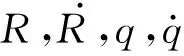
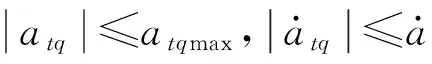
2滤波扩张状态观测器

扩张状态观测器[9](Extended State Observer,ESO)是根据系统外部变量的实测值得到状态变量估计值的一种新型的非线性状态观测器,在观测器基础上将未知函数扩张为新的状态变量,进而得到变量估计值,非常适合机动目标加速度估计问题[10]。但系统量测噪声的存在对观测值的精度影响很大,通常要先对观测器输入滤波,但会造成延时,为此直接将滤波器引入扩张观测器,构成复合系统,推导复合系统的扩张状态观测器,即为滤波扩张状态观测器(FESO)。

(4)

(5)

(6)

则构造复合系统式(6)的扩张状态观测器,得到系统式(3)的滤波扩张状态观测器方程:

(7)

式中:E0为扩张观测器的估计误差;Z0为除噪后的视线角速度;Z1为视线角速度;Z2为观测器输出的目标加速度信息;β00,β01,β02为观测器的增益。

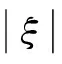
(8)

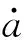
(9)

其中,函数fal定义为:

(10)

式中:0<α<1。若取α1=1/2,α2=1/4[6],将式(10)带入式(9),则系统误差方程为:

(11)

由于系统处于稳定状态时,式(11)中的方程都收敛到零,即:

(12)

由式(12)可以解出系统误差方程的稳态误差为:

(13)

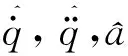
3基于FESO的有限时间收敛制导律

由于末制导律时间非常短,视线角速度如果能在有限时间收敛于零,导弹命中目标的可能性就会大大提高。这里选取滑模面[6,12]:

(14)

式中:β>0,1<γ<2,为设计常数。

为保证系统状态能到达变结构且到达的过程中有优良的动态特性,使用自适应变结构趋近律即:

(15)

(16)

由式(15)和式(16)可得系统的有限时间收敛制导律为:

(17)

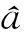
(18)

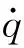
证明:选取Lyapunov函数:

(19)

对式(19)求导,并将导引律式(18)和式(16)带入,得:

(20)

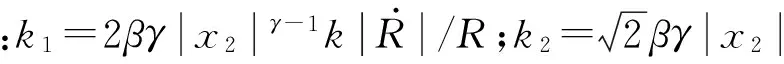
为增加工程实用性,需考虑自动驾驶仪的动态特性;但因其结构复杂,这里将其考虑为一阶环节:

(21)

式中:τ为自动驾驶仪的时间常数;am为自动驾驶仪输出的拦截加速度;amc为提供给自动驾驶仪的制导指令。

(22)

(23)

将式(18)求导后带入式(23)并整理引起奇异的部分,可得:

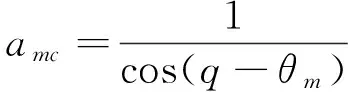
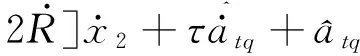
(24)

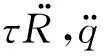
(25)

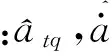
4仿真结果及分析

为验证文中基于FESO的FENTSM性能,将其与传统滑模制导律(SMG)和比例导引律(PN)进行对比。仿真条件为:导弹初始位置为xm=0 m,ym=0 m,速度大小Vm=3 000 m/s,初始弹道倾角θm=0°,导引盲区为300 m;目标速度大小为Vt=1 000 m/s,初始弹道倾角θt=10°,初始位置xt=21 213 m,yt=21 213 m,目标的机动加速度为at=5g×sin(πt) m/s2,其中k=3,τ=0.3,g=9.8 m/s2,β=0.35,γ=1.6。

非线性函数fal中参数α与观测器阶数有关,β0i与积分步长h相关,工程经验[11]可大概确定滤波扩张状态观测器参数为β00≈1/h,β01≈0.3/h2,β02≈0.0001/h3。根据经验值并结合本文实际,通过仿真选取FESO的参数为:β00=50,β01=790,β02=1320,α1=0.85,α2=0.15,δ1=0.2,δ2=0.1。仿真结果如图2～图5所示。

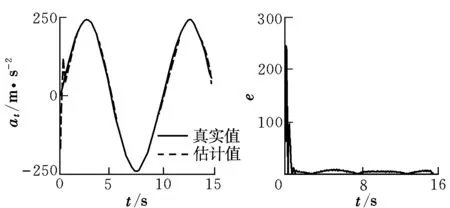
图2　FESO的目标加速度估计结果及观测误差Fig.2　The FESO estimation value of target’s 　　　acceleration and estimation error value

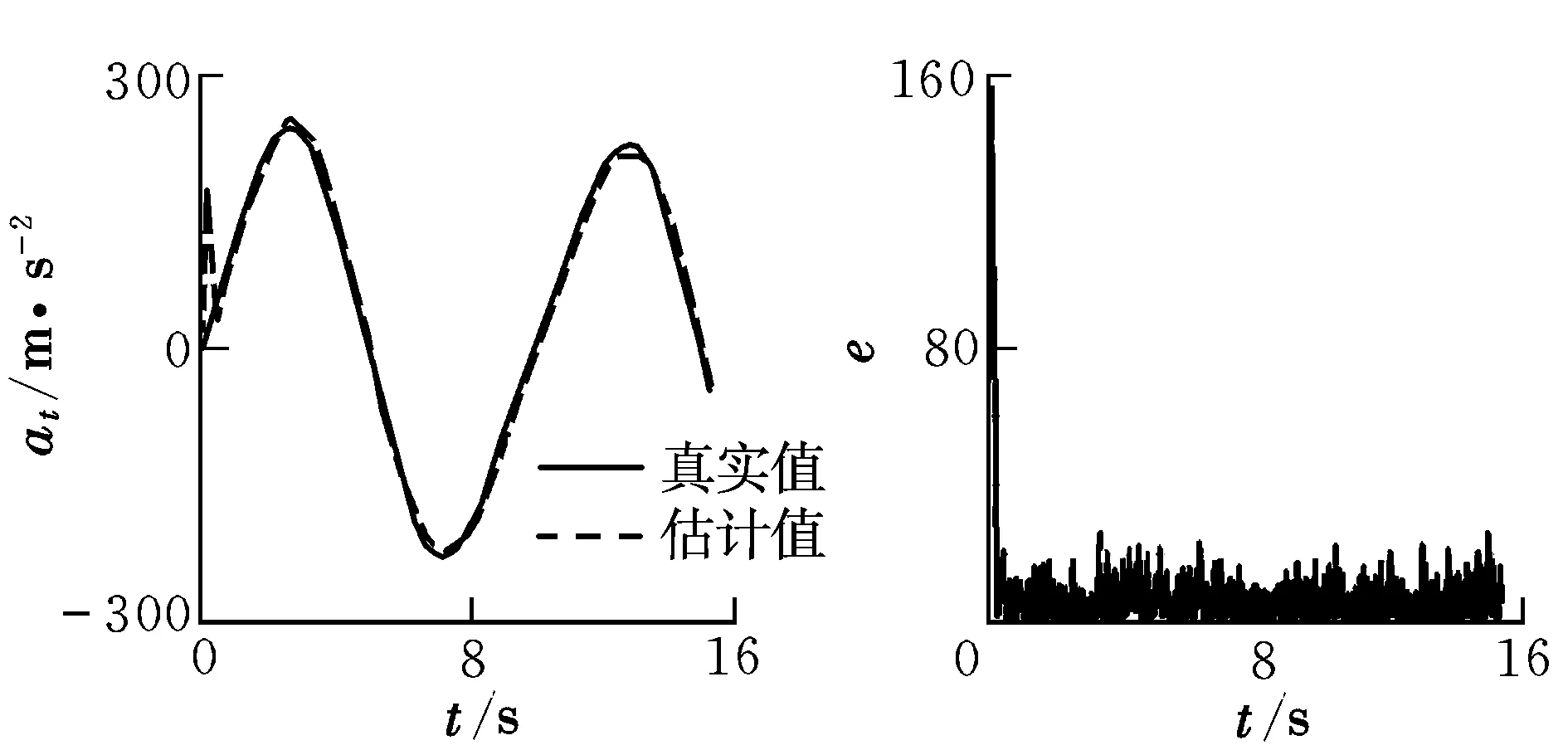
图3　ESO的目标加速度估计结果及观测误差Fig.3　The ESO estimation value of target’s acceleration and estimation error value

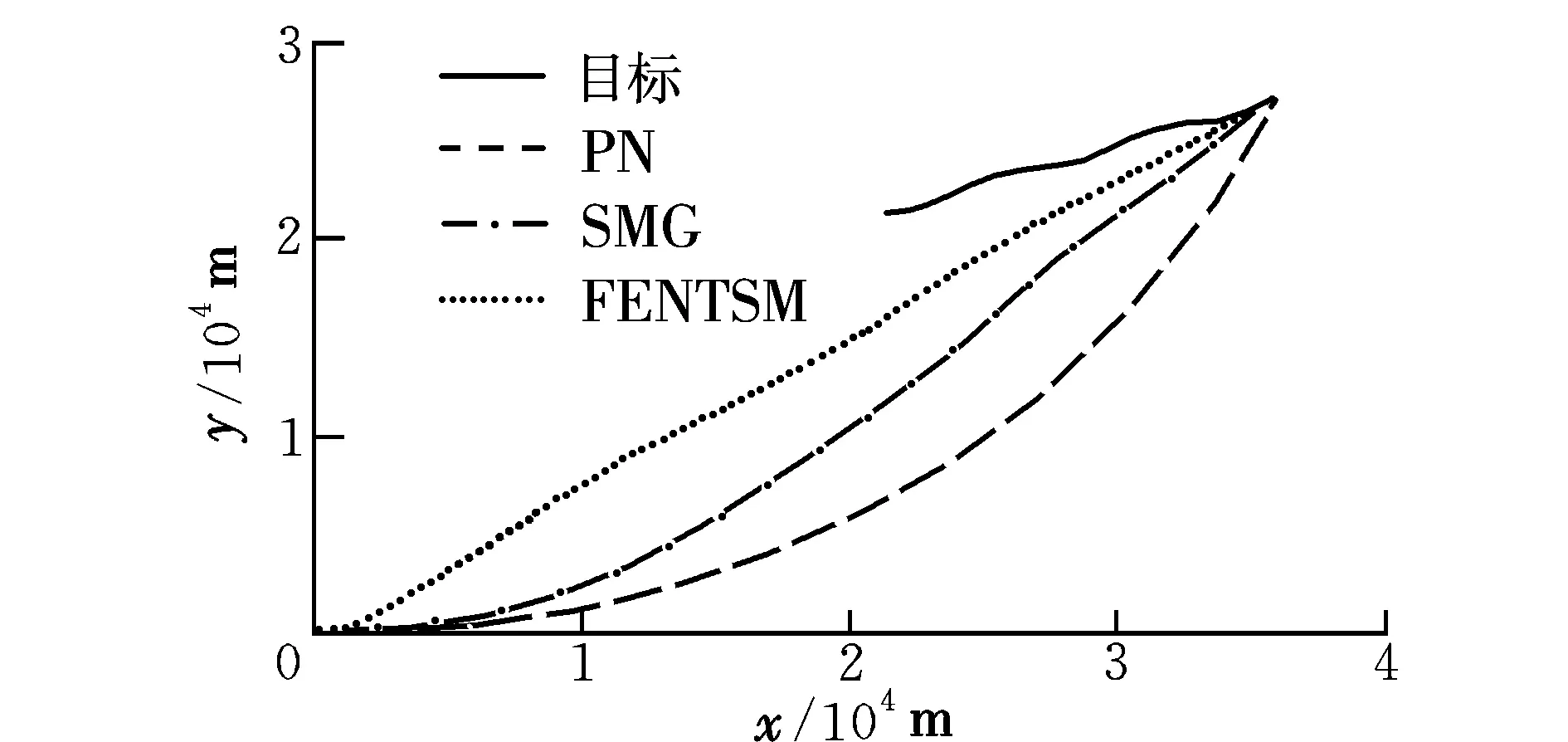
图4　弹目飞行轨迹Fig.4　Missile-target flight trajectories

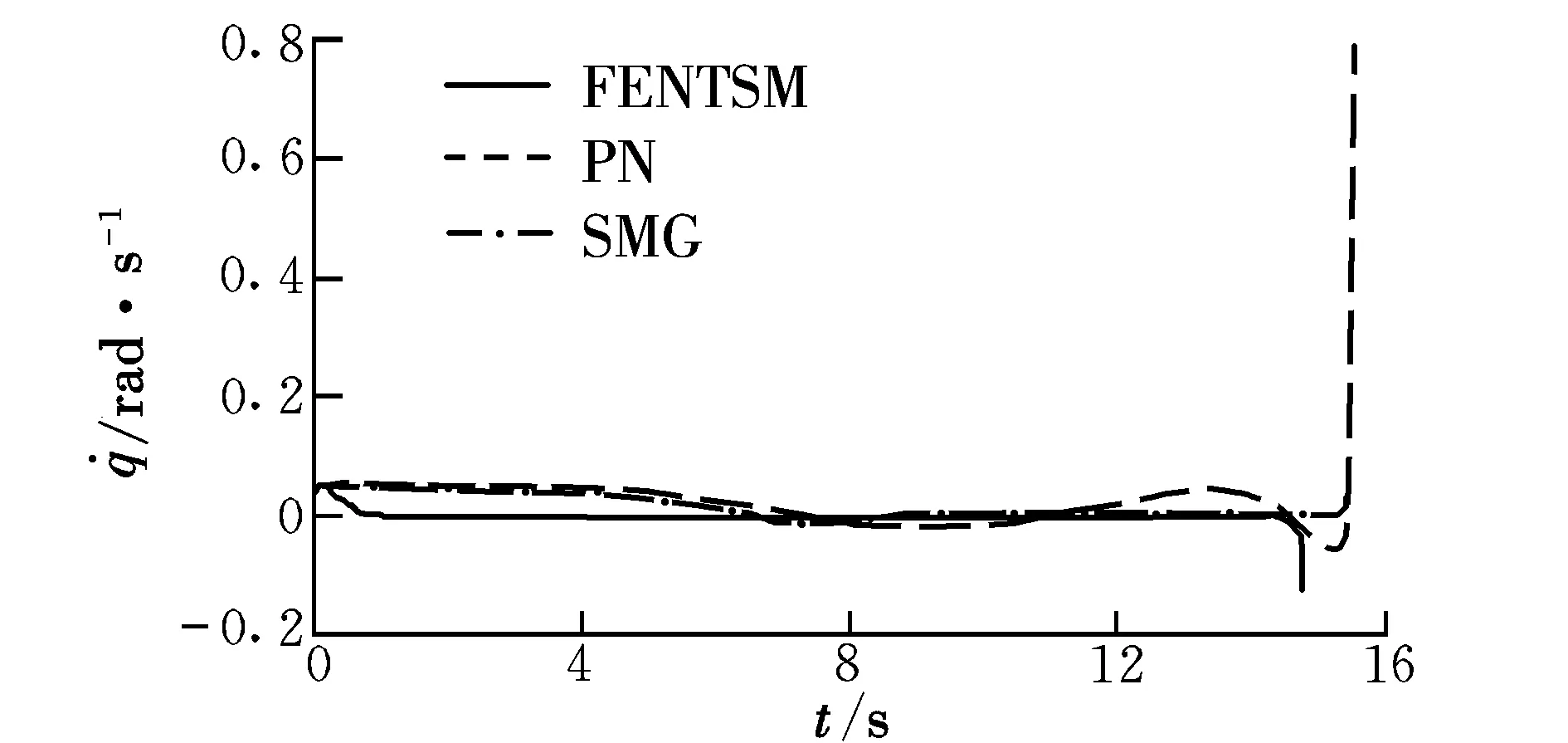
图5　正弦机动下视线角速度的对比Fig.5　The contrast of line-of-sight rate with sine

图2和图3分别为FESO和普通ESO对目标机动加速度的估计结果和观测误差。明显可以看出,FESO跟踪目标机动加速度效果好,基本可以实现实时跟踪，而且观测误差很小,收敛速度也较快。图4为目标做正弦机动时SMG,PN和FENTSM的运动轨迹,可以看出三种制导律都能成功击中目标,但FENTSM的过载小,制导性能明显优于SMG和PN。图5为目标做正弦机动时的视线角速度变化,可以看出三种方法都可收敛到零,但FENTSM收敛速度最快,在1 s左右,保证了视线角速度在有限时间内收敛到零。PN收敛时间较长，并且视线角速度曲线有振荡。

表1为三种制导律在拦截正弦机动目标时的不同制导效果,其中FENSM拦截时间最短,脱靶量更小。对比仿真结果可知,FENTSM对拦截机动目标的性能明显提高。

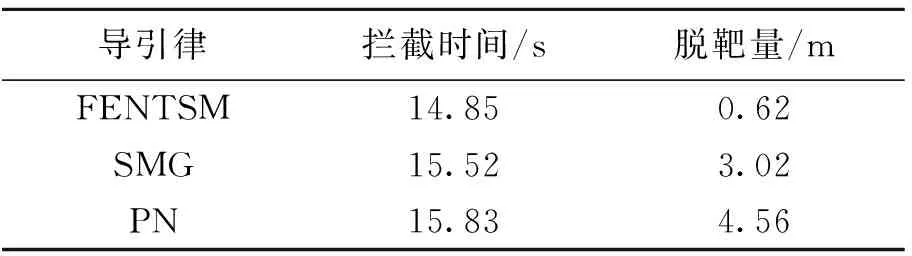
表1　拦截正弦机动目标的效果对比

5结论

本文考虑自动驾驶仪动态特性,通过滤波扩张观测器补偿未知干扰项,设计了一种基于滤波扩张观测器的有限时间收敛制导律,通过理论分析和仿真验证得出以下结论:

(1)设计的滤波扩张状态观测器能够同步跟踪机动目标,反馈目标的加速度信息,相较于普通的扩张状态观测器,还具有滤除量测噪声的功能,并且收敛速度快,跟踪效果好。

(2)本文设计的基于滤波扩张状态观测器的有限时间收敛制导律,使视线角速度有限时间收敛到零,提高了拦截精度。同时考虑了自动驾驶仪动态特性,使设计的制导律鲁棒性更强,更加符合实际。

参考文献：

[1]Man Z,Paplinski A P,Wu H R.A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators[J].IEEE Transactions on Automatic Control,1994,39(12):2464-2469.

[2]Feng Yong,Yu Xinghuo,Man Zhihong.Non-singular terminal sliding mode control of rigid manipulators [J].Automatica,2002,38(12):2159-2167.

[3]Zhou D,Mu C D,Xu W L.Adaptive siding-mode guidance of a homing missile [J].Journal of Guidance,Control,and Dynamics,1999,22(4):589-594.

[4]XU Zhaoxin,HUA Wenhua,CHEN Xinglin.Sliding-mode guidance law based on adaptive observation techniques[C]//The 2nd International Conference on Intelligent Control and Information Processing.Harbin:IEEE,2011:743-747.

[5]熊少锋,王卫红,王森.带攻击角度约束的非奇异快速终端滑模制导律[J].控制理论与应用,2014,31(3):269-278.

[6]周慧波,宋申民,刘海坤.具有攻击角约束的非奇异终端滑模导引律设计[J].中国惯性技术学报,2014,22(5):606-611,618.

[7]Zhou D,Mu C D,Ling Q.Optimal sliding-mode guidance of a homing missile[J].Chinese Journal of Aeronautics,1999,12(4):236-241.

[8]Shtessel Y,Shkolnikov L,Levant A.Guidance and control of missile interceptor using second-order sliding modes[J].IEEE Transaction on Aerospace and Electronic Systems,2009,45(1):110-124.

[9]张尧,郭杰,唐胜景,等.基于扩张状态观测器的导弹滑模制导律[J].北京航空航天大学学报,2015,41(2),343-350.

[10]姚郁,王宇航.基于扩张状态观测器的机动目标加速度估计[J].系统工程与电子技术,2009,31(11):2682-2684,2692.

[11]韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M]北京:国防工业出版社,2008:221-237.

[12]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:44-45.

(编辑：方春玲)

Finite time convergent guidance law based on filtering extended state observer

FENG Dan, REN Hong-bin, JIAN Jin-lei, JI Yang

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

Abstract:Based on the technology of extended state observer with filter(FESO), a finite time convergent guidance law (FENTSM) was derived to improve precision of intercept maneuvering target. This method could estimate target maneuvering acceleration according FESO and dynamically compensate guidance law which improved operating precision when intercepting maneuvering target. The simulation results indicate that this guidance law makes rate of LOS angle convergence in a finite time and has lower load on the interception missile, which has good dynamic performance and robustness. Meanwhile the simulation results verify that the FESO has better tracking effect compared with the usually ESO to maneuvering target.

Key words:terminal sliding mode; finite time convergent; extended state observer; maneuvering target

收稿日期:2015-07-14;

修订日期:2015-12-10; 网络出版时间:2016-01-10 14:10

作者简介:冯丹(1991-)，女，陕西兴平人，硕士研究生，研究方向为导航、制导与控制。

中图分类号：V448.13

文献标识码：A

文章编号：1002-0853(2016)03-0062-05