序列低频重乘积关系计算算法的研究*

胡建勇，张文政，董新锋

(保密通信重点实验室，四川 成都 610041)



序列低频重乘积关系计算算法的研究*

胡建勇，张文政，董新锋

(保密通信重点实验室，四川 成都 610041)

摘要：针对周期序列实现有效的离散傅里叶频谱攻击，前提条件是寻找到序列的一对低频重乘积关系。基于低频重乘积关系如何计算的问题，在时域上提出了通常的低频重乘积关系计算算法。为了减少计算算法的遍历复杂性，利用序列的频域特性和迹表示，在频域上提出了更加有效的低频重乘积关系计算算法。最后，针对频域上的低频重乘积关系计算算法，分别利用迹函数的乘积关系以及满足乘积关系序列在频域上的等价条件，给出了关于乘积序列迹表示的两种适用计算方法。

关键词：频谱攻击；低频重；乘积关系；频域特性；迹表示

0引言

离散傅里叶频谱攻击[1-3]是针对周期序列的一类代数攻击[4-9]，其在频域上建立起以参照序列与输出序列时间间隔为未知量的方程并求解，最后恢复出密钥或者计算出输出序列的后续比特。离散傅里叶频谱攻击的有效实现严重依赖于序列低频重乘积关系[1,2,10]的计算。当已知的输出序列比特数小于该序列的线性复杂度时，对周期序列进行离散傅里叶频谱攻击的先决条件，是寻找到该周期序列的一组低频重乘积关系，并且这对低频重乘积关系的线性复杂度严重影响离散傅里叶频谱攻击的数据复杂度。事实上，在给定序列a的一组低频重乘积关系b和u时，离散傅里叶频谱攻击的数据复杂度为l(b)+l(u)。因此，一组低频重乘积关系的线性复杂度之和越小，离散傅里叶频谱攻击的数据复杂度就越小。

既然低频重乘积关系对于离散傅里叶频谱攻击具有如此重要的作用，那么就有必要对低频重乘积关系作进一步研究，比如研究低频重乘积关系的计算。但是目前为止，尚未有文献给出具体的低频重乘积关系的计算算法。

本文的目的就是研究如何快速计算序列的低频重乘积关系，分别从时域上和频域上提出低频重乘积关系的计算算法，从而完善离散傅里叶频谱攻击的相关理论研究，弥补就低频重乘积关系如何计算这一问题的短缺。

1预备知识

为了便于理解，这里先将本文用到的记号以及数学知识作简要说明。

n：正整数，通常取为线性反馈移位寄存器的位数；

N：等于2n-1，之所以取这样的N，是因为基于n位线性反馈移位寄存器产生的序列，不论是滤波序列，还是组合序列，N一定是其一个周期，即其最小周期一定能被N整除；

a：周期为N的二进制序列；

l(a)：序列a的线性复杂度；

α：域F2n上阶为N的元素，通常选本原元；

ns：使得等式s≡s2t(mod N)成立的最小t值；

Cs：代表元为s的分圆陪集，定义为Cs={s2imod N|i=0,1,…,ns-1}，Cs中的最小元素称为分圆陪集首。不失一般性，就定义s为Cs的分圆陪集首。

Γ2(N)：在模N的意义下，所有分圆陪集首构成的集合。

周期序列a的离散傅里叶频谱变换定义为：

离散傅里叶频谱逆变换定义为：

序列A称为a的离散傅里叶频谱序列，简称频谱序列。频谱序列中非零频谱值的个数，定义为序列的频谱重量。事实上，一个序列的频谱重量就等于该序列的线性复杂度。令：

则有

at=A(αt)更进一步A(x)可以写成序列迹表示[10]的形式：

从而得到序列a的迹表示：

记Na为序列a对应频谱序列A中非零频谱值构成的集合，具体定义为：

Na={k∈Γ2(N)|Ak≠0}

于是，序列的迹表示可以简化为：

给定序列a，当序列b和u满足下列两个关系时：(1)乘积关系u=a∘b；(2)线性复杂度关系l(u)+l(b)≤l(a)时，就称(b，u)是序列a的一组低频重乘积关系。

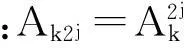
引理2[12]：若时序上周期为T的序列a,c,d，满足：d=a∘c，其充要条件是在频域上满足：

其中m=0,1,…,T。

2时域上低频重乘积关系的计算

取定一个序列b，u便可以根据u=a∘b计算得出，因此最直接的方法是遍历所有的b，再验证b和u是否满足线性复杂度关系。然而考虑到遍历复杂度的问题，通常先利用线性复杂度关系过滤掉一些序列b。当序列b和u满足线性复杂度关系，即l(u)+l(b)≤l(a)时，则序列b必须满足：

0l(b)≤l(a)

(1)

由于通常的低频重乘积关系计算算法未涉及序列的傅里叶频谱值，不妨称通常的低频重乘积关系计算算法为时域上的低频重乘积关系计算算法，具体细节如算法1所述：

算法1：时域上的低频重乘积关系计算算法。

已知条件：给定N比特序列a。

目的：求解序列b和u，使得u=a∘b，且满足l(u)+l(b)≤l(a)。

算法过程：

(1)初始化：t=0，b=0，V为所有N比特序列构成的集合。

(2)V=V/b，任意选取b∈V,t=t+1。如果t≻2N-1，输出“不存在这样的低频重乘积关系”，程序结束；否则，执行步骤(3)。

(4)计算u=a∘b，得到u的线性复杂度l(u)。如果l(u)+l(b)≤l(a)，则输出b和u；否则，转回步骤(2)。

时域上的低频重乘积关系计算算法虽然利用了序列b的线性复杂度性质过滤掉一些序列b，在一定程度上降低了算法的复杂度。但是由于序列b无论如何仍要遍历整个集合V，并且对于每个序列b，都要计算其复杂度。相对地，序列u则是通过序列b的过滤而直接避免被计算，从这个层面上来说，真正过滤的是序列u。并且b确定时，序列u也跟着确定。因此如何利用序列b的线性复杂度性质，使得不满足要求的序列b直接不被选取，减少序列b的遍历复杂度，真正意义上过滤掉一部分序列b，是进一步优化算法，减少算法复杂度的关键。

3频域上低频重乘积关系的计算

利用序列的迹表示，可以很快计算该序列的线性复杂度。假设序列a的迹表示式为：

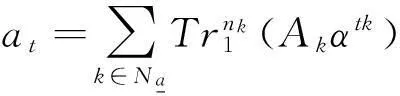
其中,t=0,1,…,N-1，那么序列a的线性复杂度可由公式：

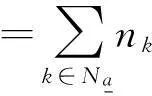
(2)

快速计算得出。由此可以看出，一个序列的线性复杂度只与对应频谱序列的非零项的个数有关，并且频谱序列中非零项对应的分圆陪集首一旦确定，频谱序列的非零项个数就确定了，换句话说，该序列的线性复杂度就确定了。因此，确定序列a的线性复杂度，关键在于集合Na的确定，根本无需知道序列a的任何比特。

对于任意N比特长度序列a，集合Na⊆Γ2(N)。欲求序列a的一组低频重乘积关系(b，u)，首先计算序列a的离散傅里叶频谱序列，得到其迹表示，然后猜测序列b的迹表示。虽然不知道具体的Nb，但同样有Nb⊆Γ2(N)。由关系式(1)和线性复杂度的计算式(2)知：

0(a)

(3)

因此只需在集合Γ2(N)中选择恰当的分圆陪集首k满足关系式(3)，便可在选取序列b之前，直接过滤掉一部分序列。定义集合

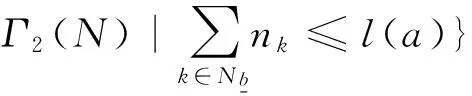
选定好分圆陪集首后，假设：

Nb={r1,r2,…,rt}

其中t为集合Nb的大小，对于每一个k∈Nb，Bk的可选值有2nk-1个，定义集合

M2={(Br1,Br2,…,Brt)|Bri∈F2nk/0}

其中ri∈Nb,i=1,2,…,t，从而具有相同线性复杂度的序列b的总个数为：

然后根据乘积关系u=a°b，得到u的迹表示，计算u的线性复杂度。最后验证b和u是否满足线性复杂度关系。于是得到新的低频重乘积关系计算算法，由于新的低频重乘积关系计算算法用到了序列的离散傅里叶频谱值，称这样的算法为频域上的低频重乘积关系计算算法，具体细节如算法2所述：

算法2：频域上的低频重乘积关系计算算法

已知条件：给定N比特序列a；

目的：求解序列b和u，使得u=a∘b，且满足l(u)+l(b)≤l(a)。

算法过程：

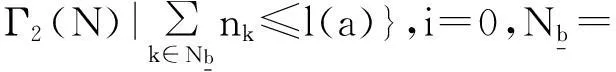
步骤2：M1=M1/Nb，任意选取Nb∈M1，i=i+1。如果i≻|M1|，输出“不存在这样的低频重乘积关系”；否则，执行步骤3。

步骤3：M2={(Br1,Br2,…,Brt)|Bri∈F2nk/0}，j=0，(Br1,Br2,…,Brt)=(0,0,…,0)。

步骤4：M2=M2/{(Br1,Br2,…,Brt)}，任意选取(Br1,Br2,…,Brt)∈M2，j=j+1。如果j≻|M2|，返回步骤2；否则执行步骤5。

步骤5：计算u=a∘b，得到u的线性复杂度l(u)。如果l(u)+l(b)≤l(a)，则输出b和u；否则，转回步骤4。

算法2——频域上的低频重乘积关系计算算法中，步骤4选择序列b的非零离散傅里叶频谱值，相当于选择具体的序列b，而在此之前，利用序列b应该满足的线性复杂度关系，使得满足条件的Nb构成集合M1，遍历时直接在集合M1中选取适当的Nb，从而达到选取序列b之前，预先过滤掉一部分序列的效果。

与算法1相比，算法2利用低频重乘积关系的线性复杂度关系，在遍历序列b之前，率先过滤掉一部分不满足条件的序列，减少了遍历的复杂度，这是算法1不能达到的，因此算法2的算法复杂性要小于算法1的算法复杂性。另外，算法2充分利用序列的频域性质，实现在频域上计算低频重乘积关系，这也为低频重乘积关系的计算提供一种新的方式。

值得一提的是，算法2中步骤5计算序列u，与算法1中的计算也有区别。算法1中由于知道序列b的每一位，直接对应位相乘，便可得到序列u的每一位。而算法2直接将序列a的迹表示与序列b的迹表示相乘，得到序列u的迹表示，从而快速计算u的线性复杂度，避免了序列u的比特位计算，减少了算法的计算复杂性。

利用序列的迹表示相乘是计算序列u的迹表示的方法之一，这里还有另外一种方法。序列u的迹表示的形式如下：

因此只需确定Uk的值即可。根据引理2，可以得到:

(4)

注意这里并不需要对所有的k，计算出Uk，而仅仅对于k∈Γ2(N)，计算Uk即可。计算式(4)中，频谱序列A可由序列a通过离散傅里叶变换得到，频谱序列B则满足：当k∈Nb时，步骤(4)已经取定了Bk；当k∈Γ2(N)/Nb时，Bk=0；而对于k∉Γ2(N)，均可根据引理1计算得出。因此计算Uk是可行的，最后求解出序列u的迹表示。与直接利用序列的迹表示相乘相比，迹表示相乘的计算方法主要的计算复杂性在于迹函数的相乘，而这种计算方法需要计算序列b的所有频谱值，尽管可根据引理1快速计算得出，但还是无法避免增加整个算法的计算复杂度和数据复杂度。

4结语

鉴于低频重乘积关系对于离散傅里叶频谱攻击的重要性，本文对序列的低频重乘积关系计算算法进行了研究，分别提出了时域上的低频重乘积关系计算算法和频域上的低频重乘积关系的计算算法，对有效实现序列的离散傅里叶频谱攻击具有重要的作用。

另外，引入指示器随机变量Ik，Ik的具体定义为：

则序列b的线性复杂度可通过以下方式计算：

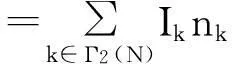
假如我们能够根据乘积关系u=a°b得到序列u的线性复杂度和指示器随机变量Ik的关系，那么就可以将低频重乘积关系的计算问题转化为0-1整数规划问题。因此，下一步的计划主要是研究如何将序列u的线性复杂度的变量转化为关于指示器随机变量Ik的函数。

参考文献：

[1]GONG G,Rønjom S,Helleseth T.Fast Discrete Fourier Spectra Attacks on Stream Ciphers[J].IEEE Transactions on Information Theory.2011,57: 5555-5565.

[2]王晶晶,陈克非.序列快速傅里叶攻击的改进 [J].上海交通大学学报:自然版，2012,46(02): 285-288.

WANG Jing-jing,CHEN Ke-fei.Improvement of Discrete Fourier Transform Attack[J].Journal of Shanghai Jiaotong University.2012,46(02): 285-288.

[3]王晶晶.序列密码的快速离散傅里叶频谱攻击[D].上海交通大学硕士论文，2013: 13-34.

WANG Jing-jing.Fast Discrete Fourier Spectra Attacks of Stream Ciphers[D].Shanghai Jiaotong University.2013: 13-34.

[4]Courtois N.Fast Algebraic Attacks on Stream Ciphers with Linear Feedback[C].Advances in Cryptology-CRYPTO 2003.Springer-Verlag.2003,2729:176-194.

[5]董军武.DES的S盒的布尔性质[J].通信技术，2012,45(12): 66-70.DONG Jun-wu.Boolean Properties of DES′s S-Boxes[J].Communications Technology.2012,45(12):66-70.

[6]Armknecht F.Improving Fast Algebraic Attacks[C].FSE 2004.Springer-Verlag.2004,3017: 65-82.

[7]Courtois N,Meier W.Algebraic Attacks on Stream Ciphers with Linear Feedback[C].Advances in Cryptology - Eurocrypt’2003.Springer-Verlag.2003,2656:345-359.

[8]Armknecht F,Krause M.Algebraic Attacks on Combiners with Memory[C].Advances in Cryptology - CRYPTO 2003.Springer-Verlag.2003,2729:162-176.

[9]Helleseth T,Rønjom S.Simplifying Algebraic Attacks with Univariate Analysis[C].Information Theory and Applications Workshop (ITA),2011.[S.l.]: IEEE,2011: 1-7.

[10]WANG Jing-jing,CHEN Ke-fei,ZHU Shi-xiong.Annihilators of Fast Discrete Fourier Spectra Attacks[C].Advances in Information and Computer Security.Heidelberg: Springer,2012:182-196.

[11]Rønjom S,Gong G,Helleseth T.On Attacks on Filtering Generators Using Linear Subspace Structures[C].Sequences,Subsequences,and Consequences.Berlin Heidelberg: Springer,2007,4893: 204-217.

[12]胡建勇，张文政.一类低频重零化子的推导及频谱分析[J].计算机应用，2015,35(12):3447-3449,3445.

HU Jian-yong,ZHANG Wen-zheng.Derivation and Spectrum Analysis of A Kind of Low Weight[J].Journal of Computer Applications.2015,35(12):3447-3449,3455.

Computational Algorithms of Product Relations with Low Spectral Weight

HU Jian-yong,ZHANG Wen-zheng,DONG Xin-feng

(Science and Technology on Communication Security Laboratory,Chengdu Sichuan 610041,China)

Abstract：For implementing effective discrete fourier spectral attack on periodic sequence,the premise condition is to find a pair of product relations with low spectral weight.Based on the problem of how to calculate the product relations,a general computational algorithm for product relations with low spectral weight is proposed in time domain.In order to reduce the traversing complexity in calculating product relations with low spectral weight,by using the spectral properties and the trace representations of sequences,a more effective computational algorithm is proposed in frequency domain.Finally,based on computational algorithm for product relations with low spectral weight in frequency domain,and by using the product relation of trace representations and meeting the equivalent condition of product-relation sequence in frequency domain,two applicable methods for calculating trace representation of product sequences are presented.

Key words：spectral attack; low spectral weight; product relations; spectral property; trace representation

doi:10.3969/j.issn.1002-0802.2016.02.018

* 收稿日期：2015-09-11；修回日期：2015-12-19Received date:2015-09-11；Revised date：2015-12-19

基金项目：保密通信重点实验室基金项目(No.9140C110203140C11049)

Foundation Item:Foundation of Science and Technology on Communication Security Laboratory (No.9140C110203140C11049)

中图分类号：TP309

文献标志码：A

文章编号：1002-0802(2016)02-0217-04

作者简介：

胡建勇(1990—)，男，硕士研究生，主要研究方向为密码学；

张文政(1966—)，男，硕士，研究员，主要研究方向为密码学；

董新锋(1985—)，男，硕士，工程师，研究方向为密码学。