一种两级Polar码串行级联算法研究*

2016-07-01吴东升刘爱军张应宪张青双

通信技术 2016年2期

吴东升，刘爱军，张应宪，张青双

(解放军理工大学通信工程学院,江苏南京 210007)

一种两级Polar码串行级联算法研究*

吴东升，刘爱军，张应宪，张青双

(解放军理工大学通信工程学院,江苏南京 210007)

摘要：极化码(Polar)作为目前唯一一种从理论上证明了能够达到香农(Shannon)极限的码字，且编译码复杂度低，已成为编码领域的一大研究热点。然而，受信道极化速度的限制，有限码长的Polar码性能劣于当前应用比较成熟的LDPC码，Turbo码等。基于此，提出了基于两级极化的级联编码方案，并针对该编码方案采用了改进的译码算法，实现了有限码长Polar码的性能提升。仿真结果显示，性能提升约0.3 dB。文章的研究成果将为提升有限码长Polar码性能开辟一条有效途径。

关键词：有限码长；系统极化码；两级极化码；改进的译码算法

0引言

1948年，Shannon在“通信中的数学理论”研究论文中提出[1]，在有噪声的信道条件下，如果信息传输速率小于信道容量，存在一种编码方式使得在码长趋于无穷时，信息传输错误概率趋近于0。在此基础上，Shannon采用随机编码的方法证明了这个著名的有噪信道编码定理[2]。近几十年来，众多学者一直致力于寻找能够达到该极限的码字，直到极化(Polar)码的出现。

Polar码的核心思想是建立在信道极化理论的基础上。信道极化理论最早由Arikan在2005年IEEE国际信息理论研讨会上提出[3]，其基本原理是通过信道的重组与拆分提高信道的截止速率。随后Arikan提出了一种以2为基数的DMC迭代重组与拆分的特殊方法，在理论分析的基础上，提出了利用该迭代重组与拆分过程进行编译码的思想[4]，从而标志着Polar码的正式问世。由于Polar码从理论上证明了可获得香浓(Shannon)极限容量，因此该编码方案一经提出，立刻引起了科研工作者的广泛关注。

在文献[5]，详细的介绍了离散无记忆信道(Discrete Memory-less Channel，DMC)的Polar编码方法，分析了其可获得的最大码率，并基于信道重组与拆分变换过程给出了Polar码的第一种译码算法，即连续删除(SC)算法。在此基础上，分析了基于SC译码算法性能界，证明了在保持关于码长的对数编译码复杂度条件下，当码长趋于无穷时，Polar码可获得Shannon极限性能。

然而，从现有研究成果可以看出，虽然Polar码能够从理论上证明可获得Shannon极限性能，但是相比于现有应用相对成熟的近Shannon极限的编码方案，如Turbo码、低密度校验(Low-Density Parity-Check,LDPC)码，Polar码在有限码长时的误码率性能还比较差。

围绕该点，本文首先概述信道极化基本理论，随后，论文将重点分析影响Polar码误码率性能的主要原因，并提出了通过内码编码以实现性能增益的方案。论文的主要结论将为Polar码的有限码长性能研究提供新的方向。

2信道极化与系统Polar码编码

2.1信道极化

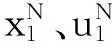
(1)

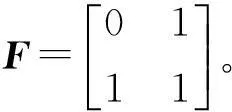
对于二进制擦除信道和二进制对称信道，文献[5]中提出可采用计算各子信道的B-因子(Bhattacharyya因子——信道最大似然检测错误概率的上界)，其定义为：

(2)

式中，对于码长为N的Polar码，经过信道极化后，各个比特信道的转移概率为[4]：

(3)

通过计算上两式可以得到各个子信道的B-因子，从中选取性能较优的作为。然而实时上在实际应用和仿真中往往遇到的是二进制加性高斯白噪声(AWGN)信道，而上述方法很难获得此时各子信道准确的B-因子。本文采用文献[6]所述的高斯近似的方法。对与高斯随机噪声下的各子信道有：

(4)

(5)

(6)

其中:

(7)

文献[7]给出了此时各子信道误码率的计算公式如下：

(8)

由此我们获得了各个子信道误码率的近似值，在此基础上我们对各子信道进行划分，性能优异的部分用来传输用户信息，剩下的部分传输固定的信息。

2.2Polar系统码编码

将式(1)改写如下：

x=uAGA+uACGAC

(9)

式中，矩阵GA和GAC为GN的子集，且分别以A和AC为索引保留了GN中的各列。

在系统Polar码中，编码后的码字由两部分组成，xB和xBC。其中，B为整数集的子集，BC为其补集。由此，式(9)可改写为：

xB=uAGAB+uACGACB

(10)

xBC=uAGABC+uACGACBC

(11)

式中，GAB保留了GA中以B为索引的各列，同理于其他矩阵。由于uAC是一个零向量，因此由信息码字xB获得校验码字的公式如下：

xBC=xB(GAB)-1GABC

(12)

3Polar码内码构造

文献[8]中指出对于码长趋于无穷时的Polar码，其理论性能可到达香农极限。然而，对于有限码长的Polar码，尤其是短码长的时候，由于信道极化速度慢的原因，其性能相比Turbo码LDPC等一直不理想。

如图1所示，经过极化后仍有部分子信道的信道容量介于0和1之间，由于完全好的信道数有限，则在传信息时被迫使用这些不好不坏的信道，而这些差的信道很大程度上决定了Polar码的误码性能。

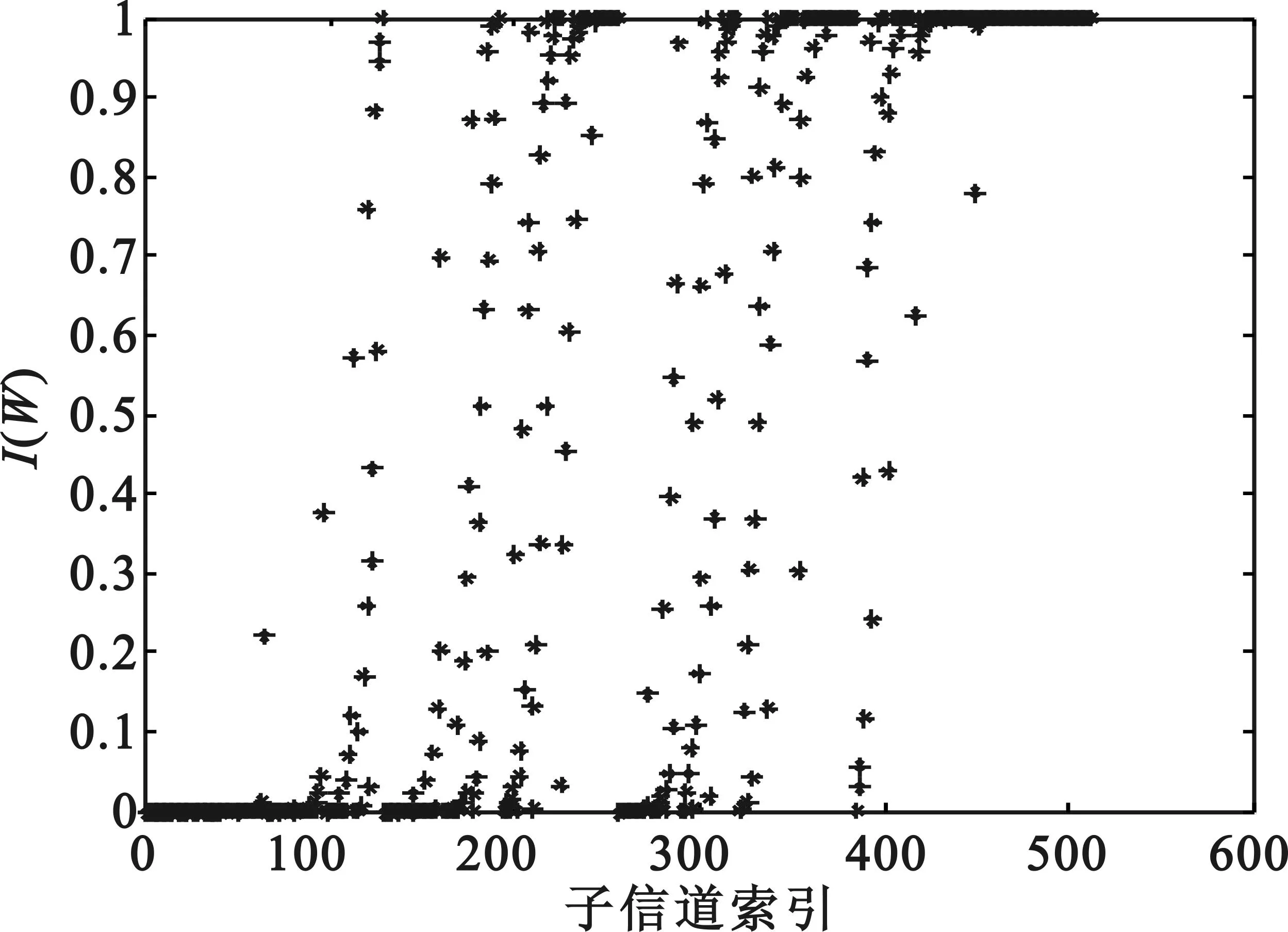
图1　信道极化

文献[9]提出了通过对部分子信道进行汉明码编码的形式保护这些相对较差的信道，从而从总体上实现码字性能的提升。受此启发，本文提出通过系统Polar码对不稳定子信道进行二次极化的方式以提高Polar码的性能。具体做法如下。

3.1内码构造

对于构造一个码长为n，信息位数为k的内码C(n,k)，具体步骤如下：

(1) 首先对Polar码的各比特信道按照可靠度进行排序。对于码长为n的内码J=(j1,j2,…,jn)，若信息位数为k，则从原Polar码信息位中选出k位最不稳定的作为内码的信息位，而后从原Polar冻结位中选出n-k位最稳定的作为内码的校验位。令信息位的集合为I，校验位的集合为H，则I∪U=J。

(2) 对指定信息位上的信息进行系统Polar码的编码，并将生成的校验位赋给H中的各信息位。因此内码的码率R=k/n，本文采用码率为0.5的系统Polar码，则k=n/2。

在完成内码编码后，编码后的内码码字连同其他用户信息一起进行Polar码的编码实现串行级联。如图2所示。

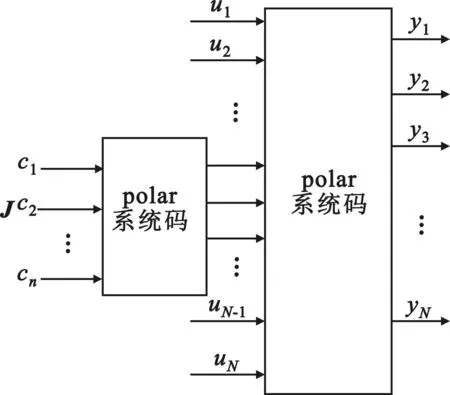
图2　码字构造方案

3.2译码

(13)

本文采用文献[9]中提出的改进后的SC译码算法。开始阶段该译码算法同SC译码算法一样，译码进程从第一位开始按照式(13)规则依次向后译码，而当译码路径行进到J=(j1,j2,…,jn)中各信息位时，译码路径分裂为并行的复数列，如图3所示。

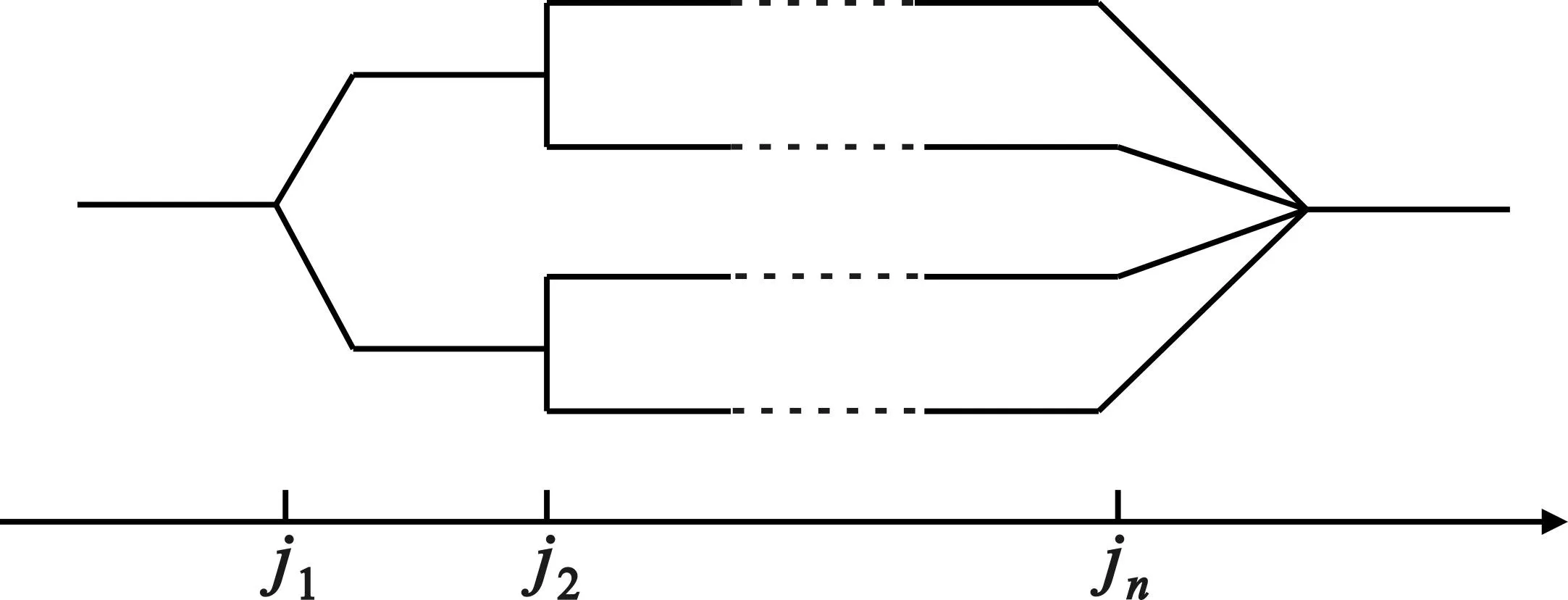
图3　译码进程

当译码路径行进到内码的校验位时，不再依据接收的信息进行估计，而是根据之前的信息位信息直接赋值。最后当译至jn位时，根据比较各路径的似然信息，从2k条路径里选出一条，接下来的译码过程将沿着选出的路径以SC算法向后译码。

4性能分析

仿真过程中采用码长为256，总体码率为0.5的polar码，并在其中构造了三组码长为8的系统Polar码，具体选取的用于构造内码的子信道如下：

经过两级级联编码后的码字相比原码字并没有额外增加冗余，其码长、码率与原码字保持不变。图4给出了仿真的性能曲线，由图可以看出通过采用内码编码和改进后的译码方案，总体性能提升约0.3 dB。图中虚线所示的性能曲线表征所有内码涉及的信息位都完全正确译码的情况下Polar码整体的误码性能，这也代表了采用内码编码所能实现的极限性能。虽然本文中所采用方案的性能与极限性能还有很大差距，但也在很大程度上提升了Polar码的性能。

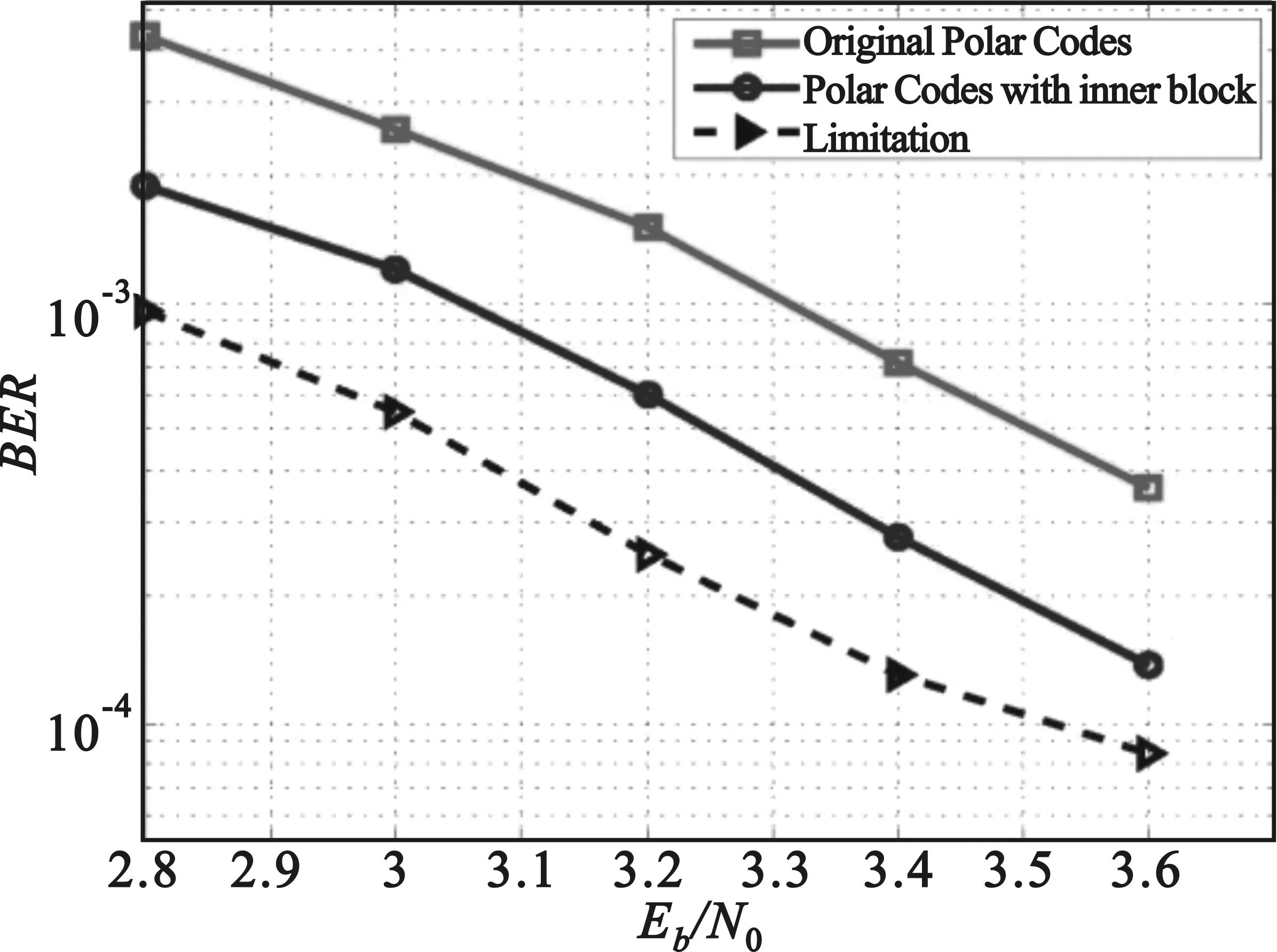
图4　性能仿真曲线

5结语

本文在Polar码的基础上进行内码编码形成两级串行级联的编码结构旨在通过利用原本冻结的比特信道对不稳定的信息位进一步约束，以提高不稳定信息位的可靠性，从而从整体上提升Polar码的性能。相比原码字级联编码后并未增加额外的冗余，其码长以及码率保持不变。本文以码长256，码率0.5 的Polar码为例进行了仿真，对特定信息位进行内码编码，并针对该级联结构采用了改进的译码算法，仿真结果显示整体性能提升约0.3 dB，且复杂度并没有明显提高。虽然性能提升的空间和幅度有限，但本文为提升Polar有限码长性能提供了新的思路并为将Polar码推向实际应用做出了贡献。

参考文献：

[1]Shannon C E.A Mathematical Theory of Communication.Bell System Technical Journal,1948,27(6): 379-423.

[2]王志文，徐以涛，江汉等.基于USRP平台的宽带频谱感知系统设计与实践[J].通信技术，2015，48(06):750-754.

WANG Zhi-wen,XU Yi-tao,JIANG Han,et al.Design and Implementation of Wideband Spectrum Sensing System Based on USRP Platform [J].Communications Technology,2015,48(06):750-754.

[3]Arikan E.Channel Combining and Splitting for Cutoff Rate Improvement [C].In Proc.of IEEE ISIT 2005,2005: 671-675.

[4]Arikan E.Channel Polarization: A Method for Constructing Capacity-Achieving Codes [C].In Proc.of IEEE ISIT 2008,2008: 1173-1177.

[5]Arikan E.Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels [J].IEEE Transactions on Information Theory,2009,52(2): 3051-3073.

[6]Peter Trifonov.Efficient Design and Decoding of Polar Codes[J].IEEE Transactions on Information Theory,2012,60(11):3221-3227.

[7]Proakis J G.Digital Communications[M].America: McGraw Hill,1995,175-176.

[8]Arikan E and Telatar E.On the Rate of Channel Polarization [C].In Proc.of IEEE ISIT 2009,2009: 1493-1495.

[9]Seidl M and Huber J B.Improving Successive Cancellation Decoding of Polar Codes by Usage of Inner Block Codes [C].In Proc.of 6thIS on TC& IIP,2010: 103-10.

An Encoding Algorithm for Two-Stage Serial Cascade Polar Codes

WU Dong-sheng,LIU Ai-jun,ZHANG Ying-xian,ZHANG Qing-shuang

(Communication Engineer College,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

Abstract：As the first channel correcting of code known to achieve the capacity of symmetric channels,polar code now becomes a hot research topic in coding,and what is more,the coding and decoding complexities of polar code are fairly low.However,on account of the restriction by polarizing speed,the polar code with finite length is worse than some existing codes in performance,such as LDPC and Turbo.For improving the performance of polar code with finite length,a cascade coding scheme based on two-stage polarization is proposed,and for this coding scheme,an improved decoding algorithm is also adopted,and the polar code with finite length thus raised in its performance.Simulation indicates that the polar code with finite length has an improvement of about 0.3dB in performance.The research result described in this paper could open an effective way for improving the performance of polar with finite length.

Key words：finite code length;systematic polar codes;two-stage polar codes;improved decoding algorithm

doi:10.3969/j.issn.1002-0802.2016.02.003

* 收稿日期：2015-09-01；修回日期：2015-12-16Received date:2015-09-01；Revised date：2015-12-16

基金项目：国家自然科学基金(No.61501508)

Foundation Item:National Natural Science Foundation of China (No.61501508 )

中图分类号：TN927.2

文献标志码：A

文章编号：1002-0802(2016)02-0135-04

作者简介：