Polar码并行级联结构设计及性能分析*

潘小飞，张青双，蔡　彪，成风毅

(解放军理工大学 通信工程学院，江苏 南京 210007)



Polar码并行级联结构设计及性能分析*

潘小飞，张青双，蔡彪，成风毅

(解放军理工大学 通信工程学院，江苏 南京 210007)

摘要：提出一种基于Polar系统码的并行级联结构，通过引入迭代译码过程，以提升有限码长Polar码性能。首先利用分组码的联合界技术，在均匀交织的条件下分析了所提级联码的码重分布特性，并给出了在中高信噪比下的渐近性能界。然后，利用分量译码器外信息转移图分析了不同码长Polar码并行级联的迭代收敛性能。仿真结果表明，在AWGN信道条件下，所提并行级联码性能优于相同码长、码率的系统Polar码，并且与理论分析结果匹配，证明了理论分析的有效性。

关键词：Polar系统码；并行级联；渐近性能；迭代收敛性能

0引言

Polar码是2009年，土耳其专家Arikan基于信道极化提出的一种新的信道编码方案，也是第一种在理论上证明能够达到Shannon极限的码字，近年来引起了信道编码、物理层安全等领域学者的极大关注[1-2]。虽然具有编译码复杂度低，Shannon极限可达等特点，但在有限码长条件下，Polar码与LDPC以及Turbo码相比，在性能上依然有一定差距。主要原因是信道极化速度较慢，在有限码长条件下，为保证较高码率传输，一部分信道条件较差的极化后的子信道也被选来传输信息，这样必然会导致误码性能恶化。

为解决此问题，许多基于Polar码的级联编码方案被提出，以辅助提高有限码长条件下Polar码性能。文献[3]将RS码与Polar以Turbo乘积码的方式级联以提高信道条件较差子信道的可靠度。文献[4]将文献[3]中的RS码替换为BCH码和卷积码，进一步提升级联性能。文献[5]将条件较差的子信道进行二次编码，通过引入LDPC码来提高相应子信道的可靠度。 实际上，任何线性分组码都可以转化为系统码的形式。上述文献均局限于非系统Polar的级联方案设计，并未考虑系统利用系统Polar码来设计迭代结构以探索更优性能。

1Polar码基本原理

1.1信道极化

对于两个独立的相同容量的逻辑信道，Arikan发现对信道进行组合和拆分以后，生成的两个子信道容量不再相同。一个信道的容量会增加，另一个容量则相应的减小，总容量则保持不变，这种通过模二加方式使信道容量发生变化的现象称为信道极化现象。

(1)

式中，⊗为kronecker积。整个Polar码的编码即可表示为：

(2)

1.2SC(Successive Cancellation)软输出译码算法

SC算法是Arikan提出的Polar码最原始的译码算法，也是复杂度最低的算法。

图1　N=8的Polar码因子图示例

然而，在迭代译码过程中往往需要软入软出(SISO)译码算法来实现软信息的交互，SC算法并不能完成这一功能。文献[6]利用SC译码的特点，设计了一种低复杂度的软输出SC译码算法(SCAN)。

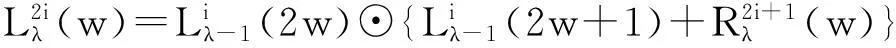
(3)

其中运算符号⊙定义为：

传统的教学多以教师讲授为主，以教师为主体，易于控制教学的进程，逻辑性和系统性相对较强，学生遵循教师的讲解，易于快速形成知识结构和体系．然而，这种教学方法不利于调动学生的积极性和主动性，学生的参与意识不强，因此需要改变授课方式．

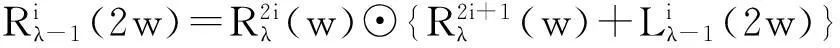
(4)

(5)

2并行级联结构设计

2.1SC软输出译码算法

Polar系统码和传统的系统码类似，在编码码字中包含所要传送的信息比特。可以对非系统码进行相应的变换，获得其系统码的形式[7]。将式(2)分解后可得：

(6)

(7)

式中，GAB为集合B确定的矩阵GA的列向量构成的矩阵。如果GAB为可逆矩阵，则极化后的子信道传输的信息为：

(8)

(9)

为保证GAB可逆，根据GN的特性，可将集合B与集合A取值相同，由此方式构造的Polar码即为系统码。

2.2基于Polar系统码的并行级联结构

由于Polar码本身的一些缺陷导致在有限码长时，误码性能并不理想。为提高有限码长性能，提出类似Turbo码的并行级联结构，如图2所示。

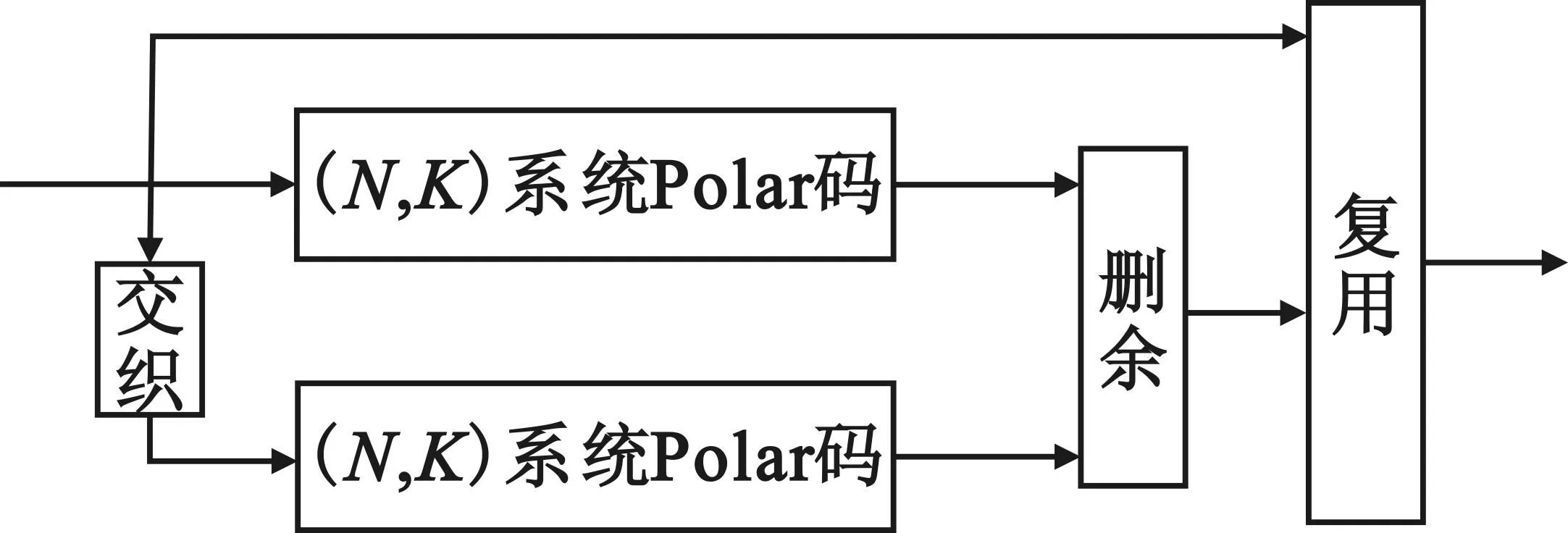
图2　Polar系统码并行级联结构

图2给出了基于Polar系统码的并行级联结构，类似与Turbo码，信息比特先经过Polar系统码编码形成第一路校验比特；然后再对交织后的信息比特进行二次Polar系统编码，形成第二路校验比特。两路校验比特经过删余后与信息比特共同构成级联码字。需要注意的是，Polar码为分组码，码长必须为2的幂次，在交织长度为M的情况下，可以将整个数据分为n=M/K个短的码组进行(N,K)系统码的编码，其中K为信息位长度。若每一个系统码分组校验比特的删余比特数为Cp，总码长为Nc=M+2n(N-K-Cp)，相应的级联码码率为：

(10)

该并行级联结构可以采用类似Turbo的译码方式，分量译码器采用SCAN译码算法，通过多次迭代以获得优异的性能。

3性能分析及仿真

为分析所提结构的的性能，以给码字的构造提供一定的理论指导，本节拟采用联合界技术对所提并行级联结构进行渐近性能分析。而后，利用外信息转移图来分析不同码长Polar码并行级联对系统性能的影响。

3.1渐近性能分析

(11)

式中，Ad表示码字集合中，码字重量为d的码字个数。相应的，其输入输出枚举函数可以表示为：

(12)

式中，Am,d表示输入信息比特重量为m，输出码字比特重量为d的码字个数。则相应的误码性能上界为[8]：

(13)

在高信噪比条件下，影响性能的只有最小码重的码字。对于并行级联的Polar码而言，在高信噪比条件下，性能上界仅和最小码重码字有关，即：

(14)

在采用均匀交织以后，相应码重码字的数量为[9]：

(15)

(16)

式中，M为交织长度。表1给出了(128,64)Polar系统码和(64,32)Polar系统码的码重分布，这两种码长码字的最小码重均为8。

表1　系统Polar码码重分布

由表1中数据可知，采用(128,64)的Polar码级联以后的最小级联码重为9，对应的信息序列重量为7。然而，信息重量大时，考虑交织的影响以后，其同时达到最小码重的概率极小，需要将相应较小的几个码重都考虑在内，即其误码性能渐近界为：

(17)

相应的，(64,32)码级联后的渐近性能为：

(18)

3.2收敛性能分析

上面仅仅估计了高信噪比时的信噪比渐近性能界，对于相同交织长度下，不同码长Polar码的迭代收敛特性并没有给一个很好的描述[10]。在分析Turbo码的收敛特性时，常采用外信息转移图(EXIT)来分析迭代收敛性能，对于并行级联Polar码也可以采用同样的方法来估计收敛特性[11]。假设SISO译码器的先验输入信息满足高斯分布，为：

(19)

(20)

利用该先验信息进行软输出译码以后，得到的外信息为E，则外信息与发送信息的互信息为：

(21)

即IE=T(IA,Eb/N0)，与输入先验信息和信道软信息有关。IA和IE的关系即为外信息转移图，通过该图即可观察某种Polar码的迭代收敛特性。

3.3仿真结果

基于前面的分析，本节对前面结果进行相应的仿真验证，信道条件为AWGN信道，采用BPSK调制。Polar系统码采用SCAN算法，迭代译码最大迭代次数为5次，Polar码构造方法采用密度进化算法[12]，且码率设置为0.5，级联码率为1/3。

图3给出了Eb/N0=1.2 dB，交织长度为40 960时，不同码长Polar码的外信息转移图对比；可以看出，在相同交织长度下，码长越长，收敛门限越高；然而相应的误码平层越低，原因是码长长，最小码重较大。

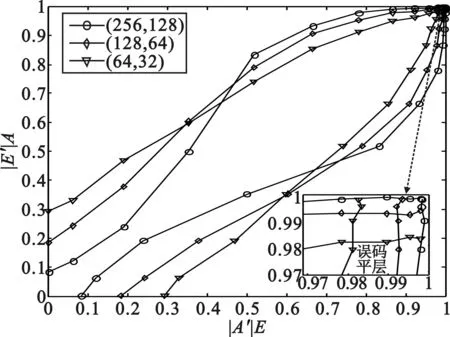
图3　Eb/N0=1.2 dB,交织长度40 960，不同Polar码并行级联迭代的外信息转移图对比

图4给出了不同码长Polar码在相同交织长度条件下的误比特率仿真结果对比，分量译码器采用SCAN算法，SCAN仅1次迭代，分量译码器之间的迭代次数为5次。由图中可以看出(64,32)Polar码收敛门限较低，误码平层较高，而相应的(128,64)Polar码收敛门限最高，误码平层最低，这和EXIT图分析结果一致。同时，可以看出，利用联合界技术分析的(128,64)Polar的渐近收敛特性和仿真曲线在高信噪比条件下基本一致，验证了分析的准确性。同时，在误比特率10-5条件下，若采用(128,64)并行级联，与相同码率，码长相近的系统Polar码相比，性能优势在0.5 dB左右。同时，并行级联结构的分量译码过程中，每个码块可以并行译码，译码延时相比于单独的系统Polar码而言，要低很多。

图4　交织长度1024，级联码率1/3,分量码率0.5，不同码长条件下误比特率仿真结果

4结语

本文提出了基于Polar系统码的并行级联结构，利用联合界技术和外信息转移图分别分析了所提结构的渐进性能和迭代收敛性能，AWGN信道下的仿真结果与理论分析相符合。与相同码长码率的系统码相比，性能提升0.5 dB，大大提高了Polar码的实用价值。为实现高码率的并行级联码，系统Polar码的删余设计需要进一步的研究。并行级联结构的收敛门限和误码平层需要一个折衷，在分量码长选定的情况下，需要深入研究合适的交织器来降低误码平层。

参考文献：

[1]Arikan E.Channel Combining and Splitting for Cutoff Rate Improvement [J].IEEE Transaction on Information Theory,2006,vol.52 (2):628-639.

[2]Arikan E.Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels [J].IEEE Transactions on Information Theory,2009,vol.55(7): 3051-3073.

[3]Mahdavifar Hessam,El-Khamy Mostafa,Lee Jungwon and Kang Inyup.Performance Limits and Practical Decoding of Interleaved Reed-Solomon Polar Concatenated Codes[J].IEEE Transaction.Communication,2014,62(5): 1406-1417.

[4]WANG Ying and Krishna R Narayanan.Concatenations of Polar Codes with Outer BCH Codes and Convolutional Codes[C]//.Proc.52-th Annual Allerton Conference,Monticello,2014: 813-819.

[5]GUO Jing,QIN Ming-hai,Albert Guillen i Fabregas and Siegel Paul H.Enhanced Belief Propagation Decoding of Polar Codes Through Concatenation[C]//.Proc.IEEE ISIT,Honolulu,2014: 2987-2991.

[6]Fayyaz Ubaid U and Barry John R.Low-Complexity Soft-Output Decoding of Polar Codes[J].IEEE Selected.Communication.,2014,32(5): 958-966.

[7]Arikan E Systematic Polar Coding[J].IEEE Communication.Letter,2011,15(8): 860-862.

[8]Benedetto S and Montorsi G.Unveiling Turbo Codes: Some Results on Parallel Concatenated Coding Schemes[J].IEEE Transaction.Information.Theory.,1996,42(2): 409-429.

[9]Chatzigeorgiou Ioannis and Rodrigues Miguel R D.Analysis and Design of Punctured Rate-1/2 Turbo Codes Exhibiting Low Error Floors[J].IEEE Selected.Communication,2009,27(6): 944-953.

[10]李斌,王学东,王继伟.极化码原理及应用[J].通信技术,2012,45(10):21-23.

LI Bin,WANG Xue-dong,WANG Ji-wei.Theory and Application of Polar Code[J].Communications Technology,2012,vol.45(10):21-23.

[11]Brink S Ten.Convergence Behavior of Iteratively Decoded Parallel Concatenated Codes[J].IEEE Transaction.Communication.,2001,49(10): 1727-1737.

[12]Trifonov Peter.Efficient Design and Decoding of Polar Codes[J.IEEE.Transaction.Communication,2012,60(11): 1-7.

Design and Analysis of Parallel Concatenation Structure for Systematic Polar Codes

PAN Xiao-fei,ZHANG Qing-shuang,CAI Biao,CHENG Feng-yi

(College of Communications Engineering,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

Abstract：A parallel concatenated structure based on systematic polar codes is proposed,thus to improve the performance of polar codes with finite length by using the iterative decoding strategy.Firstly,the union bounding technique is used to estimate the asymptotic performance for the proposed structure when uniform interleaver is considered.Then,the convergence behavior is analyzed by means of extrinsic information transfer chart (EXIT chart).Simulation results show that the proposed structure outperforms the systematic polar codes in same code length and rate.Meanwhile,the simulation results and theoretical results are well matched and this indicates the correctness of this theoretical analysis.

Key words：systematic polar codes; parallel concatenation; asymptotic performance; iterative convergence behavior

doi:10.3969/j.issn.1002-0802.2016.02.002

* 收稿日期：2015-09-06；修回日期：2015-12-21Received date:2015-09-06；Revised date：2015-12-21

中图分类号：TN911.3

文献标志码：A

文章编号：1002-0802(2016)02-0130-05

作者简介：

潘小飞(1979—)，男，博士，副教授，主要研究方向为低信噪比条件下信号的接收，信息论与编码；

张青双(1990—)，男，博士研究生，主要研究方向为信息论与信道编码，卫星通信；

蔡彪(1992—)，男，硕士研究生，主要研究方向为卫星通信；

成风毅(1988—)，男，硕士研究生，助教，主要研究方向为信息论与信道编码，卫星通信。