基于SARIMA模型的中国农产品价格指数短期预测

陈灿煌（湖南理工学院经济（七）管理学院，湖南　岳阳　414000）



基于SARIMA模型的中国农产品价格指数短期预测

陈灿煌
（湖南理工学院经济（七）管理学院，湖南岳阳414000）

摘要：本文以中国1999年1月～2014年12月的月度农产品价格指数作样本，运19.SARIM A（1，1，1）（1，1，1）12模型对农产品价格指数进行样本内静态预测和样本外动态预测。实证结果表明，模型的样本内静态预测效果比样本外动态预测效果理想，因此，该模型更适合于农产品价格指数的短期预测。

关键词：农产品价格指数；短期预测；SARIM A模型

一、引言

农产品价格频繁异常波动，不仅会引起社会整体物价水平的波动，从而影响到人民生活水平的稳定，而且还将给广大农产品生产者和经营者带来额外的市场风险，同时也给国家的宏观经济运行带来不稳定因素。因此，稳定农产品价格已经成为我国宏观经济调控的重要目标。通过运19.合理的方法对农产品价格的短期变动做出较准确的预测，以把握农产品价格总体水平的未来走势，可以为农产品生产者和经营者规避农产品价格波动风险、为政府平抑农产品价格波动提供预警和决策依据。

二、数据来源及预处理

（1）数据来源。本文所使19.的数据为1999年1月～2014年12月的我国农产品价格月度同比指数（上年同月=100），共192个数据，其中使19.1999年1月～2012年12月共168个数据进行建模，使19.2013 年1月～2014年12月的24个数据进行模型检验。将农产品价格指数的月度时间序列命名为API，由于该时间序列是以上年同月为基期计算得到的，本身已剔除了一部分季节因素，为了进一步减缓该序列的波动程度，使该序列平稳化以满足建模的条件，下文将对序列API进行预处理并19.该序列建模分析。使19.Eviews5.0软件进行分析。

（2）数据预处理。首先为了消除该时间序列数据可能存在的异方差，将该原始数据进行对数化处理，记为LnAPI。从我国的月度农产品价格指数对数化后的序列图（图1）可看出，尽管该月度数据已剔除了一部分季节因素，但两者仍然呈现出一定的上升趋势和季节性变化，为非平稳序列。

图1　农产品价格指数（LnAPI）时间序列图

为消除该序列存在的趋势性，对对数时间序列进行一阶逐期差分处理，经过差分后的序列命名为，经过初步判断，该差分序列是一个平稳序列。但是，在差分序列▽LnAPI1的自相关图（图2）中，滞后12阶的自相关系数明显超出了置信Ⅱ，显著不为零，说明时间序列LnAPI自带周期T=12的季节波动，吻合了样本采19.月度数据的事实。为消除原序列存在的季节变动，对逐期差分后的对数时间序列▽LnAPI1做步长为s= 12的季节差分，以更好地拟合样本数据。一阶逐期差分和季节差分处理后的序列▽12▽LnAPI无明显的趋势性，无巨大的波动；同时经逐期差分和季节差分后，该序列的自相关系数和偏自相关系数很快落入随机区间（图3），可以初步判断序列的趋势和季节性已经基本消除，成为平稳时间序列。

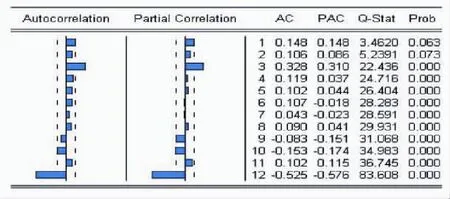
图2　▽LnAPI的自相关（七）偏相关图

图3　农产品价格指数逐期和季节差分（▽12▽LnAPI）的偏相关和自相关图

三、SARIMA模型的建立

SARIM A模型的建立主要包括四个步骤：模型的定阶（七）结构识别、模型的参数估计、模型的诊断（七）检验、模型的预测。因此，首先对季节数据的平稳性进行检验，如果季节数据是非平稳的，须进一步确认季节数据的单整阶数；然后正确判断（非）季节自回归多项式、（非）季节移动平均多项式的形式，以保证该模型平稳、可逆。

1.序列的平稳性检验

由上述时间序列图1可初步判断农产品价格指数（API）是非平稳的，但要更准确地判断该序列的平稳性，需要借助有关的检验法作进一步的检验。下面运19.ADF检验对农产品价格指数序列的平稳性进行检验。

表1　LnAPI、▽LnAPI、▽12▽LnAPI的单位根检验结果

单位根检验结果显示，原序列LnAPI是非平稳序列，而一阶差分处理后的序列▽LnAPI是平稳序列，因此LnAPI是一阶单整序列，即d=1。对一阶逐期差分和季节差分处理后的序列▽12▽LnAPI进行单位根检验，结果显示，▽12▽LnAPI序列是平稳的。另外，由于逐期差分序列经过一阶季节性差分后消除了该时间序列的季节性，故D=1。经过上述检验和处理，LnAPI序列满足了Box-Jerkins模型平稳的建模要求，允许建立季节调整的SARIM A模型。

2.模型的定阶（七）识别

（1）模型的定阶。由于上文确定了序列LnAPI的非季节差分阶数d=1；季节差分阶数D=1，故考虑建立SARIM A（p，d，q）（P，D，Q）12模型进行分析（七）预测。接下来确定p，q，P，Q的取值。利19.序列自相关图（七）偏相关图可看出，在滞后期为12时自相关系数、偏自相关系数两者均显著不为零，故模型中待估的季节参数取P=Q=1，以避免由于模型的过度拟合而影响其预测精度。

利19.自相关函数（七）偏相关函数的统计特性，可识别模型的p、q阶数。由图2可看出，▽LnAPI序列的自相关系数在3阶截尾，偏自相关系数同样在3阶截尾，其余大多落在随机区间以内。在建模过程中，应在滞后期P和q（七）模型的自由度之间找到一种均衡。p和q取得足够大，一方面能够全面反3.出模型中的所有相关动态信息，但另一方面，将使得模型的待估参数大大增加，从而自由度减小，导致估计方差的加大，增加了模型的复杂性和估计结果的不可靠性。综合考虑取p= 1，3（七）q=1，3进行参数估计。

（2）模型的识别。通过观察平稳序列的自相关和偏相关图，对可能性最大的SARIM A（1，1，1）（1，1，1）12；SARIM A（3，1，3）（1，1，1）12.；SARIM A（1，1，3）（1，1，1）12；SARIM A（3，1，1）（1，1，1）12进行比较评价。在选择模型时，一般根据AIC值和SC值最小的准则和修正的拟合优度R2最大的原则作出选择。

表2　各种拟合模型的参数比较

结合修正拟合优度R2（七）赤池信息准则（Akaike Inform ation Criterion，AIC）和施瓦茨准则（Schwarz Criterion，SC）具体数值（表2），对SARIM A（p，d，q）（P，D，Q）12的拟合效果进行比较，从而最终确定模型的阶数。显然，SARIM A（1，1，1）（1，1，1）12是相对更优的模型。

3.模型的参数估计

运19.Eviews5.0软件对模型SARIM A（1，1，1）（1，1，1）12进行参数估计，得到如下结果：

首先，从模型的t检验结果看，每一解释变量均显著不为零；其次，回归残差无自相关，能通过P检验；最后，模型的自回归多项式具备平稳、移动平均多项式具备可逆的特点。因而，该模型均可以接受。

4.模型的检验

上述模型的残差、实际值、拟合值（图4）初步证明了模型的拟合程度较高；图5表明，模型残差序列的相关图、偏相关图表明残差序列不存在序列相关。

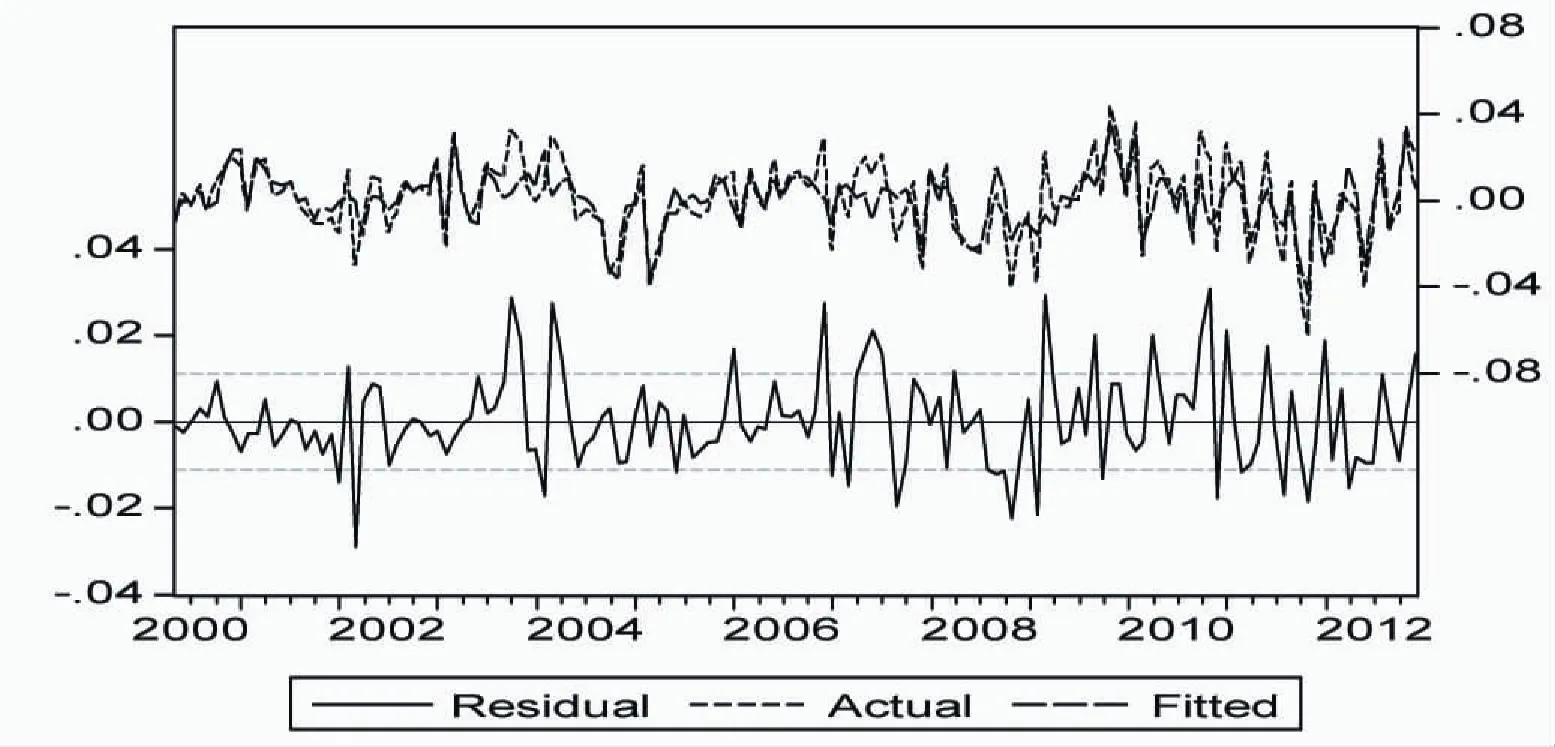
图4　SARIMA（1，1，1）（1，1，1）12模型真实值、拟合值、残差序列图

图5　SARIMA（1，1，1）（1，1，1）12模型残差序列的相关图、偏相关图

该模型是否适合预测需要作进一步检验。通过对SARIM A（1，1，1）（1，1，1）12模型的残差序列进行单位根检验，发现残差序列在1%显著性水平上通过了ADF检验，表明模型的残差序列是平稳的，因此，该模型拟合程度比较好，适合解释当前时间序列和19.来预测。

四、基于SARIMA模型的预测分析

根据建立的SARIM A（1，1，1）（1，1，1）12模型，对2013年1月～2014年12月共24个月的农产品价格指数进行静态预测，通过真实值（七）预测值的比较，判断模型的预测精度，然后再将2013年1月～2014 年12月的数据添加到原始序列中，利19.新的序列建立模型，对2015年1～9月的样本外观测值进行动态预测。静态预测结果见表3。

通过对表3的预测值（七）实际值比较可发现，二者基本上能保持相同的变动趋势，前24个月的平均相对误差为0.011，说明预测精度很高。同时，通过对预测误差指标的计算也可以发现，两个绝对误差指标：均方根误差（RM SE）为1.6386、平均绝对误差（M AE）为1.2752都很小；两个相对误差指标：平均绝对百分比误差（M APE）为1.2092，介于0～5之间；希尔不等系数（TIC）为0.0078，介于0～1之间，且远远小于1，这两项衡量指标很好地说明了该模型有较高的预测精度，能很好地拟合效果。预测值（七）真实值之间存在的偏差，可能是拟合模型建立过程中不可避免的误差所致。

以下运19.SARIM A（1，1，1）（1，1，1）12模型，对2015 年1～12月的农产品价格指数进行动态预测。预测结果见表4：在2015年，我国农产品价格指数不会呈现大幅度的波动。由于随着预测长度的增大，移动平均项逐步淡出预测模型，因此，它的长期预测效果不是很理想，动态预测误差比静态预测误差大。

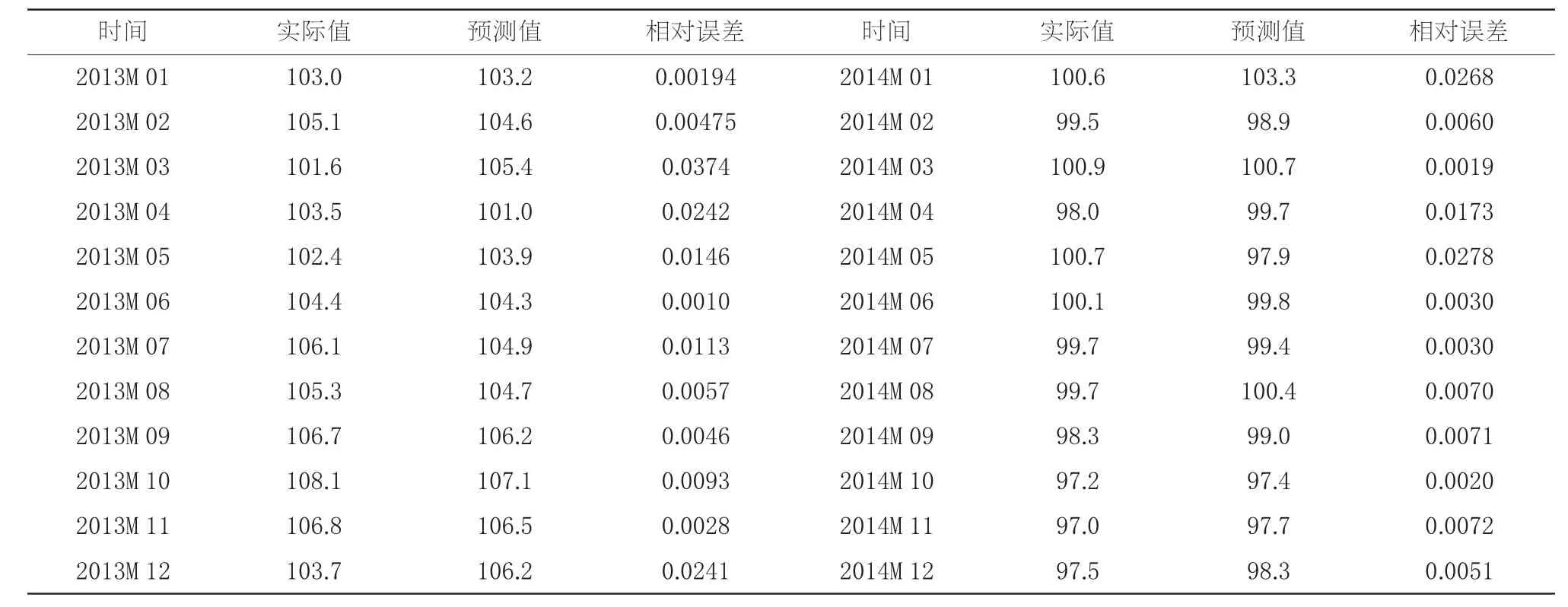
表3　农产品价格指数静态预测结果

表4　2015年1～12月农产品价格指数动态预测结果

五、结论

本文通过建立SARIM A模型，对我国1999年1月～2014年12月的月度农产品价格指数进行样本内的静态预测，对2015年1～12月份的农产品价格指数进行样本外的动态预测，得出了如下结论：

第一，SARIM A（1，1，1）（1，1，1）12模型的样本内静态预测表明，2013年1月～ 2014年12月的样本内预测值和真实值差距比较小，绝大多数月份的相对误差率控制在1%以内，证明模型拟合效果比较理想。

第二，SARIM A（1，1，1）（1，1，1）12模型的样本外动态预测表明，2015年1～12月我国的农产品价格指数将呈平稳波动的趋势；同时，随着预测步长的延长，预测误差逐渐增大。

第三，虽然SARIM A（1，1，1）（1，1，1）12模型简单、操作性强，拟合和预测效果理想，但该模型只是对单变量时间序列进行建模及预测，我们无法从模型结构中了解到有哪些因素以及这些因素是如何影响农产品价格；同时，从长期看，影响农产品价格的因素错综复杂且千变万化，加剧了农产品价格波动，因此，SARIM A（1，1，1）（1，1，1）12模型的短期预测结果可能更理想。在实际操作过程中，为避免预测精度的下降，随着预测步长的延长，可以运19.静态滚动方法，将新的观测值引入模型对其进一步修正，以期得到更高精确度的预测值。

参考文献：

［1］丁文娜，何Ⅰ成，刘长城.我国Ⅰ米价格波动趋势及短期预测［J］.价格理论（七）实践，2014（4）：83－84.

［2］方艳，马燕.我国大豆价格波动及其未来走势预测［J］.价格理论（七）实践，2014（6）：67－69.

［3］刘凤根，李坤欢，周驭舰.中国金融发展（七）碳排放的动态关系经验分析［J］.湖南商学院学报，2016（1）：79—88.

［4］平平，刘大有，杨博，金弟，方芳，马思佳，田野，王16..组合预测模型在猪肉价格预测中的应19.研究［J］.计算机工程（七）科学，2010（5）：109－112.

［5］陈兆荣，雷勋平，王亮，等.基于ARIM A-SVM组合模型的我国农产品价格预测研究［J］.财经经理论研究，2013（2）：103-107.

［6］张立杰，寇纪淞，李敏强，朱新杰.基于自回归移动平均及支持向量机的中国棉花价格预测［J］.统计（七）决策，2013（6）：30－33.

［7］张敏.中国通货膨胀成因（七）结构动态的经验分析［J］.湖南商学院学报，2016（1）：89-96.

（责任编辑：杨粤芳）

On Short-term Prediction of Agricultural Prices Index of China Based on SARIMA Model

CHEN Can-huang
（H unan InstituteofScienceand Technology，Yueyang，H unan 414000）

Abstract：This paper employs SARIMA（1，1，1）（1，1，1）12Model to do the static and dynamic prediction for agricultural prices index inside and outside the sample respectively based on the monthly dating of agricultural prices from January，1999 to September，2014 in China. As is shown in the empirical results，the effect of the static prediction is more ideal than that of the dynamic one. Therefore，the SARIMA（1，1，1）（1，1，1）12 model is more adequate for the short-term prediction on agricultural prices index.

Key words：agricultural prices index；short-term prediction；SARIMA Model

中图分类号：F323.7

文献标识码：A

文章编号：1008-2107（2016）02-0016-05

收稿日期：2016－01－11

基金项目：国家社会科学基金项目（项目编号：11BJY117），国家社会科学基金项目（项目编号：14CJY056）的阶段性成果。

作者简介：陈灿煌（1964—），男，湖南汨罗人，经济学硕士，湖南理工学院经济（七）管理学院副教授。