考虑卷积完全匹配层数值色散的井间电磁三维正演

方思南， 潘和平*， 杜婷， 王智， 邓呈祥

1 中国地质大学(武汉)地球物理与空间信息学院， 武汉　400074 2 湖北煤炭地质勘查院，武汉　430070

考虑卷积完全匹配层数值色散的井间电磁三维正演

方思南1， 潘和平1*， 杜婷2， 王智1， 邓呈祥1

1 中国地质大学(武汉)地球物理与空间信息学院， 武汉400074 2 湖北煤炭地质勘查院，武汉430070

摘要本文将以卷积完全匹配层为吸收边界条件的时域有限差分法应用到井间电磁的三维正演模拟中. 证明了卷积完全匹配层中的数值色散会因为有效延伸因子而产生，列举常规有效延伸因子和网格间距对电磁波相速度各向异性的影响，并通过波场快照验证卷积完全匹配层中数值色散的存在；进而推广三维卷积完全匹配层中最大有效延伸因子、最大网格间距与激励源主频之间的约束，以此完善卷积完全匹配层的最优参数设置方案. 在此基础上，通过正演结果中二次场的垂直磁场分量和走时来展示灵敏度分布，以此划定井间电磁勘探的优势区域，提出井间电磁正反演所需要的约束测井系列和最佳取井方案.

关键词井间电磁(CWEM)； 三维正演； 时域有限差分(FDTD)； 卷积完全匹配层(CPML)； 数值色散

1引言

随着现今油气新区的勘探难度加大，油气勘探方向越来越多的聚焦在已经进入到开发中后阶段的油田上，这就需要更加准确地获取井间的地层构造、储层分布和油气运移等信息.井间电磁(Cross-Well Electromagnetic，CWEM)法，因其能低成本、高效率地完成数据采集工作，能通过反演电阻率来定量评价储层的含油性，能将高丰度的一维测井信息延展到三维储层空间中(沈金松等，2014)，能通过与地震数据联合反演来监控储层动态信息(Carcione et al.，2012)，所以可以胜任油田二次开发的勘探要求.

石油勘探中井间电磁成像系统的发展，由20世纪90年代的先导性理论研究(Newman，1995；Wilt et al.，1995)，到EMI公司生产的XBH-2000系统(曾文冲等，2001)，再到近年Schlumberger公司改进的Deeplook-EM系统(Al-Ali et al.，2009)，其中，Deeplook-EM井间电磁成像系统采用主要发射频率为5～1000 Hz的磁偶极子发射线圈，和灵敏度达到10-6nT的阵列接收线圈.在井间距确定的情况下，井间电磁的最大发射频率主要受套管、地层电阻率、发射线圈功率和接收线圈灵敏度的限制.

现阶段关于井间电磁的数值模拟研究主要集中在金属套管的影响规律(魏宝君等，2014)和理论模型的正演响应(Maclennan et al.，2014；Donadille and Al-Ofi，2012)方面，本文主要关注的是时域有限差分(Finite-Difference Time-Domain，FDTD)法在三维井间电磁波正演中的应用.

由于目前井间电磁勘探的最大井间距约900 m(沈金松等，2014)，纵向分辨率受发射频率、地层电导率的影响，通常为井间距的2%～5%(Alumbaugh and Morrison，1995)，而常见储层的厚度通常在10 m以内，加上井周3 m范围内的地层电阻率受泥浆侵入影响严重，故针对井间电磁正演的时域有限差分需要在小区域、小网格中进行，而这与低频电磁波中较大的趋肤深度相矛盾.因此，低频井间电磁波正演的关键问题是使吸收边界在靠近目标体的同时还能通过小网格来吸收低频电磁波.

在常规PML(Perfectly Matched Layers)的基础上(Bérenger，1994，1996；Chew and Weedon，1994)，具有严格因果关系、对低频波有较好吸收效果的复频移完全匹配层(Complex Frequency-Shifted Perfectly Matched Layers，CFS-PML)被提出来(Kuzuoglu and Mittra，1996)，CFS-PML可以被设置到紧邻目标体的位置以减少网格、节省内存，可以保证迭代后期的反射较小(Bérenger，2012)，可以对某一频率范围内的电磁波做最强吸收，因而被成功地应用到低频电磁波的正演中(李展辉和黄清华，2014).本文采用的卷积完全匹配层(Convolutional Perfectly Matched Layers，CPML)算法(Roden and Gedney，2000)，是CFS-PML的一种成熟有效的执行方法，具有非常广阔的发展前景(Bérenger，2007).

目前关于CPML优势吸收频率的研究比较深入(Bérenger，2012)，而关于CPML网格数值色散的研究刚刚起步(de la Kethulle de Ryhove and Mittet，2014)，且主要对一维网格间距要求做的理论推导，并未考虑CPML所在的三维坐标延伸空间，本文重点分析三维CPML中数值色散的来源、现象和限制方案.

2CPML的最优参数

CPML算法基于坐标延伸的麦克斯韦方程组，通过平面波在任意两层介质分界面上的零反射条件来提供本构参数的约束关系.

2.1含CPML的FDTD时域方程

频率域含 CFS-PML的无源麦克斯韦旋度方程(Bérenger，2007)中，常规三维欧几里得空间的拉普拉斯算子因为CFS-PML中的坐标延伸因子而被改写为一般形式(Chew and Weedon，1994)，如e分量(电场分量)v方向(v=x,y,z)的坐标延伸因子sev可写为(Kuzuoglu and Mittra，1996)：

(1)

其中，αev是电场在v方向的坐标延伸因子的自由度，σev是CFS-PML中的电导率，κev是有效延伸因子(Bérenger，2007)，ε是背景场的介电常数.

另外，麦克斯韦方程变换到时域中会因为坐标延伸因子而产生卷积项，如式(2)为时域变换后正演区域和吸收边界通用的Ex离散形式(Elsherbeni and Demir，2009)：

(2)

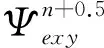
(3)

其中，

(4)

(5)

CPML中Ex的更新方程(式(2)—式(5))可以进一步推广到Ey、Ez、Hx、Hy、Hz，在常规FDTD(Elsherbeni and Demir，2009)的基础上，CPML对电磁波的吸收效果主要受αuv、σuv(Bérenger，2012)和κuv(u=e,m，v=x,y,z)的影响.结合前人对于αuv、σuv的深入研究(李展辉和黄清华，2014；Bérenger，2012)，本文重点关注CPML中κuv的数值色散问题，并讨论最优参数的选取方案.

2.2α影响CPML的吸收频率

参考式(1)，可以设置CPML的特征频率fav为(Bérenger，2012)：

(6)

通常在CPML算法中，设置平行于CPML法方向上的参数αev、αmv由CPML内边界的αmin线性变化到CPML外边界的αmax，以保证某一频率范围内的入射波能够被均匀吸收(Elsherbeni and Demir, 2009)：

(7)

其中，l为从CPML内边界开始数的网格层数，L为CPML从内边界到外边界的总层数.那么，对于α的设置，应先结合式(6)中入射波的频率范围，来确定αmin和αmax，再通过式(7)来计算CPML中各层的αev和αmv.

2.3σ影响CPML的吸收效率

电导率σev和导磁率σmv直接影响CPML对电磁波的吸收效率：σev、σmv过小会降低CPML的吸收效率，过大会在CPML的层界面上产生显著的反射(Bérenger，2012).在设置平行CPML法方向的σev和σmv时，采用式(8)来赋值最能提升CPML的吸收效率：

(8)

其中，幂m可以取2、3、4；σeb为背景场电导率，若背景场为真空环境，则令σeb=αmin；最外层CPML电导率σmax=ξσeb，可以取比例系数ξ<10.

2.4κ影响CPML的数值色散

与关注度较高的α和σ不同的是，目前CPML中κ的影响还没有学者重点关注过，直观的理解是，κ造成CPML的网格坐标延伸，那么与电导率的作用一致，κ越大吸收越强烈.但在正演实验中，我们发现当κ大于某一范围后，外侧CPML会产生持续的、震荡的干扰波，这是典型的数值色散特征.根据这一发现，本节推导由κ产生的数值色散的原因，并给出差分近似后相速度的各向异性关系，以期研究控制数值色散的方法.

平行于CPML法方向上的κuv由式(9)给出(Elsherbeni and Demir, 2009)：

(9)

其中，κmax为CPML最外层的值，通常可以取5～11(Roden and Gedney，2000).

综合式(7)、式(8)和式(9)可以发现，CPML中的参数都是以垂直于边界的坐标为轴对称分布，因此对于三维CPML而言，我们可以简化考虑二维情况下的数值色散问题.这里以垂直于y坐标的CPML为研究对象，采用TE波从垂直于z坐标的各个角度入射，此时所有电场对于z坐标而言都是横向电场，即构成TEz模式，不难推导TEz模式在自由空间中的平面波解：

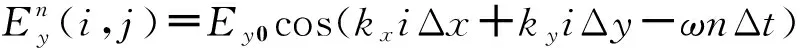
-ω(n+0.5)Δt).

(10)

再由式(2)推导出CPML中TEz模式的二维离散麦克斯韦方程组，如式(11)所示(由于在垂直于y坐标的CPML中，κex和κmx的值为1，Ψeyx、Ψmzx的值为0，所以这里直接给出简化后的结果)：

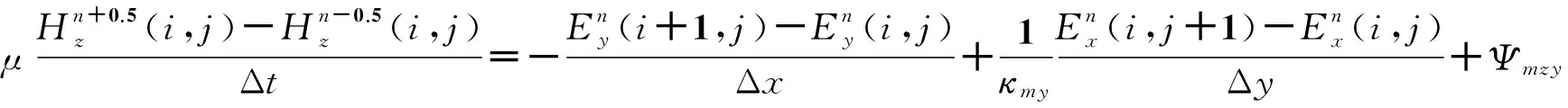
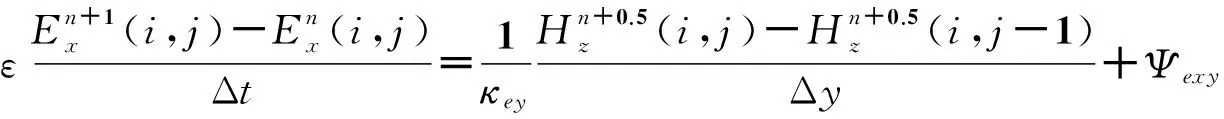
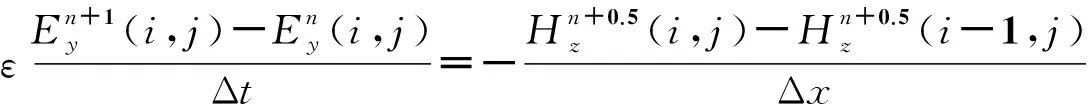
(11)

将TEz模式的平面波解式(10)代入式(11)中，结合三角恒等式：

cos(p-q)-cos(p+q)=2sinpsinq,

(12)

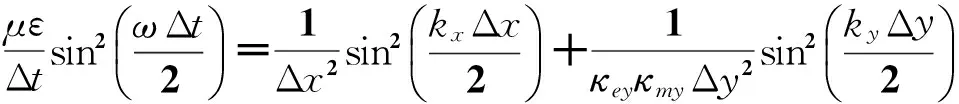
(13)

正是因为κ的影响，造成CPML中的二维数值色散关系与常规FDTD的不同.为了更直观地表现这种数值色散现象，进一步令常规网格均匀剖分Δx=Δy=δ，波矢量满足：

(14)

(15)

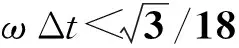
(16)

CPML数值色散关系的最终表达式(式(16))说明TEz模式平面波的相速度vφ与θ、λ/δ、κ有关，将此关系绘制成二维情况下的极坐标图(图1)，若图中θ=0°方向代表的是y方向，θ=90°方向代表的是x方向，那么图1可以理解为某一层的CPML介质垂直于y方向平铺，平面波可以从圆弧上的任意方向入射.图1a限定λ/δ=100，以κ为参变量，给出相速度与光速之比vφ/c与入射角θ之间的关系；图1b限定κ=2和κ=5，以λ/δ为参变量，给出vφ/c与θ之间的关系.

图1a中设置的λ/δ=100条件，保证了来自均匀网格的FDTD的数值色散非常小，在θ=90°方向上，vφ/c=1，而随着κ的增大和θ的减小，数值色散不断加剧，且在θ=0°方向近似呈vφ/c=1/κ的关系.图1b主要反映λ/δ对数值色散的影响：引起常规网格数值色散的因素在CPML中也适用，若λ/δ<10则会因为网格间距过大在各个方向产生不可忽略的数值色散；在λ/δ增大到10了之后，继续减小网格间距不会对κ造成的数值色散产生明显的影响，剧烈的色散现象在θ=0°方向依然存在.

因此，CPML中κmax的选择需要兼顾吸收效率与高频色散：当激励源主频较高时趋肤效应强烈，为了减小数值色散可以令κmax取较小值；当激励源主频较低时CPML的吸收效率也会降低，可以在增大网格间距的同时令κmax取较大值.

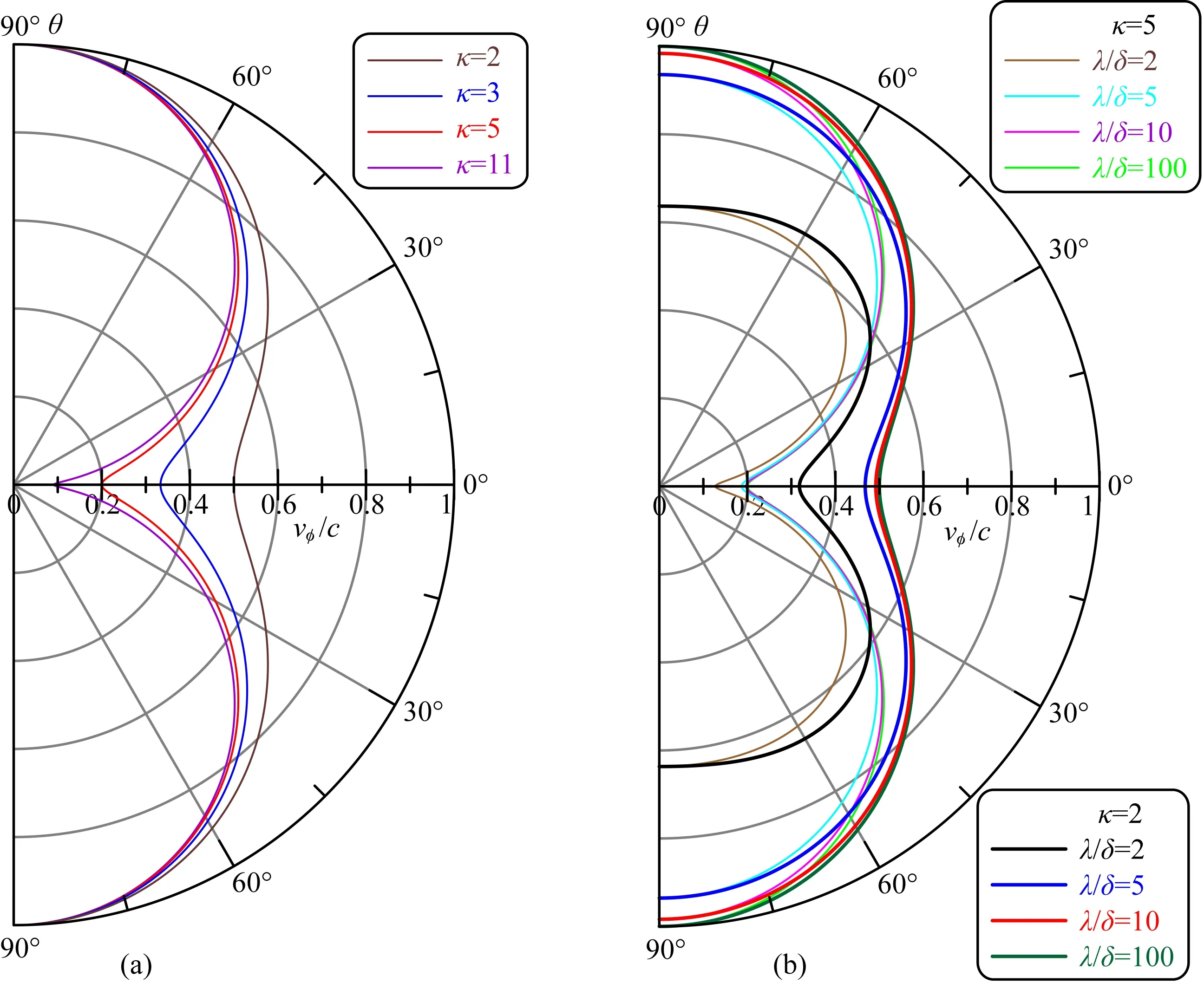
图1　CPML差分近似后vφ/c的各向异性关系(a) λ/δ=100时，vφ/c与θ、κ的关系；(b) κ=2和κ=5时，vφ/c与θ、λ/δ的关系.Fig.1　The anisotropy of vφ/c after difference approximate in CPML(a) While λ/δ=100, the relationship between vφ/c and θ, κ; (b) While κ=2 or κ=5, the relationship between vφ/c and θ, λ/δ.

2.5CPML的最优参数讨论

在CPML介质中因为κ的存在，数值色散也必然存在，依照式(9)的κ分布原则，预估数值色散主要发生在CPML的外层，而最内层的vφ/c接近于1.又由于吸收边界的目的是保证最终反射回内部正演区域的电磁波在一定百分比(γ)以内，所以对CPML的数值色散要求反而不用像内部区域中那样严格，只需要保证外层CPML中的因数值色散而产生的高频震荡波被内层CPML吸收即可，这也解释了为什么通常式(7)中的αmin取较大值的原因.

为了验证这一参数设置原则的可行性，并佐证CPML中数值色散的存在及影响因素，首先在网格步长为2 m的均匀三维真空空间中做高频正演实验：在内部区域中设置磁偶极子源，并发射截断三余弦脉冲，脉冲的最大发射频率接近均匀网格数值色散条件的最大频率，这样在限制常规网格的数值色散同时，突出坐标延伸网格的数值色散影响.采用的截断三余弦脉冲源较时谐场源和高斯脉冲源而言，在脉冲的两个端点处对时间的前五阶导数都为零，具更好的起始和终止时刻的波形平滑性，从而使其脉冲频谱更加接近理论值，也就能更好地控制因为源的接入而附带的高频成分，这一点对于会产生数值色散的CPML而言非常重要.外部区域以32层CPML和1层理想电导体(Perfect Electric Conductor，PEC)为吸收边界，用以展示CPML中电磁波相速度的变化规律.并按照式(6)提供的关系，用截断三余弦脉冲源的脉冲底座宽度(如2×10-7Hz-1)来计算CPML中的αmin和αmax，这样可以对比不同的内层CPML的αmin对外层CPML的数值色散的抑制作用.

图2为o((a1)—(a4))、p((b1)—(b4))、q((c1)—(c4))三种CPML的参数设置方案在1～4时刻的Hz波场快照，xy平面与发射线圈在同一平面上，z轴和色标均表示Hz的幅值大小.实验中，o和p参数设置主要是为了比较不同αmin对高频反射波的吸收效果，o和q参数设置主要是为了比较不同的κmax产生的数值色散效果.

图2(a1)—(c1)所在的时刻，截断三余弦脉冲已经完成发射，电磁波刚刚进入内层CPML，此时未发生明显的吸收边界反射，且三种参数设置对应的波场完全一致.

图2(a2)—(c2)所在的时刻，电磁波的波阵面进入到外层CPML，此时(c2)在吸收边界内的波场与(a2)、(b2)有较大的差异：一方面在电磁波入射角较小的外层CPML处出现了较明显的数值色散，而(c2)中数值色散范围更广、幅值更大，说明数值色散主要发生在入射角较小的CPML区域中，且κ越大数值色散越严重，这与图1a中的vφ/c随θ和κ变化的规律相呼应；另一方面(a2)、(b2)的波阵面要比(c2)更靠近PEC，这在图3b中表现的很明显，图3b是离CPML外边界距离为4 m的网格处的Hz正演结果，不难发现电磁波的传播速度在o、p两种参数条件下一致，且比q参数条件下要快，这说明了电磁波的传播速度主要受κ的影响，且κ越大vφ越小，这也证明了图1a中κ与vφ/c的关系的正确性.

图2　在与发射源同一深度平面上，CPML吸收效果的波场快照其他参数不变的情况下，(a1)—(a4)的参数设置为κmax=5、αmin=8.4×10-4、αmax=2.8×10-4； (b1)—(b4)的参数设置为κmax=5、αmin=2.8×10-4、αmax=8.4×10-4； (c1)—(c4)的参数设置为κmax=11、 αmin=8.4×10-4、αmax=2.8×10-4.其中，(a1)—(c1)的时刻为0.48×10-6s； (a2)—(c2)的时刻为0.74×10-6s； (a3)—(c3)的时刻为1.11×10-6s； (a4)—(c4)的时刻为1.39×10-6s.Fig.2　The snapshot of absorption effect in CPML in the same depth of emission sourceIn the condition that other parameter remain stationary, the parameter settings of (a1)—(a4) are κmax=5, αmin=8.4×10-4, αmax=2.8×10-4; the parameter settings of (b1)—(b4) are κmax=5, αmin=2.8×10-4, αmax=8.4×10-4; the parameter settings of (c1)—(c4) are κmax=11, αmin=8.4×10-4, αmax=2.8×10-4. And the time of (a1)—(c1) is 0.48×10-6s; the time of (a2)—(c2) is 0.74×10-6s; the time of (a3)—(c3) is 1.11×10-6s; the time of (a4)—(c4) is 1.39×10-6s.

图3　Hz在o、p、q三种参数设置中随时间分布图对应到图2中的坐标，这里(a)为(100, 40)点处的正演结果，(b)为(100, 4)点处的正演结果.Fig.3　In three parameter settings as o, p, q, Hz varying over timeCorresponding to the coordinate in Fig.2, (a) is the forward solution in (100,40), and (b) is the forward solution in (100,4).

图2(a3)—(c3)所在的时刻内，由内部区域辐射到CPML中的电磁波已经被大部分吸收，但在外层CPML内Hz的幅值依旧很大，这种波阵面已经离开该FDTD网格而电磁场分量依旧不断震荡的现象是典型的数值色散.若此处的网格处于真空环境中，则电磁场分量会呈指数上涨；这里三种参数设置中，外层CPML的电导率相同，电磁波的吸收过程会与数值色散形成某种动态平衡，则此时Hz的幅值可以作为衡量数值色散大小的标准.较(a3)而言，(b3)中Hz的幅值较大，说明内层CPML的αmin取较大值对于数值色散的抑制作用更强；(c3)中Hz的幅值较大且色散范围更广，因数值色散产生了明显的反射波，且CPML中κ越大数值色散产生的区域越靠内层，这都与图1a中的结论相一致.

图2(a4)—(c4)所在的时刻内，数值色散在被CPML压制的同时也遗留下了明显的反射波，其中(a4)外层CPML的数值色散被压制的最小.结合图3a中内层CPML处Hz的正演结果，发现p参数条件下高频色散波的吸收情况较差，而q参数条件下的高频色散波出现的较早，这也再次佐证了前面的结论.

总之，图2和图3都说明了CPML网格比常规均匀网格的数值色散要求要高，αmin设置为较大值能在一定程度上提升CPML对数值色散的抑制效果，但无法从根本上解决因为κ而生成的数值色散问题.

虽然根据图1b中的结论，网格间距在δ<λ/10以后继续减小不会显著改善外层CPML的数值色散，但是CPML中的数值色散出现的同时意味着电磁波相速度vφ的减小，这会从高频色散波的吸收效率的角度影响到CPML的吸收性能.结合各向同性介质中针对一维PML的垂直网格间距δ的限制要求(de la Kethulle de Ryhove and Mittet，2014)：

(17)

其中，γ>0为数值色散带来的电场或磁场误差，这里可以取γ=1%；m为电磁波在CPML中传播的总距离与趋肤深度S(ω)的比值，通常取小于2的值；cσ为电磁波在CPML中的传播速度；Δt为满足Courant稳定性条件的时间步长.

将式(16)在垂直入射情况下的vφ代入式(17)，我们可以进一步将垂直网格间距要求推广到三维CPML中：

(18)

其中，c0为真空中的光速，ω为电磁波的角频率.通过式(18)一方面可以限定网格间距δ的大小，另一方面可以在δ确定了的同时，通过γ来约束κmax.

综合以上论述，选择CPML的最优参数时，首先应该选择起止时刻波形平滑的激励源以减少源在接入时刻产生高频电磁波，然后考虑激励源的频谱区间fmax和fmin，根据式(6)分别计算αmax和αmin，再考虑激励源主频的大小，通过式(18)来确定κmax和δmax，根据背景场电导率来给出σmax，最后参考正演结果的数值色散情况反馈调整κmax.在本节实验γ相同的情况下，按照CPML最优参数设置方案，能增大43倍的网格间距，减少1/4时间节点，最终提升正演计算速度两百多倍.

3井间电磁的数值模拟及讨论

本文的正演模拟主要关注井间电磁波法的优势探测区域.根据法拉第定律，接收线圈处的垂直磁场分量Hz与感应电压成正比，在发射电流相同的情况下也与电阻抗成正比(Donadille and Al-Ofi，2012).因此，为了突出三维全空间中各网格的灵敏度分布，将单网格大小的高阻体或低阻体逐次嵌入到正演区域的网格中，并采用2.5节讨论的CPML最优参数分别进行正演；令正演结果中异常体引起的垂直磁场分量为Hzd=Hza-Hzh(Hza为有高阻体或低阻体情况下接收线圈处的垂直磁场分量，Hzh为均匀全空间情况下接收线圈处的垂直磁场分量)，并将Hzd作为评价井间电磁波优势探测区域的标准.

3.1异常体电导率的影响

设置含CPML的FDTD总计算区域为400 m×200 m×200 m，均匀网格间距为8 m，CPML占据外部的8层网格.图5所示为FDTD内部区域，其中发射探管所在直井的xy坐标为(128, 96)，接收探管所在直井的xy坐标为(272, 96).

首先讨论异常体电导率的变化Δσ对Hzd的影响：设置发射线圈坐标(128,96,96)，接收线圈坐标(272,96,104)，取背景电导率为0.02 S·m-1，并将单个网格大小的异常体设置到(200,104,104)处，异常体电导率在0.01～0.024 S·m-1之间变化.

如图4所示为七次FDTD的正演结果，当发射线圈采用三余弦脉冲时，接收线圈处的Hzd的波形接近正弦波波形.由于仅仅是异常体电导率的变化不会引起Hzd的相位变化，故每一条曲线均会在T1和T2时刻达到极值，且T1时刻对应三余弦脉冲源的极大值所在的时刻，T1时刻Hzd的幅值大于T2时刻.统计正演计算的结果，每条曲线均有Hzd(T1)∶Hzd(T2)=-1.23，以及参考感应测井几何因子理论(张庚骥，1982)的拟合关系式Hzd(T1)=-18.099Δσ3+0.931Δσ2-0.052Δσ.这表明了井间电磁的测量灵敏度与异常体电导率的相对变化量正相关；那么在井间电磁波的三维正演中，可以用Hzd(T1)来代表异常体二次场的振幅，用T1来代表异常体二次场的相位.这样一方面可以精简反演中的观测数据，又一方面可以将正演截断时间设置到三维空间中的最大T1之后，从而提升2倍以上的正反演速度.

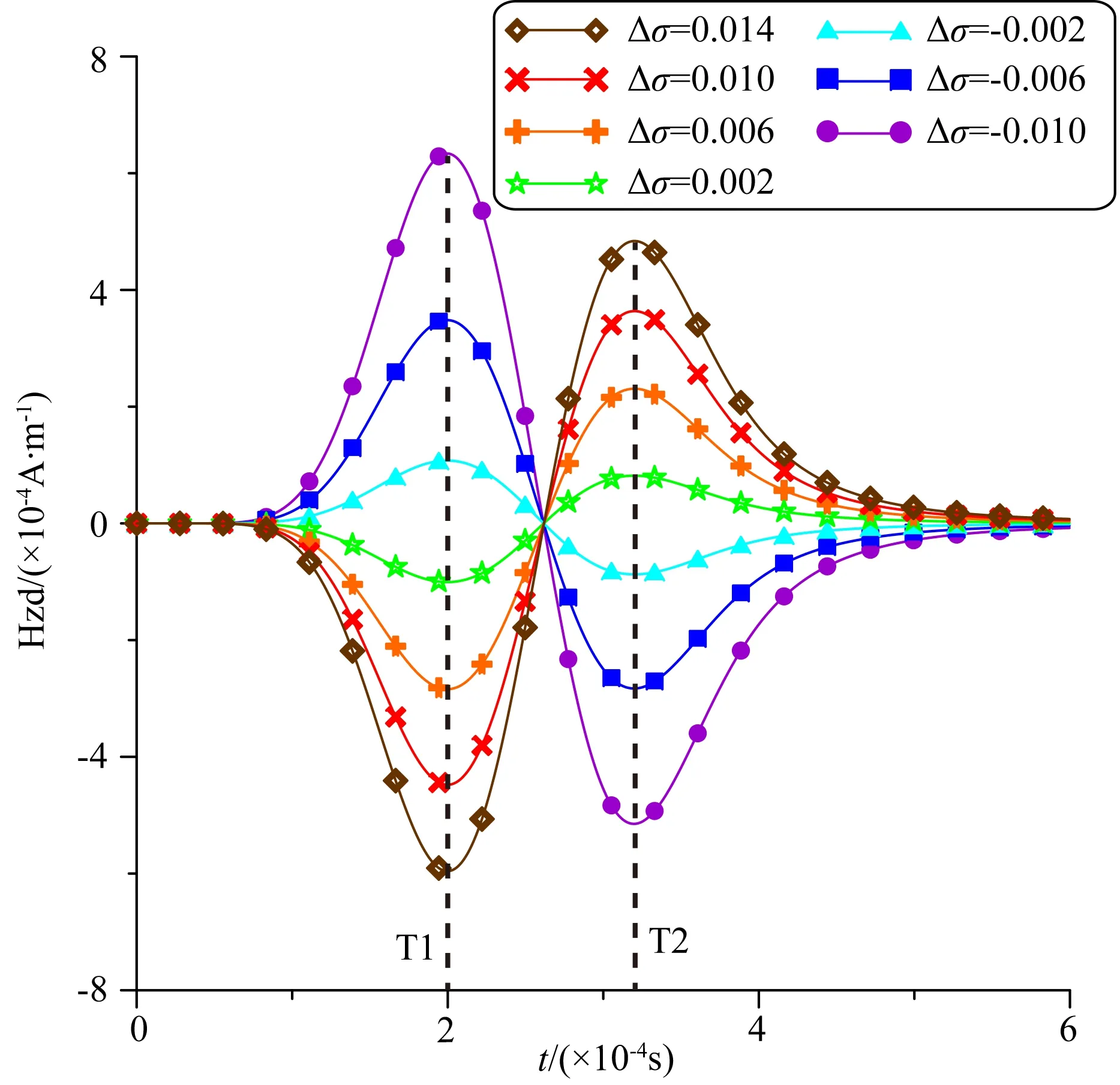
图4　电导率渐变的异常体在发射线圈、接收线圈中间时，Hzd随时间的变化曲线Fig.4　Hz varying over time while anomalous grid′s conductivity changes nearby the middle of transmitter coil and receiver coil

图5　高阻体的二次场的Hzd(T1)在三维空间中的分布图井轴上黑色圆环代表发射和接收线圈，(a1)、(a2)、(a3)分别为接收线圈的z=88、104、120时的Hzd(T1)，(b1)、(b2)、(b3)分别为接收线圈的z=88、104、120时的T1.Fig.5　Hzd(T1) of high resistance′s secondary field in three-dimensional spaceThe black circle in well axis means transmitter coil and receiver coil, (a1), (a2), (a3) is Hzd(T1) correspond with z=88,104,120, and (b1), (b2), (b3) is T1 correspond with z=88, 104,120.

3.2异常体位置的影响

基于图4的认识，在接下来的异常体位置的变化对Hzd的影响的讨论中，我们只需要分析全空间中Hzd(T1)和T1的值即可.令电导率为0.01 S·m-1的高阻网格在背景电导率为0.02 S·m-1的三维内部区域中移动，每移动一次做一次三维正演，将高阻网格所在的位置作为x、y、z，将每个高阻网格对应的正演结果中接收线圈处的Hzd(T1)和T1分别作为图5a和图5b中的色标，可以得到如图5所示的三维分布图.

从图5(a1)—(a3)中可以看出，Hzd的灵敏度分布整体上为椭球体(幅值相对较大的红、橙、蓝、紫区域)，且长轴在收发线圈的连线上.井间内侧区域的Hzd为正值，外侧区域的Hzd为负值；Hzd的灵敏度与该位置到接收、发射线圈距离的乘积近似呈负相关.需要注意的是，在x方向上，高阻体在临近线圈的内侧区域和外侧区域分别产生了Hzd的极大值和极小值，在y方向和z方向上却都接近零值，而靠近井轴的区域恰巧是泥浆侵入严重的地层，地层电阻率的空间变化相对复杂.因此，在井间电磁的正反演研究中，可以在收发线圈附近加密网格以实现井周复杂地层的精细描述，也可以结合阵列感应测井或电阻率测井的泥浆侵入信息，和声电成像测井或地层倾角测井的地层剖面信息，来提供线性化反演的初值及约束.

相比Hzd而言，三维空间中T1的灵敏度分布要简单很多，图5(b1)—(b3)中T1最小的位置都在收发线圈的连线上，且T1的空间等势面呈椭球体向外逐渐增大；从T1的颜色标尺上看，井间内侧区域的T1梯度较小，外侧区域的T1梯度较大，说明T1能够更好的提供外侧区域的二次场走时信息.

由于T1只受异常体位置的影响，灵敏度在井间外侧区域较大，而Hzd同时受异常体电导率和位置的影响，灵敏度在靠近接收线圈或发射线圈的区域较大，故井间电磁反演中T1贡献了更多异常体位置的信息，Hzd贡献了更多异常体电导率的信息.为了通过T1来反演异常体的位置，最好的方案是在接收、发射井的斜交方向上再做一组井间电磁观测，结合两口接收井中的T1信息，理论上就能通过三个椭球体等势面的交点确定异常体的位置.而在油田生产中，对于在目标储层内相距较近三口井不容易找到的情况，可以退而求其次，选用两口并不平行的井段(如斜井段和直井段)，同样可以实现异常体位置的标定.

4结论与建议

针对井间电磁勘探中发射频率低、网格间距小、计算区域小的情况，采用CPML作为FDTD的吸收边界条件，为了发挥CPML的低频吸收优势，本文首先就CPML的最优参数选择做了讨论，然后将其应用到井间电磁正演中，得到结论为：

(1) 在影响CPML吸收效果的三个关键参数中，α决定CPML的优势吸收频率，σ和κ影响CPML的吸收效率.但是，κ>1会使CPML中出现不可避免的数值色散，κ越大、θ越小则数值色散越严重，CPML的数值色散主要发生在外层，如不能很好的压制，外层电磁场会出现持久的高频震荡并影响到内部正演区域.

(2) 异常体的垂直磁场分量Hzd和Hzd的第一极值时刻T1可以作为评价优势探测区域的标准.正演实验结果显示，仅仅是异常体电导率的变化不会引起T1的变化，同一位置处Hzd(T1)比上Hzd(T2)为定值；Hzd的优势探测区域是以收发线圈的连线为长轴的椭球体内侧区域，越靠近收发线圈Hzd的幅值越大，高阻异常体对应的内侧区域为极大值，外侧区域为极小值；T1的优势探测区域则是以收发线圈的连线为长轴的椭球体外侧区域，越靠近收发线圈连线的中点T1的值越小.

针对以上结论，提出CPML与井间电磁勘探中的建议如下：

(1) 为了兼顾低频电磁波的吸收和高频数值色散的压制，CPML的最优参数设置模式为：首先选择起止时刻波形平滑的激励源；然后根据激励源的频谱范围来计算α，αmin>αmax能有效吸收数值色散带来的高频电磁波；根据激励源主频的大小来确定κmax和δmax，当激励源主频较高时令κmax取较小值，当激励源主频较低时令κmax取较大值；再根据背景场电导率选择合适的σmax；最后参考正演结果反馈调整CPML的参数.

(2) 能有效提高井间电磁正反演信噪比的方法有：加密收发线圈及异常体附近的网格；增加阵列感应测井或电阻率测井以获得泥浆侵入剖面；增加声电成像测井或地层倾角测井以获取地层剖面信息.

(3) 井间电磁勘探中最好的取井方案是采用三口(及以上)不在同一直线上的井做两组(及以上)观测，实际生产中也可以选择两口不平行的井段，以减小异常体位置的多解性.

References

Al-Ali Z A, Al-Buali M H, AlRuwaili S, et al. 2009. Looking deep into the reservoir.OilfieldReview, 21(2): 38-47.

Alumbaugh D L, Morrison H F. 1995. Theoretical and practical considerations for crosswell electromagnetic tomography assuming a cylindrical geometry.Geophysics, 60(3): 846-870. Bérenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves.JournalofComputationalPhysics, 114(2): 185-200. Bérenger J P. 1996. Perfectly matched layer for the FDTD solution of wave-structure interaction problems.IEEETransactionsonAntennasandPropagation, 44(1): 110-117. Bérenger J P. 2007. Perfectly Matched Layer (PML) for Computational Electromagnetics. Arizona: Morgan & Claypool. Bérenger J P. 2012. An optimized CFS-PML for wave-structure interaction problems.IEEETransactionsonElectromagneticCompatibility, 54(2): 351-358.Carcione J M, Gei D, Picotti S, et al. 2012. Cross-hole electromagnetic and seismic modeling for CO2detection and monitoring in a saline aquifer.JournalofPetroleumScienceandEngineering, 100: 162-172.

Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified Maxwell′s equations with stretched coordinates.MicrowaveandOpticalTechnologyLetters, 7(13): 559-604. de la Kethulle de Ryhove S, Mittet R. 2014. 3D marine magnetotelluric modeling and inversion with the finite-difference time-domain method.Geophysics, 79(6): E269-E286.Donadille J M, Al-Ofi S M. 2012. Crosswell electromagnetic response in a fractured medium.Geophysics, 77(3): D53-D61.

Elsherbeni A, Demir V. 2009. The Finite-Difference Time-Domain Method for Electromagnetics with MATLAB Simulations. Raleigh: SciTech Publishing.

Kuzuoglu M, Mirrta R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers.IEEEMicrowaveandGuidedWaveLetters, 6(12): 447-449.

Li Z H, Huang Q H. 2014. Application of the complex frequency shifted perfectly matched layer absorbing boundary conditions in

transient electromagnetic method modeling.ChineseJ.Geophys. (in Chinese), 57(4): 1292-1299, doi: 10.6038/cjg20140426.Maclennan K, Karaoulis M, Revil A. 2014. Complex conductivity tomography using low-frequency crosswell electromagnetic data.Geophysics, 79(1): E23-E38. Newman G. 1995. Crosswell electromagnetic inversion using integral and differential equations.Geophysics, 60(3): 899-911.Roden J A, Gedney S D. 2000. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media.MicrowaveandOpticalTechnologyLetters, 27(5): 334-339.

Shen J S, Wang Z G, Ma C, et al. 2014. Application of the cross-hole electromagnetic method (CHEM) in hydrocarbon reservoir monitoring.OilGeophysicalProspecting(in Chinese), 49(1): 213-224.

Wei B J, Chen T, Hou X L, et al. 2014. Simulating cross-hole electromagnetic field′s response with metal casing using Green′s functions of radial-layered medium and integral equations.JournalofChinaUniversityofPetroleum(in Chinese), 38(1): 57-63.

Wilt M J, Alumbaugh D L, Morrison H F, et al. 1995. Crosswell electromagnetic tomography: System design considerations and field results.Geophysics, 60(3): 871-885.

Zeng W C, Zhao W J, Zang D F. 2001. Application research of crosshole electromagnetic tomography.ChineseJ.Geophys. (in Chinese), 44(3): 411-420.

Zhang G J. 1982. High order geometrical factors of induction logging.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 25(4): 370-378.

附中文参考文献

李展辉, 黄清华. 2014. 复频率参数完全匹配层吸收边界在瞬变电磁法正演中的应用. 地球物理学报, 57(4): 1292-1299, doi: 10.6038/cjg20140426.

沈金松, 王志刚, 马超等. 2014. 井间电磁油气储层监测技术的发展和应用. 石油地球物理勘探, 49(1): 213-224.

魏宝君, 陈涛, 侯学理等. 2014. 利用径向成层介质的Green函数和积分方程模拟含金属套管井间电磁场的响应. 中国石油大学学报(自然科学版), 38(1): 57-63.

曾文冲, 赵文杰, 臧德福. 2001. 井间电磁成像系统应用研究. 地球物理学报, 44(3): 411-420.

张庚骥. 1982. 感应测井的高次几何因子. 地球物理学报, 25(4): 370-378.

(本文编辑何燕)

Three-dimensional cross-well electromagnetic modeling considering numerical dispersion in convolutional perfectly matched layers

FANG Si-Nan1, PAN He-Ping1*, DU Ting2, WANG Zhi1, DENG Cheng-Xiang1

1InstituteofGeophysicsandGeomatics,ChinaUniversityofGeosciences,Wuhan430074,China2HubeiCoalGeologicalSurveyInstitution,ChinaNationalAdministrationofCoalGeology,Wuhan430070,China

AbstractTaking Convolutional Perfectly Matched Layers (CPML) as the absorbing boundary conditions, this paper applied Finite-Difference Time-Domain (FDTD) into 3D modeling of cross-well electromagnetic (CWEM). The study proved that it was the real stretch which induced numerical dispersion in CPML, given the anisotropy effect of phase velocity of electromagnetic wave from the conventional real stretch and grid interval, and verified numerical dispersion in CPML through wave field snapshot; further on, generalized the restriction between the dominant frequency of source and maximum of real stretch, maximum of grid interval in CPML, so as to improve optimal parameter settings in CPML. Based on optimal CPML, we utilized the vertical magnetic field and the traveling time of second field to describe the distribution of sensitivity, so as to designate the dominant area of cross-well electromagnetic prospecting, and proposed the logging suite for restraint and preferred plan for selecting well which were required in the process of the modeling and inversion of cross-well electromagnetic.

KeywordsCross-Well Electromagnetic (CWEM); 3D modeling; Finite-Difference Time-Domain (FDTD); Convolutional Perfectly Matched Layers (CPML); Numerical dispersion

基金项目国家自然科学基金项目(41074086)资助．

作者简介方思南，男，1987年生，博士研究生，主要从事测井处理解释和井间电磁正反演方面的研究. E-mail: fangsinan@163.com *通讯作者潘和平，男，1953年生，教授，博士生导师，主要从事测井与井中物探的教学和科研工作.E-mail: panpinge@163.com

doi:10.6038/cjg20160531 中图分类号P631

收稿日期2015-02-02，2016-04-06收修定稿

方思南， 潘和平， 杜婷等. 2016. 考虑卷积完全匹配层数值色散的井间电磁三维正演.地球物理学报，59(5):1888-1897,doi:10.6038/cjg20160531.

Fang S N, Pan H P, Du T, et al. 2016. Three-dimensional cross-well electromagnetic modeling considering numerical dispersion in convolutional perfectly matched layers.ChineseJ.Geophys. (in Chinese),59(5):1888-1897,doi:10.6038/cjg20160531.