基于对数目标函数的跨孔雷达频域波形反演

孟旭， 刘四新， 傅磊， 王宪楠， 刘新彤， 王文天， 蔡佳琪

吉林大学地球探测科学与技术学院， 长春　130026

基于对数目标函数的跨孔雷达频域波形反演

孟旭， 刘四新*， 傅磊， 王宪楠， 刘新彤， 王文天， 蔡佳琪

吉林大学地球探测科学与技术学院， 长春130026

摘要波形反演在探地雷达领域的应用已有十余年历史，但绝大部分算例属于时间域波形反演.频率域波形反演由于能够灵活地选择迭代频率并可以使用不同类型的目标函数，因而更加多样化.本文的频率域波形反演基于时间域有限差分(FDTD)法，采用对数目标函数，可在每一次迭代过程中同时或者单独反演介电常数和电导率.文中详细推导了频率域波形反演的理论公式，给出对数目标函数下的梯度表达式，并使用离散傅氏变换(DFT)实现数据的时频变换，能够有效地减少大模型反演的内存需求.在后向残场源的时频域转换过程中，提出仅使用以当前频点为中心的一个窄带数据，可以消除高频无用信号的干扰，获得可靠的反演结果.为加速收敛，采用每迭代十次则反演频率跳跃一定频带宽度的反演策略.实验证明适当的频率跳跃能够在不降低分辨率的基础上有效地提高反演效率.通过两组不同情形下合成数据反演的分析对比，证明基于对数目标函数的波形反演结果准确可靠.最后，将该方法应用到一组实际数据，得到较好的反演结果.

关键词波形反演； 对数目标函数； 介电常数； 电导率； 钻孔雷达

In this paper, waveform inversion is implemented by means of a finite-difference time-domain solution of Maxwell′s equations and a logarithmic objective function is applied. Permittivity and conductivity can be updated simultaneously or separately at each iterative step. The derivation process of the formulas is described in detail and we show the specific expression of gradient under the logarithmic objective function. It is important to note that the gradient formula of the frequency domain waveform inversion is different from the gradient formula of the time domain waveform inversion. The reason is that the cost function is essentially different. Discrete Fourier transform (DFT) is applied to transform time domain data into the frequency domain, which only increases a few calculations in the inversion. The method can greatly reduce memory requirement when the inverted model is on a large scale. When transforming the back-residual source, we present that only a narrow-band data whose center is the current frequency is used. The method can effectively reduce the interference of high frequency information, so reliable inversion results can be obtained.

In order to accelerate the convergence, a special frequency strategy is applied. The inversion frequency skips a number of bandwidth after every ten times iterative step. Results turn out that the strategy can efficiently improve the inversion efficiency and does not influence the resolution. To verify the effect of our algorithm, we test it on two different synthetic data. Then we compare with the results of conventional waveform inversion: (1) Two small cylindrical bodies of permittivity in a layered medium. (2) A layered medium with multiple embedded cylindrical inclusions of permittivity and conductivity. Finally, we apply the logarithmic algorithm to field data.

The results on synthetic data show that the logarithmic waveform inversion is better than the conventional waveform inversion. When permittivity and conductivity are inverted at the same time, the results of logarithmic waveform inversion can accurately reconstruct both shape and location of the inclusions. This is because that the amplitude of the residual is normalized by the amplitude of the modeled wavefield. The inversion results of the field data also prove the practical value of logarithmic waveform inversion.

1引言

探地雷达层析成像在地质学、工程学和水文地质学中应用广泛(Pettinelli et al.,2009; Liu and Sato, 2002; Liu et al., 2011,2014；傅磊等，2014)，但传统的层析成像技术(比如走时成像和衰减成像)由于只能利用一部分的信号信息，所提供的结果分辨率有限(Williamson and Worthington,1993).波形反演技术能够提供亚波长级分辨率的地下介质分布图像，因此在近些年深受瞩目.Kuroda等(2005)使用全波形反演的方法对跨孔雷达数据成像，但只考虑介电常数.Ernst等(2007a)的波形反演方法能够通过级联的方式既考虑介电常数又考虑电导率.Meles等(2010)提出了矢量全波形反演技术，实现了介电常数和电导率的同步迭代.在实际数据处理方面，Cai等(1996)使用程函方程对实际数据进行反演；Zhou等(2007)的时间域重建法属于波形反演方法，使用实际数据反演了介电常数和电导率；Ernst等(2007b)将全波形反演应用到跨孔雷达实际数据处理中，对源子波估计和实际数据的三维校正等问题作了一定分析.国内方面，王兆磊等(2007)使用雷达数据反演了地下介质的物性参数；周辉等(2014)提出了一种不需要提取激发脉冲的探地雷达波形反演方法.

目前探地雷达波形反演方法大部分属于时间域波形反演，但在地震波形反演中，频率域波形反演占据重要地位.自从Pratt等(1998)将后向传播技术应用在大尺度地质模型的频率域波形反演后，该技术被广泛使用在频率域地震波形反演中.相对于时间域波形反演，频率域波形反演具有多变的频率选择策略并能够选择多种目标函数.Song等(1995)的串行反演策略是将低频数据波形反演结果作为相邻高频数据波形反演结果的初始模型，该方法因具有较高的稳定性被广泛应用于波形反演中.Pratt(1999), Pratt和Shipp (1999)将有效频段内的频率域数据按从低频到高频分组，较低频组的反演结果作为相邻较高频组的初始模型，该策略为组间串行反演策略，有利于压制噪声和反演假象.Sirgue和Pratt(2004)对近层状模型反射地震数据多频反演的频率间隔选择策略做了研究.目标函数方面，即使在地震波形反演中，很长一段时间内反演目标函数一直在使用理论波场与观测波场残差的l2范数(Tarantola, 1984，1986; Pratt, 1990; Pratt and Worthington,1990; Pratt et al., 1998).Shin和Min(2006)提出了基于自然对数波场的反演目标函数，即对数目标函数，并取得了较好的效果.Chung等(2007)使用混合l1/l2范数的Huber函数作为频率域波形反演的目标函数.

本文在Maxwell方程的频率域表达式基础上，详细推导了基于对数目标函数的频率域波形反演理论公式，并指出其梯度公式与时间域波形反演梯度公式之间不是简单对应关系.尽管这两者在表达式上是对应的，但不能仅通过对公式的时频转换得到.反演中的正演过程使用时间域有限差分(FDTD)法，之后利用离散傅里叶变换(DFT)将时间域数据转换为频率域数据，并在频率域计算梯度.相对于时间域波形反演，使用DFT技术不需要保存所有时间步长的电场值，能够极大地减少大尺度模型反演过程中的计算机内存需求.在计算后向传播场时，残场源是在频率域计算的，因此需要将残场源转换到时间域.为了避免高频无用信号的干扰，我们提出在残场源的时频域转换过程中，只使用以当前反演频率为中心的一个窄带内频域数据，有利于提高稳定性.文中反演频率的选择采用串行反演策略，为了加速收敛，每迭代若干次后将反演频率增加10 MHz.由于在跨孔模式下每组发射天线对应的接收数据是相互独立的，我们采用MATLAB分布式计算引擎(Matlab Distributed Computing Engine，MDCE)，通过建立一个局域网机群，实现正演的并行运算，能够明显地提高反演效率.

通过两组合成数据来检验本文波形反演方法的效果.第一组合成数据只反演介电常数，用来验证文中提出的反演策略；第二组模型同时反演介电常数和电导率，结果证明基于对数目标函数的频率域波形反演比基于传统目标函数的频率域波形反演更加准确.在实际数据处理方面，仍需要考虑数据的三维校正和源子波估计等问题，在此基础上给出了实际数据的反演结果.

2理论

2.1正演问题的频域表达形式

在探地雷达地球物理问题中，使用介电常数和电导率来描述地下介质的分布情况，并假设磁导率是均匀不变.Maxwell方程可以表示为如下矩阵形式：

(1)

(2)

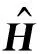
(3)

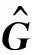
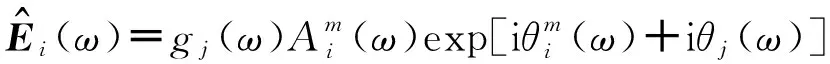
(4)

2.2对数目标函数及梯度计算

不同于Shin和Min(2006)通过对目标函数和声波方程求导来推导梯度的办法，本文的理论推导基于Meles等(2010)的波形反演理论(吴俊军等，2014)与对数目标函数的联合.(5)式为频率域波形反演中使用最广泛的传统目标函数，它是正演模拟数据与实际数据差的l2范数：

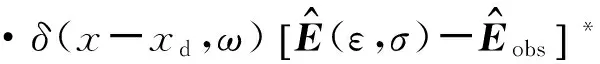
(5)

本文使用的目标函数为基于自然对数的正演模拟数据与实际数据差的l2范数：

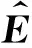
(7)

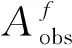
+iθj(ω)+2πnj],

(8)

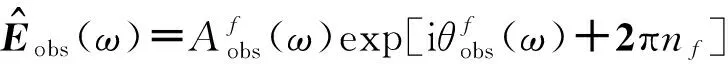
(9)

nm，nj和nf为计算得到的整数值.则

(10)

正如(10)式中表明的，需要对相位进行反缠绕来获得有意义的相位信息，但这个过程通常难以实现.假定nm+nj=nf.该假定隐含了正演模型必须与真实模型接近这个条件，从而反缠绕过后的实际数据的相位与正演数据的相位具有相同的度数(ShinandMin，2006).则目标函数写成：

(11)

从(11)式发现，目标函数为相位误差及对数振幅误差的l2范数形式，这也是对数目标函数的特点，能够实现振幅和相位的自然分离.全波形反演层析成像的目的是寻找目标函数S(ε,σ)最小时对应的介电常数ε和电导率σ空间分布.本文使用最速下降法来寻找目标函数最小.为了得到目标函数的梯度，写出扰动系统下的Maxwell方程组：

(12)

(12)式减去(1)式得：

(13)

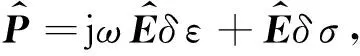
(14)

在空间域，这是一个关于扰动正演电场的方程.将(14)式代入(3)式中：

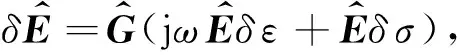
(15)

(16)

(17)

则

(18)

目标函数梯度的推导使用扰动目标函数的一阶近似：

+O(δ ε2,δ σ2),

(19)

扰动目标函数为：

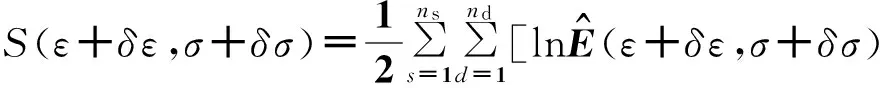
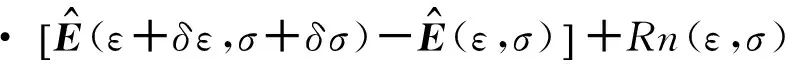
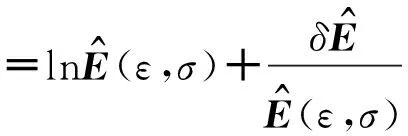
(21)

其中，Rn(ε,σ)代表高阶项.将(21)式代入(20)式中展开化简得到：

(22)

(23)其中

(24)

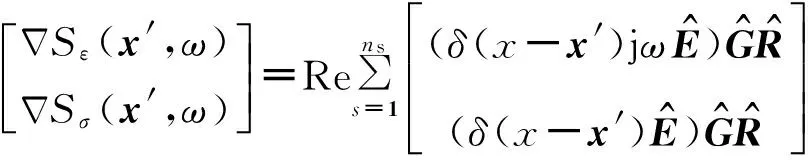
(25)

(26)

(25)式为最终的梯度表达式.需要注意的是，梯度公式中的Re表示取复数的实部.这是因为在推导梯度过程中，(22)式与梯度相关的项在简化时虚部互相抵消了.尽管推导的方式不同，式(25)与频率域地震波形反演表达类似，但如果仅根据时间域波形反演的梯度公式做傅里叶变换得到频率域的梯度公式，其表达是不正确的.本文(23)式的推导过程中做了一些省略，具体情形参考Meles等(2010)及吴俊军等(2014)的论文.

2.3后向传播残场源

由于残场源首先在频率域计算，之后经傅里叶变换至时间域作为后向传播FDTD中的源项.与基于传统目标函数的频率域波形反演不同，不能直接使用正演数据和实际数据的频域场值来计算后向残场源，这是因为(24)式中包含的除法会在计算过程放大原来无用的高频噪声.本文的正演在时间域进行，反演在频率域进行，因此后向传播过程中需要经历二次傅里叶变换和一次反傅里叶变换(后向残场源的正反变换和整个模型空间电场值的正变换).

图1a显示了一道实际数据及与它对应的正演数据的时间域波形，图1b为两者的频谱.从图1b中可以看出，信号的有效频率范围大致在250 MHz以下，也就是说高于250 MHz的信息为无用的噪声.使用图1a中的正演波形和实际波形对应的全部频域数据，经(24)式计算并做反傅里叶变换，得到图1c中后向残场源的时间域波形.图1d中实线为图1c对应的频谱，虚线为(24)式直接计算的结果.对比发现使用所有频域数据的结果完全丧失了本应具备(直接计算结果)的特征，这是因为(24)式包含的除法，放大了250 MHz之后的噪声信息.这些无意义的噪声在频谱中占据了主导地位，经过反傅里叶变换得到图1c中的无效波形.图1f为本文使用的有限点频谱转换方法：选择以当前反演频率为中心的，带宽在20 MHz左右范围内的频率数据，且指定其他频率数据极小(10-8+10-8j).之后反傅里叶变换得到时间域的后向残场源.图1e为以80 MHz为中心的后向残场源.图1f中实线为使用频率域数据直接计算的频域后向残场源；点虚线、短虚线和长虚线分别为以80 MHz，130 MHz和180 MHz为中心计算的时间域后向残场源的频谱.从图1f中可以看出，我们的方法能够有效保证后向传播残场源在对应频率范围内的正确性.

图1为了显示方便，我们最多给出了300 MHz内的频谱.需要注意的是：图1b中300 MHz之后的频域数据极小；图1d和图1f中直接计算得到的残场源频谱随着频率的增加急剧增大，之后的频域数值比我们关注的300 MHz以内的频域数值高出好几个数量级(对比图1d中虚线和图1f中实线，两者为显示范围不同下的同一数据)，这使得传统带通滤波方法压制高频噪声的效率很低.因此本文提出利用有限频点来计算后向残场源，之后的合成数据以及实际数据结果也证明了该方法的有效性.

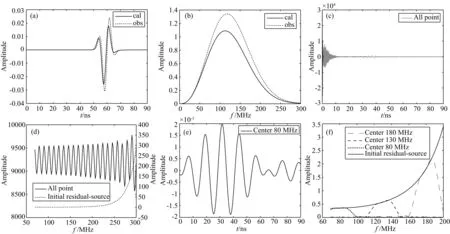
图1　后向传播残场源的变换(a)实线为正演数据，虚线为实际数据； (b) 实线为正演数据的频谱，虚线为实际数据的频谱； (c) 使用所有频点计算得到的后向残场源； (d) 实线为(c)对应的频谱，虚线为直接由式(24)计算的频谱.左侧y轴对应实线振幅，右侧y轴为虚线振幅； (e) 以80 MHz为中心的窄带数据计算的时间域后向残场源； (f) 中心频率为80 MHz、130 MHz、180 MHz及直接使用公式(24)计算的后向残场源频谱.Fig.1　Transformation of the back-residual source(a) Solid line shows model data, and dashed line shows field data; (b) Frequency spectrum of (a); (c) Time domain back-residual source computed using all frequency points; (d) Solid line is frequency spectrum of (c), and dashed line is frequency spectrum directly computed from formula (24). Left ‘y’ axis corresponds to amplitude of solid line and right ‘y’ axis corresponds to amplitude of dashed line; (e) Time domain back-residual source under the center frequency of 80 MHz; (f) Frequency spectrum of back-residual source under the center frequency of 80 MHz, 130 MHz, 180 MHz and by using formula (24), respectively.

2.4迭代步长的求解

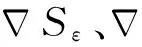
(27)

(28)

(29)

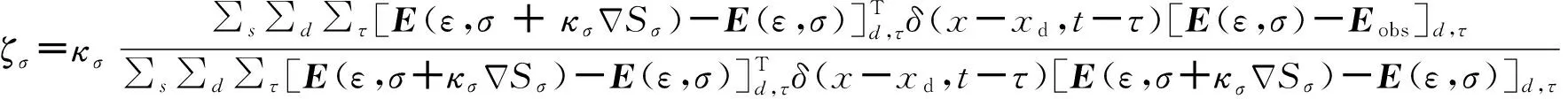
(30)

这里需要注意的是，κε、κσ为不同的小稳定因子，必须小心地为其选择适当的值并且在反演过程中随着迭代更新.

在本文的频率域波形反演中，正演使用时间域有限差分(FDTD，O(2,4)).梯度的计算是在频率域完成的，也就是说每次正演之后都需要将时间域的电场值转换到频率域.我们使用离散傅里叶变换(DFT)来进行时频转换，这样无需保存所有时间的场值(能够极大地减少内存需求)，仅需在FDTD的每一次时间迭代中计算一次然后叠加即可：

(31)

整个反演过程如图2所示，正演都在时间域进行，而梯度及残场源的计算在频率域进行.需要注意的是，后向传播场的残场源，是在频率域计算后经反傅里叶变换得到的.在本文中，为了避免高频无用信号的干扰，提出只使用以当前反演频率为中心的一个窄频带内的数据进行时频转换.在计算完梯度，迭代步长是在时间域计算的，之后对模型更新直至收敛完成.整个波形反演中各个步骤之间的计算顺序是按照图2自上而下进行的.

图2　频率域波形反演流程图虚线代表数据的时频域转换，黑线代表波形反演流程.Fig.2　Flow chart of frequency domain waveform inversionDashed lines stand for Fourier transform and black lines represent waveform inversion process.

3算例

3.1复杂目标体介电常数成像及频率选择策略

为了验证文中频率域对数波形反演层析成像的能力，建立如图3a所示的复杂模型.模型大小为6 m×6 m，包含3个地层：其中第1层与第3层地层参数相同，相对介电常数都为5；中间层的相对介电常数为5.5，并埋藏有两根异常体管线；异常体位于深度3 m处，间隔1 m，相对介电常数为7；认定所有地层与异常体的电导率相同且已知，均为0.001 S·m-1.在本次模拟中共13组发射(圆圈表示)，每组发射对应13组接收(叉号表示).发射器与接收器位置均为垂直方向0 m到6 m之间，并以0.5 m等间隔排列.在本次反演中，我们认为电导率是已知的，只对介电常数成像.初始的介电常数模型采用均匀地层，相对介电常数值为5.5，与中间层相同.

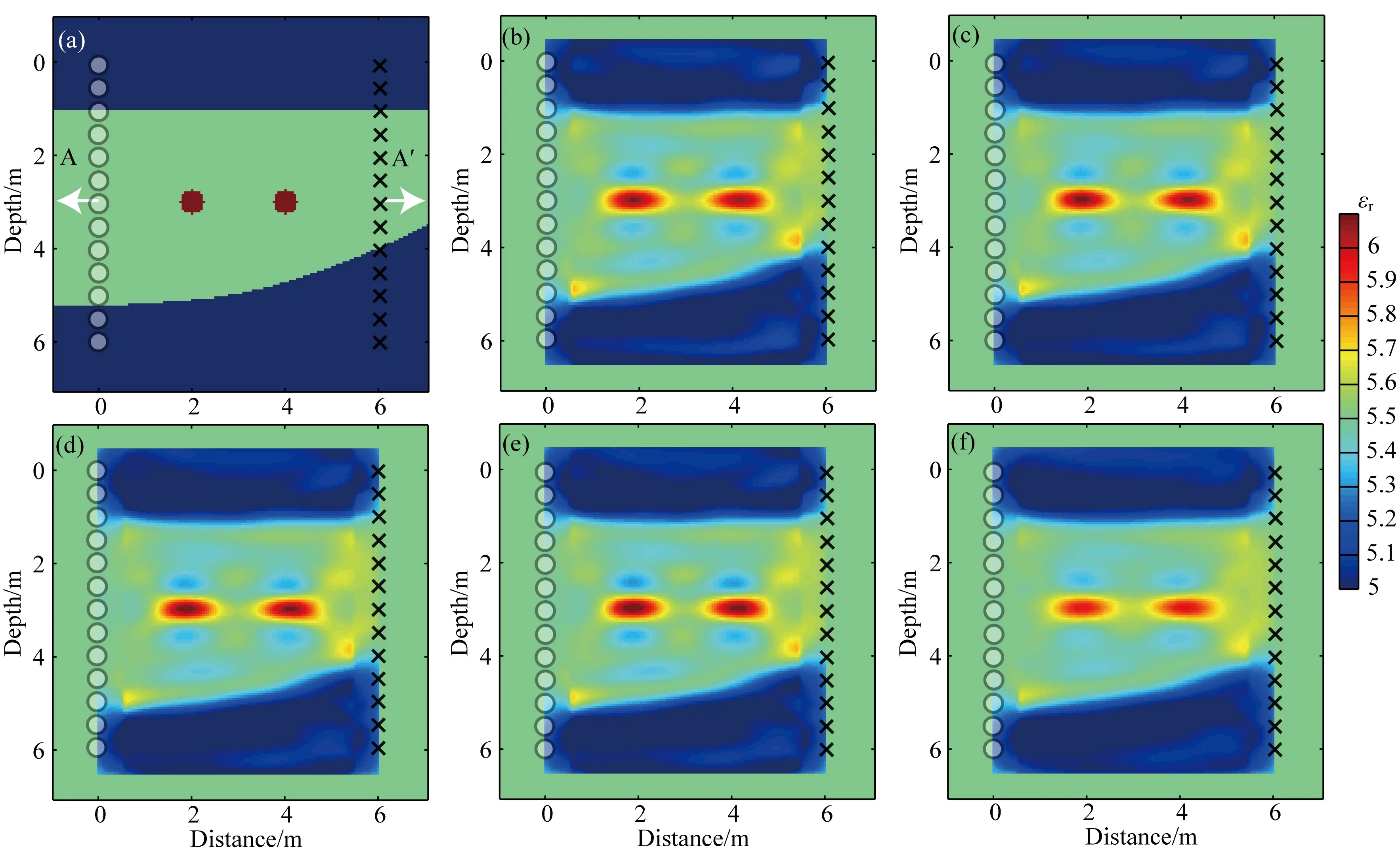
图3　不同频率策略下的相对介电常数反演结果(a) 真实模型； (b) fS=0 MHz； (c) fS=10 MHz； (d) fS=20 MHz； (e) fS=30 MHz； (f) fS=40 MHz.Fig.3　Relative permittivity results of different frequency strategies(a) Real model; (b) fS=0 MHz; (c) fS=10 MHz; (d) fS=20 MHz; (e) fS=30 MHz; (f) fS=40 MHz.

反演的起始频率为50 MHz，每经过一次反演则反演频率增加2 MHz.为了加速收敛，每十次反演之后，反演频率进行一次跳跃.例如：当前反演次数为n，则反演频率为50+fS·int(n/10)+2(n-1) MHz，其中int表示取正整数，fS为跳跃的频率宽度.为了验证该频率策略，以图3a为真实模型进行反演：图3b为无频率跳跃时的对数波形反演结果；图3c、3d、3e、3f分别为频率跳跃宽度为10 MHz、20 MHz、30 MHz、40 MHz时的对数波形反演结果.为了使不同结果之间更具对比性，在每个频点处只反演一次，且最终的反演频率都为228 MHz.

从结果来看，5种不同模式下的对数波形反演结果都能清晰地重建上下两层界面及中间层中埋藏的异常体管线，但图3f中两个异常体管线的成像效果较弱.图4a为5种模式波形反演对应的目标函数曲线：青绿色曲线为无频率跳跃时的目标函数曲线，红色、绿色、蓝色和洋红色曲线分别对应跳跃频率宽度为10 MHz、20 MHz、30 MHz和40 MHz时的目标函数曲线.由于前10次反演的频率完全相同，故在图4a中所有曲线在10次之前重合.无频率跳跃的曲线收敛较慢，这是由于该模式下低频部分的反演次数较多造成的.图4a同时也反映了不同模式的反演效率：无频率跳跃模式下共反演90次，频率跳跃宽度为10 MHz时共反演60次，随着频率跳跃宽度的增加反演次数分别为50、45和30.图4b为沿AA′方向的介电常数切线，黑线为真实模型，可以看出只有当频率跳跃宽度为40 MHz时反演效果出现明显的降低，而其他结果无较大差别.

图3证明在频率域波形反演中，适当的频率跳跃能够有效地加速反演过程的收敛且不影响效果.需要注意的是：随着频率跳跃宽度的增大，计算效率的提升是递减的；如果频率跳跃宽度过大，则反演频率的不足会影响反演结果(图3f).因此，要在计算效率和反演效果之间取舍，选择恰当的频率跳跃宽度.另外，频率跳跃的可行性建立在第一次频率跳跃之前反演过程已经取得较好收敛效果的基础上.这隐含了一个条件，即：在频率跳跃之前，目标函数已经收敛到全局最小附近.在本文之后的算例中，选择较为保守的10 MHz为频率跳跃宽度.

3.2介电常数和电导率同时成像

以上算例证明了基于对数目标函数的频率域波形反演在单介电常数成像(认定电导率均匀且已知)的能力和文中反演策略的有效性.在实际情况中，介电常数和电导率是同时变化的，本例对介电常数和电导率同时反演并与基于传统目标函数的频率域波形反演结果对比.

真实模型如图5a和图5d所示，发射天线(用圆圈表示)位于水平距离0 m，深度从0 m到20 m，共41个发射，间距0.5 m；接收天线(用叉号表示)位于水平距离10 m处，深度同样从0 m到20 m，间距0.5 m共41个.三根直径为0.5 m的管线异常体位于深度6.5 m处，互相之间间隔2 m，相对介电常数为7，电导率为0.008 S·m-1.另一个较大的管线异常体位于深度12 m，直径为1 m，相对介电常数为6.5，电导率为0.005 S·m-1.整个模型分为三层，所有的异常体都埋藏在中间层，顶层和底层的电性参数相同(吴俊军等，2014).将反演的起始频率定在30 MHz，采用与之前算例相同的频率策略.图5b、5e、5c、5f为迭代60次之后的反演结果.

图5c和图5f分别为对数目标函数下介电常数和电导率反演结果，图5b和图5e分别为传统目标函数下介电常数和电导率结果.能够很明显地看出对数目标函数的结果优于传统目标函数的结果：深度6.5 m处的三根管线异常体，在图5c和图5f中表现得十分清晰，且互相之间分隔很好；而图5b和图5e中异常连到一起，无法辨认出异常体的数量和形状.对于深度12 m处的大异常体，传统目标函数的结果表现出明显的畸变(水平方向拉长)，而对数目标函数的结果与真实模型十分接近，表现为正圆而非椭圆.

图6a为沿AA′方向的介电常数切线，图6b为沿BB′方向的电导率切线.对比真实模型、对数目标函数结果和传统目标函数结果在相同位置切线的形态和数值，对数目标函数结果更接近真实模型，也更能表现出异常体的形态.从图6b发现，对数目标函数结果与真实模型在数值上的一致性相当好，这说明了在同时反演的情况下，电导率成像效果好于介电常数成像(吴俊军等，2014).在传统的射线理论反演中，介电常数反演要比电导率反演容易，这是因为走时成像在理论上比衰减成像完善.而在波形反演中，电导率成像效果好于介电常数成像效果是由于波形中振幅信息对电导率的变化更加敏感(相对于相位信息对介电常数的变化).

图7为第21个源(Depth：10 m)发射，60次迭代后的模型的模拟接收波形与实际数据波形的对比(接收器波形为41道，为显示方便，每隔四道选择一道).尽管图5中传统目标函数波形反演成像结果与真实模型差别较大，但在图7a中，蓝线代表的反演数据波形与实际数据波形仍符合很好，这说明传统目标函数波形反演结果是收敛的.图7c中的蓝线和红线分别为图7a中的蓝线与黑线的差和图7b中红线与黑线的差.在图7c第25道至41道，能够明显发现蓝线有异常，说明图7a中传统目标函数结果与真实模型之间的差要大于图7b中对数目标函数结果与真实模型的差.这也证明了对数目标函数波形反演优于传统目标函数波形反演.

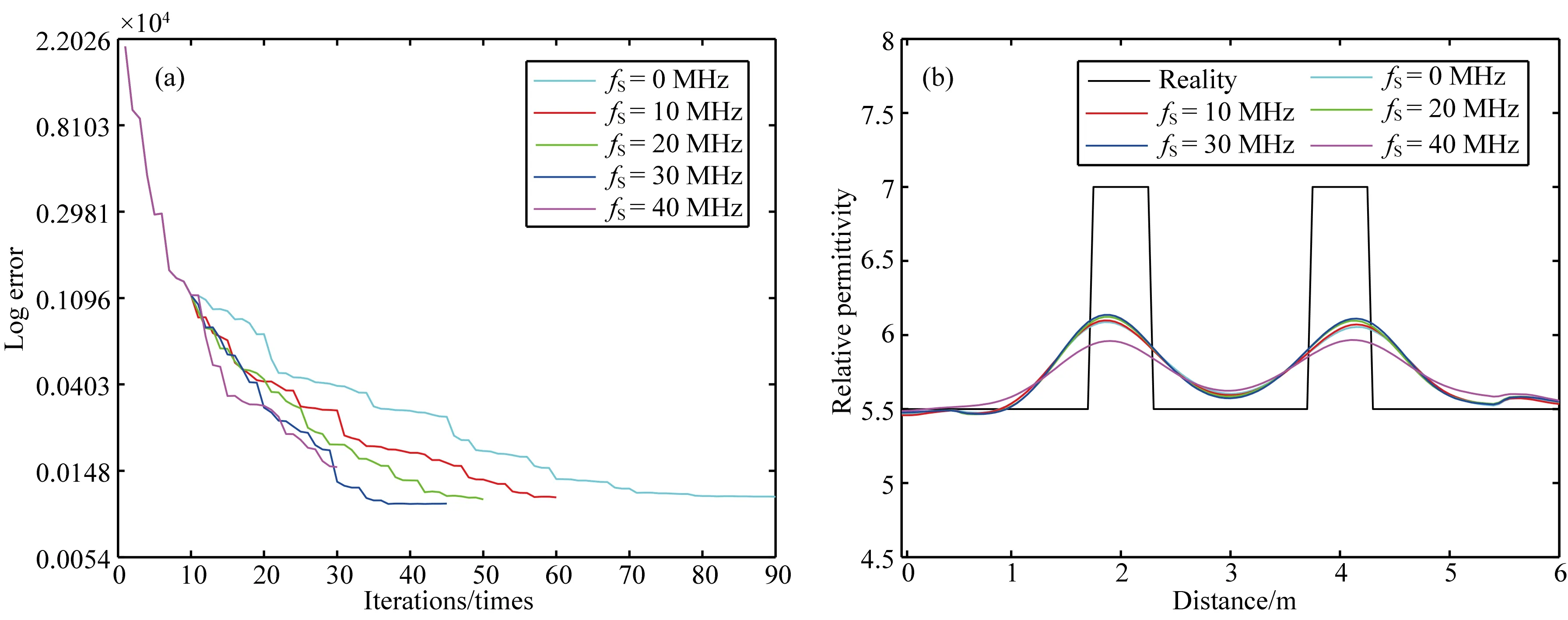
图4　(a)目标函数收敛曲线； (b) 深度3 m介电常数切线(沿AA′方向)Fig.4　(a) Objective function convergence curves; (b) Permittivity in the depth of 3 m (along AA′ line)

图5　介电常数和电导率同时成像(a)介电常数真实模型； (b) 传统目标函数下介电常数反演结果； (c) 对数目标函数下介电常数反演结果； (d) 电导率真实模型； (e) 传统目标函数下电导率反演结果； (f) 对数目标函数下电导率反演结果.Fig.5　Simultaneous tomography of permittivity and conductivity(a) Real model of permittivity; (b) Permittivity results of conventional object function; (c) Permittivity results of logarithmic object function; (d) Real model of conductivity; (e) Conductivity results of conventional object function; (f) Conductivity results of logarithmic object function.

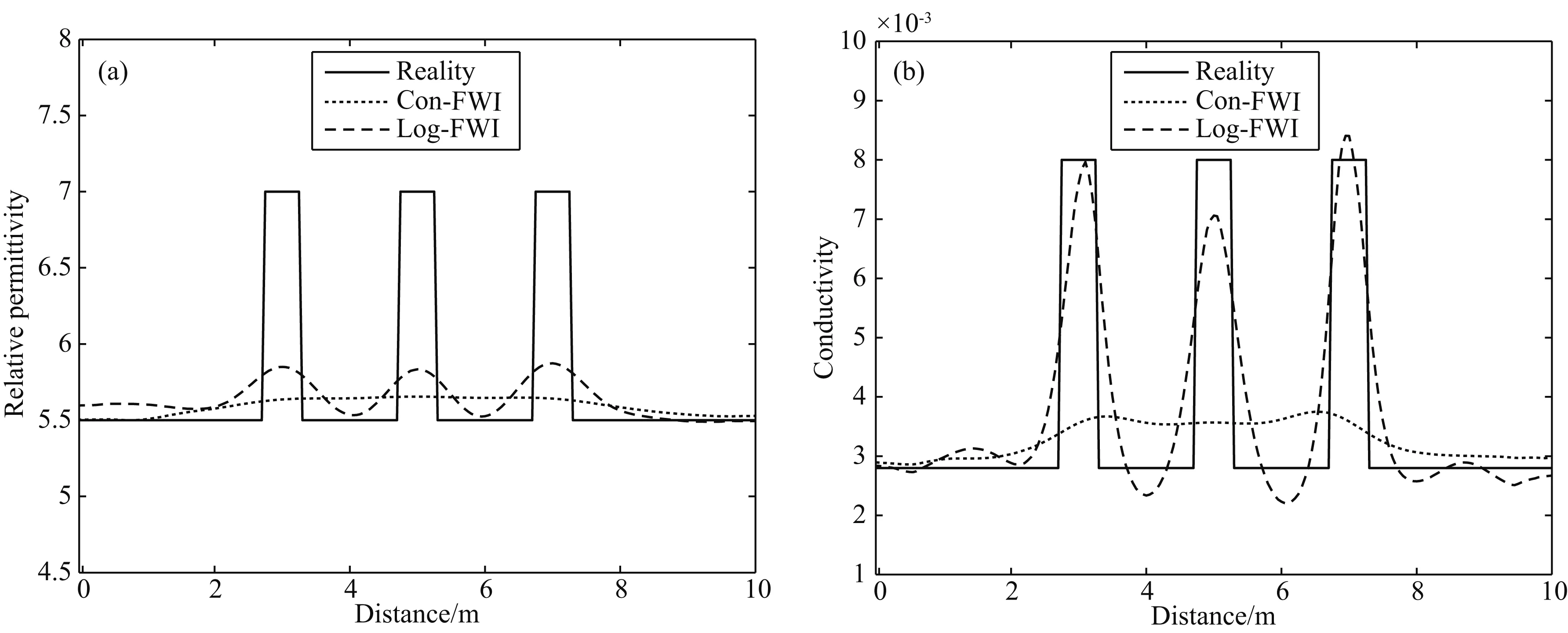
图6　(a) 介电常数AA′切线； (b) 电导率BB′切线Fig.6　(a) Permittivity along AA′ line; (b) Conductivity along BB′ line

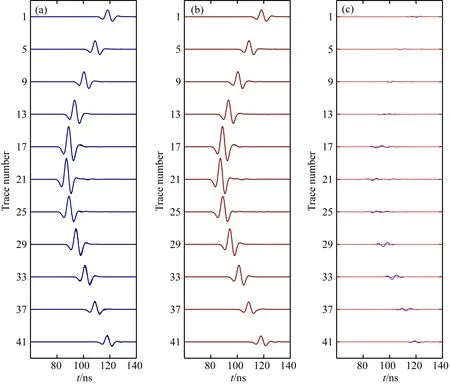
图7　第21个源(depth：10 m)发射，接收器接收到的波形对比(a)60次迭代后传统目标函数波形反演数据(蓝线)与实际数据(黑线)对比； (b) 60次迭代后对数目标函数波形反演数据(红线)与实际数据(黑线)对比； (c) 蓝线为(a)中蓝线与黑线的差，红线为(b)中红线与黑线的差.Fig.7　Transmitter gathers generated by the source placed at a 10 m depth in Fig.5(a) Blue and black lines express the differences of radar trace generated from the results of conventional waveform inversion and field data after 60 iterations; (b) Red and black lines show the differences of radar trace generated from the results of logarithmic waveform inversion and field data after 60 iterations; (c) Blue line represents the difference between blue and black lines in (a), red line shows the difference of red and black lines in (b).

3.3实际数据

数据采集地位于中国西南的贵州省，地貌属于西南部高原山地，并且境内喀斯特地貌发育丰富，岩溶分布范围广泛.采集过程使用中心频率为100 MHz的MALA钻孔雷达系统，探测的两个钻孔之间的水平距离为18 m.反演中使用的数据包含40组发射，其中发射源以1 m等间隔分布在9 m至48 m深度范围内.接收器的总覆盖范围为0 m至47 m，但每个源对应的接收器范围和数目都不相同.由于缺乏对应地质资料，无法获得钻孔所在地详细的地质信息.初始模型分别由走时成像(王飞等，2013)和重心频率下降法(Liu et al., 1998)得到.

在对实际数据进行波形反演之前，首先对实际数据进行了一系列的预处理，包括提取数据、滤波等.之后，采用Ernst等(2007b)的办法对实际数据做三维校正，另外在实际数据的波形反演过程中，共进行了三次源子波估计.

图8a和图8c分别为基于走时反演结果计算的相对介电常数和重心频率下降法得到的电导率分布图像，图8b和图8d为对数目标函数波形反演得到的相应结果.图9给出了第10个源(Depth：19 m)发射，基于射线结果正演和波形反演结果的正演波形对比.对比图8a和图8b发现，对数波形反演的相对介电常数结果相对于走时反演结果变化不大，这主要是因为走时反演得到的相对介电常数结果已经较为准确.但需要注意的是，对比图9a和图9b发现，波形反演得到的波形相对于基于射线结果正演得到的波形，与实际数据波形之间的相位符合更好.这说明，波形反演在走时反演的基础之上仍有提高，从而得到更加准确的相对介电常数分布.对比图8c和图8d，波形反演得到的电导率结果较重心频率下降法得到的电导率结果有明显的提高.无论是波形反演结果还是射线结果，都能明显观察到深度28 m位置处的地下异常体，而波形反演得到的电导率结果呈现了更多的细节.另外，波形反演得到的相对介电常数在异常体内部表现出了一个条带状的较低介电常数区域，与波形反演得到的电导率结果在相同位置处具有同样的特征.由于缺乏对应的地质信息，无法判断异常体的具体类型.需要注意的是，尽管对实际数据做了三维校正，但反演结果仍受一些因素的影响(如反演的多解性，噪声以及天线等)，因此反演结果中的一些细节变化并不一定可靠，需通过波形对比来判断反演结果整体的好坏.从图9c也能直观地看出，波形反演的结果无论是在相位还是振幅上都比射线结果更加贴近实际数据.因此，波形反演得到的结果更加准确，而且相对介电常数和电导率之间的符合较好.因此，对数波形反演方法在实际数据处理中的应用结果表明，该方法优于传统的射线类反演方法.

4总结与讨论

本文详细推导了对数目标函数下频率域探地雷达波形反演层析成像方法，与地震波形反演通过对目标函数和波动方程求导来得到梯度表达式不同，本文借鉴了Meles等的扰动理论推导梯度，并指出频率域梯度表达式中Re的意义是时间域波形反演梯度公式中体现不出的.使用离散傅里叶变换(DFT)将每次正演的时间域数据转换到频率域的方法只增加极少量的计算量，避免了巨量时间域数据的存储，有效减少计算机内存需求.在计算残场源时，为了避免高频无用信号的干扰，提出只使用以当前反演频率为中心的一个窄频带数据即可.在频率迭代策略上，文中采用串行频率策略，并且为了加速收敛每迭代10次则反演频率增加10 MHz.不同于地震波形反演每个频点都反演多次，本文每个频点只进行一次反演，这有两点原因：一是文中每次反演频率只增加很少(2 MHz)，反映在波长上变化微弱；二是每次反演过程中都计算迭代步长，保证反演更有效地收敛.文中三个算例也证明本文的频率策略是可行的.

图8　贵州实际数据反演结果(a) 走时反演得到的相对介电常数； (b) 对数波形反演得到的相对介电常数； (c) 重心频率下降法得到的电导率； (d) 对数波形反演得到的电导率Fig.8　Inversion results of field data from Guizhou(a) Permittivity results from first-arrival times method; (b) Permittivity results of logarithmic waveform inversion; (c) Conductivity results from applying centroid frequency downshift method; (d) Conductivity results of logarithmic waveform inversion.

图9　贵州实际数据反演结果的波形对比(a) 黑线和蓝线分别为实际数据波形和基于射线模型的正演波形； (b) 黑线和红线分别为实际数据波形和最终全波形反演结果对应的波形； (c) 蓝线和红线分别为(a)中黑线与蓝线的差和(b)中黑线和红线的差.所有数据都根据实际数据的最大振幅归一化.Fig.9　Transmitter gathers generated by the source placed at a 19 m depth in Fig.8(a) Blue and black lines show radar traces generated from results of ray tomograms and field data; (b) Red and black lines show radar traces generated from results of logarithmic waveform inversion and field data; (c) Blue and red lines show difference between blue and black lines in (a) and between red and black lines in (b), respectively. Amplitudes in all panels are normalized with respect to maximum amplitude of field data.

合成数据的反演结果证明对数目标函数下波形反演优于传统目标函数下波形反演，原因是使用对数目标函数时，波场残差受正演波场的自然比例调节作用.尽管如此，由于在推导过程中相位存在假设，使用对数目标函数的探地雷达波形反演对介电常数初始模型的要求较高.在实际数据处理中，数据的三维校正和源子波估计仍是重点，另外需要尽可能准确地选择初始模型来保证反演过程收敛.

未来我们需要关注探地雷达三维波形反演，其中FDTD仍将发挥重要作用.另外初始模型的获取可用Laplace域波形反演及Laplace-Fourier域波形反演替代传统的射线理论反演，从而获得更可靠的初始模型.在频率域探地雷达波形反演中波场正演方法、频率选择策略、目标函数设置方式、源子波估计等问题依然需要进一步的研究.

致谢感谢康涅狄格大学土木与环境工程学院刘澜波老师提供重心频率下降法的程序.

References

Cai W Y, Qin F H, Schuster G T. 1996. Electromagnetic velocity inversion using 2-D Maxwell′s equations.Geophysics, 61(4): 1007-1021.

Chung W, Ha T, Ha W, et al. 2007. Robust seismic waveform inversion using back-propagation algorithm.∥ 77th Annual International Meeting, Expanded Abstracts: 1780-1784.

Ernst J R, Maurer H, Green A G, et al. 2007a. Full-waveform inversion of crosshole radar data based on 2-D finite-difference time-domain solutions of Maxwell′s equations.IEEETransactionsonGeoscienceandRemoteSensing, 45(9): 2807-2828. Ernst J R, Green A G, Maurer H, et al. 2007b. Application of a new 2D time-domain full-waveform inversion scheme to crosshole radar data.Geophysics, 72(5): J53-J64.

Fu L, Liu S X, Liu L B, et al. 2014. Airborne ground penetrating radar numerical simulation and reverse time migration.ChineseJ.Geophys. (in Chinese), 57(5): 1636-1646, doi: 10.6038/cjg20140526.

Kuroda S, Takeuchi M, Kim H J. 2005. Full waveform inversion algorithm for interpreting cross-borehole GPR data.∥ 75th Annual International Meeting, SEG, Expanded Abstracts: 1176-1179. Liu L B, Lane J W, Quan Y L. 1998. Radar attenuation tomography using the centroid frequency downshift method.JournalofAppliedGeophysics, 40(1-3): 105-116.

Liu S X, Sato M. 2002. Electromagnetic logging technique based on borehole radar.IEEETransactionsonGeoscienceandRemoteSensing, 40(9): 2083-2092.

Liu S X, Wu J J, Zhou J F, et al. 2011. Numerical simulations of borehole radar detection for metal ore.IEEEGeoscienceandRemoteSensingLetters, 8(2): 308-312.

Liu S X, Lei L L, Fu L, et al. 2014. Application of pre-stack reverse time migration based on FWI velocity estimation to ground penetrating radar data.JournalofAppliedGeophysics, 107: 1-7. Meles G A, van der Kruk J, Greenhalgh S A, et al. 2010. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to-surface GPR data.IEEETransactionsonGeoscienceandRemoteSensing, 48(9): 3391-3407.

Pettinelli E, di Matteo A, Mattei E, et al. 2009. GPR response from buried pipes: Measurement on field site and tomographic reconstructions.IEEETransactionsonGeoscienceandRemoteSensing, 47(8): 2639-2645.

Pratt R G. 1990. Inverse theory applied to multi-source cross-hole tomography, Part 2: Elastic wave-equation method.GeophysicalProspecting, 38(3): 311-329. Pratt R G, Worthington M H. 1990. Inverse theory applied to multi-source cross-hole tomography, Part 1: Acoustic wave-equation method.GeophysicalProspecting, 38(3): 287-310.

Pratt G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion.GeophysicalJournalInternational, 133(2): 341-362.

Pratt R G. 1999. Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale

model.Geophysics, 64(3): 888-901.

Pratt R G, Shipp R M. 1999. Seismic waveform inversion in the frequency domain, Part 2: Fault delineation in sediments using crosshole data.Geophysics, 64(3): 902-914.

Shin C, Min D J. 2006. Waveform inversion using a logarithmic wavefield.Geophysics, 71(3): R31-R42.

Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies.Geophysics, 69(1): 231-248. Song Z M, Willianson P R, Pratt R G. 1995. Frequency-domain acoustic-wave modeling and inversion of crosshole data: Part Ⅱ: Inversion method, synthetic experiments and real-data results.Geophysics, 60(3): 796-809.

Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation.Geophysics, 49(8): 1259-1266.

Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data.Geophysics, 51(10): 1893-1903.

Wang F, Liu S X, Qu X X, et al. 2013. Crosshole radar traveltime tomography without ray tracing using the high accuracy fast marching method.ChineseJ.Geophys. (in Chinese), 56(11): 3896-3907, doi: 10.6038/cjg20131131.

Wang Z L, Zhou H, Li G F. 2007. Inversion of ground-penetrating radar data for 2D electric parameters.ChineseJ.Geophys. (in Chinese), 50(3): 897-904.

Williamson P R, Worthington M H. 1993. Resolution limits in ray tomography due to wave behavior: Numerical experiments.Geophysics, 58(5): 727-735.

Wu J J, Liu S X, Li Y P, et al. 2014. Study of cross-hole radar tomography using full-waveform inversion.ChineseJ.Geophys. (in Chinese), 57(5): 1623-1635, doi: 10.6038/cjg20140525. Zhou H, Chen H M, Li Q Q, et al. 2014. Waveform inversion of ground-penetrating radar data without needing to extract exciting pulse.ChineseJ.Geophys. (in Chinese), 57(6): 1968-1976, doi: 10.6038/cjg20140627. Zhou H, Sato M, Takenaka T, et al. 2007. Reconstruction from antenna-transformed radar data using a time-domain reconstruction method.IEEETransactionsonGeoscienceandRemoteSensing, 45(3): 689-696.

附中文参考文献

傅磊, 刘四新, 刘澜波等. 2014. 机载探地雷达数值模拟及逆时偏移成像. 地球物理学报, 57(5): 1636-1646, doi: 10.6038/cjg20140526.

王飞, 刘四新, 曲昕馨等. 2013. 基于HAFMM的无射线追踪跨孔雷达走时层析成像. 地球物理学报, 56(11): 3896-3907, doi: 10.6038/cjg20131131.

王兆磊, 周辉, 李国发. 2007. 用地质雷达数据资料反演二维地下介质的方法. 地球物理学报, 50(3): 897-904.

吴俊军, 刘四新, 李彦鹏等. 2014. 跨孔雷达全波形反演成像方法的研究. 地球物理学报, 57(5): 1623-1635, doi: 10.6038/cjg20140525.

周辉, 陈汉明, 李卿卿等. 2014. 不需提取激发脉冲的探地雷达波形反演方法. 地球物理学报, 57(6): 1968-1976, doi: 10.6038/cjg20140627.

(本文编辑何燕)

Frequency domain waveform inversion of cross-hole GPR data based on a logarithmic objective function

MENG Xu, LIU Si-Xin*，FU Lei, WANG Xian-Nan, LIU Xin-Tong, WANG Wen-Tian, CAI Jia-Qi

CollegeofGeoExplorationScienceandTechnology,JilinUniversity,Changchun130026,China

AbstractGround penetrating radar (GPR) tomography plays an important role in geology, hydrogeology and engineering investigations. Traditional tomography (i.e., the first-arrival times and maximum first-cycle amplitudes) based on ray theory cannot provide high-resolution images because only a fraction of the information contained in the radar data is used in the inversion. In recent years, waveform inversion is one of the biggest concerns because it can provide sub-wavelength resolution images. Waveform inversion has been applied in GPR over ten years, but most of the results are computed in the time domain. In the frequency domain, the choice of inverted frequencies is flexible and different types of objective functions can be used, therefore the results of frequency-domain waveform inversion are more diversified than that of the time domain.

KeywordsWaveform inversion; Logarithmic objective function; Permittivity; Conductivity; Cross-hole radar

基金项目国家高技术研究发展计划(2013AA064603),国家自然科学基金(40874073，41074076)资助.

作者简介孟旭，男，1987年生，博士研究生，主要从事探地雷达数据处理与解释、电磁波数值模拟及全波形反演的研究.E-mail：mengxu519@126.com*通讯作者刘四新，男，1966年生，山西太谷人，日本东北大学工学博士，博士生导师，主要从事探地雷达、钻孔雷达及电磁波测井等的方法理论和应用方面的研究.E-mail：liusixin@jlu.edu.cn

doi:10.6038/cjg20160530 中图分类号P631

收稿日期2015-05-26，2016-03-04收修定稿

孟旭， 刘四新， 傅磊等.2016. 基于对数目标函数的跨孔雷达频域波形反演.地球物理学报，59(5):1875-1887,doi:10.6038/cjg20160530.

Meng X, Liu S X, Fu L, et al. 2016. Frequency domain waveform inversion of cross-hole GPR data based on a logarithmic objective function.ChineseJ.Geophys. (in Chinese),59(5):1875-1887,doi:10.6038/cjg20160530.