超细颗粒在声波作用下团聚的数值模拟

郑建祥，康文瑶，吕辛桐

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)

超细颗粒在声波作用下团聚的数值模拟

郑建祥，康文瑶，吕辛桐

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)

摘要：在内径为0.11 m，高为1.5 m的团聚室中，以空气和燃煤飞灰超细颗粒为气相和固相，运用商业模拟软件FLUENT 14.0，通过自编C语言程序，将声场模型和FLUENT 14.0的传统模型结合，研究了涡片、声频率、声压级和颗粒初始浓度，分析了声波对超细颗粒团聚效率的影响。结果表明：加入涡片和增大飞灰颗粒初始浓度能够明显的增大颗粒的碰撞频率，从而增大颗粒的团聚效率；声频率对超细颗粒团聚效率的影响不是线性的，存在最佳频率为1 400 Hz-1 600 Hz；声压级越大，团聚效果越好，考虑到能耗问题，声压级取140 dB-160 dB。

关键词：超细颗粒；燃煤飞灰；声波团聚；粒径分布

工业生产特别是燃烧过程产生大量的超细颗粒，危害很大[1]。这些细颗粒物，尤其是PM10和PM2.5(粒径小于10 μm和2.5 μm的超细颗粒)，比表面积大、可携带重金属和细菌等有害物质，并能随呼吸进入人体肺部，具有极强的危害性。因此，对超细颗粒物的控制意义。目前广泛使用的旋风分离器、静电除尘器和布袋除尘器等虽然可以达到很高的脱除效率，但是其缺点是对超细颗粒的除尘效率较低。[2-3]如果能在燃烧和燃后区将这些细小颗粒团聚形成较大的颗粒，就可使其被现有的除尘装置所捕捉，就可以减少烟尘的排放。

声波团聚是一种有效的去除细颗粒物的预处理方法。利用声波对燃煤烟气的辐射效应，使细颗粒发生团聚，改变粒径分布，增加飞灰颗粒的平均粒径，从而提高超细颗粒在除尘器中的脱除效率。为了将声波团聚技术应用于燃煤电站等工业排放领域，需要采用燃煤飞灰等超细颗粒做为研究对象。Hoffmann等人[4]使用44Hz等极低频率的声波，同时添加石灰石颗粒作为团聚核，获得了比较好的团聚效果。这些实验均采用固定的声频率，因此无法研究频率对声波团聚的影响。国内也有相关的研究，姚刚等人[5]采用了频率为1 413 Hz和3 000 Hz的声波进行团聚实验，结合理论计算得出最佳频率为30 kHz。陈厚涛等人[6]使用1 kHz的声波，用燃煤飞灰做颗粒源，使得超细颗粒的脱除效率达到60%以上。徐鸿等人[7]在实验研究中发现，针对燃煤飞灰在声频率为2.9 kHz时获得最佳团聚频率。由以上可见，由于声波对于超细颗粒团聚的复杂性，从而使研究者们仍未得出一致的结论。本文以燃煤飞灰超细颗粒做为数值模拟中的颗粒源，采用双流体模型和颗粒群平衡模型对超细颗粒在声波作用下团聚流动过程进行数值模拟研究，研究涡片和各操作参数对声波团聚的影响。

1气固两相流数学模型及边界条件

1.1数学模型

由于团聚室内只充满气体相和固体相，流体力学参数需要经过颗粒体积分数而进行矫正。固体颗粒相与颗粒相之间的作用和气体相与固体颗粒相之间的相互作用应通过颗粒粘度和气固之间的曳力进行耦合。控制方程如下：

(1)质量守恒方程

气相：

(1)

固相：

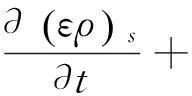
(2)

上述两表达式中，ε为气体相和固体相的体积分数；ρ为气体相和固体相的密度；u为各方向上的速度矢量；g为气体相；s为固体相。由于在气固两相流动中，团聚室内只存在固体相和气体相，所以在团聚室内气相和固相的体积分数之和等于1，即

εg+εs=1 .

(3)

(2)动量守恒方程

气相：

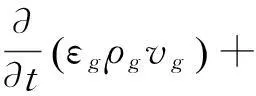
(4)

固相：

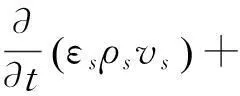
(5)

式中：τ为应力张量；g为重力加速度(m/s2)；P为压力(Pa)；β为曳力系数；vg为气相速；vs为固体颗粒相速度。

其中，固体颗粒相与气体相之间的应力张量如下所示：

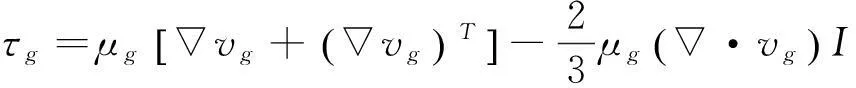
(6)

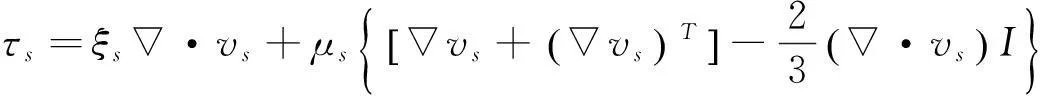
(7)

上述表达式中，I为单位张量； μg为气体剪切粘度，其中μg=μ1+μt；湍流黏性系数为

(8)

式中：ξs为固体体积粘度，在本文中选用Lun[8]模型。其表达式为

(9)

式中：μs为固体颗粒相的剪切粘度，它包括颗粒碰撞粘性、颗粒动力粘性和颗粒摩擦粘性：μs=μcollision+μkinetic+μfriction。颗粒碰撞粘性表达式如下：

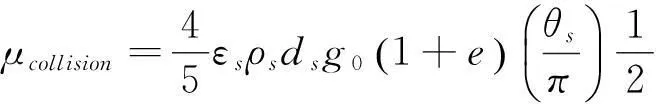
(10)

对于颗粒的动力粘性，本文采用Gidaspow提出[9]的表达式：

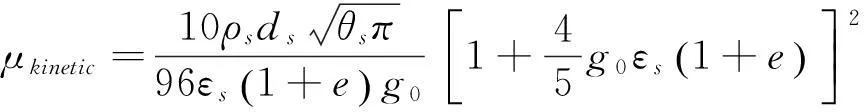
(11)

对于颗粒的摩擦粘性，本文采用Schaeffer模型[10]表示：

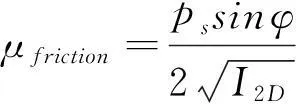
(12)

(3)固相脉动能量方程

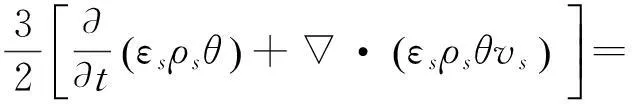
(13)

式中：θ为颗粒温度；c为颗粒脉动速度；ks为固相热传导系数；γs为颗粒间碰撞能量耗散率[11]：

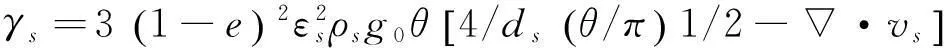
(14)

1.2颗粒群平衡模型

在工程领域的绝大部分实际工况中，颗粒场在空间上是各向异性的。如果依旧用零维颗粒群模拟描述，数值求解后只能得到某一时刻后颗粒尺度分布的大小，不能得到颗粒尺度分布与空间位置的关系，与实际物理过程不符。故此时需要把零维颗粒群平衡模拟与多相流模型耦合起来，形成一种新的模拟方法——多维颗粒群平衡模拟。多维颗粒群平衡方程(PBE)：

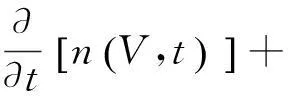
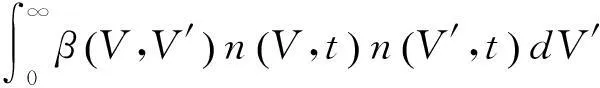
(15)

求解颗粒群平衡方程的主流方法有三种，即分区方法、矩方法和MonteCarlo法。考虑到计算量和计算精度的问题，本文选择分区法对颗粒群平衡方程求解，分区法通过把颗粒尺度分布曲线进行离散。针对每个离散区间建立某个颗粒尺度谱整体参数的平衡方程，然后对这些普通差分方程进行联立求解。

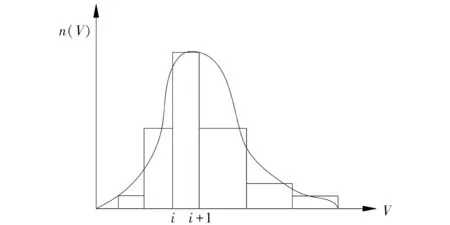
图1　颗粒尺度分布曲线离散图

假定颗粒相中颗粒的体积范围为V0—VN，按图1对颗粒相进行离散分组，将其分成(N+1)个不同的粒径，共划分为N个颗粒组，分组编号依次为0，1，…，N-1，则第i组颗粒的数目ni及体积分数αi分别为

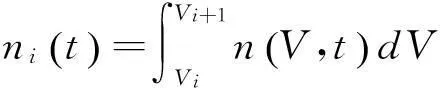
(16)

αi=niVi，

(17)

式中：Vi为第i组颗粒体积，i=0，1，…，N-1；αi为第i组颗粒的体积分数。

将公式(16)、公式(17)代入公式(15)，将其变换成与αi有关的方程：

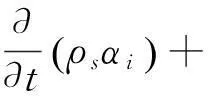
(18)

式中：ρs为颗粒相密度；ui为第i组颗粒速度。

为求解公式(18)，还需根据颗粒相的分组情况对Bag，i、Dag，i进行离散化处理，如下：

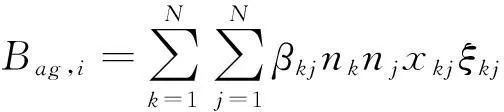
(19)

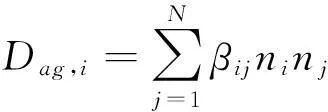
(20)

其中，βij为颗粒i和颗粒j的湍流聚并系数；当Vi

1.3声波团聚

颗粒团聚引起的粒径分布变化可用离散化的气溶胶动力学方程计算：

(21)

式中:ni，nj，nk分别为第i，j，k组的颗粒浓度；Kij为团聚核函数，其物理意义是单位浓度的颗粒和在单位时间内发生碰撞的次数。

声波团聚的机理是在声场作用下，使颗粒之间发生相对运动，从而增加颗粒的碰撞频率。对于超细颗粒而言，范德华力和静电引力起主要作用，碰撞后极易粘在一起，发生团聚。在声场中，气体介质随着声波周期性振荡，其中的颗粒也不同程度地被带动，颗粒与气体介质振幅的比值称为挟带系数，可用公式(22)计算：

(22)

式中：ω为声波角频率；τ为颗粒的弛豫时间。

声波团聚过程很复杂，涉及的机理很多，包括同向团聚机理、流体力学作用、声流和声致湍流等。其中，同向团聚机理是最重要的机理，指的是不同大小的颗粒在声场中随声波振动的幅度不同，颗粒间产生相对运动，从而导致颗粒团聚。同向团聚机理的核函数可由公式(23)计算：

(23)

式中：di和dj为颗粒直径；ug为气体介质中声波引起的振动速度幅值；μg为颗粒与介质之间运动的速度差与声波振动速度ug的比值；Eij为碰撞效率。

图2　团聚室二维模型尺寸图

1.4边界条件

团聚室的模拟对象如图2所示，团聚室高度H为1.5 m，内径D为0.11 m。计算采用双流体模型计算气相和颗粒相运动情况，用标准k-ε模型作为湍流模型，采用颗粒群平衡模型计算颗粒聚并情况，并在模型中加入编写的关于声场UDF程序计算颗粒在声波作用下颗粒团聚情况。初始颗粒尺度分布由静电低压撞击器从某电厂除尘器前烟道测得，颗粒尺度分布在0.021 μm-6.256 μm之间的12个区间，如表1所示。入口为速度入口，流速取0.25 m/s-0.5 m/s，空气黏度1.48×10-5m2/s，空气密度1.225 kg/m3，颗粒相密度2 100 kg/m3，出口条件采用压力出口，壁面采用无滑移边界条件。

表1　各尺度颗粒体积分数

图3　涡片对团聚效果的影响

2结果与讨论

2.1涡片对团聚的影响

加入涡片对燃煤飞灰中颗粒各级粒径分布的影响，如图3所示。其中烟气速度为0.45 m/s，烟气浓度为0.46 kg/m3，声频率为1 600 Hz，声压级为120 dB。由图3的模拟结果可知，在Bin-3(即颗粒粒径d=3.074 μm)之前(等于Bin-3)无涡片的各级颗粒体积分数要稍高于有涡片的各级颗粒，而在Bin-3后有涡片的各级颗粒体积分数明显偏高。该现象表明在超细颗粒团聚过程中，加入涡片具有更优的的团聚效果。涡片是常用的产生扰流的装置，它可以产生小尺度湍流，通常以涡的形式存在。当烟气流经这些小尺度涡流区域时，颗粒之间的碰撞率得到提高，从而使颗粒的团聚效率进一步增强。

2.2声频率对声波团聚的影响

频率对声波团聚前后燃煤飞灰颗粒各级粒径分布的影响，如图4所示。其中，初始烟气流速为0.45 m/s，浓度为0.46 kg/m3，声压级分别是120 dB，130 dB，140 dB，150 dB，160 dB。

图4　声频率对声波团聚颗粒粒径分布的影响

对比图4的模拟结果可见，频率对声波团聚效率的影响并不呈简单的线性关系，而是存在某一最佳频率，此时声波团聚效果最佳。超细颗粒粒径小于3.074 μm时，各级颗粒粒径的体积分数随频率的增大而减小。在频率大于某一值时，各级颗粒粒径的体积分数增大。分析图4(a)，当声压级保持在120 dB的较低水平，频率为1 600 Hz时，超细颗粒粒径大于3.074 μm(等于3.074 μm)的体积分数最多，团聚效率最高；观察图4(b)、图4(c)和图4(e)，当声压级分别上升到130 dB、140 dB、160 dB，频率为1 400 Hz时，超细颗粒粒径大于3.074 μm(等于3.074 μm)的体积分数最多，团聚效果最好。声压级为150 dB，频率为1 600 Hz时，超细颗粒粒径大于3.074 μm(等于3.074 μm)的体积分数最多，团聚效果最佳。

燃煤飞灰声波团聚效率对频率是敏感的，保持声压级和煤飞灰初始浓度等条件不变时，存在唯一的最佳频率使声波团聚效率最好，若频率偏离最佳频率，则团聚效率下降。按照同向团聚机理，当声波频率过低时，所有顆粒在声场中完全振荡，不能产生相对运动；若声波频率过高，则颗粒在声场中保持相对静止，不存在相对运动，也不产生团聚。因此，声频率对声波团聚效率的影响不是线性的，声压级的大小也会影响最佳频率的取值，声压级增大时，最佳频率的值有减小的趋势。

2.3声压级对声波团聚的影响

声压级对声波团聚前后燃煤飞灰颗粒各级粒径分布的影响，如图5所示。其中，初始烟气流速为0.45 m/s，浓度为0.46 kg/m3，声频率分别是1 100 Hz，1 400 Hz，2 000 Hz。

图5　声压级对声波团聚颗粒粒径分布的影响

从图5可见，当气燃煤烟气的初始浓度、速度和声源频率一定时，声压级增大，超细颗粒在粒径小于3.074 μm时，各级颗粒粒径的体积分数减小，但超细颗粒在粒径大于3.074 μm(等于3.074 μm)的各级颗粒粒径的体积分数增大，即各级颗粒碰撞的结果是大颗粒增多，小颗粒减少，声波团聚效果就越佳。因为，气体介质中的超细颗粒振动幅度随着声压级上升而增大，增加了颗粒间的相对运动，从而提高了颗粒的碰撞效率。

声压级对可燃煤烟气中超细颗粒颗粒团聚的影响可归结为两方面原因。其一，在空气声场中，声压级SPL表示为

(24)

(25)

公式(24)中，prms为声压的均方根；pref为基准压力；公式(25)中，Pg为声压的绝对值，Pg=ρgc0Ug(其中，ρg为气体密度)；c0为声速；Ug为质点速度幅值。SPL增大，质点振动速度增大，颗粒被夹带振幅增大，颗粒在一个声波周期内作用的有效体积增加，增大了与其它颗粒的碰撞频率，从而提高团聚效率。其二，颗粒在声场中的运动速度为

(26)

当颗粒被夹带的振幅大于团聚室半径时，颗粒将与团聚室壁面碰撞导致能量损失。因此，声压较高时，颗粒团聚效率增幅逐渐变小。声压级越高，越有利于小颗粒的团聚[12]，因此颗粒的团聚效率仍保持增加的趋势。

2.4飞灰颗粒的初始浓度对声波团聚的影响

颗粒初始浓度对燃煤飞灰中颗粒各级粒径分布的影响，如图6所示。其中，烟气速度为0.45 m/s，声频率为1 600 Hz，声压级为120 dB，飞灰颗粒的初始浓度分别为0.46 kg/m3，0.5 kg/m3，0.6 kg/m3。

图6　飞灰颗粒初始浓度对声波团聚颗粒粒径分布的影响

由图6的模拟结果可知，其他条件一定时，超细颗粒初始浓度越高，燃煤飞灰颗粒在粒径小于3.074 μm时，各级颗粒粒径的体积分数越小，而粒径大于3.074 μm(等于3.074 μm)的各级粒径的体积分数越大，即声波团聚效过越好。这是因为飞灰颗粒浓度较低时，超细颗粒间距较大，则在声波作用下颗粒就需要较长的时间才能相互接近和作用，因此碰撞频率较低，声波团聚效果变差。飞灰颗粒初始浓度对声波团聚效果的影响可以对声波团聚效率的增幅随着团聚时间的推移逐渐减少的现象进行解释。随着团聚过程的进行，空间内总颗粒数目逐渐降低，团聚效果逐渐变差。在工业的应用中，声波团聚可以作为一种比较经济的预处理方法，使含尘烟气中的超细颗粒变大，然后用常规的除尘方法来进行下一步的处理，以达到控制超细颗粒排放的目的。

4结论

本文通过数值模拟研究了燃煤飞灰超细颗粒在声波作用下团聚的效果。在声波的作用下，超细颗粒粒径发生明显变化，大量小颗粒碰撞产生了大颗粒。本文研究了单一因素对声波团聚效果的影响，模拟的结果表明：加入涡片和增大飞灰颗粒初始浓度能够明显的增大颗粒的碰撞频率，从而增大颗粒的团聚效率；频率是最重要的影响参数，对超细颗粒团聚效率的影响不是线性的，而是存在最佳频率，范围一般为1 400 Hz-1 600 Hz；声压级越大，团聚效率越高，考虑到能耗问题，声压级通常取140 dB-160 dB。

参考文献

[1]Garcia-Nieto P J.Study of the evolution of aerosol emissions from coal-fired power plants due to coagulation，condensation，and gravitational settling and health impact[J].Journal of Environmental Management，2006，79(4)：372-382.

[2]E.Riera-Franco de Sarabia，J A Gallego-Juarez，G Rodriguez-Corral，L Elvira-Segura，I Gonzalez-Gomez.Application ofhigh-power ultrasound to enhance fluid/solid particle separation processes[J].Ultrasonics，2000，38(1-8)：642-646.

[3]Hoffmann T L.Environmental implication of acoustic aerosol agglomeration[J].Ultrasonics，2000，38(1-8)：353-357.

[4]Hoffmann T L，Chen W，Koopmann G H，Scaroni A W，Song L.Experimental and numerical analysis of bimodal acoustic agglomeration[J].Journal of Vibration and Acoustics，1993，115：232-240.

[5]姚刚，赵兵，沈湘林.燃煤可吸入颗粒物声波团聚效果的实验研究和数值分析[J].热能动力工程，2006，20(2)：175-178.

[6]陈厚涛，赵兵，徐进，等.燃煤飞灰超细颗粒物声波团聚清除的实验研究[J].中国电机工程学报，2007，27(35)：28-32.

[7]徐鸿，骆仲泱，王鹏，徐飞，岑可法.声波团聚对燃煤电厂可吸入颗粒物的排放控制[J].浙江大学学报：工学版，2007，41(07)：1168-1171.

[8]C.K.K.Lun，S.B.Savage，D.J.Jeffrey.Kinetic theories for granular flow：Inelastic particles in couette flow and slightly inelastic particles in a general flow field[J].J Fluid Mech，1984，140：223-256.

[9]D.Gidaspow，R.Bezburuah，J.Ding.Hydrodynamics of circulating fluidized beds，kinetic theory approach[J].Engineering，1992(2)：75-82.

[10] D.G.Schaeffer.Instability in the evolution equations describing in compressible granular flow[J].Journal of Differential Equations，1987，66(11)：19-50.

[11] 郑建祥，朱秀丽.粘附性颗粒流化物特性研究及信息熵分析[J].东北电力大学学报，2015，35(2)：18-22.

[12] 姚刚，沈湘林.基于分形的超细颗粒声波团聚数值模拟[J].东南大学学报：自然科学版，2005，35(1)：145-148.

Numerical Simulation on Agglomeration of Ultrafine Particles Under the Effect of Acoustic

ZHENG Jian-xiang，KANG Wen-yao，LU Xin-tong

(Energy Resource and Power Engineering College，Northeast Dianli University，Jilin Jilin 132012)

Abstract：A agglomeration-room，0.11m in diameter and 1.5m in height，was employed to investigate systematical in effect of acoustic wave on agglomeration efficiency of ultrafine particles.The vortex sheet，sound frequency，sound pressure level and initial particle concentration with air as gas phase and coal fly ash ultrafine particles as solid phases were simulated using CFD code Fluent14.0.The sound model what was compiled by C language program combined the developed model with CFD software.The simulation results show that adding vortex sheet and increase fly ash particles initial concentration can significantly increase of particle collision frequency，thereby increasing the aggregate efficiency.Sound frequency effect on the efficiency of agglomeration of ultrafine particles is not linear，existing an optimal frequency of 1400 Hz-1600 Hz.Sound pressure level is the higher，the agglomeration effect is the better.Taking into account the energy problem，the sound pressure level takes 140 dB-160 dB.

Key words：Ultrafine particles；Coal fly ash；Acoustic agglomeration；Particle size distribution

收稿日期：2016-04-12

作者简介：郑建祥(1977-)，男，福建省建瓯市人，东北电力大学能源与动力工程学院副教授，博士，主要研究方向：气固两相流动特性研究.

文章编号：1005-2992(2016)03-0026-08

中图分类号：TK16

文献标识码：A