潜器惯性类水动力参数计算方法研究*

高　峰　于秋礼

(1.91439部队　大连　116041)(2.中船重工第七一〇研究所　宜昌　443003)

潜器惯性类水动力参数计算方法研究*

高峰1于秋礼2

(1.91439部队大连116041)(2.中船重工第七一〇研究所宜昌443003)

摘要为精确获取潜器水动力参数，对惯性类水动力参数常用计算方法进行了总结，给出了方程解析法、半经验公式法和水池试验法优缺点。在对惯性水动力参数计算机计算方法研究的基础上，提出一种以Hess-Smith面元法为理论依据，获取潜器惯性类水动力参数的方法。编写惯性类水动力参数数值计算程序，计算结果与圆球、椭球，等简单几何体惯性类水动力参数理论值对比，证明计算方法及所编程序的正确性，并探讨了网格划分形式和网格数量对计算精度的影响。最后以复杂构型潜器为研究对象，计算其所受的惯性类水动力参数，与半经验公式结果比较及定性分析，得知数值计算结果更具合理性。

关键词边界元法; 水动力参数; 附加质量; 潜器

Class NumberTJ61+7

1引言

潜器近年来在军事、勘探、救援等领域得到广泛应用，潜器研究受到更多关注，潜器水动力特性是潜器研究重要课题之一。潜器的水动力特性对其整体布局、航行控制、能源需求、水下作业甚至布放回收均具有重要影响；同时潜器水动力参数获取也是其六自由空间动态仿真和运动控制的前提与基础；另外对潜器进行减振降噪研究也需考虑潜器的水动力特性。由此可见，潜器水动力参数的精确对潜器的研发与设计具有重要意义。

陈琪玮给出了辨识航行体水动力参数的智能计算方法[1]，施小成给出利用递推最小二乘法估计潜器水动力参数数学模型[2]，袁伟杰等提出了基于遗传算法的自治水下机器人水动力参数计算方法[3[4]，李天森和S K Lee等分别给出基于水池试验的水动力参数测量计算方法[5～6]。

本文以复杂潜器惯性水动力参数计算为研究对象，依据面元法理论，应用计算机数值计算方法对潜器惯性水动力参数获取进行了研究，可为潜器等相关装备设计应用提供参考。

2常用惯性类水动力计算方法

潜器水动力参数可分为两种：一是和加速度有关的惯性类水动力参数,即附加质量矩阵；二是和速度有关的粘性类水动力参数[7～10]。粘性类水动力参数可通过CFD软件模拟潜器拖曳水池和悬臂水池试验求得，并已取得良好的数值计算精度[8～10]。

潜器惯性类水动力参数常用计算方法归纳总结主要包括以下几种：方程解析、半经验公式、水池试验测量、数值计算。

2.1方程解析

利用流体力学理论求解解析值，目前除了球体、椭球体、圆柱体等简单构型几何体的惯性类水动力参数可直接由其绕流场的速度势求得外，复杂构型潜器的惯性类水动力参数则很难求得。

2.2半经验公式

半经验公式估算是一种较为粗糙的计算方法，它提供的水动力参数是在简单几何形体理论计算公式的基础上作一些修正得出的，或是根据在大量船模实验结果基础上经整理得出的半经验的图谱估算得到，在估算细长体时效果很好，但复杂构型潜器附体较多，外形各异，采用舰船、潜艇、鱼雷等提供的半经验公式，这不可避免地给潜器，尤其是复杂构型潜器的水动力参数估算带来了很大的误差。

2.3水池试验测量

水池试验测量惯性类水动力参数，常用的测量方式包括周期比较法、惯性法、电比拟法、平面运动机构等。但就当前来说，水池试验测量费用高，周期长、不利于潜器，尤其是低成本潜器的开发和研究。

2.4数值求解

随着计算机计算能力的不断提高，计算流体力学已成为流体力学研究中的一个重要分支和辅助解决工程问题有效手段。计算机数值求解的方法又可分为两种：一是运用商用集成计算软件求解，二是通过分析方程编程求解计算。

2.4.1商用集成计算软件

用于求解惯性类水动力参数的商业软件有很多，其中比较常见的有以下几种：AQWA、HYDROSTAR、MOSES、NEPTUNE、WADAM、WAMIT、WAVELOAD等，以上流体力学软件包(Hydrodynamic Software Packages)多用以时域和频域势流理论为基础，计算舰船以及海上平台波载作用下的水动力问题；惯性类水动力参数多应用频域势流理论求得[7]。

大型计算流体动力学软件(CFD)fluent等，利用其动网格技术使物体作振荡运动求物体的受力，可用于潜器的惯性类水动力参数的逐个计算[12～13]。但CFD建模相对复杂，划分网格困难，且对网格质量也有要求，否则使用动网格时会错误中止。而面元法网格只在潜器构型表面划分面元，建模相对简单，网格达到一定数量后，便可获得良好的计算精度；计算简便，一次可完成潜器36个惯性类水动力参数的全部计算，较CFD计算方法具有明显的优势。

此外气动力仿真软件系统USAERO也可用于惯性类水动力参数的获得，并取得了良好的计算精度[14]。

2.4.2编程数值计算求解

编程数值计算求解惯性类水动力参数的理论主要有两种：1)切片理论(Strip Theory)，基于波浪辐射与衍射沿潜器或舰船纵向方向的变化极其缓慢这一假定，对纽曼-开尔文方程(N-K方程)进行一定合理的简化，应用求解三维纽曼-开尔文方程(N-K方程)的近似方法计算。在假设潜器构型为细长体即潜器横向尺寸远小于纵向尺寸的前提下，其计算结果可以满足工程应用。但对于横截面沿纵向变化大的复杂构型潜器其假设不成立，计算精度大为降低。2)边界元法，将物体表面划分单元，在每一个单元上布置强度待定的基本解(像源、汇、偶极子等)，从而确定流场速度势，进而得到惯性类水动力参数。其中Hess-Smith面元法就是应用边界元法第三类方法：间接表达式进行求解的。将积分方程完全用微分方程的单位奇异解表示，奇异解对应的奇点以特定强度分布在感兴趣的边界上，奇点密度函数其本身并无具体的物理含义，但一旦从积分方程数值求出密度函数，但只要作一些积分计算就可以得到物体内任意一点处解参数的值。

Hess-Smith面元法求解数值计算理论假定流体为无粘、无旋、不可压缩的理想流体，这一假设与惯性类水动力参数的定义一致。运用Hess-Smith面元法计算复杂构型潜器的惯性类水动力参数在理论上可得到有力的支撑[15]。

3Hess-Smith面元法惯性类水动力计算方法

采用Hess-Smith面元法编程，其理论依据以及数值模型详细可参考文献[15～16]。这一方法用多平面四边形表面单元近似表示物面，每个单元上布置一强度未知的源，然后在物体表面的某些考察点上满足法向速度为零的物面边界条件，得到求单元源密度的线性代数方程组。求解方程组得到源密度分布，进而可求流场内任意点的速度、压力等物理量。因此Hess-Smith面元法计算程序计算精度仅与数值模型建立的精准有关。

3.1Hess-Smith面元法惯性类水动力程序计算流程

惯性类水动力数值计算程序以Hess-Smith面元法为计算核心，其计算流程如图1所示：可大致分为前处理、求解计算以及后处理三部分。

图1　惯性类水动力参数计算流程

其中前处理包括几何建模、网格划分、数据输入三部分：几何建模主要是在CAD软件中完成模型的建立；网格划分主要是完成Hess-Smith计算程序所需的面元网格划分；而数据输入则完成面元网格的整理以及Hess-Smith计算程序所需格式数据的准备工作。求解计算是整个程序的核心，综合考虑计算机硬件和数值计算时间和计算精度等方面的因素，计算程序目前最大面元网格数为5500。后处理主要包括结果输出和图形显示两部分：结果输出完成各面元网格的速度、压力等信息以及潜器整体的惯性类水动力参数及无量纲系数的输出；图形显示完成各面元上速度以及压力的显示，进而根据结果图可在压力或速度变化急剧的部位加密网格，对网格布局进行优化，进一步提高计算精度。

3.2Hess-Smith面元法惯性类水动力程序计算精度

为验证 Hess-Smith惯性类水动力计算程序的有效性和计算精度，建立圆球和椭球网格模型，同时为比较不同网格划分形式对计算精度的影响，圆球分别采用球对称和柱对称两种网格划分方式，其网格模型效果图分别如图2～图4所示。计算误差与网格数量之间的关系如图5、图6所示。

图2　圆球对称网格模型

图3　圆球柱对称网格模型

图4　椭球网格模型图

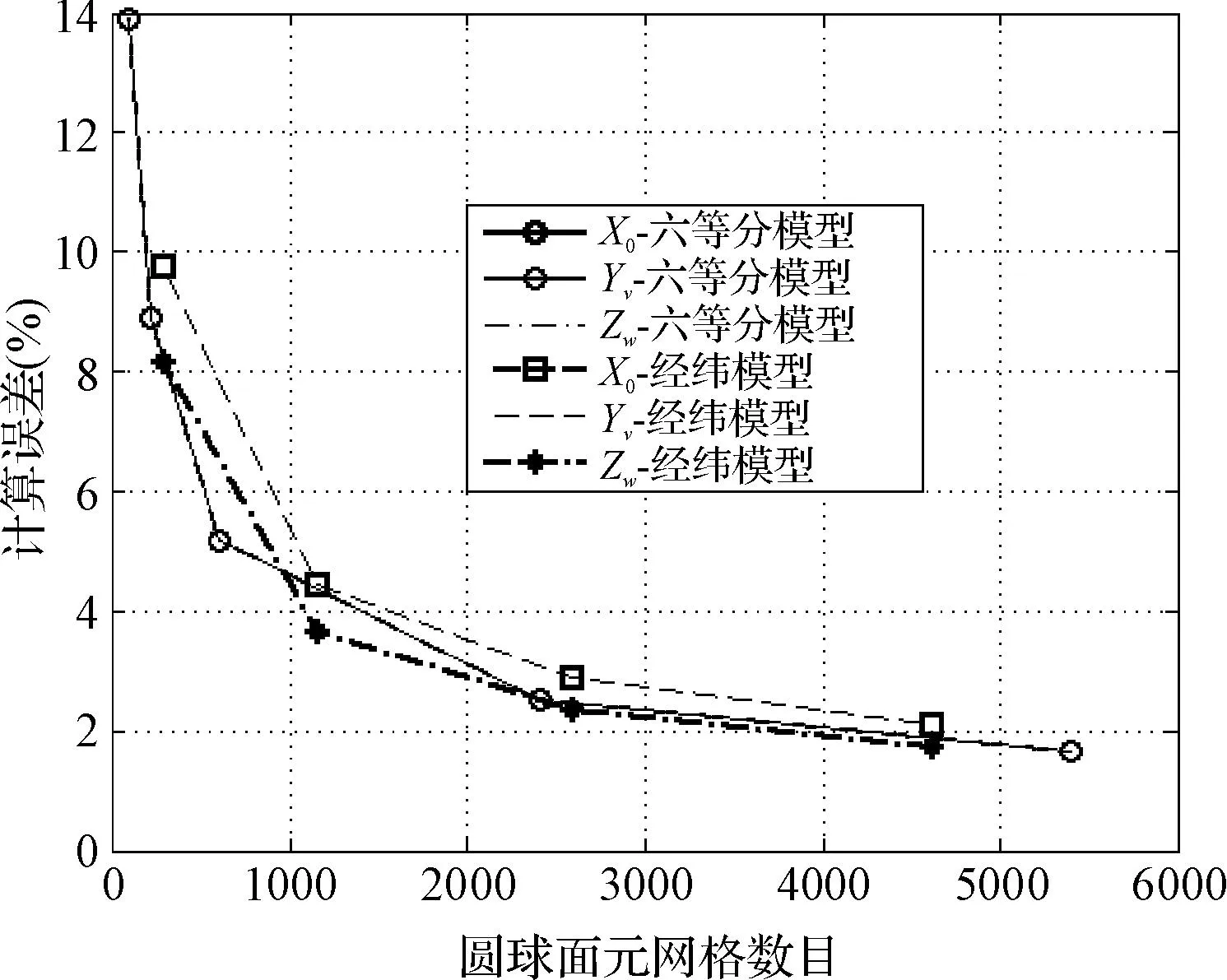
图5　圆球球对称模型与柱对称模型精度对比

图6　椭球网格数目与计算精度关系图

从图5可以看出，圆球柱对称网格模型各坐标轴上的网格划分的差异性导致理论上各轴方向本应相等的惯性水动力参数出现不等的数值计算结果，而球对称网格模型在网格划分上考虑圆球三轴的对称性，其各轴方向惯性水动力参数结算结果相等；从整体趋势上可以看出不管是球对称网格模型还是柱对称网格模型，其计算精度都随着网格数目的增多而不断提高；当网格达到一定数量后，再行增加网格的数量对计算精度的提高将不会有太大影响。此外从图6也可以看出，惯性类水动力参数的计算精度随着网格数量的增多而不断提高。且其计算精度与理论值相比误差不大于2%，计算精度良好，完全满足工程应用需要。

综上所述，可以得出以下两条基本结论：1)网格模型的划分要跟据实际模型的对称性对称划分；2)在计算机硬件和计算时间允许的前提下尽可能增大模型网格的数量，尽量对模型进行精细划分，尤其是在压力和速度变化急剧的面元部分，以提高数值计算精度。

3.3潜器Hess-Smith惯性类水动力计算结果以及分析

以一潜器为具体模型实例，对其进行惯性类水动力参数求解计算，其网格模型如图7所示，共计划分5374个面元网格，经计算其数值计算结果见表1。

图7　潜器网格模型

图8　潜器面元压力分布

表1　Hess-Smith面元法数值计算数据

表2　半经验公式计算数据

由于该潜器目前尚未进行水池水动力测量试验，其惯性类水动力参数仅通过半经验公式估算得到，但通过圆球、椭球计算结果精度以及上述定性的分析可知，Hess-Smith面元法数值计算结果数据应更可取。

4结语

本文通过对惯性类水动力参数计算方法优缺点的对比与归纳，以Hess-Smith面元法为理论依据编写数值计算程序，提供了一种精确计算潜器惯性类水动力参数的手段；通过简单模型的数值计算结果与理论值的对比，验证了计算方法和程序的有效性和准确性；通过对一潜器建模以及计算，得到了其惯性类水动力参数即附加质量矩阵，与半经验公式结果对比分析，数值计算结果更可取。但是本文没有考虑有限水深、自由液面、潜器附近物体等对潜器附加质量的影响，后续可作进一步分析与研究。

参 考 文 献

[1] 陈玮琪，颜开，王宝寿.辨识航行体水动力参数的智能方法[J].船舶力学，2011，15(4)：359-363.

[2] 施小成，赵俊成，周佳加.UUV水动力参数估计及深度自抗扰控制方法[J].仪器仪表学报，2014，46(11)：1-6.

[3] 袁伟杰，刘贵杰，朱绍峰.基于遗传算法的自治水下机器人水动和参数辨识方法[J].机械工程学报，2010，35(12)：96-100.

[4] 刘建成，刘学敏，徐玉如.极大似然法在水下机器人系统辨识中的应用[J].哈尔滨工程大学学报，2001，22(5)：1-4.

[5] 李天森.鱼雷操纵性[M].北京：国防工业出版社，1999：242-251.

[6] S K Lee,S J Cheon,T H Joung,T S Jang, J H Lee. Evaluation of the Added Mass for a Spheroid-type UUV by VPMM Test[C]//Proceedings of the Nineteenth (2009) International Offshore and Polar Engineering Conference，2009：703-709.

[7] 蒋新松，封锡盛.水下机器人[M].沈阳：辽宁科学技术出版社,2000:257-271.

[8] 胡志强,林扬,谷海涛.水下机器人粘性类水动力数值计算方法研究[J].机器人，2007，29(2)：145-150.

[9] 谷海涛,林扬,胡志强.带槽道桨水下机器人阻力特性的数值分析[J].微计算机信息，2007，23(14)：227-228.

[10] 康涛，胡克，胡志强等.CFX与USAERO的水下机器人操纵性仿真计算研究[J].机器人，2005，27(6)：535-538.

[11] A P McCabe. An Appraisal of a Range of Fluid Modelling Software[D]. U.K.：Department of Engineering Lancaster University，2004：18-48.

[12] 郭志彬，段文洋，赵彬彬.数值计算复杂构型潜器附加质量的方法[J]. 中国科技论文在线精品论文,2009, 2(5)：428-435.

[13] 马烨，单雪雄.数值计算复杂外形物体附加质量的新方法[J].计算机仿真，2007，24(5)：75-78.

[14] 程庆伟，张靖，李遗.气动力仿真软件系统USAERO的计算精度研究[C]//飞行力学与飞行试验学术交流年会论文集.中国航空学会.中国飞行试验研究院,2005:353-357.

[15] J L Hess，A M O Smith. Calculation of Potential Flow about Arbitrary Bodies[J] . Progress in Aeronautical Science,1967，8(8)：1-138.

[16] 戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京：国防工业出版社,1998:15-54.

Calculation Method of Inertial Hydrodynamic Parameters of Underwater Vehicle

GAO Feng1YU Qiuli2

(1.No.91439 Troops of PLA，Dalian116041)(2.No.710 R&D Institute, CSIC, Yichang443003)

AbstractIn order to predict maneuverability and motion simulation of underwater vehicle with complex configuration，it is necessary to derive the hydrodynamic parameters in advance. So this paper aims to determine the inertial hydrodynamics for the governing equations of motion for underwater vehicle. By summarizing and comparing several computational techniques used to deriving inertial hydrodynamics, a code which is based on Hess-Smith panel elements method is programmed as a useful tool for inertial hydrodynamics numerical calculation. The numerical results of an ellipsoid and sphere calculated by the code were confirmed by the data of the theoretical value, which gives confidence that this approach will be useful for calculating inertial hydrodynamics. Essentially, this paper is looking for a general answer as to how many panels are enough over a prescribed geometry in order to accurately capture the flow effects based on different panel results. Thus inertial hydrodynamics calculated by the approach is presented and compared with the semi-empirical value, which shows that the approach can be used to calculate the inertial hydrodynamics of the underwater vehicle with complex configuration.

Key Wordsboundary element method, hydrodynamic parameters, added mass, underwater vehicle

*收稿日期：2015年12月6日,修回日期：2016年1月18日

作者简介：高峰,男,工程师,研究方向：试验技术。

中图分类号TJ61+7

DOI：10.3969/j.issn.1672-9730.2016.06.033