样本估计总体思想的应用
2016-06-29陈德前
□陈德前
样本估计总体思想的应用
□陈德前
用样本特征去估计总体的特征是统计方法最基本的特点,这是因为有些被考察对象的总体数目太大,有些又具有破坏性,所以不能一一进行考察,而必须采用抽样的方法.样本虽然不能完全代表总体,但当选择的样本数据与样本容量得当时,用样本去估计总体就具有一定的可靠性.在实际生活中,我们常常利用样本估计总体的思想来解决有关问题,进行决策.
一、用样本的平均数估计总体的平均数
例1在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行统计,并绘制成如图1所示的统计图.
(1)求这50名同学捐款的平均数;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
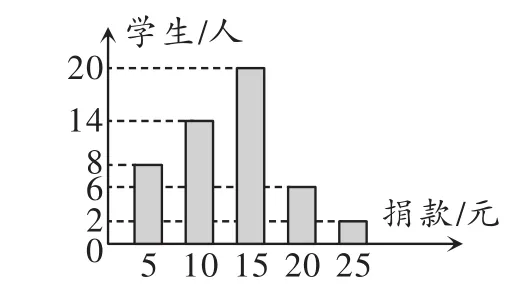
图1
解析:(1)这50名同学捐款的平均数为(5×8+ 10×14+ 15× 20+20×6+25×2)÷50=13(元);
(2)估计该校学生的捐款总数为13×600=7800(元).
点评:解决问题(2)的关键是先利用样本中捐款的平均数来估计总体中捐款的平均数,再用总体平均数乘以该校总人数即可得学生的捐款总数.
二、用样本的百分比估计总体的百分比
例2为了进一步了解义务教育阶段学生体质健康状况,教育部对我市某中学九年级的部分学生进行了体质抽测,体质抽测的结果分别为四个等级:优秀、良好、合格、不合格.根据调查结果绘制了如图2所示的两幅不完整的统计图,请你根据统计图提供的信息回答以下问题:
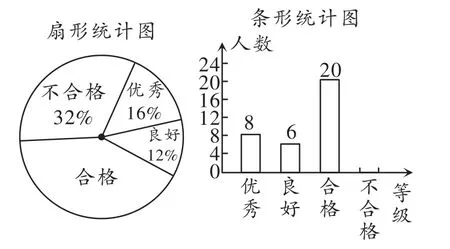
图2
(1)在扇形统计图中,“合格”的百分比为________;
(2)本次体质抽测中,抽测结果为“不合格”等级的学生有_____人;
(3)若该校九年级有400名学生,估计该校九年级体质为“不合格”等级的学生约有_______人.
解析:(1)合格的百分比为1-32%-16%-12%=40%;
(2)总人数=8÷16%=50人,不合格的人数=50×32%=16人;
(3)九年级体质不合格人数= 400×32%=128(人).
点评:本题解题的关键是从统计图中得出样本中体质抽测结果“不合格”的百分比,进而估计出学生400人中体质抽测结果“不合格”的百分比,再由此计算出体质“不合格”等级学生的具体人数.
三、用样本的频数(频率)估计总体的频数(频率)
例3某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙——我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图3所示的不完整条形统计图.
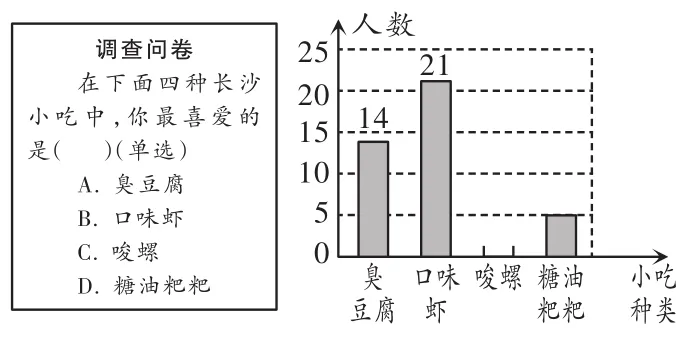
图3
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
解析:(1)根据题意得:喜欢“唆螺”的人数为:50-(14+21+5)= 10(人),补全统计图如图4所示.
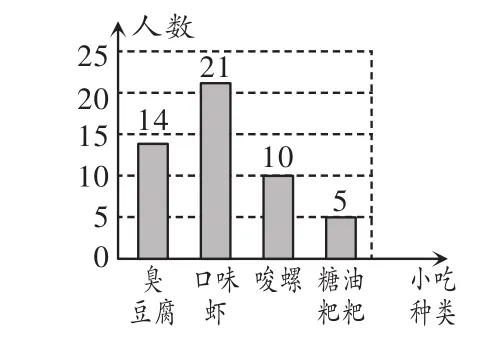
图4
点评:由样本中最喜爱“臭豆腐”的频率估计出总体中最喜爱“臭豆腐”的频率是解决第(2)题的关键.
四、用样本中特殊数据估计总体中相应特殊数据
例4为提高居民的节水意识,向阳小区开展了以“建设节水型社区,保障用水安全”为主题的节水宣传活动.小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,她在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图5所示.
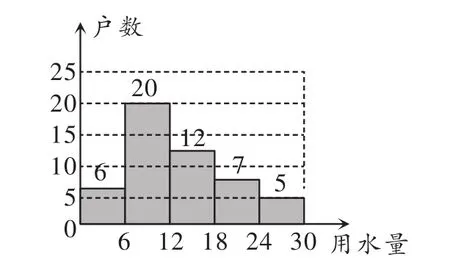
图5
(1)试估计该小区5月份用水量不高于12t的户数占小区总户数的百分比;
(2)把图中每组用水量的值用该组的中间值(如0~6的中间值为3)来替代,估计该小区5月份的用水量.
解析:(1)这50户5月份用水量不高于12t的户数占小区总户数的百分比为故估计该小区5月份用水量不高于12t的户数占小区总户数的百分比是52%;
(2)用各组的中间值乘以户数,得出总的用水量为3×6+9×20+ 15×12+21×7+27×5=660t,再除以抽查的户数求出样本中每户的平均用水量为660÷50=13.2t,所以估计整个小区的每户平均用水量为13.2t,最后乘以该小区总的户数即可得出该小区5月份的用水量是13.2×300=3960t.
点评:本题两次应用了样本估计总体的思想:第一次是用抽查的50户中5月份用水量不高于12t的户数占小区总户数的百分比估计出该小区300户中5月份用水量不高于12t的户数占小区总户数的百分比;第二次是用各组的中间值求出样本中每户的平均用水量来估计整个小区每户的平均用水量.
五、用样本中对应数据的比估计总体中对应数据的比
例5某学校为了了解学生上学的交通情况,选取九年级全体学生进行调查.根据调查结果,画出如图6所示的扇形统计图.图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°.已知九年级乘公交车上学的人数为50人.
(1)九年级学生中,骑自行车和乘公交车上学哪个更多?多多少人?
(2)如果全校有学生2000人,学校准备的400个自行车停车位是否足够?
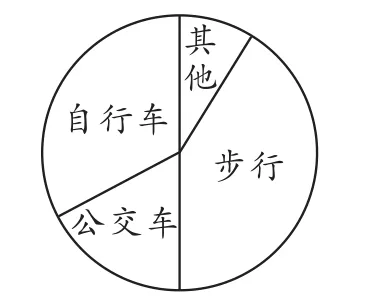
图6
解析:(1)∵120°=60°×2,
∴骑自行车的人数是乘公交车人数的2倍,
∴骑自行车的人数为50×2= 100(人),100-50=50(人).
答:骑自行车的人多,多50人.
∴学校准备400个自行车位不够.
点评:要读懂统计图,从不同的统计图中得到必要的信息.利用样本中“自行车”对应的扇形圆心角与360°的比估计总体中“自行车”对应的扇形圆心角与360°的比是解决问题的关键.
