基于电流波形检测法的开关磁阻电动机无位置传感器控制

李珍国　王红斌　王江浩　高雪飞　张纯江

(燕山大学电力电子节能与传动控制河北省重点实验室　秦皇岛　066004)

基于电流波形检测法的开关磁阻电动机无位置传感器控制

李珍国王红斌王江浩高雪飞张纯江

(燕山大学电力电子节能与传动控制河北省重点实验室秦皇岛066004)

摘要开关磁阻电动机(SRM)在采用电压PWM控制方式时，通常在定、转子齿极开始重叠位置处出现峰值电流。传统电流梯度法利用该峰值电流的前后电流微分值符号变反的特征，通过微分和过零检测电路得到转子位置，但存在检测电路参数设计繁琐，低速运行时不易获取正确的转子位置以及容错能力较差等缺点。为此，提出了一种基于电流波形检测的转子位置估算方法。该方法通过比较前后时刻电流大小，在该相关断时刻确定该相电流峰值及其对应的时间，并与前一相峰值电流对应时间共同计算确定后一相的关断时间。随后通过给定开通角，计算出开通角对应脉冲数，再通过比较当前计数值与该开通角对应的脉冲数，确定当前相或后一相的开通时间。该方法不仅保留了不依赖SRM参数的优点，而且无需微分、过零检测等外围电路，在低速运行时也能够得到正确的转子位置且具有较强的容错能力。通过基于该方法搭建的SRM无位置传感器控制系统的DSP驱动实验，证明了所提方法的可行性和有效性。

关键词：开关磁阻电动机无位置传感器控制电流波形检测法低速

0引言

开关磁阻电动机(Switched Reluctance Motor，SRM)与其他类型电动机相比，具有结构简单牢固、转矩惯性比高、调速范围宽、可靠性强、控制灵活、容错能力强、并适于恶劣环境等诸多优势[1]。但其工作需要知道转子位置信息，而该位置信息通常由安装在转轴上的物理传感器获取，这将导致SRM控制系统的成本增加且降低牢固程度。此外，在一些工作环境较恶劣或无空间安装位置传感器的场合不适合安装物理传感器。因此，能不依赖位置传感器得到转子位置，使得电动机能够稳定运行，一直受国内外学者广泛关注。

文献[2]通过事先建立的磁链和其对位置的偏导数与电流、位置的关系数据库，由激励相电压、电流积分计算得到的磁链与由磁链-电流-位置关系数据库查表得到的磁链进行比较，以该磁链偏差结合磁链偏导数-电流-位置关系数据库计算获得位置偏差，并以此实时修正转子位置，实现了SRM的高精度无位置传感器控制。文献[3-5]仅需事先建立某指定位置处的磁链-电流关系数据库，通过实时对比积分计算得到的磁链和由磁链-电流关系数据库查表得到的磁链，判断出SRM是否到达该指定位置。其中，文献[3]详细分析了所选指定位置对估算位置误差的影响，总结出该指定位置应远离非对齐和对齐位置且相电流较大的一处转子位置。文献[4]利用便于实验得到的对齐位置处的磁链-电流关系数据库，对该数据库中的磁链乘以一个小于1的系数，并与积分计算的磁链进行比较，确定是否关断激励相和开通下一相，无需再估算其他位置信息。文献[5]利用关断角位置处的磁链-电流关系数据库，与积分计算得到的磁链进行比较，确定是否到达指定关断角位置，并以此估算其他转子位置。文献[6]以忽略三次项以上的傅里叶级数电感模型为基础，推导出转子位置与激励相电感瞬时值以及傅里叶级数电感系数之间的关系表达式，并以此实时计算出转子位置。其中，激励相电感瞬时值由激励相电压、电流积分计算出的磁链除以该相电流得到；傅里叶级数电感系数由事先建立的对齐、非对齐及两者正中间位置处的电感-电流数据库查表计算得到。文献[7]利用SRM采取电压PWM控制方式时，在定、转子齿极开始重叠位置处出现峰值电流的特点，通过电流梯度法对激励相电流实时进行低通滤波—微分—二次低通滤波—过零检测，得到定、转子开始重叠位置，无需事先建立磁链或电感对位置和电流的关系数据库。文献[8-10]通过对非导通相绕组施加高频检测脉冲电压，根据响应电流斜率或峰值与瞬时电感的关系，估算出转子位置信息。其中，文献[8]给出了响应电流斜率反比于瞬时电感的关系式，根据实时计算出的响应电流斜率与给定阈值进行比较判断是否到达开通/关断角位置。文献[9]设定了两个电流阈值，分别用于判断是否到达开通/关断角位置和高频检测脉冲注入相之间的切换，以保证最大/最小电感区域不进行转子位置估计进而提高位置估计准确度。文献[11]利用SRM在电感下降区执行零电压续流时，在定、转子齿极开始不重叠位置处出现峰值电流的特点，对续流电流进行低通滤波—微分—二次低通滤波—过零检测，得到定、转子开始不重叠的位置，可采用电流滞环、电压PWM和单脉冲等控制方式。文献[12]结合基于非导通相注入高频检测脉冲的全周期电感分区策略和通过曲线拟合得到的角度-电感模型，进行了连续的转子位置估算。文献[13]为了获得连续的转子位置信息，在SRM定子齿中安装了检测线圈绕组，并对该检测线圈通入高频检测脉冲。因与相绕组互为独立，在任意转速下皆可注入高频脉冲信号，可应用于较宽调速控制场合。

与文献[7]类似，本文同样利用了当SRM执行电压PWM控制方式时，在定、转子齿极开始重叠位置处出现峰值电流的特点，但与采用电流梯度法估计峰值电流对应位置的文献[7]不同，本文提出一种新型无位置传感器控制方法：通过对激励相前后时刻采样的电流进行比较，在该相关断时刻确定该相峰值电流对应时间，并与前一相峰值电流对应时间结合计算决定后一相关断时间，而后一相开通时间由开通角任意给定。其中，时间可用固定频率的定时器计数。所提方法不仅保留了不依赖SRM参数的优点，且无需进行微分、过零检测，在低速运行时也能够得到正确的转子位置，具有较强的容错能力。通过相应的DSP驱动实验，证明了所提无位置传感器控制方法的可行性和有效性。

1理论依据

1.1电压PWM控制驱动SRM系统的相电流特点

所提出的无位置传感器控制方法以电压PWM控制方式和相电流在定、转子齿极开始重叠位置处出现峰值为前提。图1给出了SRM采取电压PWM控制方式时的理想电感、相电流和相电压波形。只要转子旋转到任意相的给定开通角和关断角(对应图1中的θon和θoff)之间时，就给该相绕组施加具有固定开关频率和一定占空比的正电压。占空比大小与转速和负载的给定有关，在系统中可由电流内环控制器得到，也可直接由速度控制器得到。当系统采用不对称桥式功率变换器和软斩波(即单管斩波)方式时，该占空比值同时是该相桥臂中负责进行PWM斩波的开关管占空比。

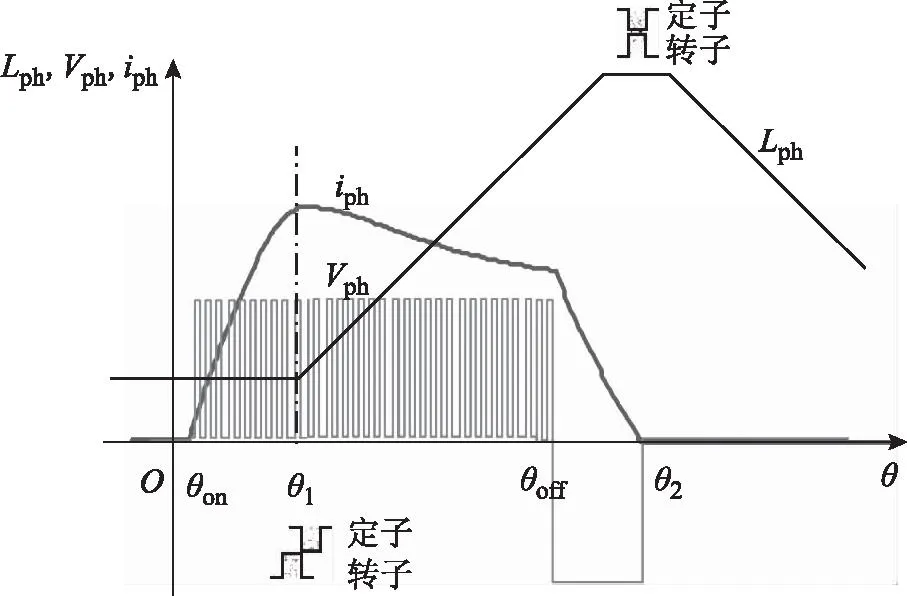
图1　电压PWM控制下的电流、电压波形Fig.1　Phase current and phase voltage waveforms in voltage PWM control

在忽略相电阻压降的条件下，基于理想电感模型，分析转子旋转到定、转子齿极开始重叠位置(即图1中的θ1)时相电流达到峰值所需条件。到达θ1的前一时刻，因电感对位置的斜率∂Lph/∂θ=0，故相电流的电流微分方程为

(1)

式中，Lmin为定、转子齿极处于非重叠位置时的电感值，即理想电感曲线中的最小值；D为PWM电压斩波所对应占空比；Udc为不对称桥式功率变换电路的直流母线电压。

由式(1)可知，转子到达θ1前，相电流将以正比于占空比的变化率持续增加，到达θ1时刻的相电流值为

(2)

式中，θon为开通角；ωrm为转子机械角速度。

经过θ1的后一时刻，相电流的电流微分方程为

(3)

式中，k为经过θ1后一时刻的电感对位置θ的斜率，即∂Lph/∂θ，在理想电感模型中k为常值。

把式(2)代入式(3)，可得

(4)

由式(4)可看出，转子到达θ1后，电流变化率的正负与θon有关，通过设定适当的θon值，可实现经过θ1后电流下降的目的，进而满足在θ1处出现峰值电流的条件。以上结论虽在忽略电阻压降且理想电感模型的条件下得到，但是仍然适用于实际运行中。

利用相电流在θ1处达到峰值的这一特点，各相可在每个电周期内能够确定一次转子位置信息，通过相邻已确定的转子位置信息除以经过时间可得转速及转子其他位置信息，从而实现换相。

1.2相电流峰值的检测

由以上分析可知，若采用某种策略检测出相电流峰值，就能够确定θ1位置。为此，文献[7]提出了一种电流梯度法：首先将相电流检测信号通过巴特沃思二阶低通滤波器滤掉PWM高频斩波信号，再经过微分电路和二次低通滤波器得到电流梯度值，最后利用过零比较器使其在转子经过θ1位置瞬间输出一个位置检测脉冲信号，从而能够确定θ1位置信息。该方法因无需事先知道电动机的电阻、电感或磁化曲线等参数，具有不依赖SRM参数的优点，但是也存在如下缺点：

(1)考虑到微分运算和非线性电流波形，使得电流梯度检测电路的参数设计较为繁琐。

(2)在低速运行时，因单位时间内的电流变化很小，微分计算准确度会大大降低，得不到正确的转子位置。

经尾静脉注射肿瘤细胞后，小鼠体质稳定，状态良好。4%多聚甲醛固定48 h后肝组织的大体标本，于体视显微镜下观察，发现对照组的肝组织有少量的转移灶，实验组和预防组未发现肉眼可见的转移灶；对照组可见微小转移灶，在实验组和预防组未见明显的微小转移灶。

(3)当电流梯度检测电路错误地输出一个位置检测脉冲信号时无法做到其他补救措施，即容错能力较差。

针对以上缺点，本文采用通过比较前后时刻电流大小获得电流峰值，以达到无须进行微分、过零比较检测，低速时也能正确得到转子位置的目的。此外，为提高容错能力，在激励相关断时刻确定电流峰值,并以此确定转子位置信息，不会在经过θ1位置瞬间确定。

图2给出了通过比较前后时刻值获取电流峰值的示意图。

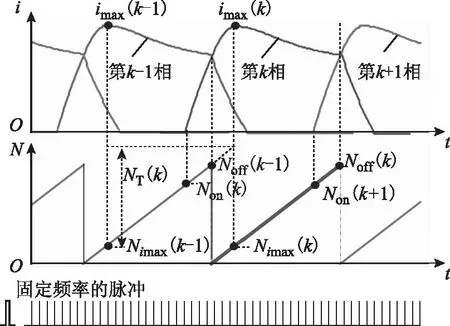
图2　通过比较前后时刻值获取电流峰值的示意图Fig.2　Principle diagram of peak current by comparing the value before and after

图2中，采用固定频率的脉冲数计时，当前相即第k相的计时从前一相即第k-1相的关断时刻开始，持续到当前相的关断时刻结束。在此计数过程中，通过不断地比较前后时刻采样电流大小，获得并保存相电流峰值imax(k)和对应脉冲数Nimax(k)。如此，可在当前相关断时刻，利用Nimax(k)和前一相的Nimax(k-1)，计算得到经过相邻两相间电流峰值之间距离对应脉冲数NT(k)。

NT(k)=Nimax(k)+Noff(k-1)-Nimax(k-1)

(5)

式中，Noff(k-1)为前一相关断角对应脉冲数。

对于已有SRM，该相邻两相间电流峰值之间距离为常数，如对于三相12/8 SRM，该距离为15°。

1.3开通、关断时刻的确定

当前相关断时刻由当前相计数过程中通过比较当前计数值N(k)与关断角对应脉冲数Noff(k)确定。而Noff(k)是在前一相关断时刻由前次的NT(k-1)计算得到。由图2可知，理想情况下有Noff(k)=NT(k-1)。但由于使用脉冲计数并且存在电流检测、计算、积累等误差，使得须对NT(k-1)进行一定修正后才会等于Noff(k)，如图3所示。其计算公式为

Noff(k)=NT(k-1)+NΔ(k-1)-N2(k-1)

(6)

式中，N2(k-1)为前一相电流峰值所在位置到该相实际关断位置之间的脉冲数，N2(k-1)=Noff(k-1)-Nimax(k-1)；NΔ(k-1)为前一相电流峰值所在位置到该相理想关断位置之间的脉冲数，NΔ(k-1)=GoffNT(k-1)；Goff为电流峰值所在位置到该相理想关断角位置之间的距离与相邻两相开通角或关断角之间的距离之比。对于已有SRM，当给定关断角θoff固定不变时，Goff为常数。

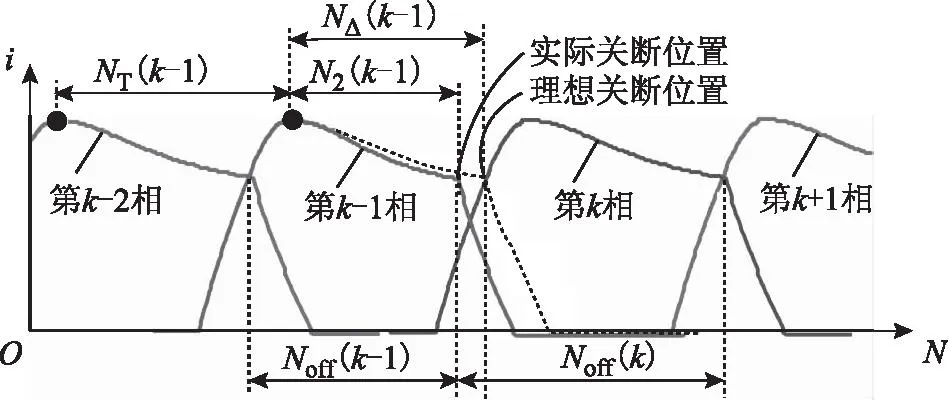
图3　确定当前相关断时刻对应脉冲数的示意图Fig.3　Principle diagram of confirming the pulse count of turn-off moment at present

由此可得Noff(k)的最终计算公式为

Noff(k)=(1+Goff)NT(k-1)+Nimax(k-1)-Noff(k-1)

(7)

当导通角(即θdw=θoff-θon)大于相邻两相开通角或关断角之间的角度时，后一相的开通时刻会出现在当前相的关断时刻之前，如图4中的第k+1相开通时刻出现在第k相关断时刻之前。此时，在当前相计数过程中，通过比较当前计数值N(k)与开通角对应脉冲数Non(k+1)，可确定后一相的开通时刻。由图4可知，Non(k+1)的计算公式为

Non(k+1)=Noff(k)-GonNT(k-1)

(8)

式中，Gon为后一相开通到当前相理想关断角之间的距离与相邻两相开通角或关断角之间的距离之比，Gon仅与开通角θon有关。

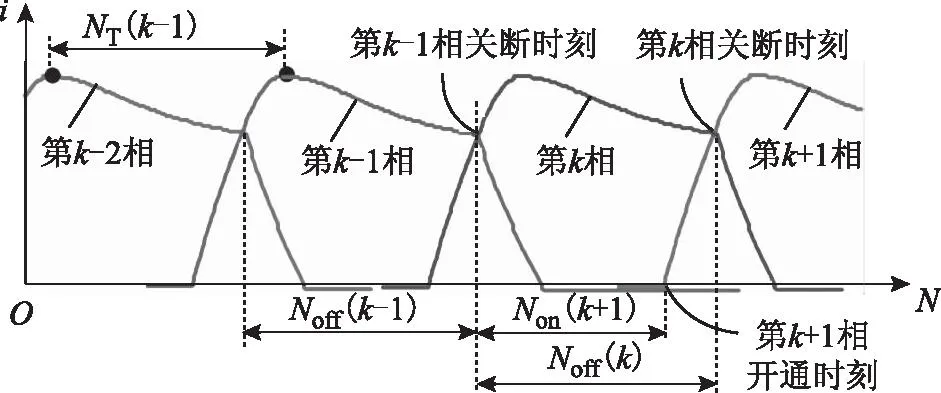
图4　确定后一相开通时刻对应脉冲数的示意图Fig.4　Principle diagram of confirming the pulse count of turn-on moment at the next phase

同理，当导通角不大于相邻两相开通角或关断角之间的角度时，后一相的开通时刻会出现在当前相的关断时刻之后。因与前段分析类似，在此不再赘述。

1.4系统的整体构成

基于上述无位置传感器控制方法，搭建了如图5所示的SRM速度控制系统。系统中，电压PWM控制器所需占空比D*由速度控制器直接给出；各相的开通/关断信号由开通/关断时刻输出单元，比较当前的脉冲计数值N(k)与计算得到的开通/关断角对应脉冲数确定。图5中，以前一相关断时刻为例，给出了当前相关断角对应脉冲数Noff(k)和后一相开通角对应脉冲数Non(k+1)的获取框图，分别对应式(7)和式(8)。此外，图5中还以当前相开始计数到该相关断前为例，给出了当前相电流峰值对应脉冲数Nimax(k)和相邻两相电流峰值之间对应脉冲数NT(k)的获取框图，对应式(5)，且由NT(k)通过转速计算单元得到转速信息，以便用于转速闭环控制。

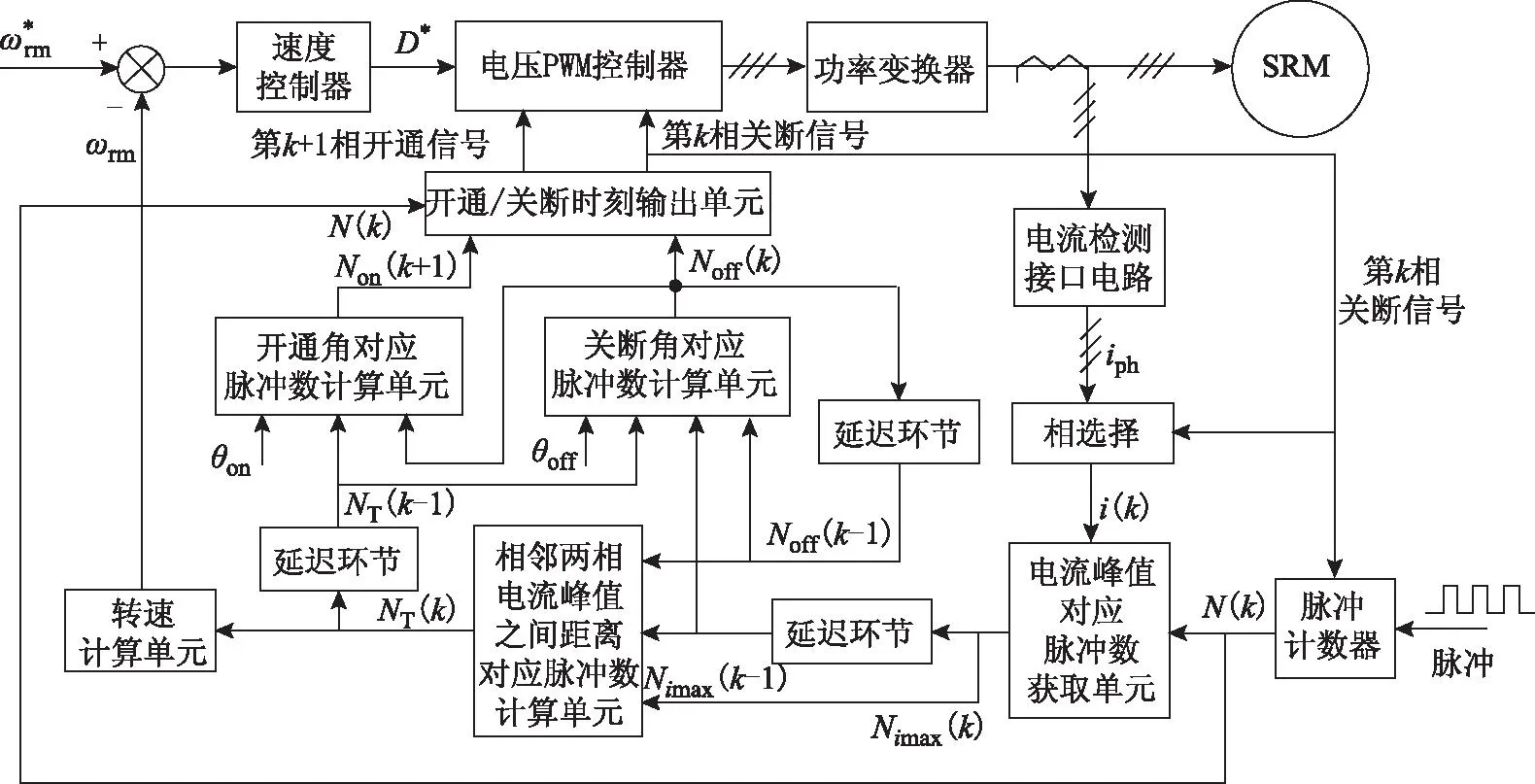
图5　所提开关磁阻电动机无位置传感器控制系统Fig.5　Proposed SRM sensorless control system

2系统实验

2.1电动机主要参数

为了验证所提无位置传感器控制方法的有效性，把一台三相12/8极SRM用作实验样机。电动机的额定电压、额定转速和额定功率分别为300 V、1 800 r/min 和130 W；定、转子极宽分别为14°和16°。图6给出了SRM无位置传感器控制实验系统。实验中使用的DSP采用TI公司的TMS320F28335—150，用于计时的脉冲计数器的频率为40 kHz。直流母线电压为300 V，负载采用Magtrol公司的磁滞测功机(HD—705—8NA—0100型)，可由同一家公司的DSP6001型控制器提供独立于转速的制动转矩。

图6　无位置传感器控制实验系统Fig.6　Sensorless control experimental system

2.2所提方法的可行性验证

由上述分析可知，所提无位置传感器控制方法是否可行，与相电流峰值的捕获和关断角对应脉冲数的估算密不可分。为此，控制系统在有位置传感器下采用电压PWM控制方式运行时，分别进行了获取电流峰值对应位置并以此计算关断角对应脉冲数的实验。

图7给出了560 r/min的转速下，获取电流峰值对应位置的实验结果。转子的参考位置固定在A相的定、转子齿极对齐位置。实验中，A相每次开通起至关断，实时进行前后时刻电流的比较，在A相关断时刻确定电流峰值，并把该值imax与其对应转子位置θimax保存到DSP中。图7中θ即为A相工作期间实时得到的电流峰值对应转子位置波形。实验结果表明，虽然每次检测到的电流峰值对应位置与实际值之间有一定的偏差，但是其偏差不大。如在图7中，电流峰值大都发生在29.3°的位置处，其上下偏差小于0.7°。改变转速和负载也会得到近似结果。

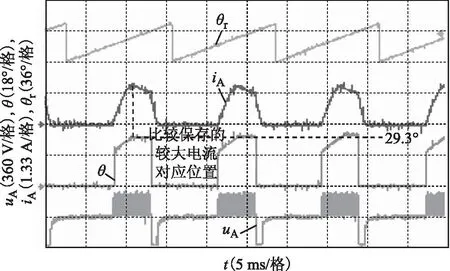
图7　获取电流峰值对应位置的实验结果Fig.7　Experimental results for obtaining the position of peak current

图8分别给出了210 r/min和1 000 r/min的转速下，计算关断角对应脉冲数Noff的实验结果。实验中，一旦当前相的计数值N(k)超过Noff(k)时，当前相的计数立即结束，并开始后一相的计数且计数器值N(k+1)清零。同时，在这一时刻利用已存的电流峰值对应脉冲数Nimax(k)，代入式(5)计算得到过去两相电流峰值之间对应脉冲数NT(k)；再通过式(7)计算得到后一相的Noff(k+1)。实验结果表明，通过计数值与关断角对应脉冲数比较而获得的关断时刻和位置都很接近所希望的关断时刻和位置，可完全替代给定关断角与实际转子位置的比较。由于用于计时的脉冲计数器的频率是固定的，因此随着转速增加，关断角对应脉冲数Noff将减小，使得电流峰值检测准确度对关断时刻和位置的影响会增加。

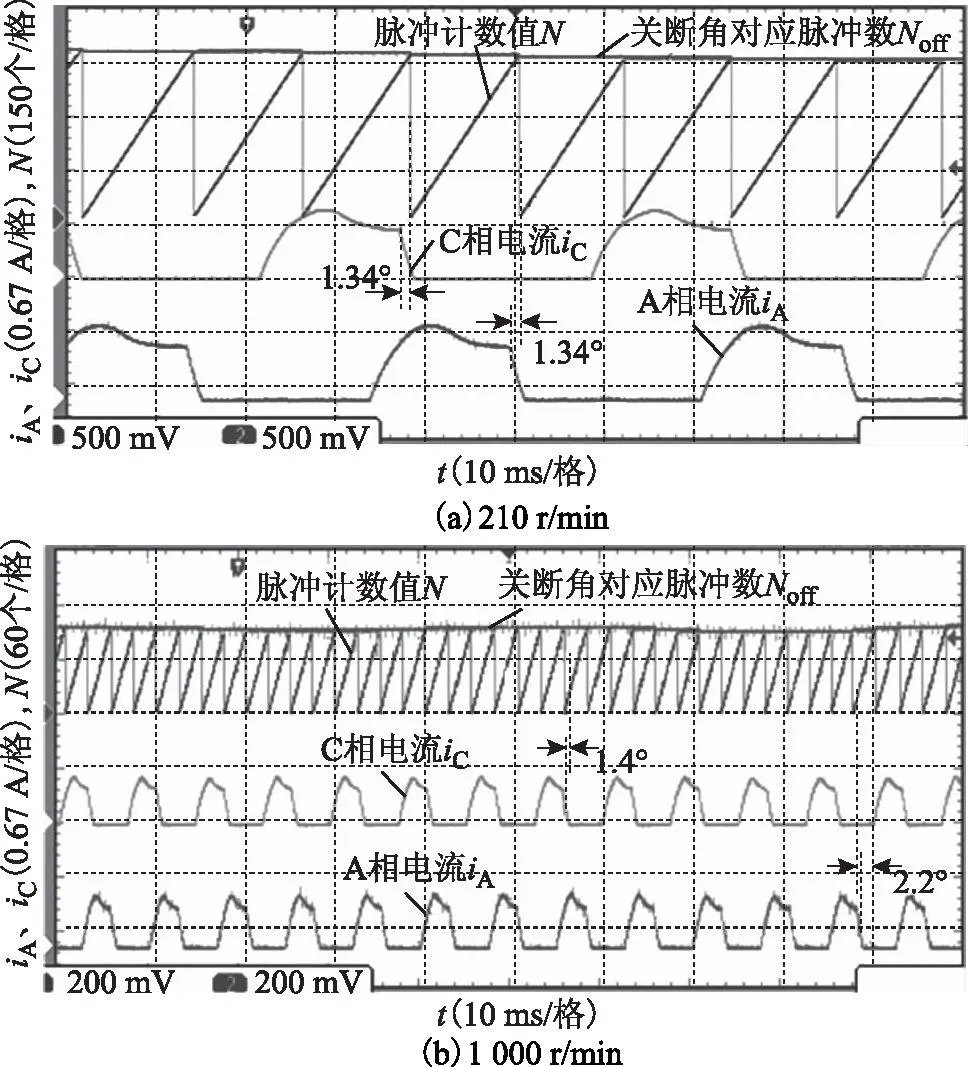
图8　计算关断角对应脉冲数的实验结果Fig.8　Experimental results of counting the pulse count of turn-off angle

2.3所提无位置传感器控制系统

图9分别给出了240 r/min和600 r/min的转速下，基于所提无位置传感器控制方法确定开通/关断时刻时的稳定运行实验结果。图9中，为便于比较，同时给出了按实际转子位置和同频率计数的波形。当通过位置传感器检测到转子到达各相指定关断角位置时，该计数值将清零并重新计数。实验中，开通/关断角分别定为20.3°和39.4°。考虑到电流峰值基本出现在29.3°，式(7)和式(8)中的Goff和Gon分别为0.673和0.273。实验结果表明，以计数值与开通/关断角对应脉冲数比较而选择开通/关断时刻时，其关断位置很接近以实际转子位置确定的关断角位置，能够保证电动机运行平稳。而且，在当前相关断位置处，通过相邻的电流峰值对应脉冲数，能够判断所得当前相的Nimax(k)是否可用。若某种理由导致得到的Nimax(k)与前一相的Nimax(k-1)比较差异较大，则可舍弃当前相的Nimax(k)，以前一相的Nimax(k-1)取代它。这种措施虽然可提高无位置控制方法的容错能力，但也将带来不适用于转速变化较大场合的缺点。

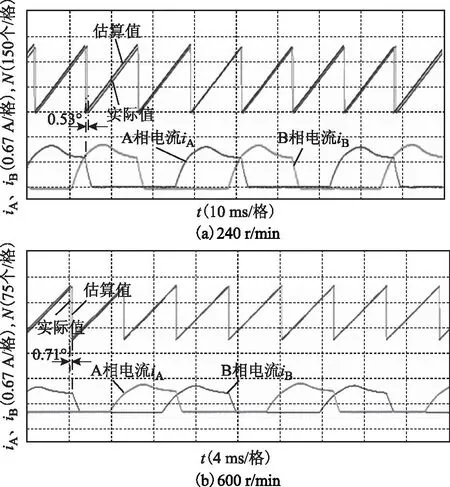
图9　无位置传感器条件下稳定运行时的实验结果Fig.9　Experimental results of stable operation after sensorless control system

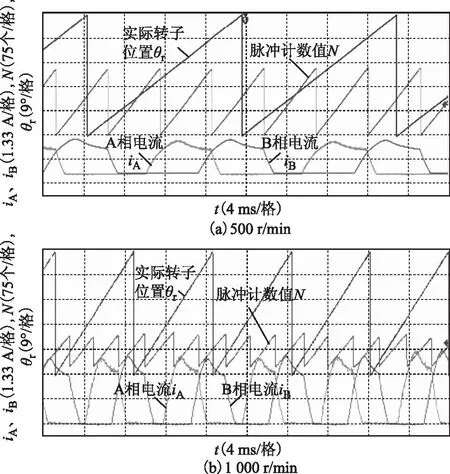
图10　额定负载下的无位置传感器控制实验结果Fig.10　Experimental results of sensorless control at rated load

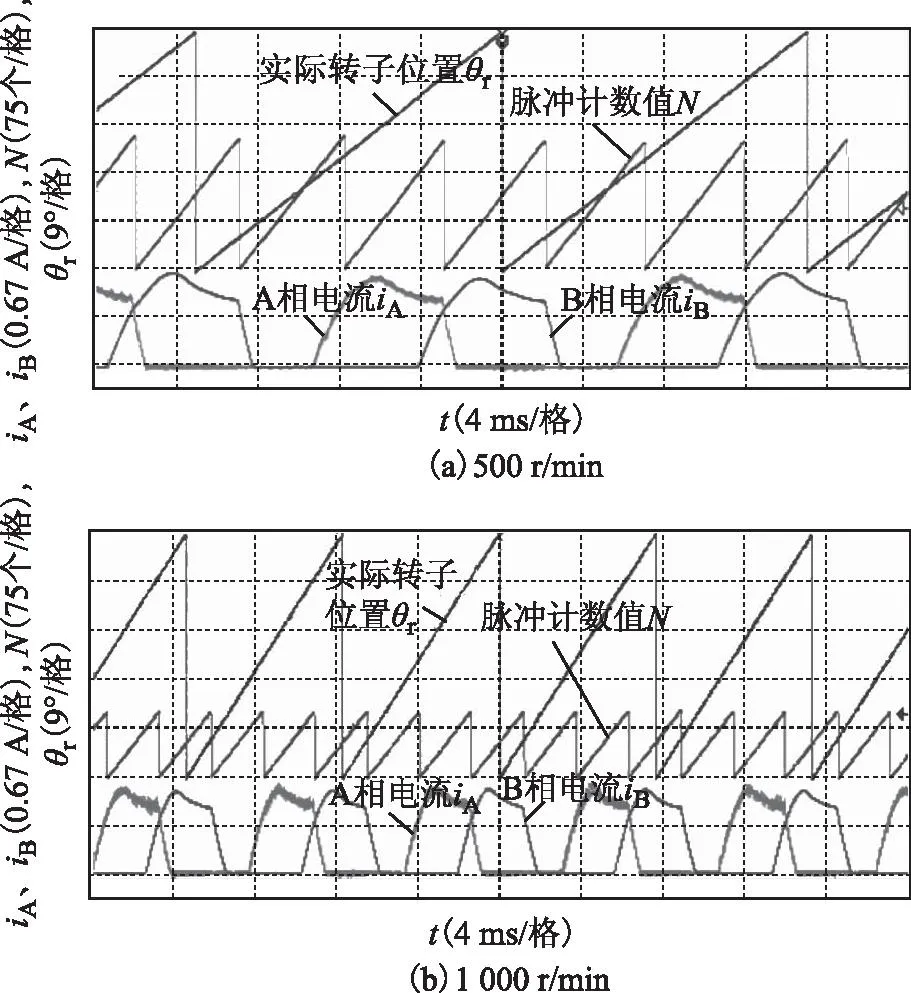
图11　1/2额定负载下的无位置传感器控制实验结果Fig.11　Experimental results of sensorless control at half rated load

图10和图11分别给出了在额定转矩(0.7 N·m)和1/2额定转矩(0.35 N·m)负载下的电动机无位置传感器控制实验结果。图中，为了得到各相实际开通和关断位置，同时给出了由位置传感器检测到的实际转子位置波形。实验结果表明，无论是额定负载或1/2额定负载，还是500 r/min或1 000 r/min，当采用所提无位置传感器控制方法时，各相的实际开通/关断角都很接近给定值，偏差小于0.7°，能够保证电动机稳定运行。

图12给出了额定负载下，电动机在500 r/min的转速稳定运行时，以斜坡方式给定1 000 r/min，待转速稳定后再以斜坡方式给定500 r/min时的无位置传感器速度控制系统实验结果。所提无位置传感器控制方法由于不适用于转速变化较大的场合，在此给定以某一固定斜率变化的斜坡参考转速。实验中，每15°计算一次转速并执行PI速度控制器。从实验结果可看出，基于所提无位置传感器控制方法的PI调速系统，工作稳定，调速性能良好。

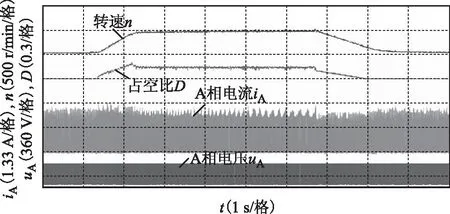
图12　斜坡转速指令下的无位置传感器控制实验结果(500→1 000→500 r/min)Fig.12　Experimental results of sensorless control at ramp speed reference

3结论

本文提出了一种开关磁阻电动机无位置传感器控制新方法，对该方法的理论分析与实验结果表明：

1)通过比较前后时刻电流大小，可获取该电流峰值和其对应时刻，无须进行微分、过零比较检测。计时间可用固定频率的脉冲计数器，起、终点分别是前一相和当前相的关断时刻。

2)通过给定关断角，可计算出关断角对应脉冲数。根据当前计数值与该关断角对应脉冲数的比较，确定当前相的关断时刻。

3)通过给定开通角，可计算出开通角对应脉冲数。根据当前计数值与该开通角对应脉冲数的比较，确定当前相或后一相的开通时刻。

4)所提无位置传感器控制方法与电流梯度法一样，同样不能适用于起动。因此需要配套其他起动方法使用。

5)由于在导通相关断时刻才确定电流峰值和对应脉冲计数值，通过前一相和当前相的相关脉冲数的比较，可判断检测到的电流峰值与对应脉冲数是否可用，故会增强无位置传感器控制系统的容错能力，但会带来该方法不适用于转速变化较大场合的缺点。

6)该方法无需外接额外硬件，无需存磁化曲线数据，控制器所占空间和运算量较小。

参考文献

[1]Krishnan R.Switched reluctance motor drive：modeling，simulation，analysis，design and application[M].Boca Raton FL，USA：CRC Press，2001.

[2]Lopez G，Kjaer P C，Miller T J E.High-grade position estimation for SRM drives using flux linkage/current correction model[J].IEEE Transactions on Industry Applications，1999，35(4)：859-869.

[3]Lyons J P，MacMinn S R，Preston M A.Flux/current methods for SRM rotor position estimation[C]//IEEE Industry Application Society Meeting，Dearborn，MI，1991，1：482-487.

[4]邱亦慧，詹琼华，马志源，等.基于简化磁链法的开关磁阻电机间接位置检测[J].中国电机工程学报，2001，21(10)：59-62.

Qiu Yihui，Zhan Qionghua，Ma Zhiyuan，et al.The indirect position sensing of SRM on the basis of simplified flux method[J].Proceedings of the CSEE，2001，21(10)：59-62.

[5]李珍国，李彩红，阚志忠，等.基于改进型简化磁链法的开关磁阻电机无位置传感器速度控制[J].电工技术学报，2011，26(6)：62-66.

Li Zhenguo，Li Caihong，Kan Zhizhong，et al.Switched reluctance motor sensorless speed control based on the improved simplified flux method[J].Transactions of China Electrotechnical Society，2011，26(6)：62-66.

[6]蒯松岩，王鹏飞，成静红，等.基于变系数电感模型开关磁阻电机四象限无位置传感器技术[J].电工技术学报，2014，29(7)：114-124.

Kuai Songyan，Wang Pengfei，Cheng Jinghong，et al.Four-quadrant position sensorless technology of switched reluctance motors based on variable coefficients inductance model[J].Transactions of China Electrotechnical Society，2014，29(7)：114-124.

[7]Gallegos-Lopez G，Kjaer P C，Miller T J E，et al.A new sensorless method for switched reluctance motor drives[J].IEEE Transactions on Industry Applications，1998，34(4)：832-840.

[8]Yu C H，Chen T C.Novel sensorless driving method of SRM with external rotor using impressed voltage pulse[J].IEEE Proceedings on Electric Power Applications，2006，153(5)：632-641.

[9]张磊，刘闯，王云林，等.开关磁阻电机变双电流阈值的无位置传感器技术[J].中国电机工程学报，2014，34(27)：4683-4690.

Zhang Lei，Liu Chuang，Wang Yunlin，et al.Position sensorless technology of switched reluctance machines based on double variable current thresholds[J].Proceedings of the CSEE，2014，34(27)：4683-4690.

[10]邵杰，邓智泉，胡荣光，等.基于改进脉冲注入开关磁阻电机无位置传感器技术[J].电工技术学报，2015，30(21)：147-153.

Shao Jie，Deng Zhiquan，Hu Rongguang，et al.An improved sensorless driving method of switched reluctance motors using impressed voltage pulse[J].Transactions of China Electrotechnical Society，2015，30(21)：147-153.

[11]曾辉，陈昊，徐阳.基于分步续流法的开关磁阻电机无位置传感器控制[J].电工技术学报，2013，28(7)：124-130.

Zeng Hui，Chen Hao，Xu Yang.Sensorless control of switched reluctance motor based on fractional step freewheeling methods[J].Transactions of China Electrotechnical Society，2013，28(7)：124-130.

[12]蔡骏,邓智泉.基于全周期电感法的开关磁阻电机无位置传感器控制技术[J].电工技术学报,2013,28(2):145-154.

Cai Jun,Deng Zhiquan.Sensorless control of switched reluctance motors based on full-cycle inductance method[J].Transactions of China Electrotechnical Society，2013,28(2):145-154.

[13]王骋,邓智泉,蔡骏,等.利用检测线圈的开关磁阻电机转子位置估计方法[J].电工技术学报,2015,30(14):41-50.

Wang Cheng，Deng Zhiquan，Cai Jun，et al.Rotor position estimation for switched reluctance motor with searching coils[J].Transactions of China Electrotechnical Society,2015,30(14):41-50.

Sensorless Control of Switched Reluctance Motor Based onCurrent Waveform Detection Method

Li ZhenguoWang HongbinWang JianghaoGao XuefeiZhang Chunjiang

(Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province Yanshan UniversityQinhuangdao066004China)

AbstractIn case of switched reluctance motor(SRM)using voltage PWM control mode,the peak current usually appears at the initial overlapping position between the stator and the rotor poles.In the conventional current gradient method,the rotor position can be estimated through the differential and zero crossing detection circuit by using the characteristics of the sign inversion of the current differential value before and after the peak current.However this method has such disadvantages as tedious parameters design for differential and zero crossing detection circuit,difficulty in obtaining the correct rotor position under the low-speed region,and poor fault tolerance ability.For these reasons,a current waveform detection based rotor position estimation method is proposed in this paper.This method confirms the phase peak current and the corresponding time in the turn-off time by comparing the current values before and after the present moment,then calculates and confirms the turn-off time of the next phase by combining the time of the previous phase peak current.Then the pulse number which corresponds to the opening angle can be calculated by given the opening angle,and then the turn-on time of the present or the next phase can be confirmed by comparing the present count value with the pulse number which corresponded to the opening angle.Compared to conventional current gradient method,the proposed method not only retains the merit of conventional method,such as independent of SRM parameters,but also needs no differential and zero crossing detection peripheral circuits.Meanwhile,the proposed method could get more correct rotor position and have better fault tolerant ability at low speed region.Through DSP based experiments on the SRM sensorless control system which is constructed according to the proposed method,the feasibility and validity of the proposed method is verified.

Keywords：Switched reluctance motor，sensorless control，current waveform detection method，low speed

收稿日期2015-09-21改稿日期2015-12-22

作者简介E-mail：lzg@ysu.edu.cn E-mail：zhangcj@ysu.edu.cn(通信作者)

中图分类号：TM352

国家自然科学基金资助项目(51477148)。

李珍国男，1973年生，博士，副教授，研究方向为电力电子与电力传动。

张纯江男，1961年生，研究方向为电力电子与电力传动。