大数据背景下贝叶斯模型平均的理论突破与应用前景
2016-06-29刘乐平卢志义
高 磊,刘乐平,卢志义
(1.天津财经大学 大数据统计分析中心, 天津 300222; 2.天津商业大学 理学院, 天津 300134)
大数据背景下贝叶斯模型平均的理论突破与应用前景
高磊1,刘乐平1,卢志义2
(1.天津财经大学 大数据统计分析中心, 天津 300222; 2.天津商业大学 理学院, 天津 300134)
摘要:大数据统计分析过程中常面临模型比较和选择的不确定性问题。贝叶斯模型平均(BMA)方法可以通过先验和后验概率度量模型不确定性,并利用后验概率对模型的结果进行加权平均,最终得到更稳健的估计结果。在回顾贝叶斯模型平均发展历程的基础上,介绍贝叶斯模型平均的基本原理,综述其在一些难点问题上的理论进展,并介绍大数据背景下贝叶斯模型平均的应用前景。贝叶斯模型平均与复杂数据分析方法相结合,可能成为大数据研究的新思路。
关键词:大数据;模型不确定性;贝叶斯模型平均;MCMC
一、引言
在大数据的统计实践中,研究人员常常构建一组模型,然后依据模型选择准则,从中挑选 “最优”模型进行统计推断和预测。这里就有两个值得考虑的问题:第一,单从模型选择准则来分析,可能会得到几个模型对数据拟合均较好的结论。也就是说,这些模型难分伯仲,舍弃其中任何一个都令人可惜,Breiman就把这种现象称为模型选择的“罗生门效应”*《罗生门》是一部日本电影,在电影中发生了一起刑事案件,一名男性被杀,另有一名女性被强奸。案件共有四名目击者,当他们在法庭作证时,面对同样的事件,却从自身利益出发讲述了完全不同的事情经过。Brieman认为统计模型也具有“罗生门效应”,即不同模型讲述了关于同一数据的不一样的故事,而且听起来都非常逼真。(Rashomon Effect)[1];第二,即便可以选出最优模型,由于数据样本的随机性,每次选择的最优模型也可能有所不同,这就是所谓的模型不确定性(Model Uncertainty)[2]。在统计分析中,这两个问题较为普遍,但经常被研究人员所忽略。
贝叶斯模型平均(Bayesian Model Averaging, BMA)方法以贝叶斯理论为基础,将备选模型作为随机变量,通过赋予先验概率和后验概率来度量其不确定性,并利用后验概率对备选模型的结果进行加权平均,最终得到更稳健的估计结果。不妨做一比喻,如果单个模型的结果是含有金子的渣块,那么研究人员应像淘金者,与其选择含金量最大的渣块,不如利用一种方法从所有的渣块中淘取更多的金子。BMA就是一种从多个模型中“淘金”的方法,即把各模型的结果综合起来,发挥各模型的优势,并融合更多的信息。
BMA方法改变了人们对模型比较和模型选择的传统认识,是对经典建模理论的有益补充。30多年来,随着计算技术的不断进步,特别是MCMC(Markov Chain Monte Carlo)方法的发展,BMA方法渐趋成熟,其应用也愈加广泛。笔者在回顾BMA方法发展历程的基础上,介绍BMA方法的基本原理,并综述大数据背景下贝叶斯模型平均的理论突破,介绍BMA的一些应用。
二、贝叶斯模型平均的发展历程
模型平均起源于20世纪60年代,而BMA是模型平均方法的一个重要分支*模型平均方法另一个重要分支是频率模型平均(Frequentist Model Averaging, FMA)。。1963年,Barnard在研究民用航空数据时首次提出模型综合的概念。1965年,Roberts考虑了一种结合两名专家观点的预测分布,该分布本质是两个模型后验分布的加权平均。1969年,Bates和Granger通过综合两个无偏预测来预测航空需求,肯定了模型综合方法在统计预测中的优势,他们的论文催生了20世纪70年代关于模型综合的研究。1978年,Leamer进一步完善了模型综合方法,首次提出了BMA分析的基本范式,Leamer认为BMA方法就是从概率的角度度量模型的不确定性。继Leamer之后,BMA的研究沉寂了一段时期。
20世纪80年代末90年代初,MCMC方法的发展极大地促进了现代贝叶斯统计学的复兴[3],与此同时,忽视模型不确定性所带来的弊端也再次引发了学者的思考。在这种背景下,George、Drapper、Raftery等学者重新开展了BMA方法的研究,BMA迎来了理论发展的黄金时期。在10多年的时间里,学者们针对设定先验分布、计算边际似然和模型搜索等难点问题进行了深入研究,并取得一系列理论进展(见本文第三部分)。1999年,Hoeting等人在国际著名统计期刊《StatisticalScience》上发表了综述文章[4],全面回顾90年代 BMA方法的理论进展,并对21世纪BMA的应用前景进行展望,这篇文章标志着BMA方法渐趋成熟,目前该文引用已达2 727次*截至2016年1月1日。。
进入21世纪,BMA在国内外得到了迅猛的发展和应用。2005年,Gneiting和Raftery合作在世界顶级学术刊物《Science》的气象科学板块撰文,指出利用贝叶斯模型平均方法进行天气预测更为有效[5]。除气象学研究外,在大数据背景下,BMA方法的应用领域还包括计量经济学、医学健康、水文地理、工程技术等(见本文第四部分)。
三、大数据背景下贝叶斯模型平均的理论突破
(一)BMA的基本原理
贝叶斯模型平均是一种从多个模型中“淘金”的方法。若Δ是所感兴趣的“金子”(Δ可能是系数的估计,也可能是未来的预测),那么在观测数据D给定的条件下,通过BMA方法得到的后验分布是:
(1)
其中M1,M2,…,MK表示备选模型,p(Mk|D)表示备选模型Mk的后验概率,而p(Δ|Mk,D)表示在备选模型Mk下Δ的后验分布。因此,由BMA所得的后验分布p(Δ|D)是各备选模型下后验分布p(Δ|Mk,D)的加权平均,加权权重为各备选模型的后验概率。
根据Δ后验分布式(1),可得后验均值和方差:
(2)
Var[Δ|D]
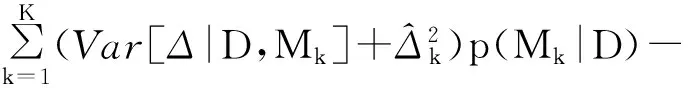
E[Δ|D]2
(3)

研究表明,由BMA得到的均值预测式(2)会优于单个模型预测。一个直观的解释是,若各模型的预测结果均是无偏的,那么选择单个模型的预测结果就如同从多个无偏预测中随机抽取一个预测值,虽然结果无偏,但其方差的不确定性仍然很大;而利用合适的权重对各模型的预测值加权平均,不仅仍然可以得到无偏估计,还可以降低估计的方差,从而提高估计的准确性。可证明,在对数得分标准下,由BMA得到的的预测不仅优于单个模型的预测,而且比其他加权平均结果要好。
备选模型的后验概率p(Mk|D)非常重要,在式(1)、式(2)、式(3)中均有出现,表示对备选模型的“信赖”程度。备选模型的后验概率可根据贝叶斯公式得到:
(4)
其中p(Mk)是备选模型Mk的先验概率,p(D|Mk)是在备选模型Mk下观测数据D的边际似然,即:
p(D|Mk)=∫p(D|θk,Mk)p(θk|Mk)dθk
(5)
其中θk表示模型Mk中的参数向量,p(θk|Mk)表示模型Mk中参数θk的先验分布,而p(D|θk,Mk)则表示在给定模型Mk和参数θk下,观测数据D的似然。式(5)涉及积分运算,因此边际似然又被称为积分似然。
式(1)~式(5)含义清楚易于理解,涵盖了BMA的基本方面,但在BMA的应用中,仍有不少细节需要考虑,某些细节至关重要已然成为BMA的应用难点。从20世纪90年代至今,学者们围绕这些难点问题进行了深入研究并取得了一系列理论进展。按照BMA分析的流程,这些难点可归纳为以下三个方面:
1.设定先验分布。应用BMA时,首先需要设定参数和模型的先验分布。参数先验分布出现在计算模型边际似然的式(5)中,边际似然是计算模型后验概率的关键,而模型的先验概率也会影响模型后验概率。因此,如果选择了不稳健的先验分布,不仅会得到失真的模型后验概率,而且还会降低BMA的预测能力。
2.求解边际似然。边际似然直接影响模型后验概率。与似然函数不同,边际似然是似然函数在参数先验分布下的期望,涉及积分运算。积分运算常常较为复杂,尤其当模型的参数维度较多时,一般积分算法难以处理这种高维积分问题。不过,在贝叶斯线性回归模型中,通过把参数设置为共轭先验,也可得到边际似然解的解析形式,但共轭先验只是先验分布的一种特殊情形,在更为复杂的贝叶斯模型中,如果根据需要将参数设定为非共轭先验,那么积分运算仍然会非常困难。求解边际似然是BMA应用中必须克服的一个难点。
3.搜索模型空间。利用边际似然求解的近似或模拟方法,可以得到单个模型的边际似然,但当备选模型的数量巨大时,要求出所有模型的边际似然乃至后验概率,在计算上是不可能完成的。例如陈伟等人在利用贝叶斯模型平均方法预测中国通货膨胀率时,考虑了28个解释变量,在单一模型为线性模型假设下,备选模型总数多达268 435 456个[6]*线性回归模型中,每个解释变量都有两种选择:进入模型或在模型外,因此若有5个解释变量,则模型空间中共有25=32个备选模型;若有20个解释变量,则模型空间中共有220=268 435 456个备选模型,可见备选模型的数量随解释变量个数增加呈指数式增长。。实际上,当解释变量个数超过20个时就不能像式(1)那样对所有模型加权平均,而如何设计一种模型搜索策略,在模型空间中进行搜索、得到模型空间的一个子集、然后在这个子集基础上进行BMA,则是学者关注的又一个难点问题。
(二)设定参数先验分布
回归模型是BMA方法讨论最为成熟的模型。首先介绍回归模型中常用的先验形式——Zellner’sg先验,然后介绍另外两种设定参数先验的方法。
1.Zellner’sg先验。设被解释变量为Y,解释变量为X1,X2,…,Xp。完整的回归模型应包括p个解释变量,而其他备选模型则考虑p个解释变量的一个子集,用Xk表示X1,X2,…,Xp的子集,则备选模型Mk可表示为:
Mk:Y=Xkβk+ε
(6)
其中 Xk为设计矩阵,βk为相应的回归系数,ε为误差向量,一般假设ε~Nn(0,σ2I)。

(7)
然后将方差σ2设定为无信息先验分布:
(8)
式(7)和式(8)构成回归模型的Zellner’sg先验。在Zellner’sg先验中,一般令β0=0,因此Zellner’sg先验只需指定超参数g即可。在Zellner’sg先验假设下,βk和σ2的联合后验密度可以分解为:
p(βk,σ2|D)∝p(βk|D,σ2)p(σ2|D)
(9)
这里分解的两项p(βk|D,σ2)和p(σ2|D)均是常见的分布形式,其中p(βk|D,σ2)是多元正态分布,p(σ2|D)是逆伽马分布。
Zellner’sg先验由Zellner(1986)提出且应用较为广泛,在BMA方法中使用Zellner’sg先验的好处是明显的:首先,Zellner’sg先验形式简洁,只需设定一个参数,而且参数的后验分布是常见的分布形式;其次,在Zellner’sg先验假设下,备选模型对空模型(不含解释变量,仅有截距项)的贝叶斯因子容易求出,因此方便进行模型比较;此外,在马尔科夫链蒙特卡洛模型综合(Markov Chain Monte Carlo Model Composition,MC3)等模型搜索算法中,Zellner’sg先验可以提高算法计算效率。
2.数据依赖先验(data-dependent prior)。参数先验是进行数据分析之前关于参数的信息,与观测数据联系很少,因此“数据依赖先验”的概念可能令人疑惑。然而,当研究人员关于参数的先验信息极少时,将先验分布设定为数据依赖先验仍是可行的。Wasserman证明,数据依赖先验不仅具有良好的性质,而且比采用数据独立先验(data-independent prior)有更好的预测能力。此外,由于考虑了数据信息,数据依赖先验比无信息先验更为稳健。
3.单位信息先验(Unit Information Prior,UIP)。Kass和Wasserman提出的单位信息先验的概念为多元正态分布,其均值为参数极大似然估计,协方差矩阵是由一单位观测数据得到的Fisher信息的逆矩阵。用一个例子描述其基本思想,假设观测数据的分布是正态分布,即:
Yi~N(ψ,σ2)(i=1,2,…,n)
(10)
这里σ已知;ψ未知,是待估参数,那么ψ的单位信息先验可设定为:
ψ~N(ψ0,τ2)
(11)
其中ψ0为观测数据Y1,Y2,…,Yn的样本均值,而τ=σ,这表示式(11)包含的关于ψ的信息(由τ2度量),与一单位观测数据包含的关于ψ的信息(由σ2度量)是相同的,这正是单位信息先验名称的由来。由该先验得到的贝叶斯因子与施瓦茨准则结果接近,但也面临与施瓦茨准则相同的问题,即其模型选择结果比较保守,偏向于较为简单的模型。
(三)设定模型先验概率
Raftery提出模型的均匀先验,即为所有模型指定相同的先验概率:
(12)
其中K是模型空间中备选模型的总数。模型均匀先验表示对所有备选模型都一视同仁,不偏向也不歧视任何备选模型。在均匀先验下,模型后验概率可以进一步简化:
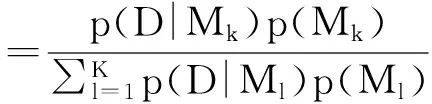
(13)
可见,由于各模型先验概率相同,分子分母中先验概率一项可以消去,模型后验概率不受模型先验的影响,只由模型的边际似然决定。在BMA应用研究中,设定模型均匀先验较为流行,这是因为从形式上看式(12)简洁、方便,从应用上看这种方式也符合直觉,容易被数据分析客户接受。
Mitchell和Beauchamp提出,在回归模型中从解释变量的角度设置模型先验:
(14)
其中δkj为指示变量,δkj=1表示解释变量Xj进入回归模型Mk中,δkj=0表示解释变量Xj在回归模型Mk之外;πj表示解释变量Xj进入回归模型的先验概率,一般假设π1=π2=…=πp=π。若π=0.5,式(14)就等同于均匀先验式(12);若π>0.5,表示解释变量进入回归模型的可能性大,这种先验意味着对大模型的偏好;若π<0.5,表示解释变量进入回归模型的可能性小,这种先验则意味着对大模型的惩罚。
(四)求解边际似然
方便起见,将边际似然式(5)中关于模型的信息去掉,边际似然简化为:
p(D)=∫p(D|θ)p(θ)dθ
(15)
下面介绍在BMA应用中,两类常用的求解边际似然方法:近似算法和随机模拟算法。近似算法主要是拉普拉斯方法(Laplace’sMethod),而随机模拟算法则包括蒙特卡洛模拟(MonteCarlo,MC)和马尔科夫链蒙特卡洛模拟(MarkovChainMonteCarlo,MCMC)两种方法。
1.拉普拉斯方法。Tierney和Kadane提出了拉普拉斯方法[7]。该方法分两步进行:
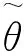
(16)

p(θ|D)=exp(l(θ))
(17)
其次,运用基本边际似然等式(Basicmarginallikelihoodidentity,BMI)求解边际似然:
(18)
(19)
以上是求解边际似然的拉普拉斯方法,p(D)1就是边际似然的拉普拉斯近似。

(20)
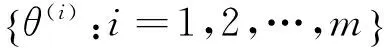
(21)
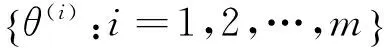
(22)
其中p(θ(i))/p*(θ(i))表示样本点θ(i)处的重要性权重,式(22)就是求解积分的重要性抽样方法(ImportanceSampling,IS)。利用重要性抽样求解积分具有悠久的历史,但其效率很大程度上依赖于选择合适的建议分布。在θ维度不高的情况下,建议分布选择T分布则可以取得较好的估计效果。θ维度较高时,有包括Meng和Wong的桥抽样(Bridgesampling)、Gelman和Meng的路径抽样(Pathsampling)、Chen和Shao的比率重要性抽样(Ratioimportantsampling)等方法可供选择。
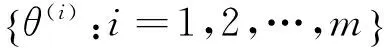
(23)
由此可见,边际似然是一种调和均值估计,属于一致估计,但由于似然函数倒数的方差并不总是有界的,所以该估计的有效性较差。
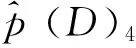
(24)
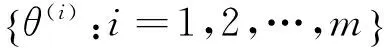

(25)
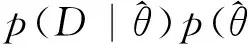
(五)模型搜索策略
利用近似或模拟等方法可以得到单个模型的边际似然,但当备选模型的数量巨大时,要求出所有模型的边际似然乃至后验概率,在计算上是不可能完成的。在这种情况下,可以采用模型搜索策略,搜索重要的模型构成模型空间的一个子集,然后在这个子集基础上进行贝叶斯模型平均。下面介绍三种模型搜索策略:Occam窗口方法、逆跳马尔可夫链蒙特卡罗方法(Reversible Jump Markov Chain Monte Carlo,RJMCMC)、马尔可夫链蒙特卡罗模型综合方法(Markov Chain Monte Carlo Model Composition,MC3)。
1.Occam窗口方法。Madigan和Raftery提出用Occam窗口方法选择一个模型子集[11]。令A表示模型空间{M1,M2,…,MK}。在筛选模型时,有以下两条准则:
第一,将后验概率非常低的模型删掉,模型后验概率的高低是相对的,如果具有最大后验概率的模型Mk*与模型Mk后验概率相比超过一个阈值,比如20倍,就认为Mk后验概率非常低,考虑将这个模型删掉。也就是说,如果模型Mk属于集合:
(26)
就将模型Mk从模型空间A中删掉,这里C是由研究者选择的一个阈值。
第二,将后验概率较低的复杂模型删掉。这与Occam剃刀原理相似,即“如无必要,勿增实体”。对于一个复杂模型,如果其子模型具有更高的后验概率,就保留子模型而将原模型删掉。也就是说,如果模型Mk属于集合:
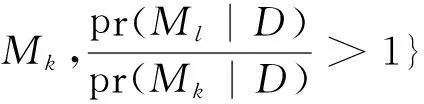
(27)
就将模型Mk从模型空间A中删掉。经过处理,模型空间中备选模型的数量大大减少,式(1)简化为:
(28)
这里 A3=A/(A1∪A2)。
2.逆跳MCMC方法。如果说MCMC方法促进了现代贝叶斯统计学的复兴,那么Green提出的逆跳MCMC方法则被视为贝叶斯分析的革命。由逆跳MCMC方法构建的马氏链不仅可以在单个模型的参数空间内进行转移,还可以在不同模型、不同维度参数空间之间实现跳跃,从而为BMA模型搜索提供强大工具。设逆跳MCMC当前模型状态为k,参数状态为θk, θk的维度为dk,那么从当前状态(k,θk)向下一状态转移的步骤如下:
步骤1从模型建议分布w(k,k*)中,生成一个建议模型k*。
步骤2从建议分布q(μ|θk,k,k*)中,生成随机向量μ。


α=
(29)
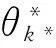
α=
(30)
3.MC3方法。Madigan和York提出马尔可夫链蒙特卡罗模型综合算法对模型进行抽签[12]。MC3方法倾向于抽取后验概率较高的模型,在一定数量的抽签后,能保证抽签结果收敛于基于所有模型的结果。与逆跳MCMC算法相似,MC3方法也是构造一条关于模型的马式链:M(1),M(2),…,M(N),并且这条马氏链的平稳分布就是模型的后验概率分布。为了构造这样的马氏链,要为任意一个模型定义相邻的模型空间,用以从中抽取备选模型。以线性模型为例,第s+1次从如下模型空间中等概率地抽取备选模型:当前模型M(s)、当前模型M(s)删减一个解释变量的模型、当前模型M(s)增加一个解释变量的模型。备选模型生成后,以如下接受概率判断是否接受备选模型M*:
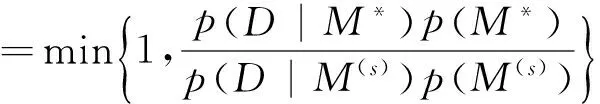
(31)
其中p(D|M*)和p(D|M(s))是边际似然,可以用Laplace、MC或MCMC等方法计算得到。如果假设所有模型先验概率相等,那么式(31)就简化为计算两个模型的贝叶斯因子:p(D|M*)/p(D|M(s))。George和McCulloch提出了与MC3相似的模型搜索策略,即随机搜索变量选择(Stochasticsearchvariableselection,SSVS)。在对模型抽签时,MC3会移除一个解释变量,但在SSVS中,所有解释变量被赋予一个概率,一个解释变量不会真正移除,而是以很大的概率趋于零。
四、大数据背景下贝叶斯模型平均的应用前景
在大数据背景下,借助于便捷的统计软件工具,BMA在国内外得到了广泛应用,特别是考虑到大数据价值的稀疏性,范剑青提出利用多个模型拟合数据,然后按照系统的观点利用模型平均方法将各模型结果综合起来,提取大数据的内在价值*2015年12月20日,范剑青在中国人民大学统计与大数据研究院暨大数据论坛做了题为“大数据人才培养:复旦方案”的报告。这里的观点是笔者根据报告的部分内容整理得到的。。目前,BMA的应用领域包括医学健康、计量经济学、工程技术、气象预报、水文地理等。
在医学健康方面:Volinsky等人研究了美国成年人的中风死亡因素,发现应用BMA于Cox比例风险模型(Proportional hazard model),可以避免逐步回归方法忽视的模型不确定性,改善对中风的预测,同时改进潜在中风患者的风险评价;Annest等在癌症与基因相关性的研究中,发现通过BMA可以选择数量较少的预测基因,但仍能对癌症的复发和转移进行有效预测;Bobb等人采用1987年至2005年美国105个城市的相关数据,构建了一组时间序列模型,估计高温天气对人类死亡率的影响,然后利用BMA将这些模型的结果进行综合,从而系统地解决了模型选择的不确定性问题;Carroll等人利用BMA方法研究了美国乔治亚州不同区域肠癌的影响因素,发现在乔治亚州的北部郡县,中产阶级的收入和非裔人群比例是肠癌的重要预测变量;在乔治亚州的南部,贫困线下人口比例和非裔人群比例是肠癌的重要影响因素[13]。
在计量经济学方面:BMA应用成果丰硕,Fernández等人利用BMA研究了跨国经济增长回归模型,发现拥有不同协变量的回归模型后验概率相差不大,证明模型不确定性的确存在,其实证结果支持萨拉伊马丁 的“乐观”结论,即多组协变量在解释跨国经济增长中具有重要作用;2008年,Wright在《计量经济学》发表文章,提出了对汇率预测的随机游走模型进行贝叶斯模型平均,研究发现模型平均的预测效果比单一模型要好;Wright又使用BMA对单一时间序列预测模型进行了综合, 发现这种方法对美国通胀率的预测优于简单平均的方法, 也优于单一时间序列预测模型;Jacobson和Karlsson使用类似的方法预测了瑞典的通胀;Eicher等利用BMA方法,综合考虑几种关于外商直接投资(Foreign Direct Investment,FDI)的模型,并且进一步将BMA扩展为HeckitBMA,解决了模型选择偏倚问题。
中国学者陈伟和牛霖琳运用BMA对中国通货膨胀率进行建模,并对样本外通胀进行预测,发现在均方根误差标准下,BMA方法的预测优于AR模型、主成分分析模型、菲利普斯曲线模型、利率期限结构模型等单一模型[6];王亮和刘金金采用BMA方法,使用1970—2007年的省际数据,对影响中国经济增长的因素进行了分析,发现高等教育发展阶段、工业化推进速度、对外开放程度、东部区位优势、消费能力和对内开放水平等 6 个解释变量对中国经济增长具有长期、持续和稳健的影响[14];朱慧明等人采用逆跳MCMC方法选择分位数自回归模型的阶次,沪深300指数的实证研究显示,贝叶斯方法可以有效地识别分位数回归的阶次并进行参数估计;司明和孙大超采用BMA方法分析发达国家主权债务危机成因,发现金融危机冲击、经济增长率下降、失业率升高、人口老龄化和政府预算收入降低是债务危机爆发的主要原因;高丽君采用中小企业信用数据,利用传统生存模型、Bootstrap生存模型和BMA生存模型估计中小企业信用违约情况,研究发现BMA生存模型结果准确率较高,Bootstrap生存模型次之,传统生存模型准确率最低;李佳蓓等人对多元线性回归问题中的变量选择方法进行了研究,改进了现有的贝叶斯自适应抽样方法,数据仿真发现改进后的方法预测效果比改进前更好[15]。
此外,在工程技术领域,Raftery和Kárny在传统BMA方法基础上,提出了动态模型平均技术(Dynamic Model Averaging,DMA),并将其运用到冷轧机输出的在线预测中;王华伟等人采用BMA方法,研究了不同失效模式对航空发动机可靠性的影响;在气象预测领域,Raftery等将BMA引入到对各种气象参数的预测中,目前BMA已经在气温、气压、风速、能见度等预测中得到广泛应用。Fang和Li在运用气候大数据对过去1 000年气候变化模拟时,利用BMA方法综合考虑了不同气候模型的模拟结果,发现BMA方法能够发挥各模型的优势,得到更可靠的气候变化模拟结果;在水文地理方面,梁忠民等人发现基于BMA的水文模型合成预报,不仅可以提供精度较高的均值预测,而且可以通过预测分布评价预测的不确定性。
五、结束语
从1978年Leamer提出贝叶斯模型平均方法至今,已有逾30年的历史,在这30多年里,贝叶斯模型平均方法渐趋成熟,其应用也愈加广泛。笔者回顾了贝叶斯模型平均的发展历程,介绍了贝叶斯模型平均的基本原理,综述了大数据背景下贝叶斯模型平均的理论突破,并介绍了大数据背景下贝叶斯模型平均在各领域中的应用。
贝叶斯模型平均方法不偏好也不摒弃各个模型,而是对各模型结果进行综合,以期发挥各模型优势,融合更多信息。贝叶斯模型平均的魅力不仅在其对模型结果的综合,还在于这种方法本身所蕴藏的贝叶斯智慧。贝叶斯模型平均改变了人们对模型比较和模型选择的传统认识,是对经典建模理论的有益补充。本文的目的是系统地介绍贝叶斯模型平均方法的理论进展,为国内学者应用贝叶斯模型平均方法提供参考。笔者相信在大数据背景下,将贝叶斯模型平均方法应用到中国社会、经济各领域的数据分析中,将会得到更多有用的信息和有价值的结论。
参考文献:
[1]Breiman L. Statistical Modeling: The Two Cultures (with Comments and a Rejoinder by the Author)[J]. Statistical Science, 2001 (3).
[2]Clyde M, George E I. Model Uncertainty[J]. Statistical Science, 2004(1).
[3]刘乐平, 高磊, 杨娜. MCMC 方法的发展与现代贝叶斯的复兴[J]. 统计与信息论坛, 2014 (2).
[4]Hoeting J A, Madigan D, Raftery A E, et al. Bayesian Model Averaging: A Tutorial[J]. Statistical Science, 1999(4).
[5]Gneiting T, Raftery A E. Weather Forecasting with Ensemble Methods[J]. Science, 2005(10).
[6]陈伟,牛霖琳. 基于贝叶斯模型平均方法的中国通货膨胀的建模及预测[J]. 金融研究,2013(11).
[7]Tierney L, Kadane J B. Accurate Approximations for Posterior Moments and Marginal Densities[J]. Journal of the American Statistical Association, 1986(3).
[8]Newton M A, Raftery A E. Approximate Bayesian Inference with the Weighted Likelihood Bootstrap[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1994(1).
[9]Chib S. Marginal Likelihood from the Gibbs Output[J]. Journal of the American Statistical Association, 1995(12).
[10]Chib S, Jeliazkov I. Marginal Likelihood From the Metropolis-Hastings Output[J]. Journal of the American Statistical Association, 2001(3).
[11]Madigan D, Raftery A E. Model Selection and Accounting for Model Uncertainty in Graphical Models Using Occam's Window[J]. Journal of the American Statistical Association, 1994(12).
[12]Madigan D, York J, Allard D. Bayesian Graphical Models for Discrete Data[J]. International Statistical Review/Revue Internationale de Statistique, 1995(8).
[13]Carroll R, Lawson A B, Faes C, et al. Bayesian Model Selection Methods in Modeling Small Area Colon Cancer Incidence[J]. Annals of Epidemiology, 2016(1).
[14]王亮, 刘金全. 中国经济增长的决定因素分析——基于贝叶斯模型平均 (BMA) 方法的实证研究[J]. 统计与信息论坛, 2010(9).
[15]李佳蓓,朱永忠,王明刚. 贝叶斯变量选择及模型平均的研究[J]. 统计与信息论坛,2015(8).
(责任编辑:郭诗梦)
On Theoretical Breakthrough and Application Prospect of BMA in Context of Big Data
GAO Lei1,LIU Le-ping1,LU Zhi-yi2
(1.Center for Big Data Analysis, Tianjin University of Finance and Economics, Tianjin 300222, China;2.School of Science, Tianjin University of Commerce, Tianjin 300134, China)
Abstract:Model comparison and selection uncertainty issue is very common in the big data analysis. The Bayesian model averaging (BMA) treats model as stochastic variable and assigns prior and posterior probability for it in order to account for model uncertainty. BMA weights the results of each model by their posterior model probability,and in the end obtatin more robust results. In this paper, we briefly describe the origins and developments of BMA, introduce the paradigm of BMA, and then discuss new progresses of BMA. Some important aspects of application are given in the context of big data.BMA combined with complex data analysis methods will provide new insights in our big data research methods.
Key words:big data; model uncertainty; Bayesian model averaging; MCMC
收稿日期:2016-01-18;修复日期:2016-04-20
基金项目:国家自然科学基金项目《Solvency II 框架下非寿险准备金风险度量与控制研究》(71171139);《多重风险相依情形下的最优保险问题研究》(71371138);《Basel III 框架下商业银行监管资本套利识别研究》(71303169);《逆周期资本监管框架下考虑跳跃行为的信用风险度量研究》(71401069);天津财经大学研究生科研资助计划(2014TCB03)
作者简介:高磊,男,山东德州人,博士生,研究方向:精算与风险管理;
中图分类号:C829.29∶O212.8
文献标志码:A
文章编号:1007-3116(2016)06-0014-09
刘乐平,男,江西萍乡人,经济学博士,教授,博士生导师,研究方向:贝叶斯数据分析,精算与风险管理;
卢志义,男,内蒙古包头人,经济学博士,副教授,硕士生导师,研究方向:精算与风险管理。
【统计理论与方法】
