确定双横臂悬架侧倾中心的方法及其差异分析

叶锦文，杨　蔓，杨建国

（广州汽车集团股份有限公司汽车工程研究院，广州　510640）



确定双横臂悬架侧倾中心的方法及其差异分析

叶锦文，杨蔓，杨建国

（广州汽车集团股份有限公司汽车工程研究院，广州510640）

摘要：介绍确定双横臂悬架侧倾中心的两种不同方法，并进行对比分析。用CATIA建立双横臂悬架刚体运动学模型，用两种方法分别求出不同轮心位置对应的侧倾中心高度，对比其差异程度。最后基于ADAMS的计算结果对比两种方法的准确度并进行理论分析，指出产生差异的根本原因和各方法的适用条件。

关键词：双横臂悬架；侧倾中心；方法；CATIA；ADAMS

悬架侧倾中心是分析车辆运动学的一项重要指标，对悬架的性能，整车的侧倾程度有明显的影响。悬架侧倾中心越高，质心到车身侧倾轴线的距离越小，车辆弯道行驶的侧倾角越小，乘员的主观感觉越安全。仿真分析表明，车辆质心高度对稳态回转的车身侧倾梯度有显著的影响，其灵敏度为每毫米0.21°/（m·s-2）[1]。因此，侧倾中心高度对车身侧倾梯度有明显的影响。当然侧倾中心过高也会产生不利影响：容易导致轮胎偏磨，同时悬架对路面的粗糙程度更加敏感。因而合适的侧倾中心位置是保证悬架性能的基本条件。正确确定悬架侧倾中心，可以直观分析悬架导向机构对侧倾中心的影响，进而分析对悬架性能的影响，为悬架结构设计提供指导。根据德国法规标准DIN 70000规定：侧倾中心位于经过轮心的垂直平面内，在该点施加作用于簧上质量的侧向力不会引起车身侧倾[2]。

1　确定侧倾中心的方法及特点

《汽车理论》介绍了用“三心定理”确定双横臂独立悬架侧倾中心的方法[3]。但是适用该方法的双横臂悬架具有特殊性，即上摆臂、下摆臂的旋转轴线在后视图的投影均为一个点，如图1所示。这种特殊结构的双横臂悬架在车上几乎没有应用。因此，该方法具有局限性。目前车上应用的双横臂悬架为了提高车辆性能，设计的上摆臂和下摆臂的在侧视图中有一个角度。《The Automotive Chassis》介绍了确定这种布置形式的双横臂悬架的侧倾中心的方法（下文称作方法二）：在侧视图中，经上摆臂外球铰点E1，下摆臂的外球铰点G1，分别作地面的垂线，与上摆臂旋转轴线C1G2交于E2，与下摆臂的旋转轴线交于G2。在后视图中，直线E1E2与直线G1G2交于P点，P点与轮胎接地中心的连线与悬架纵向对称面交于RO，RO即为侧倾中心[4]。如图2所示。

行业常用的方法（下文称作方法一）是：作直线E1E2、G1G2分别垂直于C1C2和D1D2，直线E1E2、G1G2交于P点，连接P点和轮胎接地点的直线与车辆纵向对称面的交点RO为侧倾中心，如图3所示。该方法可认为是由“三心定理”扩展得到。该方法与方法二的区别在于E2、G2点确定方法不一样。

上述两种方法得到的E2、G2点必然不一样，交点P因此不同，侧倾中心RO也不一样。

2　侧倾中心差异对比

用CATIA建立双横臂悬架刚体运动学模型，拓扑关系如下[5]：上摆臂与副车架用旋转副，上摆臂与转向节用球副，下摆臂与副车架用旋转副，下摆臂与转向节用球副，转向节与转向横拉杆用球副，因不需要转向功能，转向横拉杆用万象副与副车架连接，减振器活塞杆与副车架用万象副，活塞该与减振器套筒用圆柱副，减振器套筒与下摆臂用万象副，车轮与转向节固定连接[6]。双叉臂悬架部分硬点如表1所示。

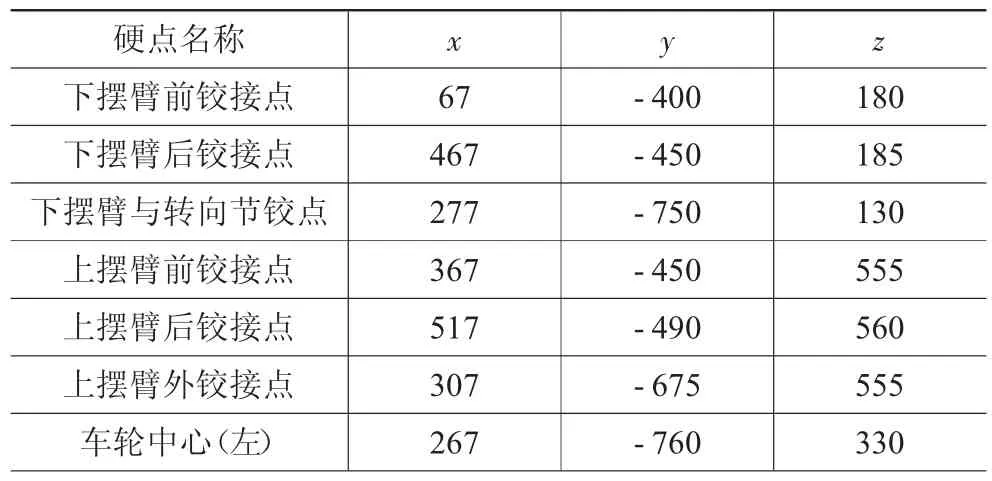
表1　双叉臂悬架部分硬点坐标　mm

分别用上述两种方法求出的不同轮心位置时的侧倾中心，然后测得侧倾中心高。轮胎运动过程中，两种方法侧倾中心高的变化趋势是一致的，但是数值存在差异，如表2所示。

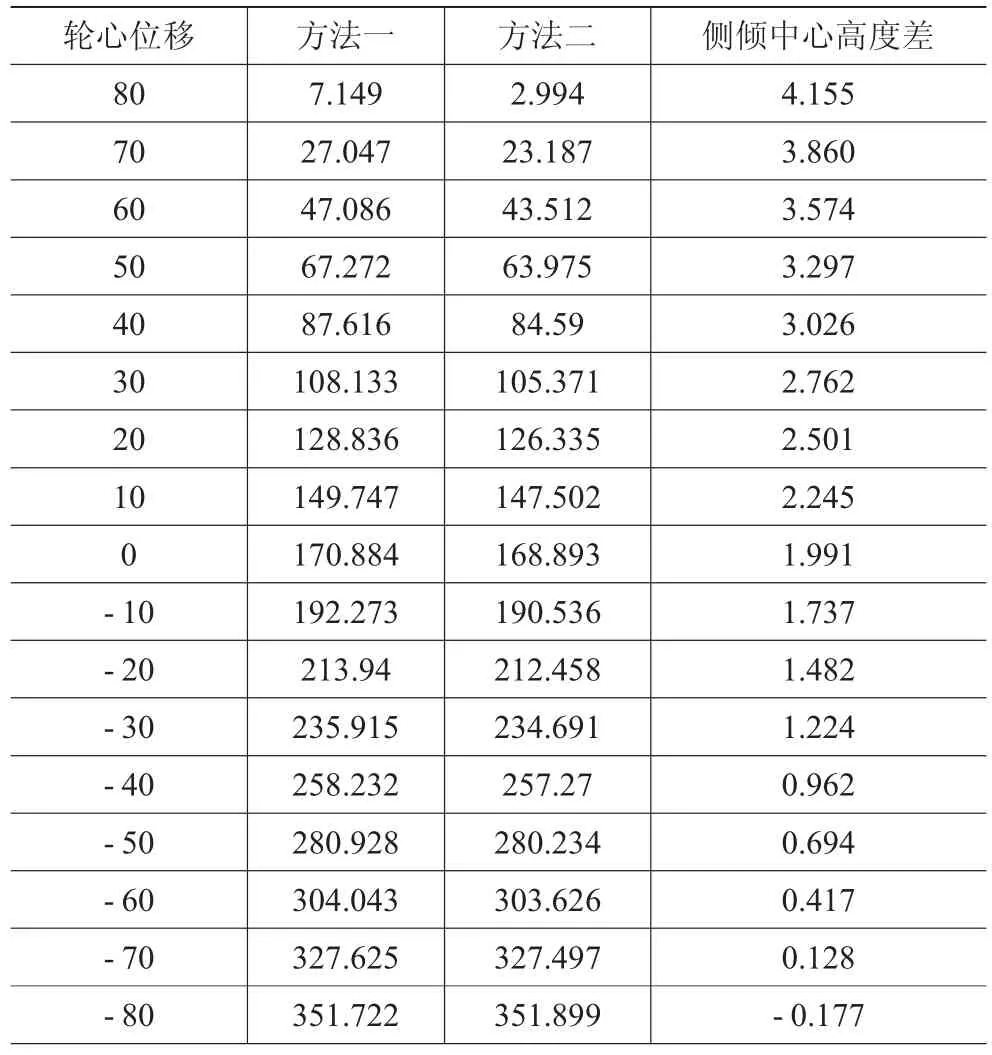
表2　侧倾中心高及其差值　mm

侧倾中心高的差异是因两种方法所得的E2、G2点位置不同引起的。因此，上摆臂及下摆臂的空间布置位置决定侧倾中心高的差异。某些布置条件下，上述两种方法得到的E2点和G2点在后视图上有显著差别，因而得到的侧倾中心位置有很大差异[7-8]。更改上摆臂的硬点坐标（如表3所示），其余硬点不变。上述两种方法得到的侧倾中心高及其差值如表4所示。

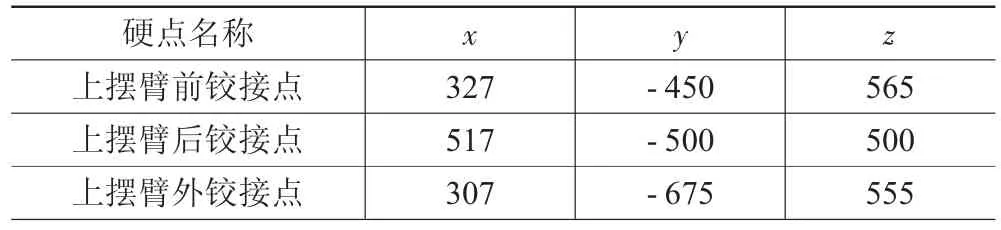
表3　变更后的上摆臂硬点坐标　mm

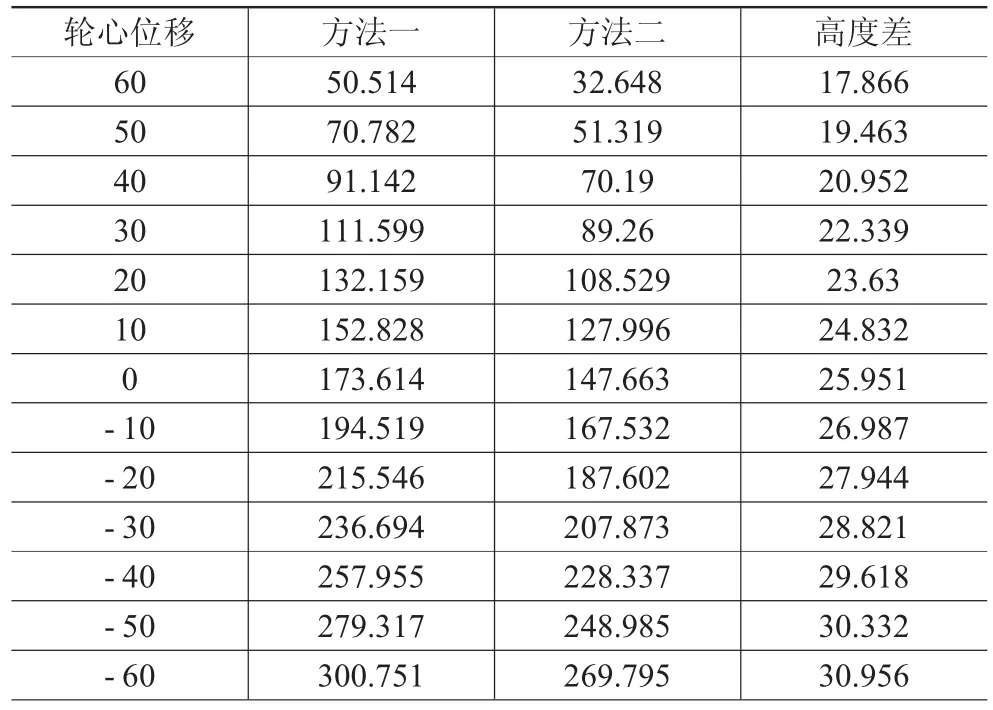
表4　变更上摆臂硬点坐标后的侧倾中心高及差值　mm

由表4可知，侧倾中心高度差在轮跳为0时（设计状态）达到26 mm；在-60～60 mm的轮跳范围内，最大值约31 mm，最小值约17.9 mm。这种差异对侧倾中心来说是巨大的。显然，其中一种方法不适合用于研究悬架侧倾中心。

3　双横臂悬架模型侧倾中心的比较分析

3.1基于ADAMS仿真的结果比较

用ADAMS建立双横臂悬架的运动学模型[9]，模型的硬点坐标及拓扑结构与CATIA模型一致，模型的轮胎刚度为108N/mm，即认为轮胎是刚性的，避免轮胎变形对侧倾中心产生影响。仿真所得侧倾中心高及与上述两种方法的对比结果如表5所示，其中△1为ADAMS仿真结果与方法一之差；△2为ADAMS仿真结果与方法二之差。

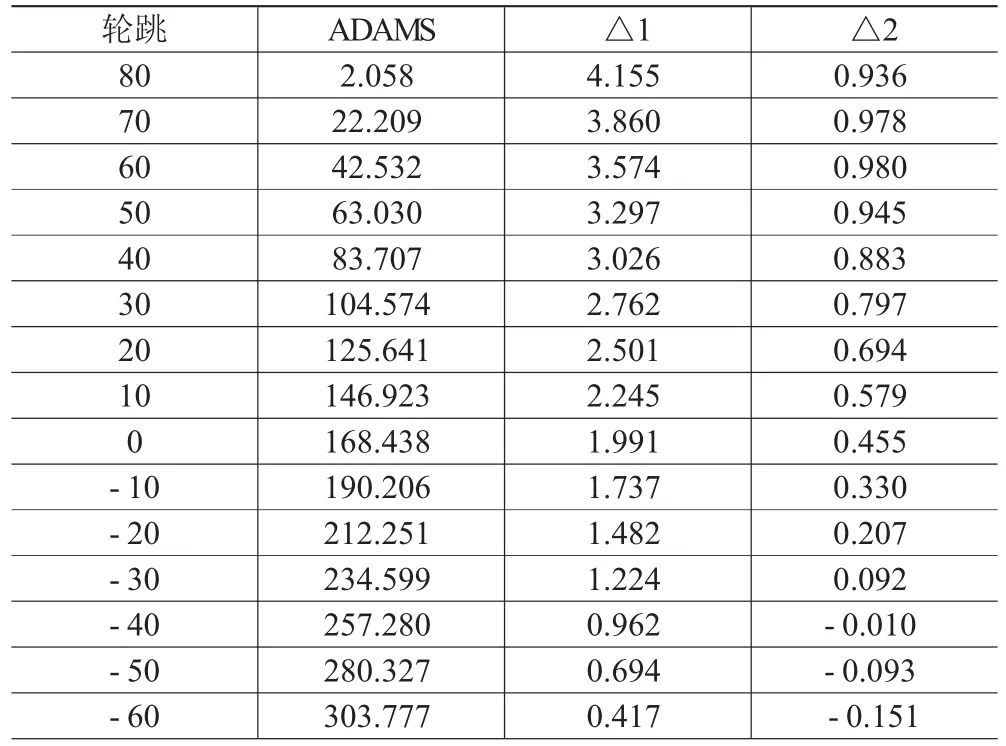
表5　ADAMS侧倾中心高仿真结果及比较　mm

根据表3更改上摆臂的硬点坐标，侧倾中心高与ADAMS仿真结果对比如表6所示。

表6　ADAMS侧倾中心高仿真结果　mm

由表5可知，以ADAMS仿真结果为基准，方法二设计位置（轮跳为0）的误差为0.46 mm，最大误差0.98 mm，误差均在1 mm之内；方法一设计位置误差1.99 mm，最大误差为4.16 mm。方法二与ADAMS的仿真结果十分接近。

由表6可知，以ADAMS仿真结果为基准，方法二的误差明显小于方法一的误差；与ADAMS的仿真结果比较，轮心在-30～30mm之间时，差别较小。悬架设计关注的是设计状态及其附近位置的侧倾中心，一般正负20mm即可，超出此范围的车身侧倾主要依靠稳定杆控制。

3.2方法一与方法二差异的理论分析

根据双横臂悬架的运动学特性（如图3所示），点E1、G1分别绕轴线C1C2、D1D2旋转，其速度方向分别垂直于平面E1G1G2、平面G1D1D2，速度大小等于各自旋转轴线的角速度分别与E1E2、G1G2的乘积。因此，点E1、G1的速度矢量不共面，点E1、G1的速度矢量之间不存在瞬心[10]。对于方法一，直线E1E2、G1G2是异面直线，没有交点。因此，用一假定的角速度矢量ω与E1P、G1P乘积得到的速度矢量与点E1、G1速度矢量在经过轮心的横向平面上投影得到的速度分量的方向不一定一样（如图4所示），即P点不是E1、G1在经过轮心的横向平面上的瞬心。所以，RO点不是侧倾中心。由此可知，该方法在理论上是错误的。

车轮组件在经过轮心的横向平面的瞬心就是点E1、G1的速度矢量在该平面的投影得到的速度分量的瞬心，即把E1、G1的速度矢量先投影到经过轮心的平面上，再求解两个分量的瞬心。E1的速度矢量V投影到经过E1的横向平面E1E2E3E4内，即V1（如图5所示），平面与直线C1C2的交点为E2。因为上摆臂E1绕轴线C1C2转动，所以速度矢量V垂直平面E1C1C2，所以VE1垂直E1E2，因为V1是速度矢量在平面E1E2E3E4的投影，所以VV1垂直平面E1E2E3E4，所以VV1垂直E1E2。因为E1E2垂直VE1，E1E2垂直E1V1，所以E1E2垂直平面VV1E1，所以E1E2垂直V1E1。E1点的速度分量与E1E2垂直，因此点E1在该平面的瞬心一定在直线E1E2上，同理，G1速度分量的瞬心在直线G1G2上。所以要同时满足点E1、G1速度分量方向的条件，点P要同时在直线E1E2和直线G1G2上，即直线E1E2和直线G1G2交点。此方法即方法二。

经分析可知，方法一理论上是不正确的。但是，如果x、y、z上摆臂的前点和后点以及下摆臂的前点和后点的z坐标差别均较小，那么方法一和方法二得到的E2、G2点在横向平面的投影差别也较小，得到的侧倾中心差异较小。如果上摆臂或者下摆臂前后点的z坐标差别较大，那么上述两种方法的侧倾中心差异将很明显。同理，y坐标也是如此。如果前点和后点的y坐标、z坐标均一样，这种悬架就是《汽车理论》介绍双横臂悬架侧倾中心所用的特殊结构的悬架。此时，方法一、方法二、《汽车理论》介绍的方法，三者是一样的，P点因此也一样。

综上所述，虽然行业经常用方法一分析双横臂悬架的侧倾中心，但是该方法在理论上是错误的。另外，由于摆臂实际的前后点y、z坐标差别不会很大，方法一和方法二的差别因此不会很大，并且随轮跳变化的趋势也一样，即方法一的错误不明显。

3.3方法二与ADAMS差异的理论分析

ADAMS计算侧倾中心的方法如图6所示。在轮胎接地点施加单位的垂向力（垂直于路面），测量接地点在横向平面内产生的侧向位移和垂向位移，经过轮胎接地点且垂直于及地点位移方向的两条直线（左右轮各一条）的交点即侧倾中心。

方法二是依据瞬心的理论求得侧倾中心。根据瞬心的定义，车轮组件（车轮及转向节）认为是一个刚体，那么点E1、G1及车轮接地点之间没有相对运动。但是，实际上由于上下摆臂是空间布置的，在轮胎向上或者向下运动时，轮胎接地点并非轮胎上固定的点。该点会有变化，也就是轮胎接地点相对于E1、G1点是运动的，E1、G1及车轮接地点代表的车轮组件不是一个刚体。因此，根据E1、G1的瞬心P点计算的轮心接地点的速度，其方向与轮心接地点的真实运动速度矢量在横向平面投影（即图7中的ADAMS计算的位移矢量）的速度方向不一定一致。

方法二与ADAMS计算结果的差异由轮胎接地点的变化程度决定。根据经验，目前双横臂的布置形式在较大的轮跳范围内（可达±30 mm），轮胎接地点的变化均较小。因此，方法二适用于指导双横臂悬架设计。

3.4关于ADAMS计算侧倾中心方法的见解

依据侧倾中心的定义可知，侧倾中心是经过轮心的垂直平面内，车厢相对于地面的瞬时旋转中心。根据相对运动，该点也是地面相对于车身的瞬时旋转中心。如果该点也是左右车轮接地点的瞬心，那么左右车轮接地点在车身侧倾过程中，相对地面应该不动，即接地点应该是地面这一刚体上不动的两个点。事实上，车身侧倾时，轮距会有很小的变化，也就是左右车轮的接地点是有相对运动的。因此，ADAMS计算的侧倾中心并不是DIN7000所定义的侧倾中心，而是车身相对于车轮组件的侧倾中心。由于轮距的变化量相对轮距来说是很小的（通常在1%左右），因此可认为车身相对于车轮组件的侧倾中心近似等于车身相对于地面的侧倾中心。设计悬架时，通常更关注设计状态的侧倾中心位置。在车辆设计状态附近，轮跳产生的轮距变化通常更小。因此，ADAMS的结果更加准确。对于分析车辆性能，指导悬架设计，这一方法已经足够准确。

4　结论

根据上述分析结果，对于双横臂悬架有如下结论：

1）汽车行业定义的侧倾中心，其位置取决于悬架的导向结构，但是几乎没法通过悬架导向结构精确求解其位置，这一点对其它悬架也是适用的。

2）ADAMS计算的侧倾中心实际上是车身相对于车轮组件的侧倾中心，与行业定义的侧倾中心有区别，但两者的位置相差很小。因此，用车身相对于车轮组件的侧倾中心分析双横臂悬架的几何学或进行侧倾中心的定量分析是可行的，即ADAMS的计算结果足够准确。

3）方法二存在与ADAMS一样的误差，同时把接地点认为是刚性轮胎组件上点也产生一定的误差，但是这不影响它用于分析双横臂悬架的几何学，但是对悬架性能量化分析时须慎用。在某些特殊的情况下，方法二会产生比较明显的误差。

4）汽车行业广泛采用的分析双横臂侧倾中心的方法（即方法一），在理论上是错误的。只有在上下摆臂布置均比较特殊的情况，其结果才与真实值比较接近。一般情况下误差较大，最好不要使用该方法。

参考文献：

[1]于国飞，艾维全，王承，等.车辆稳态转向特性中车身侧倾角的影响因素[J].同济大学学报：自然科学版，2006，34（9）：1237-1241.

[2]耶尔森.赖姆帕尔.汽车底盘基础[M].张洪欣，余卓平，译.北京：科学普及出版社，1992：136-147.

[3]余志生.汽车理论[M].5版.北京：机械工业出版社，2010.5.

[4] Prof.Dipl.-Ing.J?rnsenReimpell，Dipl.-Ing. Helmut Stoll．The Automotive Chassis [M].Wurzburg：Vogel-Buchverlag，1999：160-166．

[5]王淑芳.基于CATIA的汽车悬架动态仿真[D].重庆：重庆交通大学，2007．

[6]李臣，司景萍.基于ADAMS/CAR的麦弗逊悬架建模与仿真[J].公路与汽运，2007（3）：8-10.

[7]刘进伟，吴志新，徐达.基于ADAMS/CAR的某轿车悬架优化设计[J].轻型汽车技术，2006（8）：4-7.

[8]罗鑫源，杨世文，杨军，等.基于ADAMS的双横臂悬架的仿真及优化[J].公路与汽运，2011（5）：9-11.

[9]汪随风，刘竞一.基于ADAMS的汽车前悬架仿真研究[J].上海汽车，2007（5）：29-32.

[10]郝桐生.理论力学[M].3版.北京：高等教育出版社，2003：194-198.

修改稿日期：2015-10-04

Methods and Their Differences Analysis on Determining Roll Center of Double Wishbone Suspension

Ye Jinwen, Yang Man, Yang Jianguo
（Automobile Engineering Institute，Guangzhou Automobile Group Co., Ltd, Guangzhou 510640, China）

Abstract：The authors introduce twodifferent methods ofdeterminingthe roll center ofdouble wishbone suspension and carry out the comparative analysis. They use CATIA to build the kinematic models of double wishbone suspension, find out the roll center height corresponding to different wheel center position by using the above two methods and compare their different extend. Finally, based on the computing results using ADMAS, they comparatively analyze the accuracy of the two methods and carry out the theoretical analysis, as well as point out the basic reasons of comingintodifferences and the applicable conditions ofeach method.

Key words:double wishbone suspension; roll center; method; CATIA; ADAMS

中图分类号：U463.33

文献标志码：A

文章编号：1006-3331（2016）02-0010-05

作者简介：叶锦文（1987-），男，车辆动力学工程师；主要从事车辆动力学相关分析工作。