Lebesgue控制收敛定理的证明及应用

张孟娟,金瑾

（1.贵州工程应用技术学院，a.理学院，b.毕节循环经济研究院，贵州 毕节 551700)

Lebesgue控制收敛定理的证明及应用

张孟娟1a,金瑾1b

（1.贵州工程应用技术学院，a.理学院，b.毕节循环经济研究院，贵州 毕节 551700)

通过引入Lebesgue积分与R iemann积分的关系，仔细比较两个积分的优越性，进而详细地阐述了Lebesgue控制收敛定理的证明及其应用。首先给出了Lebesgue控制收敛定理并对其进行证明，其次再举例说明其基本的应用，最后，指出该定理的不足之处并给出条件稍宽松的定理，从而可为解题带来便利，为理解并掌握Lebesgue控制收敛定理及应用提供指导。

Lebesgue积分；Riemann积分；极限

1 引言

Lebesgue控制收敛定理是在解决积分号与极限号的交换次序中常用到的工具之一，是在求函数列积分的极限时常用的基本手段之一，也是比Riemann积分更广泛的定理。在谈到极限号与积分号的交换时，基本上都是以此定理作为研究手段，并且在证明不等式、函数相等、数列收敛及积分的极限等方面起着举足轻重的作用。并且作为实变函数的核心内容，也在实际生活中有着广泛应用。

2 Lebesgue积分与Riemann积分的关系

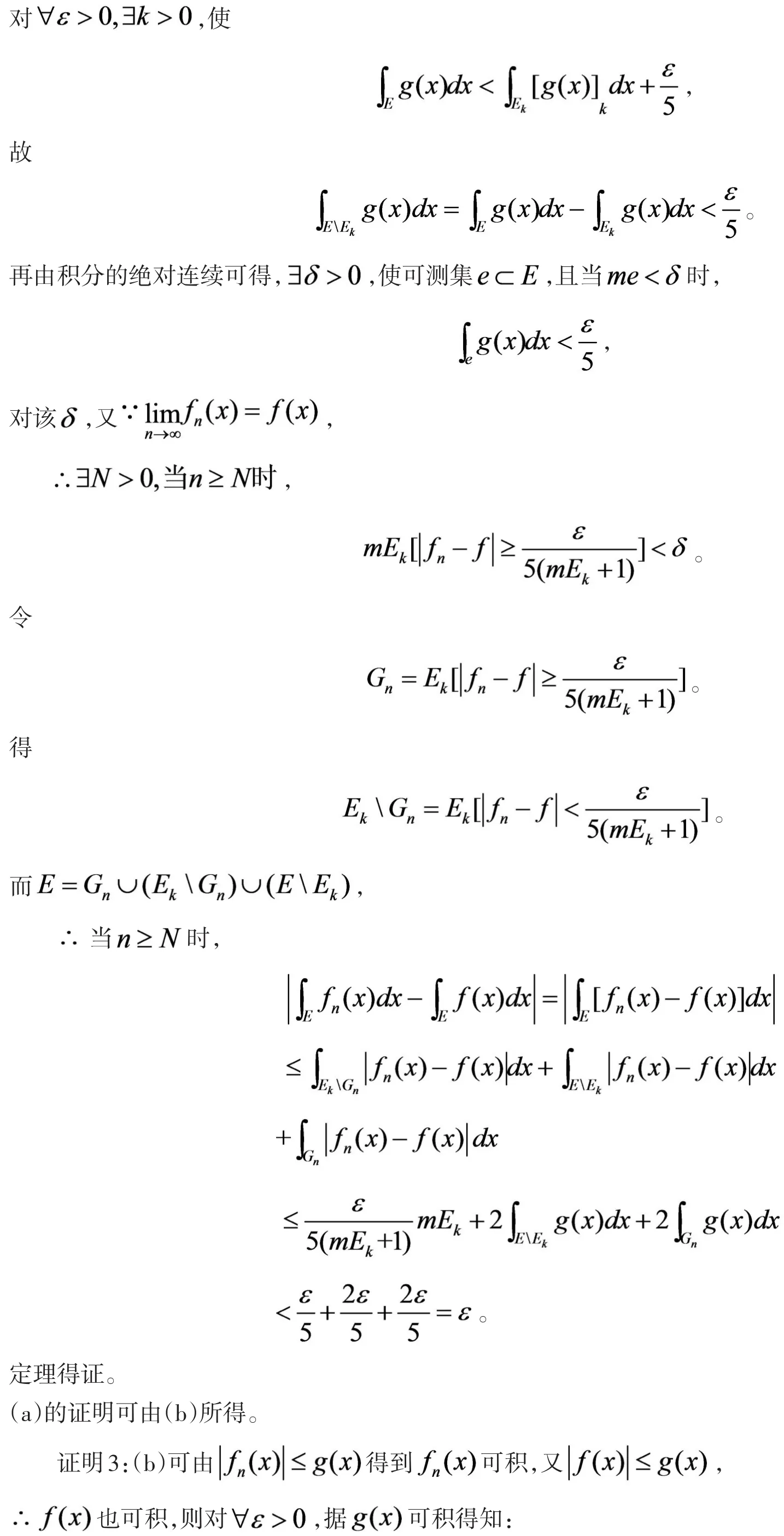
5 结论

参考文献：

[1]金瑾．测度与积分理论及其新研究[M]．贵阳：贵州民族出版社，2004:97-123．

[2]程其襄，张奠宙，魏国强，胡善文，王漱石．实变函数与泛函分析基础(第三版)[M]．北京：高等教育出版社，2010:53-119．

[3]黄祖达，李应求，肖宏芳，张敏．控制收敛定理的推广及其应用[J]．湖南文理学院学报(自然科学版)，2013（2）：14-15．

[4]周相泉，董桂真，张兴田．积分连续性定理和Lebesgue控制收敛定理的新证明[J]．聊城师院学报(自然科学版),1995（2）:09-10．

[5]郑维行，王声望．实变函数与泛函分析概要[M]．北京：高等教育出版社，1989:136-144．

[6]刘晓辉，康叔卫．Lebesgue控制收敛定理及应用[J]．和田师范专科学校学报，2006（6）：231．

[7]周民强．实变函数解题指南[M]．北京：北京大学数学科学学院出版社，2007:218-248．

Proof and App licationsof Lebesgue ControlConvergence Theorem

ZHANGMeng-juan1a,JIN Jin1b
(1a.SchoolofScience,Guizhou University of Engineering Science,Bijie,Guizhou551700,China;2b.Bijie Recycling Economy Research Institute,Guizhou University of Engineering Science,Bijie, Guizhou551700,China)

By introducing the relationship between Lebesgue integraland Riemann integral.The superiority of carefully compare two points,and in detail elaborated the Lebesgue control convergence theorem is proved and its application.Firstly,giveing the Lebesgue dominated convergence theorem and its proof,then illustrate its basic application.Finally,it is pointed out that the theorem of the deficiencies and give conditions slightly looser theorem,which can bring convenience for us to solve problems.Through the browsing of thisarticle,the reader can understand and grasp the Lebesgue controlconvergence theorem and itsapplication.

Lebesgue Integral;Riemann Integral;Limit;Lebesgue Control Convergence TTheorem;Application

B84

A

2096-0239（2016）06-0125-09

（责编：任秀秀 责校：明茂修）

2016-08-11

贵州省教育厅重点项目“微分方程解的增长性理论及应用研究”，项目编号：（2015）392。

张孟娟（1992-），女，贵州毕节人，贵州工程应用技术学院理学院学生。研究方向：复分析。

金瑾（1962-），男（白族），贵州毕节人，贵州工程应用技术学院教授。研究方向：复分析。