空间曲线实例的解法剖析

刘涛

（贵州工程应用技术学院理学院，贵州 毕节 551700）

空间曲线实例的解法剖析

刘涛

（贵州工程应用技术学院理学院，贵州 毕节 551700）

空间曲线是微分几何的一个重要内容，因其抽象、知识点多，初学者往往感到难以掌握，不容易把各知识点融会贯通，对题目无处下手。根据不同的数学思想方法，从向量函数的性质、挠率公式、伏雷内公式、平面方程四种不同角度对微分几何的一个实例进行了剖析，较全面地介绍了空间曲线的相关知识点和相关思想方法的应用。

向量函数；伏雷内公式；曲率；挠率

微分几何是帮助学生由初等几何通向现代微分几何的桥梁，[1]在数学的专业学习中占有重要的地位。微分几何研究的主要内容是空间曲线和空间曲面，而空间曲线的学习又是理解空间曲面的基础。[2]在空间曲线学习过程中，同学们往往感觉难以灵活地运用相关知识来求解题目。在授课中我们可以选择一些经典实例，通过实例讲解来演示如何借助常用的数学思想方法，综合运用微分几何知识来求解相关题目。文章从不同的思想方法入手对一个空间曲线实例的解法进行了全面剖析。通过这个实例的讲解，可以巩固空间曲线的相关知识，提高综合运用数学知识的能力，增强对数学思想方法的认识和理解。

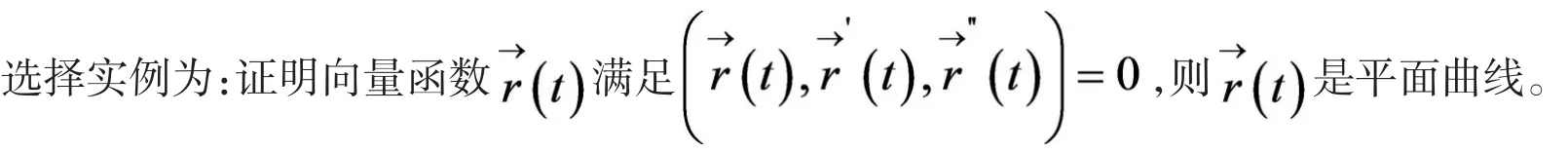
解析：对于这个实例，从相关的知识点来思考，即可以从向量函数的性质、挠率公式、伏雷内公式、[3]平面方程四个角度来考虑证明方法，然后再思考如何借助常用的数形结合、转化与化归、分类讨论、方程思想等数学思想方法组织证明步骤。

分析：此证明是根据向量函数的性质及几何意义进行的，在证明过程中需先构造一个曲线所在平面的法向量，用到了数学中有较高难度的构造方法，需要较强的分析能力和推理能力，对微分几何初学者来说是较难掌握的。

（2）根据转化与化归的数学思想证明：由空间曲线知识，可知一个空间曲线为平面曲线的充要条件

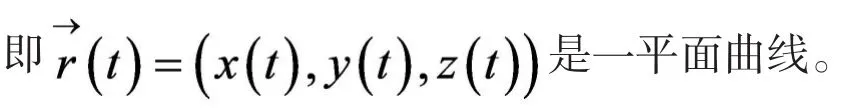
分析：证明过程中用到了向量函数的坐标表示，向量函数混合积的行列式表示，及高等代数中的矩阵、秩、线性相关的知识。借助平面曲线与平面的关系进行证明，证明过程涉及到多学科知识，这就要求具有综合运用多学科知识解决问题的能力。

小结

文章通过不同的数学思想方法对一空间曲线实例进行了详尽的剖析。在剖析过程中主要用到了一题多解的形式，但此处多解，不在于答案的多样性，而在于知识的融汇性，方法的灵活性，思维的层次性。通过这样的实例教学可以帮助同学们更好的理解和掌握空间曲线的相关知识及常用的数学思想方法。

[1]孙和军,赵培标,陈大广．微分几何的教学地位与方法[J]．高等数学研究,2011（1）:101-103．

[2]John Oprea．DifferentialGeometry and ItsApplications[M]．New Jersey:pearson education,Inc,2004：1-46．

[3]梅向明,黄敬之．微分几何[M]．北京:高等教育出版社,2008：29-52．

Abstuact:Curve in 3-space is an important content in differential geometry.It refersmany knowledges, so the studentswho justbegin study itusually feel hard to handle them.It is noteasy to solve questionswith the knowledges.A problem of curve in 3-space is solved in the articlewith vector function,tortsion formulas, Frenet Formulas and plane equation according to differentmathematical thoughts andmethods.Itusesmostof knowledgesof curve in 3-spaceandmeansofmathematics.

An Illustrative Exam p le of Curve in 3-Space

LIU Tao
(Schoolof Science,Guizhou University of Engineering Science,Bijie,Guizhou551700,China)

Vector Function;Frenet Formulas;Curvature;Torsion

B84

A

2096-0239（2016）06-0119-06

（责编：任秀秀 责校：明茂修）

2016-11-26

贵州省科学技术基金项目“基于格值逻辑的自动推理方法研究”，项目编号：黔科合J字LKB[2012]02号。

刘涛（1982-），男，山东青岛人，贵州工程应用技术学院理学院讲师。研究方向：微分几何、分形几何。