BDS/Galileo相位组合观测值优化选取

李克昭，赵磊杰，丁安民，李志伟，魏金本

(1.河南理工大学 测绘与国土信息工程学院，河南　焦作　454000；2.北斗导航应用技术协同创新中心，郑州　450052)

BDS/Galileo相位组合观测值优化选取

李克昭1，2，赵磊杰1，丁安民1，李志伟1，魏金本1

(1.河南理工大学 测绘与国土信息工程学院，河南焦作454000；2.北斗导航应用技术协同创新中心，郑州450052)

摘要：针对载波相位测量中，整周模糊度的快速正确求解受限于载波波长和测量噪声的问题，提出一种在保持模糊度为整数的前提下，利用BDS/Galileo载波相位虚拟组合观测值来增加波长并保持低测量噪声的方法，使之有利于模糊度的求解;根据组合观测值选取标准，对组合系数进行选取并获得几组有效观测值组合。结果表明，通过该方法能够获得满足特定性能的组合观测值。

关键词：BDS；Galileo；多频组合；整周模糊度

0引言

利用载波相位观测值实现高精度定位是全球导航卫星系统进行定位的主要方法和途径；而整周模糊度的确定是实现这一方法的关键技术之一。如何快速、准确地固定模糊度一直是这一领域的研究热点和难点。随着全球定位系统的快速组建，利用多频组合观测值实现模糊度快速固定的方法成为可能[1-2]。

当采用模糊度函数法解算基线向量时，极值点间距在相同几何卫星状态情况下与波长成正比；如果能获得波长较长的载波相位观测值，就可以降低先验初值精度的要求，增大搜索步长使计算时间明显缩短。

我国已成为伽利略卫星导航系统(Galileo navigation satellite system，Galileo)的股权友好国家[3]。北斗卫星导航系统(BeiDou navigation satellite system，BDS)是我国完全自主建设、运营的导航定位系统，将BDS和Galileo 2大系统相结合用于高精度的定位导航，具有重要的研究意义和实用价值。

Galileo和全球定位系统(global positioning system，GPS)类似，都采用被动式导航定位原理和扩频技术发送导航定位信号。Galileo提供4个载波频率：E2-L1-E1(即E1)频率为1 575.42 MHz，E6频率为1 278.75 MHz，E5a频率为1 176.45 MHz，E5b频率为1 207.14 MHz。BDS采用的载波频率分别为：B1频率为1 561.098 MHz，B2频率为1 207.14 MHz，B3频率为1 268.52 MHz[4-8]。考虑到Galileo各载波频率的服务对象以及观测噪声随组合频率数目的增加而增加，本文将Galileo系统的公共服务频率E1、E5a载波与BDS的B2、B3载波相位观测值进行组合，并构成新的组合观测值，而满足长波长、弱电离层和弱观测噪声的特性，使其有利于整周模糊度的确定。采用的载波频率的相关特性如表1所示；为了后文便于表示，对相应载波进行编号。

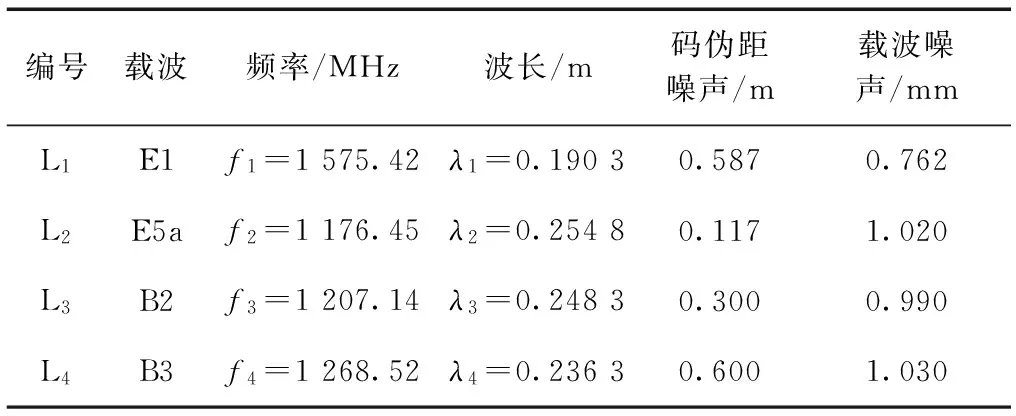
表1　采用的基本载波信号特征

1组合观测值的定义及误差分析

相位形式的载波相位观测方程可表示为

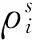
简化后的载波相位距离形式的观测方程(单位：m)为

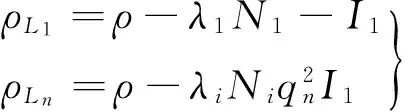
(2)

式中：ρ表示接收机天线相位中心至卫星的距离；I1为L1的电离层延迟；qn=f1/fn，n=2，3，4。

相应的组合观测值定义为

ρLc=αρL1+βρL2+γρL3+κρL4。

(3)

式中α、 β、 γ、 κ为相应的参数变量。

将式(2)带入式(3)可得

ρLc=ρ(α+β+γ+κ)-(αλ1N1+βλ2N2+

γλ3N3+κλ4N4)-I(α+βq2+γq2+κq2)。

(4)

为了保持几何距离不变和模糊度的整周特性，令：

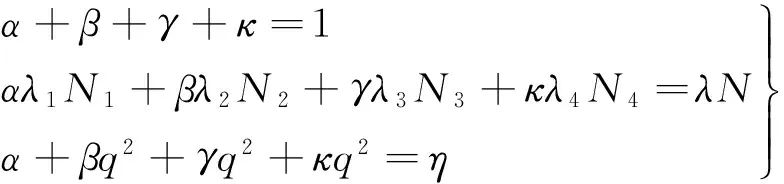
(5)

式中N为组合观测值的模糊度，则式(4)可表示为

ρLc=ρ-λN-Iη。

(6)

由式(5)可得

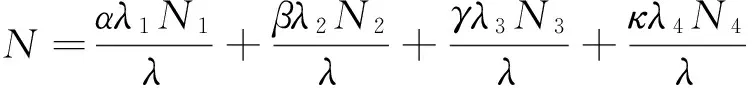
(7)

记

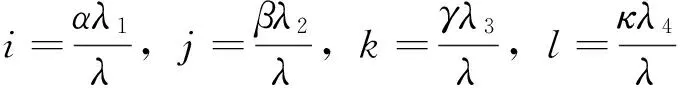
(8)

则组合观测值模糊度为

N=iN1+jN2+kN3+lN4。

(9)

为了保证N为整数，则i、j、k、l也应为整数，由式(8)变换后可得

(10)

将式(10)带入式(5)第1个式子可得组合观测值波长λ为

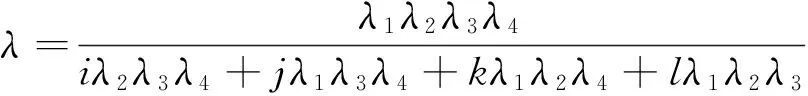
(11)

考虑到波长与频率之间的关系λ=c/f，c代表真空中的光速，结合式(11)可得组合观测值的频率f为

f=if1+jf2+kf3+lf4。

(12)

由式(1)、式(3)和式(8)可得载波相位值为

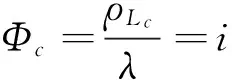
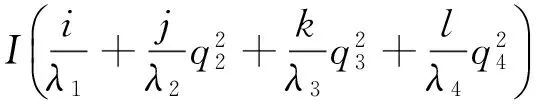
(13)

电离层延迟：由式(4)和式(10)以及频率和波长之间的关系可得组合观测值的电离层延迟为

Ic=I(α+βq2+γq2+κq2)=

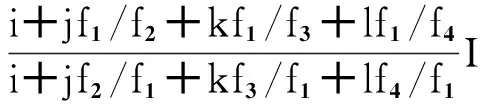
(14)

为了便于表示分析，记Ic=HI， 组合观测值电离层延迟系数为

(15)

设：载波相位测量噪声为σ；双差载波相位噪声为2σ；结合误差传播定律，组合观测值的噪声可表示为：

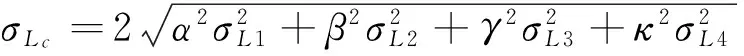
(16)

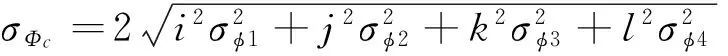
(17)

2组合观测值的选取

组合观测值的选取应考虑在保持一定的定位精度的前提下，有利于整周模糊度的确定。因此组合观测值应满足长波长标准、弱电离层和弱观测噪声标准：长波长有利于模糊度的固定和提高模糊度解算成功率；弱电离层组合可以降低电离层延迟对组合观测值的影响；在组合观测值系数的选取过程中应使观测噪声尽量降低。

2.1波长标准

在双频和3频观测条件下，使用宽巷组合可以很容易地确定整周模糊度，以此为基础探讨BDS和Galileo具有长波长和弱电离层影响的4频组合观测值。

根据长波长的要求，使组合观测值的波长大于每个基本载波的波长。由式(11)得

(18)

可得不等式

λ1λ3λ4>iλ2λ3λ4+jλ1λ3λ4+kλ1λ2λ4+lλ1λ2λ3>0,

(19)

整理得

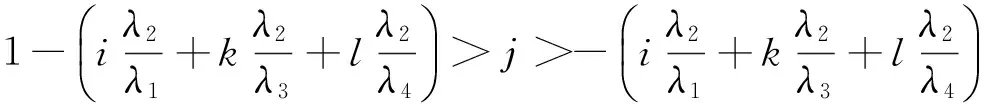
(20)

令

(21)

为保持j为整数，根据式(20)，取

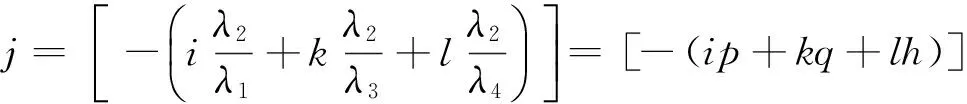
(22)

式中[(·)]为向+∞方向取整。结合式(11)得

(23)

由于p、q、h为整数的比值，因此式(23)为周期函数。i、k、l的周期分别为T1=T2=T3=T=115。考虑到组合观测值的观测噪声影响，可由式(17)降低组合观测值的观测噪声，应使i、j、k、l的绝对值尽量小；因此i、j、k、l的取值范围为

i∈[-57，58]，k∈[-57，58]，l∈[-57，58]；

(24)

并且i、j、k、l的取值不能同时为零。为了衡量组合观测值长波长这一特性，取λ和λ2的比值作为衡量指标。由波长和频率之间的关系可得

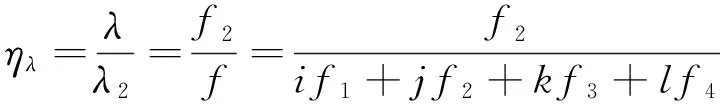
(25)

2.2弱电离层标准

由式(14)可得，组合观测值的电离层延迟为

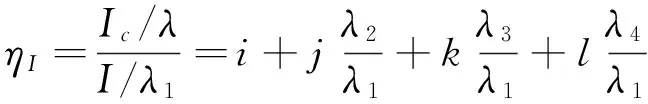
(26)

记

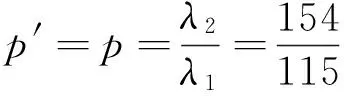
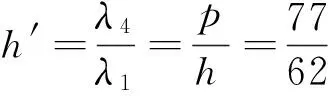
(27)

则式(26)可记为ηI=i+jp′+kq′+lh′。

若要使组合观测值的电离层延迟误差降低，应使比值ηI<1， 由式(26)可得

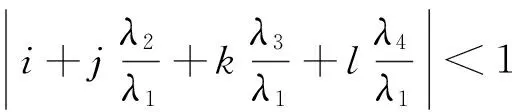
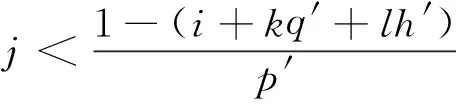
(28)

j的取值范围长度为

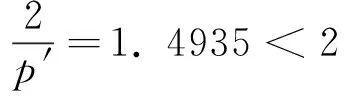
(29)

则j的可能取值有：

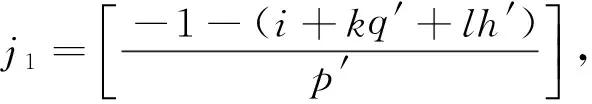
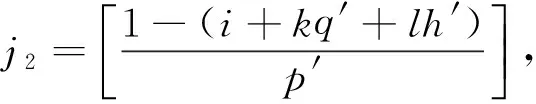
将j1和j2代入到式(23)可得：

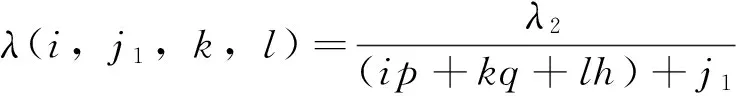
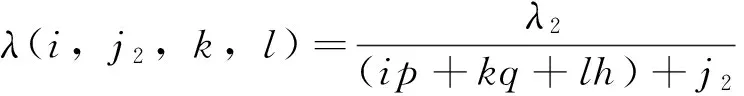
(30)

2.3组合观测值的选取与分析

由以上长波长系数的搜索范围及相关定义和公式，假设L1电离层延迟为1 m，可观测噪声如表1所示，可找出满足长波长要求和相对低噪声和弱电离层延迟的线性组合观测，如表2所示。

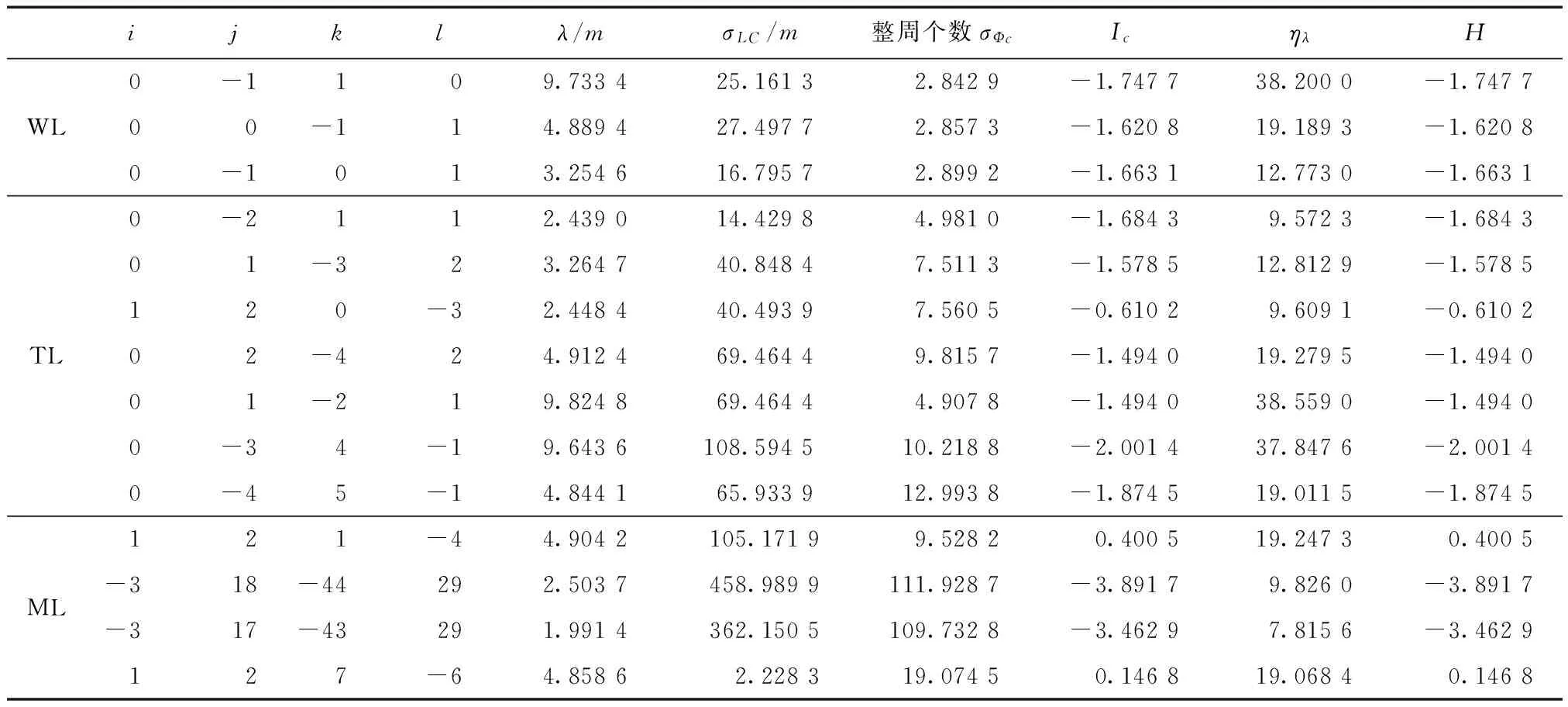
表2　典型的长波长及弱电离层组合观测值

表2中WL为传统意义上的宽巷组合，TL为典型的3频载波相位线性组合，ML为典型的多频载波相位线性组合；λ为组合观测值波长，σLc为假设L1噪声为1 m时的组合观测值的观测噪声，Ic为假设L1电离层延迟为1 m时的组合观测值电离层延迟，ηλ为组合观测值波长和L1波长的比值，H为组合观测值电离层延迟系数：它们是衡量组合观测值好坏的重要指标。

3结束语

长波长组合观测值的优势是使得整周模糊度更加容易确定。对于传统的宽巷组合虽然可以达到一定的波长；但电离层延迟仍然较高，电离层延迟系数H均大于1，相对单系统的宽巷组合没有明显优势，也没有突显出BDS和Galileo系统间组合的优势。对于2系统的3频载波相位线性组合，组合观测值(1，2，0，-3)具有长波长且组合噪声和电离层延迟系数均较小，分别为40.493 9和-0.610 2。在BDS和Galileo的4频相位组合中(1，2，1，-4)和(1，2，7，-6)的组合波长均大于4 m；并且电离层延迟小于0.5 m，远远低于波长的半周：是比较理想的多频组合。鉴于篇幅有限，本文只着眼于多频组合系数的选择方面，接下来会进一步检验利用此成果解算模糊度的可行性。

随着欧洲Galileo和BDS的建设，利用多频组合进行快速、高精度的载波相位定位的研究必将成为热点。

参考文献

[1]李克昭，孟福军，丁安民，等.BDS多频组合模糊度解算方法研究[J].河南理工大学学报：自然科学版，2015，34(1)：53-58.

[2]赵亮，叶世榕，陈德忠，等.组合观测值确定L1 & L2的模糊度的探讨[J].测绘地理信息，2013，38(2)：26-28.

[3]刘庆元，王潜心，龚佑兴.Galileo组合观测值的研究[J].测绘工程，2005，14(1)：15-16.

[4]李卫军，姜卫平，王泽民.GPS载波相位三频组合观测值的模型研究[J].测绘信息与工程，2008，33(3)：6-8.

[5]申俊飞，何海波，郭海荣，等.三频观测量线性组合在北斗导航中的应用[J].全球定位系统，2012，37(6)：37-40.

[6]杨霞，党亚民，成英燕.Galileo/GPS组合观测值模糊度解算方法研究[J].测绘科学，2009，34(2)：40-42.

[7]王泽民，柳景斌，伍岳，等.利用Galileo多个载波观测值解算整周模糊度的方法研究[J].测绘通报，2006(12)：1-4.

[8]WERNER W，WINKEL J.TCAR and MCAR options with Galileo and GPS[EB/OL].(2012-12-21)[2015-08-18].http：//navx-nsr.com/content/publications/2003/ION2003_Paper_TCARMCAR.pdf.

Optimal selection of BDS/Galileo phase combination observations

LI Kezhao1，2，ZHAO Leijie1，DING Anmin1，LI Zhiwei1，WEI Jinben1

(1.School of Surveying and Landing Information Engineering，Henan Polytechnic University，Henan Jiaozuo 454000，China；2.Collaborative Innovation Center of BDS Research Application，Zhengzhou 450052，China)

Abstract：Fast and correct integer ambiguity solution is limited by the wavelength and measurement noise in carrier phase measurement.Discussing on the issues，the paper came up with the idea that uses visual carrier phase combination observation of BDS/Galileo to increase the wavelength and keep low measurement nose.Under this condition，the ambiguity would be easily to be calculated.The principle of this method was elaborated in this paper.According to the selection criteria，the combination coefficient was selected and a few effective combination observations were got finally.The results showed that a few combination observations with specific properties could be obtained by using this method.

Keywords：BDS；Galileo；MCAR；ambiguity

收稿日期：2015-07-10

基金项目：国家自然科学基金项目(41202245，41272373)。

第一作者简介：李克昭(1977—)，男，甘肃靖远人，博士，副教授，研究方向为卫星定位/视觉导航的理论与应用。

中图分类号：P228

文献标志码：A

文章编号：2095-4999(2016)02-0071-04

引文格式：李克昭，赵磊杰，丁安民，等.BDS/Galileo相位组合观测值优化选取[J].导航定位学报，2016，4(2)：71-74.(LI Kezhao，ZHAO Leijie，DING Anmin，et al.Optimal selection of BDS/Galileo phase combination observations[J].Journal of Navigation and Positioning，2016，4(2)：71-74.)DOI：10.16547/j.cnki.10-1096.20160215.