关于正矩阵性质的几个不等式及Holder、Minkowski不等式的推广与发展

刘珍儒

(山东理工大学 理学院， 山东 淄博 255049)

关于正矩阵性质的几个不等式及Holder、Minkowski不等式的推广与发展

刘珍儒

(山东理工大学 理学院， 山东 淄博 255049)

摘要：推广得到了关于正矩阵性质的几个不等式，借此推广发展了经典的Holder、Minkowski不等式，并利用这些成果给出了恒正可积函数列的广义Holder及广义Minkowski积分不等式.

关键词：正矩阵； 矩阵的幂平均； 幂不等式

1基本概念

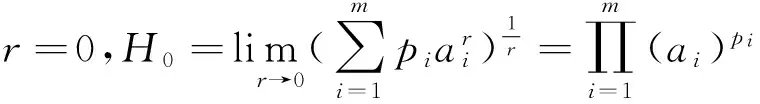
定义2设A为m×n阶矩阵.若A中各元素均为正数，即称A为正矩阵.本文中考虑的矩阵皆指正矩阵，不再重述.

矩阵各行(或各列)的平均系数，简称为行(或列)权系数.本文限定：同一矩阵各行取相同的行权系数，各列取相同的列权系数.

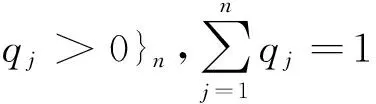
定义3对矩阵A各行的S次幂平均值，按矩阵A列权系数，作t次幂平均后的所得值，简称A的“行S次幂平均的列t次幂平均”.记为lt[Hs(A)].

类似，对A各列的t次幂平均值，按A的行权系数，作S次幂平均后所得值，简称矩阵A的“列t次幂平均的行S次幂平均”.记为Hs[lt(A)].

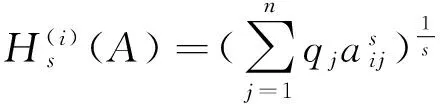
(1)

(2)

矩阵A的行算术平均的列几何平均，记为

矩阵A列几何平均的行算术平均.记为

矩阵A的行r次幂平均的列几何平均，记为

2有关正矩阵性质的几个不等式

定理1设A=(aij)m×n为正矩阵，则有

A的行算术平均的几何平均值≥其列几何平均的行算术平均.即L0[H1(A)]≥H1[L0(A)].亦即

(3)

定理2设A=(aij)m×n为正矩阵，r为非零实数，则

(i)若r>0时，有

(4)

即L0[Hr(A)]≥Hr[L0(A)]

(ii)r<0时，则不等式(4)反向，即

(5)

或Hr[L0(A)]≥L0[Hr(A)](r<0)

(6)

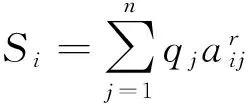
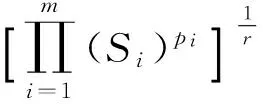
故

{Hr[L0(A)]/L0[Hr(A)]}r=

从而

推论1当r=1时，不等式(4)即为不等式(3).

证明设

令A1的行、列权系数分别为q1,q2,…，qn和p1,p2，…，pm,pm+1.

由不等式L0[Hr(A1)]≥Hr[L0(A1)]和L0[Hr(A)]≥Hr[L0(A)]所得不等式相同，且同为不等式(4).

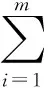
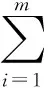
定理3设A=(aij)m×n为正矩阵，s、t为实数.

(i)若s>t>0，则有

(7)

即Lt[Hs(A)]≥Hs[Lt(A)].

(ii)若0>t>s,则有(7)式的反向不等式，即

(8)

即Hs[Lt(A)]≥Lt[Hs(A)].

证明利用矩阵A作矩阵Bk

其中，k=1，2，…,m，pi、pk为A的列权系数.

将不等式(3)用于矩阵Bk，则有

L0[H1(BK)]≥H1[L0(BK)]

(9)

而

L0[H1(BK)]=

H1[L0(BK)]=

将以上两式代入(9)式两端，即得

(10)

在不等式(10)两边，分别关于k从1至m作和，化简后则有

(11)

(12)

在(12)式两边同作1/t将乘幂(只取正主值)

(1)当s>t>0时，因1/t>0,则(7)成立.

(2)当0>t>s时，因1/t<0,故1/t将乘幂后，不等式反向，则(8)成立.

即Hs[Lt(A)]≥Lt[Hs(A)](0>t>s)

证讫.

顺便指出：不等式(4) 与(5)和不等式(7)与(8)都分别是同一不等式参数的分段表示.

不等式(或等式)两边取同极限所得不等式(或等式)，简称为原不等式(或等式)的极限形式.

定理4(i)不等式(4)是不等式(7)中S=r，当t→0+时的极限形式.

(ii)不等式(5)是不等式(8)中s=r，当t→0-时的极限形式.

证明(i)、令s=r,t→0+，在不等式(7)两边同取极限，即

(13)

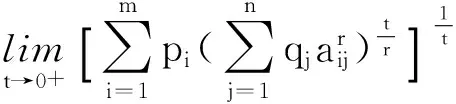
(14)

(15)

将(14)、(15)代入(13)式，得(4)成立.即不等式(4)是不等式(7)的极限形式.

同法可证(ii).

3广义Holder与Minkowski积分不等式

令{fi(x)}m表示函数列f1(x),f2(x),…，fm(x).

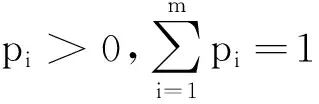
(1)若r>0，有

(16)

即函数列{fi(x)}m的r次积分幂平均的几何平均≥函数列{fi(x)}m的几何平均的r次积分幂平均.

(2)设s、t为实数，若s>t>0，则有

(17)

即函数列{fi(x)}m的S次积分幂平均的t次幂平均≥函数列{fi(x)}m的t次幂平均的S次积分幂平均.

若0>t>s，则有

(18)

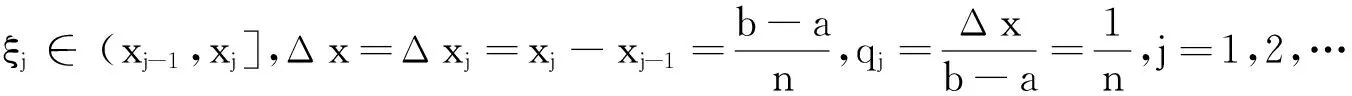
(19)

令n→+∞,即Δx→0,在(19)两边同取极限，即

由根据极限性质，即有

利用定积分定义，即得

(20)

推论3(1)令(20)式中r=1,则有

(21)

即{fi(x)}m积分的几何平均≥{fi(x)}m几何平均的积分.

(2)令(17)中S=r，t=1，即得

(22)

即函数列{fi(x)}m的r次积分幂平均的算术平均≥函数列{fi(x)}的算术平均的r次积分幂平均.

(3)令(17)式中S=1，t=r，即有

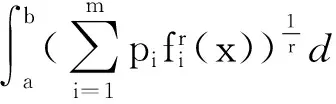
(23)

下例证明了幂平均和积分幂平均的重要性质.

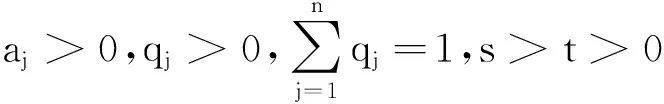
(s>t>0)

(24)

(s>t>0)

(25)

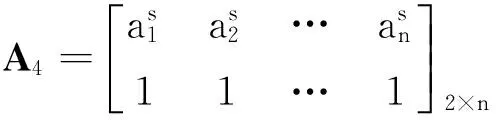
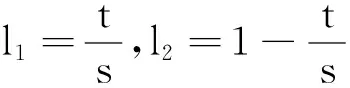
将不等式(3)用于矩阵A4，则L0[H1(A4)]≥H1[L0(A4)]化为

化简得

参考文献:

[1]刘珍儒.正矩阵的一个性质及其应用[J].工程数学学报,1988,15(2):113-116.

[2]刘珍儒.关于几类平均的几个不等式[J].工程数学学报,2003,20(4):90-96.

[3]史济怀.平均[M].北京：人民教育出版社，1964.

[4]《数学手册》编写组.数学手册[M].北京：人民教育出版社,1979.

(编辑：刘宝江)

Several inequalities on properties of positive matrix and the extension for Holder,Minkowski inequalities

LIU Zhen-ru

(School of Science, Shandong University of Technology, Zibo 255049, China)

Abstract:This paper obtained several inequalities on the nature of the positive matrix, thereby promoting the classical Holder and Minkowski inequality, it gives the generalized Holder-Minkowski integral inequality for Hengzheng integrable function

Key words:positive matrix; matrix power means; power inequality

收稿日期：2015-03-08

作者简介：刘珍儒，男，liuqiang335@sina.com

文章编号：1672-6197(2016)05-0069-05