基于AIC的组合预测方法在地区GDP预测中的应用

苑慧芳， 林　鹏

(山东理工大学 理学院， 山东 淄博 255049)

基于AIC的组合预测方法在地区GDP预测中的应用

苑慧芳， 林鹏

(山东理工大学 理学院， 山东 淄博 255049)

摘要：在经济管理领域中，自回归移动平均模型有着广泛的应用，组合预测可以有效提高模型的预测效果，尤其在实证分析中，模型在各时期的特性并不保持完全一致，更表明了组合预测的必要性，因此如何设置权重，进行有效的组合预测便成为了关注的问题.提出了一种基于赤池信息量准则(AIC)设置权重，进行向前一步组合预测的方法，采用拟合误差指标作为预测方法优劣的评判标准，与传统预测方法及常用组合预测方法做出对比，对预测效果进行全方位的综合性评价，并运用实例说明基于AIC的组合预测方法的优越性.

关键词：自回归移动平均模型； 赤池信息准则； 组合预测； 拟合误差指标

自回归移动平均(ARMA)模型是常用的时间序列模型，在经济管理、工程技术等领域有着广泛的应用，特别是短期预测效果较好.在运用ARMA模型进行预测时，首先应该判断一组随机变量序列或者通过一系列变换后的随机变量序列是否适合建立时间序列模型.如果不适合建立时间序列模型，可以选择其他的建模方法进行预测.如果能够建立时间序列模型，可以通过模型识别、参数估计、诊断检验等步骤确定几个候选模型，再分别对候选模型进行普通预测和不同方式的组合预测，通过拟合误差的指标来对比不同方法的组合预测的效果与普通预测的效果，从而综合评价各方法的优劣.

赤池信息准则(AIC)是赤池弘次(H.Akaike)在研究信息论特别在解决时间序列定阶问题中提出来的，作为模型定阶的一种准则，此准则在组合预测中，对于权重的设置起到至关重要的作用.对于实证研究，本文将利用山东省1975-2013年地区生产总值数据(保留2014年真实的地区生产总值)建立适当的模型，对2014年地区生产总值进行预测，进一步说明基于AIC的组合预测过程及其优越性.

1预测方法

对于时间序列模型，普通的预测方法是根据最佳线性预测性质，以条件期望代替预测值，而组合预测方法则是根据设置的权重对候选模型加权平均.

1.1一般预测方法

针对ARMA模型，以及求和的ARIMA模型均可根据最佳线性预测的性质用条件期望代替预测值进行模型预测.

1.1.1ARMA(p,d,q)模型的预测

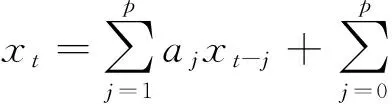
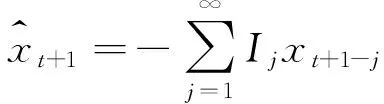
1.1.2ARIMA(p,d,q)模型的预测

A(β)(1-β)dxt=B(β)εt,εt～WN(0,σ2),t∈Ν,

则yt=(1-β)dxt,t=d+1,d+2,…,n,满足ARMA(p,q)模型.

1.2组合预测方法

组合预测方法是根据各候选模型的预测值适当的加权平均，用以提高模型预测效果所做的预测方法，其核心是各候选模型权重的设置.

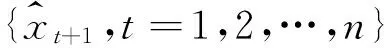
一般情况下，按权重设置方法不同，组合预测方法会分为固定权重系数组合预测法和变权系数组合预测法两大类.对于固定权重系数组合预测法，权重通常根据候选模型的个数确定；对于变权系数组合预测法，权重通常会根据模型预测误差的标准差、模型误差平方和、模型预测方差等指标来确定.

1.2.1固定权重系数组合预测法

此方法主要根据候选模型的个数来确定权重，各候选模型的权重[3]为

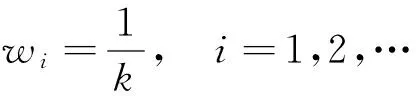
1.2.2变权系数组合预测法

(1)标准差优选组合预测法

权重通常根据模型预测误差的标准差来设置，各模型的权重[4]为

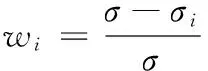
其中σi表示候选模型mi的预测误差的的标准差.

(2)残差倒数法

权重通常根据模型误差平方和来设置，各模型的权重[5]为

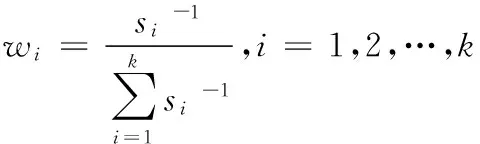
其中si表示候选模型mi的误差平方和.

(3)方差倒数法

权重通常根据模型的预测方差来设置，各模型的权重[3]为

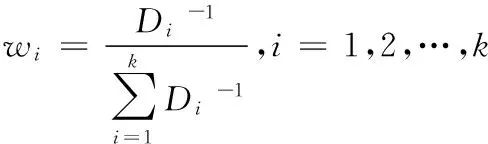
其中Di表示候选模型mi的预测方差.

(4)基于AIC的组合预测法

①权重通常根据模型的AIC值来设置，各模型的权重[6]为

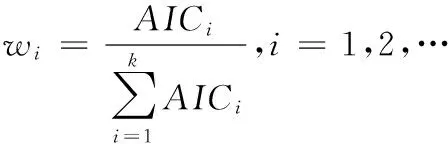
②权重通常根据模型的AICi/2值来设置，各模型的权重[6]为

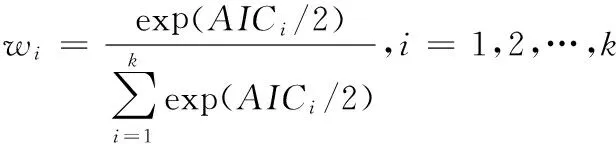
其中AICi表示候选模型mi的AIC值.

2模型预测优劣的判定方法

当存在多种侯选模型时，普通预测的结果往往与组合预测的结果有一定的差异，至于哪种预测方法有较好的预测效果，往往会通过拟合误差指标[7-8]来判断预测效果的优劣.

(4)平均绝对百分比误差

(5)均方百分比误差

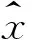
以上五种指标越小说明候选模型预测效果越好.

(6)预测的有效度

预测有效度[9]作为模型优劣的主要判别指标，即对预测精度进行加权平均的一种指标.

①预测相对误差

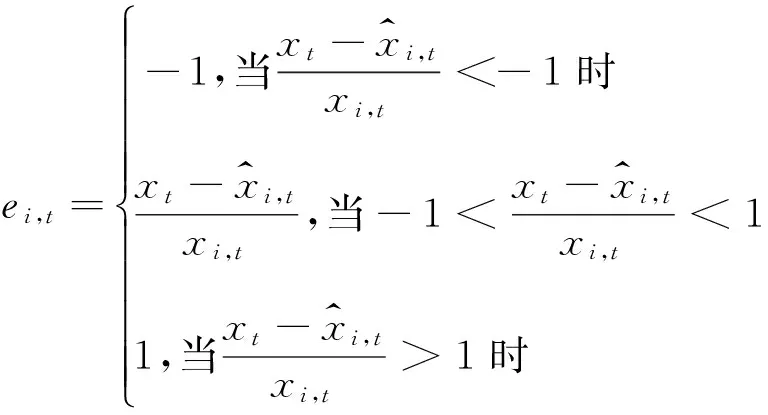
②预测精度

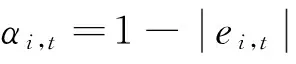
③预测有效度

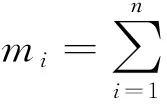
3实例分析

以山东省1975年-2014年地区生产总值[9]建立时间序列模型，基于AIC准则，进行组合预测，本文只采用了1975年-2013年的数据，保留2014年的地区生产总值(53426.9亿元)，借助于Eviews软件建立合适的模型，预测2014年的地区生产总值，并根据预测误差指标对比不同组合预测方法与普通预测方法的预测效果.

3.1平稳性检验

平稳性检验是时间序列模型预测的基础，有时序列并非平稳，就需要对序列进行一系列的变换，使之成为平稳序列，再进行建模.有关数据录入及平稳性检验过程可分以下几步完成.

(1)将山东省1975年-2014年地区生产总值(单位：亿元)记为序列{xt}，其中t为年份，且t=1975,1976…2013.并将数据录入软件，作时序图，初步观察序列的平稳性，通过观察{xt}的时序图(图1)，可知该序列呈现指数趋势变动，显然序列是不平稳的，

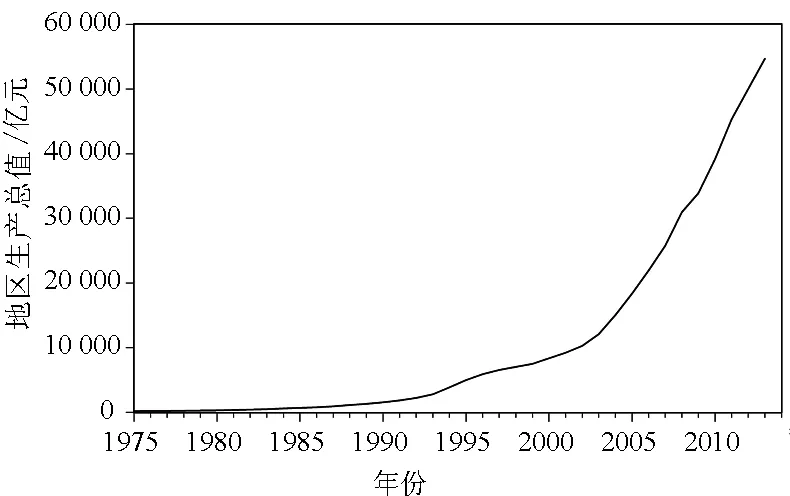
图1　山东省1975年-2013年地区生产总值{xt}的时序图

(2)为使序列趋于平稳，首先将其对数化处理，记对数化后的序列为{log(x)t,t=1975,1976,…,2013}，由{log(x)t}的时序图(图2)，可知对数化的序列呈线性上升趋势，故可对其进行差分运算，转化为平稳时间序列.

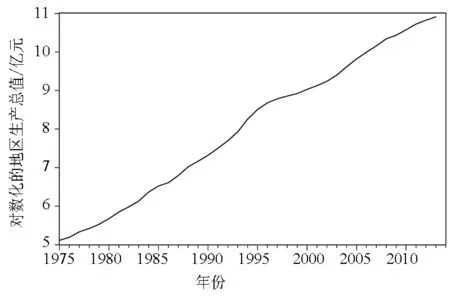
图2　对数化的地区生产总值{log(x)t}的时序图

(3)对序列{log(x)t}进行差分运算，记一阶差分后的序列为{yt,t=1975,1976,…,2013}，二阶差分后的序列为{zt,t=1975,1976,…,2013}，一般若差分后的序列值在0±0.5之间变动时，可认为序列平稳，而一阶差分与二阶差分后的序列值均在此范围内，故可进一步通过ADF检验判断序列的平稳性，见表1.

表1 ADF检验统计量表

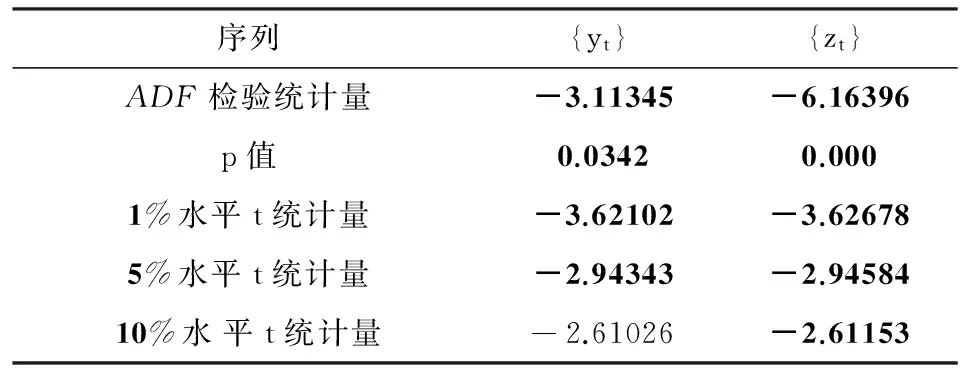
序列{yt}{zt}ADF检验统计量-3.11345-6.16396p值0.03420.0001%水平t统计量-3.62102-3.626785%水平t统计量-2.94343-2.9458410%水平t统计量-2.61026-2.61153

由ADF检验结果可知在显著水平为0.01的条件下，二阶差分后的序列拒绝存在单位根的原假设，即此序列是平稳的.

3.2模型识别

由于序列{zt}的自相关-偏自相关图可知偏自相关系数在5阶之后是明显截尾的，而自相关系数在滞后2阶、5阶和10阶时落在2倍的标准差的边缘，有待于进行模型选择.由自相关-偏自相关系数，可对{zt}尝试建立几种不同的模型拟合，如ARMA(5,2),ARMA(5,3) ,ARMA(5,4)等，通过模型系数显著性(若统计量的P值小于显著水平0.05，则认为系数在此水平下是显著的)检验初步认为以下几种模型比较适合，模型的一些统计指标见表2.

3.3模型诊断检验

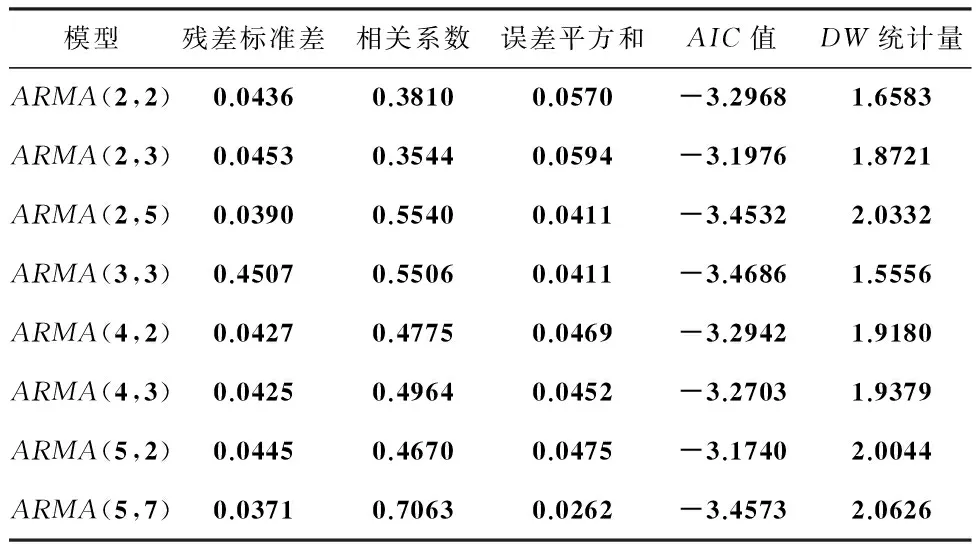
模型诊断性检验实际是检验残差序列是否为平稳的白噪声序列，若DW统计量在2附近，残差不存在一阶自相关，而ARMA(2,2)模型与ARMA(3,3)模型DW统计量明显小于2，故不能作为候选模型，还需要对残差做进一步分析，即通过自相关与偏自相关图检验，通过观察自相关与偏自相关系数图可知ARMA(2,3)模型残差存在自相关，也不能作为候选模型，因此候选模型共有5个，分别是ARMA(2,5)模型，ARMA(4,2)模型，ARMA(4,3)模型，ARMA(5,2)模型，ARMA(5,7)模型.其中ARMA(5,7)模型相关系数最大，相对而言，可初步认为ARMA(5,7)模型拟合效果最好，具体判断还要根据模型优劣判别的几项指标，ARMA(5,7)模型拟合效果图如图3所示.

表2各候选模型部分指标值表

模型残差标准差相关系数误差平方和AIC值DW统计量ARMA(2,2)0.04360.38100.0570-3.29681.6583ARMA(2,3)0.04530.35440.0594-3.19761.8721ARMA(2,5)0.03900.55400.0411-3.45322.0332ARMA(3,3)0.45070.55060.0411-3.46861.5556ARMA(4,2)0.04270.47750.0469-3.29421.9180ARMA(4,3)0.04250.49640.0452-3.27031.9379ARMA(5,2)0.04450.46700.0475-3.17402.0044ARMA(5,7)0.03710.70630.0262-3.45732.0626

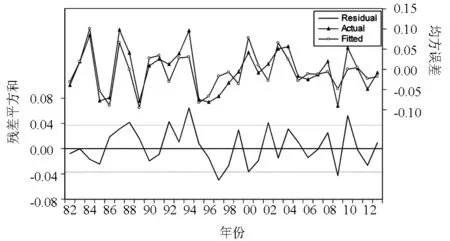
图3　ARMA(5,7)模型拟合效果图

3.4模型预测及预测效果的比较

所谓模型预测，即在确立了候选模型后，根据往期的数据来预测未来某一期或是某几期的数据，在普通的预测方法的基础上，还会尝试多种组合预测方法，然后运用拟合误差指标比较普通预测方法与组合预测方法的优劣.

3.4.1各单项候选模型普通预测方法效果比较

Eviews软件中采用一般的模型预测方法，以条件期望来代替预测值，而序列{log(x)t}经过二阶差分后为自回归移动平均模型，故{log(x)t}为ARIMA(p,d,q)模型，其中d为2，由模型诊断性检验，对于序列{log(x)t}可得候选模型：ARIMA(2,2,5)模型，ARIMA(4,2,2)模型，ARIMA(4,2,3)模型，ARIMA(5,2,2)模型和ARIMA(5,2,7)模型.由1.1.2节涉及的公式及运行结果，可通过模型的误差拟合指标对比这五种候选模型的预测效果见表3.

表3候选模型的普通预测方法所得误差拟合指标

候选模型拟合指标ARIMA(2,2,5)ARIMA(4,2,2)ARIMA(4,2,3)ARIMA(5,2,2)ARIMA(5,2,7)SSE8804926938380617724168805248160377679713174877248121301MAE46360.6145503.2045436.4845029.8045109.71MSE8242.538350.968346.157702.878422.29MAPE42.9032.1732.1927.8327.79MSPE12.799.669.698.448.41预测有效度0.1158639010.1227476620.1232294080.1268307380.126840115

其中ARIMA(5,2,7)模型与ARIMA(5,2,2)模型的各拟合误差指标相对于其他单项候选模型而言较小，而ARIMA(5,2,7)模型SSE、MAE、MSE比ARIMA(5,2,2)模型小，ARIMA(5,2,7)模型MAPE、MSPE比ARIMA(5,2,2)模型大，通过这几个普通的模型优劣判别指标难以判断这两个模型哪个模型是最好的，故可通过预测有效度进一步判断模型的预测效果，ARIMA(5,2,7)模型预测有效度预测有效度最大，可认为ARIMA(5,2,7)模型相对于其他几个候选模型是最好的，这与前面模型诊断性检验中的初步结论相吻合.

3.4.2基于AIC的组合预测方法与其他组合预测方法效果比较

近年来，组合预测方法广泛应用于短期经济预测中，可以有效减少预测的系统误差，改进预测效果，基于AIC的组合预测方法效果，同样也要通过一些拟合误差指标来衡量，见如表4.

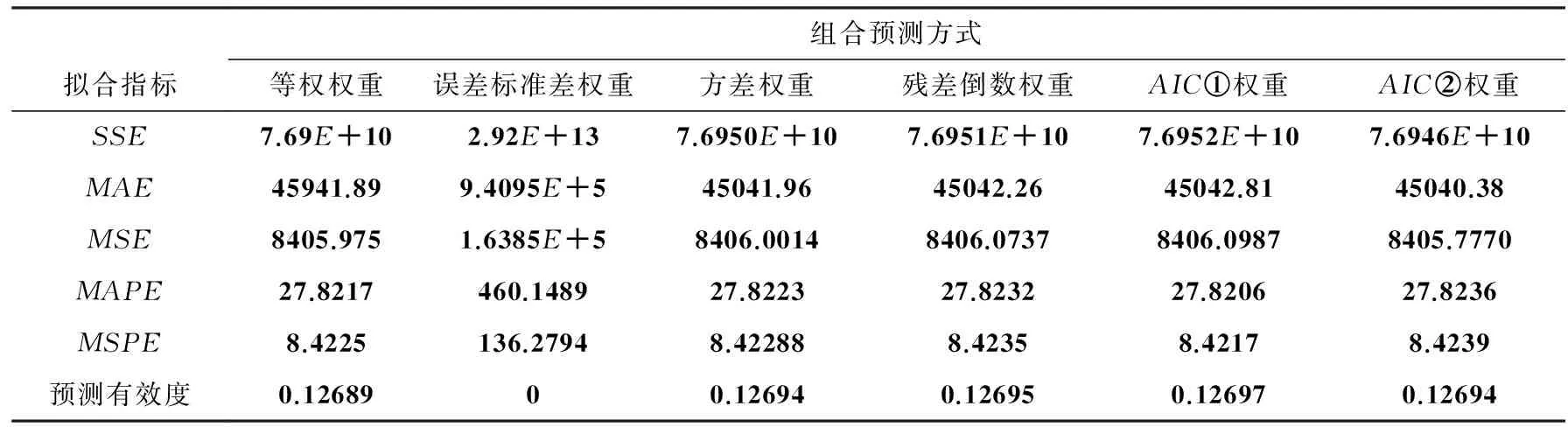
表4各组合预测方法所得模型拟合误差指标

组合预测方式拟合指标等权权重误差标准差权重方差权重残差倒数权重AIC①权重AIC②权重SSE7.69E+102.92E+137.6950E+107.6951E+107.6952E+107.6946E+10MAE45941.899.4095E+545041.9645042.2645042.8145040.38MSE8405.9751.6385E+58406.00148406.07378406.09878405.7770MAPE27.8217460.148927.822327.823227.820627.8236MSPE8.4225136.27948.422888.42358.42178.4239预测有效度0.1268900.126940.126950.126970.12694

通过各组合模型预测方法的指标与ARIMA(5,2,7)模型的指标对比，发现误差标准差权重组合预测方法效果最差，甚至还不如普通的候选模型预测方法；其他的组合预测方法比普通的预测方法有所改进，预测有效度由高到低分别为基于AIC所做的组合预测法、残差倒数权重组合预测法、方差权重组合预测法、等权权重组合预测法，其中两种基于AIC所做的组合预测法中，第①种方法预测有效度较大，而且要比残差倒数权重组合预测法的预测有效度大，相对而言，基于AIC所做的组合预测法是比较好的.

4结束语

模型的组合预测方法是对传统预测方法的一种推广，在一定程度上虽然可以提高预测的效果，极大限度利用预测样本的信息，但是自身存在一定的局限性，比较适用于短期的时间序列预测模型.并非所有的平稳序列都可以做组合预测，要根据实际情况而确定，如果候选模型的预测效果远远优于组合预测的效果，那么组合预测也就失去了优越性，就需要寻找其他的方法来提高预测有效度.而无论采用何种新的方法进行预测，都要根据模型优劣判别指标如SSE、MSE、MSPE、预测有效度等来验证预测效果是否得到改进，进而确定是否要采用新的方法进行预测。基于AIC的组合预测方法，虽然在一定程度上提高了预测效果，但是相对于某些预测方法来说并非最优，实际中也要不断的尝试新的方法来改进预测效果，最终找到合适的方法进行预测.

参考文献:

[1]何书元. 应用时间序列分析[M]. 北京: 北京大学出版社, 2003:169-183.

[2]肖枝洪，郭明月. 时间序列分析与SAS应用[M]. 2版. 武汉: 武汉大学出版社, 2012：95-103.

[3]门小琳. 组合预测方法在我国CPI预测中的应用[D]. 南京: 南京财经大学，2012.

[4]杨广喜. 经济预测中组合预测法的应用[J]. 统计与决策, 1998(6): 17-20.

[5]詹英. 组合预测方法在我国人均GDP预测中的应用[D]. 武汉:华中师范大学，2014.

[6]BucklandST,BurnhamKP,AugustinNH.Modelselection:anintegralpartofinference[J].BIOMETRICS,1997,53(7):603-617.

[7]王金山，杨国超. 一种基于时序可变加权系数的组合预测模型[J]. 自然科学, 2012,26(2):120-121.

[8]陈华友. 组合预测方法有效性理论及其应用[M].北京：科学出版社，2008:150-240.

[9]中国国家统计局.中国统计年鉴[M].北京：中国统计出版社，2014.

(编辑：刘宝江)

The application of forecast combination based on AIC in the regional GDP

YUAN Hui-fang, Lin Peng

(School of Science, Shangdong University of Technology, Zibo 255049, China)

Abstract:In the sphere of economic and management, ARMA model(the auto-regressive and moving average model) has been widely used. Forecast combination can effectively improve the results of prediction, so how to use them has became our concern. In this paper, we can use the methods of combined forecast to set weight based on the Akaike Criterion (AIC). Using fitting error indicators as criteria to make a comparison of the predicted effects, so we can make a full range of comprehensive evaluation, and use examples to illustrate the superiority of forecast combination.

Key words:ARMA model； AIC; forecast combination； fitting error indicators

收稿日期：2015-08-04

作者简介：苑慧芳,女,tongjiyuanhuifang@126.com; 通信作者： 林鹏,男,mathlinpeng@163.com

文章编号：1672-6197(2016)05-0064-05

中图分类号：O211.61

文献标志码：A