一道练习题的教学实践和反思

陈平

[摘 要]课堂教学中，教师应充分考虑学生的认知基础，引导学生经历知识产生、发展、形成的过程，并通过问题引发学生的思考，使学生获得知识的同时，发展思维能力，感悟数学思想，积累基本的数学活动经验。

[关键词]过程 思维 活动经验 规律

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）17-031

案例回放：

苏教版小学数学五年级下册第七单元“解决问题的策略”第二课时中有这样一道习题，如下图。

在解决这道题时，我先让学生数出铅笔架中每一层铅笔的支数以及层数，引导学生列出算式6+7+8+9+10+11+12+13+14+15，然后让他们尝试计算。学生通过题中的提示“你能联系梯形面积公式”以及观察图形，很顺利地找到了计算的方法。方法如下：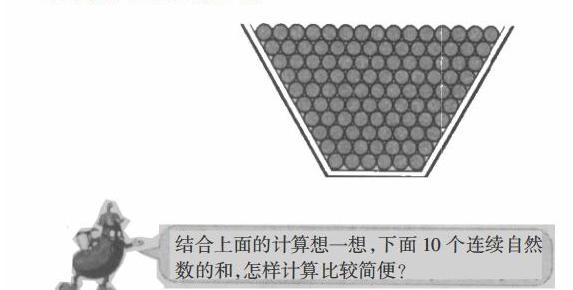

方法1：6+7+8+9+10+11+12+13+14+15

=（6+15）×10÷2

=21×10÷2

=210÷2

=105（支）

方法2：6+7+8+9+10+11+12+13+14+15

=（6+15）×（10÷2）

=21×5

=105（支）

对后续练习中的类似题目，大多数学生能用上述方法列式求和。一节课就这样顺利地结束了，我觉得学生已经掌握了这两种方法，但是第二天学生的作业情况却让我大吃一惊：五道这样的求和题目，全班只有七个人是完全解答正确的。我不禁反思到底是什么地方出了问题。

回忆上节课的教学过程，由于缺乏必要的数学活动，学生没有进行观察、比较、分析、抽象、概括等活动，没有经历知识发生、发展及形成的过程，因而他们并没有真正理解和掌握这两种方法。针对上述问题，我再次进行如下的教学实践。

片断一：

（投影出示五道题目，如下）

（1）2+3+4+5+6+7+8 （2）16+14+12+10+8+6

（3）1+3+5+7+9+11+13 （4）17+19+21+23+25+27

（5）2+6+10+14+18+22

师：你能用昨天学过的方法求出这些算式的和吗？

①学生独立完成。

②师指名学生上台板演，有不同方法的学生可以进行补充。

……

③组织学生评价，每道题都板书上述两种解法。

片断二：

师：仔细观察这五道题目，它们有什么相同点和不同点？

生1：都是加法运算。

生2：我觉得第（2）题和其余四题不一样，它的数字越来越小，其他四题的数字越来越大。

生3：我发现这五道题中数字的排列都是有规律的，如第（1）题前后两个数的差是1，第（2）、第（3）、第（4）题前后两个数的差是2，第（5）题前后两个数的差是4。

生4：一句话就可以说清楚了，即每道题中相邻两个数之间的差是一样的。（其他学生都表示同意生4的观点，师再请一位学生说一说）

师：那你们能根据这样的规律，编出具有这种规律的题目吗？先自己想一想，然后在小组里交流一下自己的想法。

①学生先独立思考，然后小组交流。

②师组织学生交流，择机板书以下两道算式。

1+5+9+13+17+21+25+29

40+35+30+25+20+15+10+5

……

片断三：

师：认真观察上述我们刚刚完成的五道题，它们的计算方法有什么共同点？

生5：计算的形式是一样的，都是几加几的和乘几再除以2，或者是几加几的和乘几除以2。（师按照学生说的把同一形式的方法分别圈起来）

生6：几加几就是每道题的第一个数加上最后一个数。

……

师：那你们能用一个式子表示刚才的计算方法吗？

生7：（第一个数+最后一个数）×个数÷2=和。

生8：（第一个数+最后一个数）×（个数÷2）=和。

……

片断四：

师（出示2+3+5+9+15+18+21+23）：这道题你打算怎么算？

生9（脱口而出）：（2+23）×（8÷2）。

生10：不对。因为相邻两个数的差不一样，所以不可以用这种方法算。

生11：8个数分成4组，每组的和是不一样的，所以不可以这样算。

师：回顾刚才我们总结的计算方法，它的前提条件是什么？

生12：相邻两个数的差要一样。

……

反思：

1.教师的教是为了学生更好的学

教师应尊重学生已有的生活经验和认知起点，把握学生的“最近发展区”，并充分利用学生已有的知识经验，帮助他们构建已有知识经验和目标结果之间的桥梁，促进学生不断完善自己的认知结构。如在“简易方程”这一单元中，有一道习题是研究3个连续自然数之和与中间数的关系。在教学中，我曾引导学生归纳总结得出“求奇数个连续自然数的和可以转化为中间数乘个数”，这个已学的知识点是学生这节课进一步学习的知识基础。教学这节课时，如能在复习该知识点之后，再组织学生进行前面所提到的探究活动，定能激发学生探究的欲望，引导学生积极主动地参与到学习中来，从而提高课堂教学的有效性。

2.数学教学不应只是指向结果的教学，而应是重视过程的教学

课堂教学中，教师应创造机会引导学生经历知识产生、形成的过程，使学生真正理解所学知识。如上述教学中，我先通过一组题目让学生观察、比较，发现它们共同的特征，再让学生观察、比较题目的解题方法的共同点，进而引导学生抽象、概括出解决此类问题的策略。整个教学过程，学生全身心地投入，积极思考，思维不断发生碰撞，最后归纳总结出正确的结论。这里更为重要的，引导学生经历了观察、比较、抽象、概括等数学活动的过程，发展了学生的思维，提升了学生的学习能力，使学生获得了解决此类问题的策略。同时，让学生感悟到学习过程中蕴含的“变与不变”“数学模型”等数学思想，积累了丰富的数学活动经验。

（责编 杜 华）