熵权-集对分析方法在大坝运行风险评价中的应用

吴胜文，秦　鹏,，高　健，闫潇群

(1.浙江水利水电学院 水利与环境工程学院，杭州　310018；2.河海大学 水利水电学院，南京　210098)

熵权-集对分析方法在大坝运行风险评价中的应用

吴胜文1，秦鹏1,2，高健1，闫潇群2

(1.浙江水利水电学院 水利与环境工程学院，杭州310018；2.河海大学 水利水电学院，南京210098)

摘要：根据大坝实际运行状况，确立恰当的评价指标和评价准则并对大坝运行风险状况做出准确的判断，是水利工程运行管理的重要内容。然而，评价指标和评价准则之间往往存在复杂的模糊、非线性关系。集对分析法在定量处理多因素间不确定性问题上有较大的优越性，可以用来进行大坝运行风险的评价。采用信息论中的熵权理论，通过定量计算各指标所提供的信息量的大小来确定指标权重，建立基于熵权的大坝运行风险评价集对分析模型，将该模型应用于某坝运行风险评价中，计算分析得出该坝安全等级，并预测其风险发展的趋势。实例证明，基于熵权的集对分析方法简单可行、科学合理，为大坝运行和风险评价提供了新的方法。

关键词：大坝；运行安全；风险评价；信息熵；集对分析

1研究背景

我国水能资源非常丰富，目前已建成98 000多座水库大坝，其安全运行是维护下游人民群众生命财产安全和促进社会经济可持续发展的重要保障[1]。大坝运行风险评价是掌握大坝运行结构性态、保障大坝安全的重要手段。考虑到建坝条件、设计施工质量、极端气候、运行管理等因素的影响，大坝在不同程度上均存在安全隐患和失事风险。因此，有必要对现役大坝进行运行期风险评价，了解大坝所处的风险状况，及时发现潜在安全隐患，并依据评价结果采取相应的措施，保障大坝的安全运行，降低溃坝风险[2]。目前，关于大坝运行期风险评价方法的研究已经取得了一定进展，马福恒[3]基于诺埃曼风险率模型对可能失事的病害模式进行识别，提出了一种大坝风险率定性和定量相结合的确定方法；李晓璐等[4]综合应用层次分析法和模糊数学理论，提出了基于多层次模糊分析法的大坝安全评价模型；杨灿等[5]提出了基于原型监测资料的重力坝运行风险评价方法。然而，影响大坝运行安全的因素复杂繁多，如何更加客观真实地评价大坝运行风险进而对其进行风险预警，仍然是大坝安全管理过程中亟待解决的问题[6-7]。考虑到集对分析法在定量处理多因素间不确定性关系方面的优越性，将其引入到大坝运行风险评价中，并结合信息熵理论，建立了基于熵权的大坝运行风险评价集对分析模型，并开展应用研究。

2大坝运行风险评价指标体系及度量

目前，我国大坝运行风险评价方法和手段主要借助于大坝安全评价相关理论。传统的大坝安全评价是以大坝工程安全为核心，对有关工程安全的若干专题进行研究，判定各专题的安全程度，其目的是评价工程是否安全，属于哪一类坝[8]。《水库大坝安全评价导则》[9]中，将大坝风险因素划分为7个方面，包括运行管理、工程质量、防洪安全、结构安全、渗流安全、金属结构安全、抗震安全，同时将每个方面的安全状况分为A，B，C 3个等级。A级为安全可靠；B级为基本安全，但部分有缺陷；C级为不安全。同时，综合各专项安全性级别对大坝进行分类：各方面安全级别均达到A级的，为一类坝；安全级别均为B级及以上的，为二类坝；安全性级别中有1项以上(含1项)为C级的，为三类坝。

然而，实际工程表明，将大坝的运行期风险状况粗略地分为A，B，C 3个等级并不能满足大坝运行期风险状况评判的需要。为了更加客观准确地反映大坝运行安全风险状况，将不安全的状况即等级C进一步细化为不安全、很不安全、极不安全3种情况。因此，大坝的安全状况可分为5级：安全、基本安全、不安全、很不安全、极不安全；对应的安全风险程度分别为：无病险、一般性病险、较重大病险、严重病险和极严重病险[8-9]。为了准确地评估运行期大坝所处风险状态，并给专家提供足够的空间以便准确地细分和量度，根据文献[8]对区间[0,1]进行等分，以此作为评判标准，将定性判断转化为定量评价，如表1所示。

表1　大坝安全和风险状态分级及定量描述

3基于熵权-集对分析的大坝运行期风险评价模型

3.1集对分析原理

集对分析理论[10]由我国学者赵克勤于1989年提出，该理论可以定量处理随机、模糊以及不确定性等问题，其实质是将所研究问题的确定、不确定性视作一个系统，该系统用“同一”和“对立”2个特征来描述确定性，并用“差异”来描述系统中的不确定性，从同、异、反3个方面对目标系统进行分析。集对，是指由有一定联系的两集合构成的对子。一般地，如果具有某种联系的集合X和集合Y都包含N个方面的特性，即X= (X1，X2，…，XN)，Y= (Y1，Y2，…，YN)，则用H=(X,Y)表示集合X和Y构成的集对。利用不确定性系统中相互关联的2个集合构造集对，进而对该集对某一特定属性进行同一性、对立性、差异性分析，并用联系度来表征集对之间的同、异、反关系。

集对分析理论的基本思路是[11-12]：具体问题背景下，对集对H的特性进行分析，共得到N个特性，其中包括S个共有的特性、P个对立的特性以及F个既非共有又非对立的特性，由此建立集合X和集合Y在指定问题背景下的联系度，即

(1)

式中：μ为集对H的联系度；S为共有特性个数；P为对立特性个数；F为差异特性个数；i为差异不确定性系数，且i∈[-1,1]，也可仅起差异标记作用；j=-1为对立度系数，有时仅起标记作用，N=S+F+P。

因此，可以通过集对分析理论对常见的不确定现象如随机、模糊等进行描述。其中，联系度μ和不确定系数i的确定是运用该理论处理此类问题的关键。

多元联系数是根据联系度函数μ在bi项上的展开。以五元联系数为例，将其记为

(2)

式中，a+b+c+d+e=1，i1∈[0,1]，i2为中性标记，i2= 0，i3∈[-1,0]，j=-1。多元联系数和同异反三元联系数可以根据需要进行转换，由于多元联系数在处理多因素多层次问题中具有一定的优势，在实际研究中得到了广泛的应用。

3.2熵值法确定指标权重

熵是信息论中反映系统无序度的一种度量，信息熵越大，表示信息的无序程度越高，其效用值越小。熵权法是计算综合指标权重的一种数学方法，其优势在于可以综合考虑各因素所提供的信息量。熵权法的实质是通过定量计算各指标所提供的信息量的大小来确定指标权重，若某项指标所提供的信息量较大，则说明该指标权重较大。通常采用熵值作为信息量大小的度量。进行评价时，对于同一指标，往往有若干评价值，如果这些值之间相差越大，说明该指标值的选取对于评价结果有重要的影响，因此该指标提供的有效信息量也就越大，计算出的熵值就越小。如果这些值完全相同，此时熵值达到最大，这意味着该指标值的选取对于评价结果没有影响，可以考虑将其从评价指标体系中去除[13-14]。

熵权法依据评价指标构造的判断矩阵来确定权重，消除了各因素权重的主观性，更加有利于得到符合客观实际的评价结果[15]。

3.3基于熵权-集对分析的大坝运行风险评价模型

3.3.1联系度确定

联系度是集对中两集合关系的量化，能定量地显示两集合之间的复杂关系[16]。基于集对分析理论，构造评价指标集中的值Xn与大坝评价等级k之间的单指标联系度μnk，根据前文所述，本模型共有5个评价等级，且评价指标值Xn随评价等级的增大而增大，因此，采用式(3)至式(7)求得大坝运行风险评价模型各指标与各评价等级之间的联系度。

(3)

(4)

(5)

(6)

(7)

式中：s0至s5为评价指标值的临界值。

3.3.2熵值法计算指标权重

根据上述理论，计算各个指标的权重，主要计算步骤如下：

(1) 构建m个等级n个评价指标的判断矩阵B，即

(8)

(2) 将判断矩阵归一化处理，得到归一化判断矩阵R，即：

(9)

式中xmax和xmin分别为同一指标下不同等级中的最优值和最劣值。

(3) 确定第j个评价指标的熵，即

(10)

其中：

(11)

当Pij= 0 时，lnPij无意义，此时对其计算修正为

(12)

(4) 计算各评价指标的权重，即

(13)

3.3.3计算综合联系度

根据式(14)计算指标n与评价等级k之间的综合联系度vik，即

(14)

3.3.4确定评价等级

依据集对分析基本原理，最大综合联系度所对应的评价等级即为大坝运行风险评价等级[9]，即

(15)

4工程实例

4.1基本资料

某水电站是一座以发电为主，兼有防洪、灌溉等综合利用的大型水力枢纽工程，其工程等别为Ⅰ等，主要建筑物设计标准为1级，设计洪水位为111.00 m，水库的设计正常蓄水位为108.00 m，校核洪水位为114.00 m，总库容216.26亿m3。大坝为混凝土宽缝重力坝，坝顶高程115 m，最大坝高105 m，坝顶长446.50 m，大坝自右至左共分26个坝段，坝轴线呈折线，两岸折向上游。两岸为挡水坝段，中间为9孔溢流坝段，长73.0 m，最大泄量为13 200 m3/s[17-18]。

现对其运行安全风险状况进行评价。根据前文所构建的评价指标体系，聘请S1,S2, …,S5共5位专家对该坝的运行管理(B1)、工程质量(B2)、防洪安全(B3)、结构安全(B4)、渗流安全(B5)、金属结构安全(B6)、抗震安全(B7)7项指标做出评判，评分区间为[0,1](分数越高表示越安全)，具体分数如表2所示。

4.2指标联系度

根据上述原理，将专家打分值的平均值作为目

表2　专家评分表

前该指标的评判值，以表1所示区间划分为评判标准，按照式(3)至式(7)分别计算出各单指标联系度以及它们与各评价等级之间的联系度，如表3、表4所示。

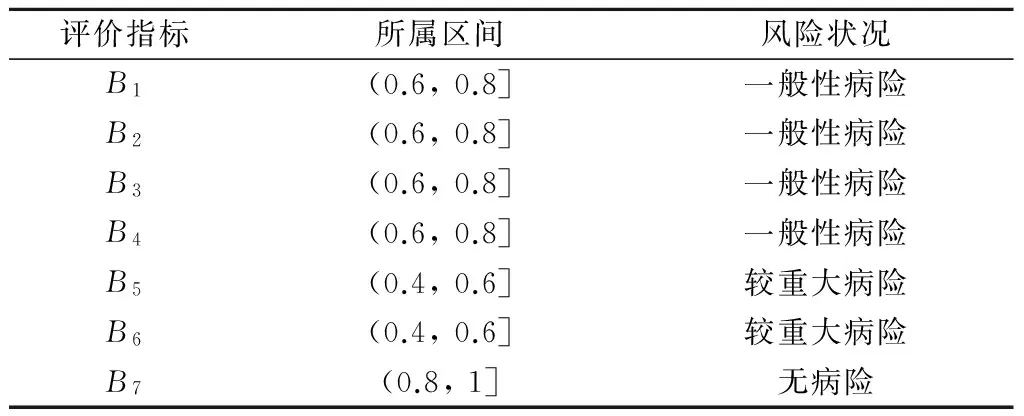
表3　单指标评价结果

表4　各指标与评价等级之间联系度

4.3熵值法计算各指标权重

首先根据专家评分表，得到判断矩阵为

根据式(9)计算得到归一化判断矩阵为

然后根据式(10)至式(13)计算得到各指标权重为

ω=(0.2630.0950.2630.0950.0950.0950.095)T。

4.4计算综合联系度

根据计算出的各指标与评价等级之间的联系度，按照式(14)进行加权处理，得到各指标综合联系度为

v=(-0.143-0.1080.0350.102-0.035)T。

4.5确定大坝运行风险评价等级

依据式(15)，最大联系度为0.102，其对应评价等级区间为(0.6,0.8]，进而得出该坝目前的运行风险状况为一般性病险，与实际情况相符。考察相邻评价等级区间所对应联系度的符号，可以进一步预估该坝有向较重大病险发展的趋势，同时，根据各指标权重分布，可以看出该坝主要存在运行管理和防洪安全2个方面的风险隐患，建议及时采取工程措施、加强运行管理，进一步降低大坝运行风险。

5结论

大坝运行安全风险评价是一项需要兼顾多指标、多层次属性的系统工程。本文利用集对分析方法对大坝运行安全风险评价中的各指标与各评价等级之间的联系度进行计算，并结合熵值法对评价指标赋权，从而对大坝运行安全风险进行综合评价。

(1) 根据大坝运行期风险评价的相关理论和原则确定了大坝运行期风险评价所需的各项指标，构建了大坝运行期风险评价指标体系，并确立了大坝运行风险等级标准。

(2) 确定权重是建立大坝运行安全风险评价模型的关键步骤，为了避免人为赋权的主观随意性，本文引入信息论中的熵理论对大坝运行风险评价指标进行客观赋权，提高了评价的精度。

(3) 利用集对分析法构建了大坝运行安全风险评价模型，该模型从同、异、反3个方面综合考虑影响大坝运行安全的众多确定和不确定性因素，是一种定性与定量相结合的评价方法。工程实例表明，将本文建立的大坝运行安全风险评价模型应用到实际工程中是可行且有效的。

参考文献：

[1]吴中如. 中国大坝的安全和管理[J]. 中国工程科学,2000,2(6):36-39.

[2]郑小武, 刘立. 基于集对分析的土石坝安全风险评价[J]. 人民黄河,2013,35(11):93-95，98.

[3]马福恒. 病险水库大坝风险分析与预警方法[D].南京：河海大学,2006.

[4]李晓璐,李春雷,李德玉,等. 基于多层次模糊分析法的大坝安全评价研究[J]. 人民长江,2010,41(17):92-95.

[5]杨灿, 郭曙光, 陈建康. 重力坝安全运行风险评价[J]. 吉林水利,2015,(3):5-9.

[6]SU Huai-zhi, QIN Peng, QIN Zhi-hai. A Method for Evaluating Sea Dike Safety[J]. Water Resource Manage, 2013, 27(10): 5157-5170.

[7]WEI Yong, XU Kai-Li. Application of Set Pair Analysis on Safety Evaluation of Tailing Dam Stability[J]. Journal of Safety Science & Technology, 2012，8(9):101-105.

[8]张国栋,李雷,彭雪辉. 基于大坝安全鉴定和专家经验的病险程度评价技术[J].中国安全科学学报,2008,(9):158-166.

[9]SL258—2000，水库大坝安全评价导则[S]. 北京:中国水利水电出版社，2000.

[10]赵克勤. 集对分析及其初步应用[M]. 杭州：浙江科学技术出版社, 2000.

[11]DECAI H, KEQIN Z, PING Z. Uncertainty Network Planning Technique Using the Connection Number a+bi of Set Pair Analysis[C]∥Proceedings of the 3rd World Congress on Intelligent Control and Automation. IEEE, Hefei, China. June 28-July 2, 2000:1997-2000.

[12]秦植海, 秦鹏. 高边坡稳定性评价的模糊层次与集对分析耦合模型[J]. 岩土工程学报,2010,32(5)：706-711.

[13]WANG T, CHEN J S, WANG T,etal. Entropy Weight-set Pair Analysis Based on Tracer Techniques for Dam Leakage Investigation[J]. Natural Hazards, 2014, 76(2):1-21.

[14]邱宛华. 管理决策与应用熵学[M].北京:机械工业出版社,2002:193-196.

[15]TZENG S R, KALODIMOS C G. Protein Activity Regulation by Conformational Entropy[J]. Nature, 2012, (488): 236-240.

[16]TAO J, FU M, SUN J,etal. Multifunctional Assessment and Zoning of Crop Production System Based on Set Pair Analysis: A Comparative Study of 31 Provincial Regions in Mainland China[J]. Communications in Nonlinear Science & Numerical Simulation,2014, 19(5):1400-1416.

[17]苏怀智, 孙小冉. 混凝土坝渗流性态综合评价与趋势预估模型研究[J]. 人民长江,2013,(22): 95-99, 110.

[18]秦鹏，张喆瑜，秦植海,等. 滑坡体监测数据的改进变维分形——人工神经网络耦合预测模型[J].长江科学院院报，2012,29(3)：29-33.

(编辑：陈敏)

WU Sheng-wen1, QIN Peng1, 2, GAO Jian1,YAN Xiao-qun2

(1. Institute of Hydraulic and Environmental Engineering, Zhejiang University of Water Resource and Electric

Power, Hangzhou 310018, China; 2. College of Water Conservancy and Hydropower Engineering,

Hohai University, Nanjing210098, China)

Application of Entropy Weight and Set Pair Analysis Theory toRisk Assessment of Dam Operation

Abstract:Establishing proper evaluation indexes and criterion and making accurate judgment on dam’s operational risk according to the real operation condition is important for operation management in water conservancy projects. However, complex fuzzy, nonlinear relations exist between the evaluation indexes and criterion. Set pair analysis method has priority in quantitatively dealing with uncertainty problems between multi-factors, hence it can be used for the evaluation of dam’s operational risk. An assessment model for dam’s operational risk based on entropy theory and set pair analysis theory was built. The index weights were determined through calculation of information provided by each factor. The model was applied to evaluate the operation risk of a dam, and the safety level of the dam was obtained and the development trend of the risk was predicted. Results showed that the present method based on set pair analysis and entropy theory is simple and feasible, scientific and reasonable, and offers new idea for the assessment of dam’s operation risk.

Key words:dam; operation safety; risk assessment; information entropy; set pair analysis

收稿日期：2015-12-22；修回日期：2016-01-06�

基金项目：水利部公益性行业科研项目(201401010)；浙江省自然科学基金项目(LQ15E090003)；浙江省水利厅项目(RC1534,RC1548)；浙江水利水电学院高等教育教学改革项目(JG201508)

作者简介：吴胜文(1968-)，男，安徽安庆人，讲师，主要从事水安全监控理论的教学与科研工作，(电话)0571-86929059(电子信箱)wusw1221@163.com。

doi:10.11988/ckyyb.20151101

中图分类号：TV698.2

文献标志码：A

文章编号：1001-5485(2016)06-0036-05

2016,33(06):36-40