基于整体分析法的抗滑桩加固边坡稳定性分析

张　谭，郑　宏，聂治豹

(北京工业大学 建筑工程学院，北京　100124)

基于整体分析法的抗滑桩加固边坡稳定性分析

张谭，郑宏，聂治豹

(北京工业大学 建筑工程学院，北京100124)

摘要：为了分析抗滑桩加固边坡的稳定性，将整体分析法应用于抗滑桩加固边坡的稳定性计算中，重新推导了加固边坡安全系数的计算公式。该方法以整个滑坡体代替传统的条块为分析对象，通过建立三力矩平衡方程而非传统的水平力平衡、竖直力平衡以及对一点的力矩平衡，实现了滑体的整体极限平衡稳定性分析。所得到的方程是刻度良好的，存在唯一的、安全系数为正的实数解，收敛范围大且迅速，具有良好的数值特性，并且适用于各种形式的滑动破裂面，可以方便地从二维向三维进行推广。最后通过算例验证了所提方法的有效性。

关键词：边坡稳定性；抗滑桩；极限平衡；整体分析；数值特性

1研究背景

有限元方法是抗滑桩-边坡稳定分析的一种综合性方法，可以同时给出桩的位移及边坡的安全系数。然而，有限元方法通常需要较高的数值成本,且桩土界面的非线性使得收敛变得困难。而极限平衡法应用简便，是目前边坡稳定性分析最常用的方法。在实际应用中，对抗滑桩加固边坡稳定性的研究通常采用对传统的边坡计算方法进行扩展，将抗滑桩提供的加固力包含进去的方式。

1981年Ito等[1]利用极限平衡法处理抗滑桩加固边坡问题，该方法中被加固边坡的安全系数定义为作用在滑体上抗滑力矩与倾覆力矩的比值，抗滑桩提供的抗滑力矩采用1975年Ito等[2]推导的土体移动引起的单排桩的水平力理论方程计算。然而，这一安全系数不同于被广为采用的基于强度储备概念的安全系数[3]。

Lee等[4]采用简化毕肖普法搜索最危险滑动面并计算滑体的倾覆力矩与抗滑力矩，运用边界元的方法计算土体移动抗滑桩所承受的水平力。Hassiotis等[5]在边坡稳定分析中采用扩展摩擦圆方法来考虑抗滑桩的作用，并使用Ito与Matsui方程计算滑体作用在单排抗滑桩上的水平力。Ausilio等[6]使用极限分析的动态方法来计算抗滑桩加固边坡的稳定性，将安全系数定义为土壤强度参数的折减系数，在滑动面处增加一个水平力和一个力矩来考虑抗滑桩的加固作用。Nian等[7]和Li[8]同样采用极限分析动态方法，前者考虑非均质、各向异性土体并假定抗滑桩提供的抗滑力与滑动面相切，后者采用Ito与Matsui方程计算滑体移动作用在单排抗滑桩上的水平力。Zeng等[9-11]基于不平衡推力传递系数法，将设桩处土条的滑坡推力乘以一个<1的折减系数来考虑桩间的土拱效应。

张友良等[12]、邹广电等[13]以传递系数法为基础，前者将极限平衡法和有限单元法相结合，抗滑桩作为一特殊的分条进行处理，抗滑桩对桩前土体的作用力用有限单元法计算并作为条外分力传递给下一分条；后者提出抗滑桩的整体设计方法，在设桩处的分条上增加一项抗滑力并使用日本土木研究所公式计算单桩极限状态的抗滑力。

在以上分析加固边坡稳定性的方法中，条块或滑体的平衡方程一般采用平面力系的基本形式，即水平力平衡、竖直力平衡以及对一点的力矩平衡，然而基本形式中力平衡方程与力矩平衡方程的量纲不一致，力平衡方程中未知数的系数通常也远小于力矩平衡方程中未知数的系数。因此，由基本形式所得到的方程组是不良刻度的，一般需进行合理的刻度化处理，才能直接进行整体求解。并且传统的极限平衡法收敛性存在一定的问题，众所周知，即使对于非常简单的问题，通过严格条分法得到的方程使用牛顿法求解时收敛范围都很小。

本文以整体分析法为基础，整体分析法采用平衡条件的三力矩形式而不是基本形式来建立滑体的平衡方程组，所得到的方程组刻度良好(刻度良好表示所有方程未知数的系数数量级及单位一致)，无需再进行刻度化，可以直接利用牛顿法求解，并且具有良好的数值特性，收敛范围大且迅速，计算精度高，适用于各种形式的滑动面。

2边坡稳定性的整体分析法简介

郑宏等[14]提出了一种边坡稳定分析的无条分法，后来又被称为整体分析法[15]。该方法以整个滑体为分析对象，无需对滑体进行条分。

如图1所示，假定滑体Ω由边坡外轮廓线g与某一潜在滑动面S所围成的平面区域组成，滑体可以包含各种不同介质。

图1　滑体受力Fig.1　Sketch of forces on a sliding body

(1)

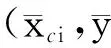
(2)

(3)

(4)

(5)

(6)

假设滑面满足摩尔-库伦准则，当滑体处于极限平衡状态时有

(7)

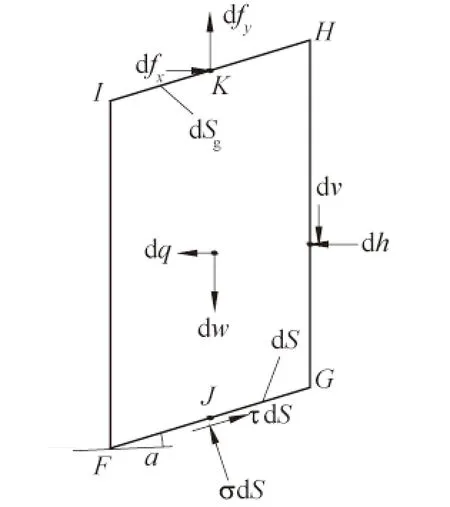
图2　微分条块的受力Fig.2　Sketch of forceson a differential slice

其中：FS为安全系数；ce和fe为有效应力抗剪强度参数；u为孔隙水压力。

为了假定滑动面正应力的分布，沿滑动面S的阻滑方向取一弧长为dS的微分条块FGHI，如图2所示。其中，dw和dq为条块自重和水平地震力；dν和dh为垂直和水平条间力增量；dfx和dfy为作用在边坡外轮廓线上的荷载在条块上的水平和垂直力分量，即

(8)

将微分条块上各力向滑动面的法线方向投影得

σdS=dwcosα-dqsinα+dfxsinα-

(9)

(10)

式中σ0和σI分别为滑体上的外荷载和条间力所引起的滑面正应力。

根据式(10)的提示来构造滑面正应力分布形式的逼近式,即

(11)

其中f(x，a,b)为滑动面应力修正函数；a和b为待定参数；σ0可分解为

(12)

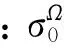
其中：

(13)

(14)

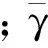
(15)

文献[17]中将f(x，a,b)取为线性函数，即

(16)

其中：

(17)

将式(7)、式(11)、式(16)代入式(1)并整理得

g(FS,a,b)=FS(au1+bu2+u3)+

au4+bu5+u6=0 。

(18)

式中：g是关于FS，a，b的3阶非线性向量函数，u1至u6是6个三阶向量，即：

(19)

(20)

(21)

(22)

(23)

(24)

式(18)为关于FS,a和b的三元二次方程组(可以展开为6个方程)，利用式(18)的前2式可以解出以FS表示的a和b，再代入到第3式中即可得到一个关于FS的一元三次方程，因为一元三次方程至少有一个实根，所以可得到边坡的安全系数FS。

3整体分析法计算抗滑桩加固边坡安全系数

前面介绍的整体分析法没有考虑抗滑桩加固的情形，对于抗滑桩支护体系，抗滑桩穿过假定的滑动面时，需考虑抗滑桩在滑动面处切向的抗滑作用。现将滑动面S分成S1和S22部分，如图3所示。假定设桩后滑面正应力的分布仍满足式(11)，设桩处滑面(即S2部分)剪应力由抗滑桩在滑面处提供的抗滑力Q计算，滑面其他部分(即S1部分)剪应力仍服从摩尔-库伦准则。

图3　抗滑桩加固滑体示意图Fig.3　Sliding body reinforced by anti-sliding pile

(25)

其中：

(26)

式中：A为抗滑桩正截面面积；αK为抗滑桩中心在滑面处的切向角。

未进行抗滑桩设计时，Q可根据简化毕肖普法进行估算。设边坡处于临界状态，抗滑桩加固后边坡的最危险滑动面位置不变，当安全系数达到理想的FS时，桩在滑面处应对滑体提供的抗滑力为

(27)

(28)

其中：Wi表示土条自重；αi为第i条块底面的切向角；li为第i条块的底面长度；ci，φi及ui分别表示条块底面的有效黏聚力、有效内摩擦角及孔隙水压力。

抗滑桩设计完成之后，Q可由桩的斜截面抗剪力计算[16]，即

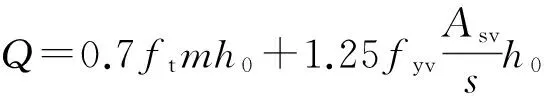
(29)

式中：ft为混凝土抗拉强度设计值；m为截面宽度；h0为截面有效高度；fyv为箍筋的抗拉强度设计值；Asv为同一截面箍筋的截面积；s为箍筋间距。

因为文中滑体的计算宽度均为单位宽度，由上式求得的剪力Q应除以抗滑桩的桩轴间距，且计算得到的抗剪力应大于由式(29)计算得到的为达到理想安全系数抗滑桩在滑面处提供的抗滑力。

然后将式(11)、式(16)及式(26)代入式(25)并整理得

au4+bu5+u6=0 。

(30)

与之前一样，g是关于FS,a,b的3阶非线性向量函数，u1至u7为7个三阶向量，定义为:

(31)

(32)

(33)

(34)

(35)

(36)

(37)

如果滑动面是由解析式可知的曲线段组成，式(31)至式(37)中的各项可以被精确计算出来。然而考虑到滑面形式的多样性，而且条分法的经验表明当条块数充分大时，条块数对安全系数的影响很小，所以本文也采用了类似的简化处理：将滑动面分成若干个小区间，每个小区间内的法向应力等于其区间中心点的法向应力，然后再对式(31)至式(37)进行中心积分。

需要注意的是在计算式(33)时，抗滑桩加固段的坡体(即S2段)其单位重度γ相较于加固之前土的重度会增大，应根据土和桩所占的比例求加权平均重度。

最后通过求解式(30)，即可得到考虑抗滑桩加固作用边坡的安全系数。

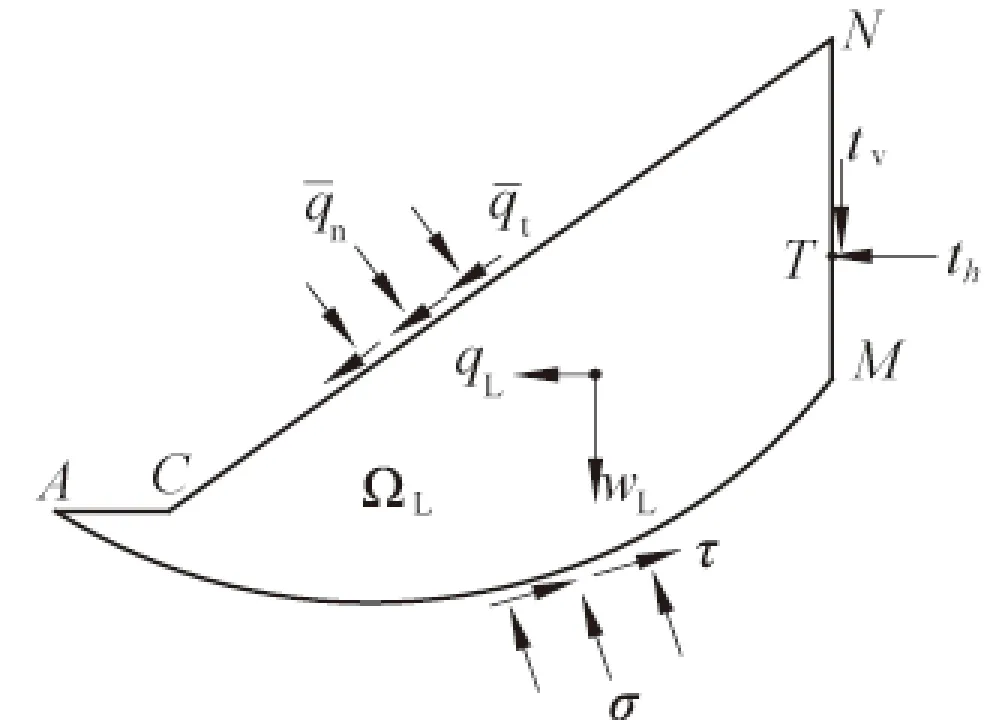
图4　下滑体受力Fig.4　Forces on thelower part of a sliding body

滑体内推力大小及推力线可根据文献[17]中的方法计算：在x=x0处将滑体切成上、下2部分，取下一部分为研究对象，受力如图4所示。

根据水平及竖向力的平衡可以分别得到水平推力和竖向推力为

(38)

再以原点为力矩中心，可以得到推力的作用点y的坐标,即

(39)

其中mL为wL和qL对坐标原点的力矩。

4算例

4.1算例1

均质边坡的坡高为20m，坡度为1∶2。滑动面为以(35.1m,55m)为圆心的圆弧，强度参数及几何参数如图5所示。

图5　例1边坡几何及强度参数Fig.5　Geometrical and mechanical parameters ofslope in example 1

边坡加固前，使用整体分析法计算得到的安全系数为1.058，现拟在x=40m处对边坡进行加固，假设治理后安全系数FS=1.35，抗滑桩在滑面处应提供的抗滑力根据式(27)估算，取Q=600kN。使用边长为1m的方桩，抗滑桩单排设置，桩心间距为3m。使用文献[12]中的方法得到加固后的安全系数为1.354。

使用本文提出的方法，得到加固后边坡的安全系数为1.348， 同时可以得到水平推力及边坡推力线如图6所示。

(a)水平推力(b)边坡推力线图6 例1水平推力和边坡推力线Fig.6 Horizontalpushingforceandthrustlineofexample1

4.2算例2

分层边坡[17]非圆弧滑动面，强度及几何参数如图7和表1所示。

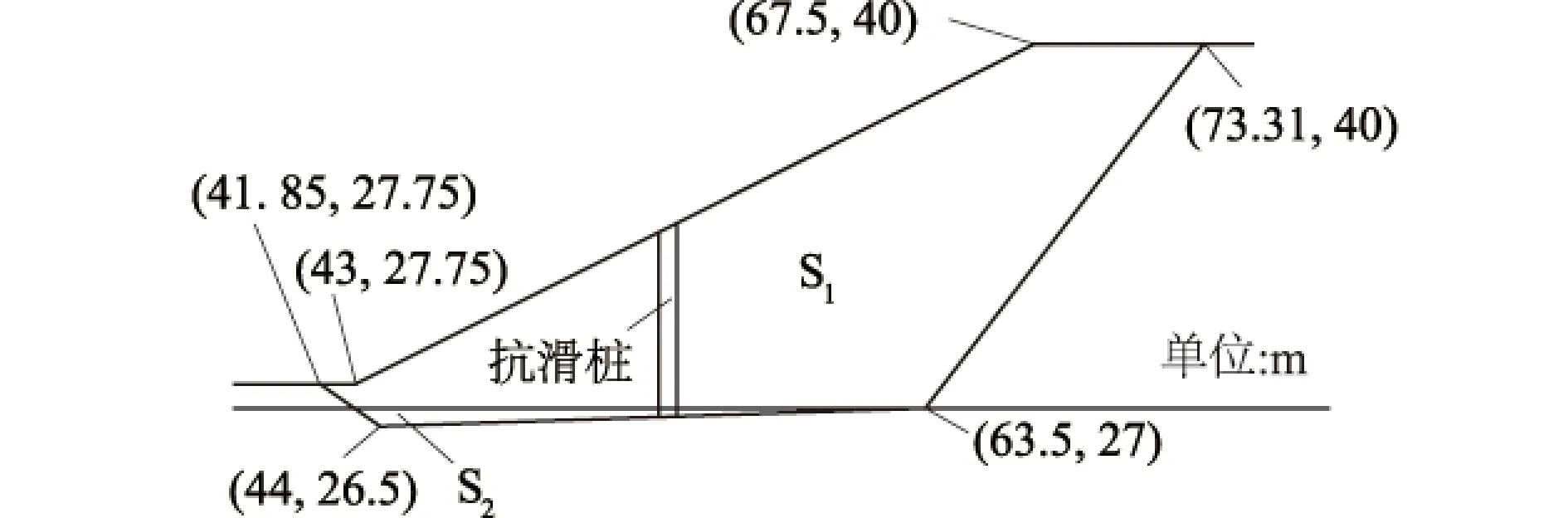
图7　例2边坡几何及强度参数Fig.7　Geometrical and mechanical parametersof slope in example 2

滑面ce/kPaφe/(°)γ/(kN·m-3)S128.52018.84S20.01018.84

边坡加固前，使用整体分析法计算得到的安全系数为1.287，现拟在x=54m处对边坡进行加固，假设治理后安全系数FS=1.5，抗滑桩在滑面处应提供的抗滑力根据式(27)估算，取Q=200kN。使用边长为1m的方桩，抗滑桩单排设置，桩心间距为4m。使用文献[15]中的方法得到加固后边坡的安全系数为1.673。

使用本文提出的方法，得到加固后边坡的安全系数为1.628，水平推力及推力线如图8所示。

图8 例2水平推力和边坡推力线Fig.8 Horizontalpushingforceandthrustlineofexample2

可以看到，推力线在临近滑面顶端的时候跑出滑体，为了解决这一问题，在x=72m处增设一竖向的拉力缝。然后使用文献[12]中的方法计算得到新的安全系数为1.597，使用本文的方法新得到的安全系数为1.554，明显低于之前的1.628，新得到的水平推力及推力线如图9所示。

图9 增设拉力缝后水平推力大小和边坡推力线Fig.9 Horizontalpushingforceandthrustlineaftersettingatensioncrack

5结语

将整体分析法应用于抗滑桩加固边坡稳定分析计算中，重新推导整理出了包含安全系数的方程表达式，该方法相对于其他极限平衡条分法具有明显的优势，可以提高计算的精度、简化程序的数据结构，并具有优异的数值特性。最后通过算例表明该方法是正确的、可靠的。

参考文献：[1]ITO T, MATSUI T. Design Method for the Stabilizing Piles against Landslide—One Row of Piles[J]. Soils and Foundation, 1981, 21(1): 21-37.

[2]ITOT,MATSUIT.MethodstoEstimateLateralForceActingonStabilizingPiles[J].SoilsandFoundation, 1975, 15(4) : 43-59.

[3]ZHENGH,THAMLG,LIUDF.OnTwoDefinitionsoftheFactorofSafetyCommonlyUsedinFiniteElementSlopeStabilityAnalysis[J].ComputersandGeotechnics, 2006, 33(3): 188-195.

[4]LEECY,HULLTS,POULOSHG.SimplifiedPile-slopeStabilityAnalysis[J].ComputersandGeotechnics, 1995, 17(1): 1-16.

[5]HASSIOTISS,CHAMEAUJL,GUNARATNEM.DesignMethodforStabilizationofSlopeswithPiles[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 1997, 123(4): 314-323.

[6]AUSILIOE,CONTEE,DENTEG.StabilityAnalysisofSlopeswithPiles[J].ComputersandGeotechnics, 2001, 28:591-611.

[7]NIANTK,CHENGQ,LUANMT.LimitAnalysisoftheStabilityofSlopesReinforcedwithPilesagainstLandslideinNonhomogeneousandAnisotropicSoils[J].CanadianGeotechnicalJournal,2008,45(8): 1092-1103.

[8]LIX,HES,WANGC.StabilityAnalysisofSlopesReinforcedwithPilesUsingLimitAnalysisMethod[C]∥AdvancesinEarthStructures:Geo-ShanghaiInternationalConference2006.ASCE.Shanghai,China,June6-8, 2006: 105-112.

[9]ZENGSan-ping,LIANGRY.StabilityAnalysisofDrilledShaftsReinforcedSlope[J].SoilsandFoundations, 2002, 42(2): 93-102.

[10]YAMINM,LIANGRY.LimitingEquilibriumMethodforSlope/drilledShaftSystem[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2010, 34(10): 1063-1075.

[11]LIANGRY,JOORABCHIAE,LINL.AnalysisandDesignMethodforSlopeStabilizationUsingaRowofDrilledShafts[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2014, 140(5):1-12.

[12]张友良, 冯夏庭, 范建海，等.抗滑桩与滑坡体相互作用的研究[J]. 岩石力学与工程学报，2002，21(6):839-842.

[13]邹广电, 陈永平. 抗滑桩的极限阻力及其整体设计[J].水利学报, 2003，(6):22-29.

[14]ZHENGH,THAMLG.ImprovedBell’sMethodfortheStabilityAnalysisofSlopes[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2009, 33(14): 1673-1689.

[15]ZHENGH,ZHOUCB.GlobalAnalysisonSlopeStabilityanditsEngineeringApplication[J].ScienceinChinaSeriesE, 2009, 52(2): 507-512.

[16]熊峰，李章政，贾正甫，等. 结构设计原理[M].北京：科学出版社，2002: 123-134.

[17]陈祖煜. 土质边坡稳定分析[M].北京：中国水利水电出版社，2003: 117-119.

(编辑：陈敏)

Stability Analysis of Slope Reinforced with Pilesby Global Analysis Method

ZHANGTan,ZHENGHong,NIEZhi-bao

(CollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China)

Abstract:To analyze the stability of reinforced slopes, on the basis of the global analysis of slope stability, a new procedure is proposed to compute the factor of safety of slopes reinforced with piles. By taking the whole sliding body, instead of individual slices, as the analysis object, three equilibrium equations are formulated according to the moment equilibrium conditions. But in traditional method, we establish two force equilibrium equations(horizontal direction and vertical direction) and one moment equilibrium equation at a given point. By using the new method, we can obtain unique real number solution of the equation and positive safety factor. This method is not only suitable for slopes with slide surfaces of different shapes, but also possesses excellent numerical properties with a very large scope of convergence and a very rapid convergent rate.Moreover, it can be easily extended from two-dimension to three-dimension. Finaly, two examples are given to prove the effectiveness of this method.

Key words:slope stability; anti-sliding pile; limit equilibrium; global analysis; numerical feature

收稿日期：2015-09-04；修回日期：2015-10-29

基金项目：国家自然科学基金项目(11172313);国家重点基础研究计划项目(2011CB013505,2014CB047100)

作者简介：张谭(1991-),男，山东金乡人，硕士研究生，主要从事数值计算及边坡加固研究，(电话)13161125076(电子信箱)495849591@qq.com。

doi:10.11988/ckyyb.20150746

中图分类号：TU473.1

文献标志码：A

文章编号：1001-5485(2016)06-0109-06

2016,33(06):109-114