三峡库区某滑坡土非饱和松弛特性试验研究及模型建立
2016-06-24刘佳龙王世梅胡秋芬
刘佳龙,王世梅,胡秋芬,郭 振
(1. 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌 443002;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
三峡库区某滑坡土非饱和松弛特性试验研究及模型建立
刘佳龙1,2,王世梅1,2,胡秋芬1,2,郭振2
(1. 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌443002;2.三峡大学 土木与建筑学院,湖北 宜昌443002)
摘要:为了解基质吸力对非饱和土松驰特性的影响,利用GDS非饱和三轴仪的高级加载模块对三峡库区某滑坡土样开展了不同基质吸力的非饱和松弛试验,选取了与试验松弛曲线较一致的指数函数、对数函数、幂函数分别进行了曲线拟合,在对3种拟合结果进行对比分析基础上,确定了拟合精度最高的幂函数作为松弛模型,并分别求出了不同基质吸力作用下松弛曲线的模型参数。同时分析了各模型参数与基质吸力之间的相关性,并建立了模型参数与基质吸力之间的关系函数,据此建立了能反映基质吸力影响的非饱和土松弛模型。
关键词:滑坡;非饱和土;基质吸力;松弛模型;松驰特性
1研究背景
大量实例表明,水库滑坡的变形及失稳与水的作用密切相关[1]。一方面,在降雨入渗及库水位变动作用下,滑坡土体在饱和状态与非饱和状态之间转化,具有非饱和特性;另一方面,滑坡土体在水作用下的变形大都经历了一个时间过程,又具有流变特性,对滑坡的长期变形进行数值模拟时若再考虑渗流效应情况下耦合土体流变效应,其结果将更加符合滑坡变形的真实状态。因此,非饱和土流变特性的研究对水库滑坡的变形和失稳预测具有十分重要的意义。土体流变特性应力松弛和蠕变虽然被同一物理机制所控制,但两者在宏观上却又有很大不同,应力松弛只是由于土体内部结构的弱化而引起的内部应力降低,应力松弛规律是研究应力随时间的变化关系。
目前关于土体松弛特性研究较多。李翠华等[2]对饱和软黏土进行了多组直剪松弛和三轴松弛试验,得到了饱和黏土的松弛特性,并建立了描述松弛特性的经验数学方程。尹清杰等[3]借助于GDS三轴仪的高级加载模块,进行了饱和土的松弛特性试验,建立了饱和土的松弛模型。肖宏彬等[4]对广西南宁非饱和膨胀土进行了一系列室内试验研究,探讨了非饱和膨胀土非线性流变特性。王琛等[5]针对以一个试样进行分级加载松弛试验的可行性问题,并研究堆石料的应力松弛规律,使用大型三轴仪对堆石料进行常应变速率排水压缩试验和不同围压、不同应变水平的分级加载排水松弛试验,并建立了双曲线应力松弛方程。上述对土松弛特性的研究,基本上是针对饱和土,真正能反映非饱和土体松弛特性的试验研究却很少。为了解基质吸力对非饱和土松弛特性的影响,本文开展了非饱和土松弛特性的研究,利用GDS的高级加载模块进行了5种不同基质吸力作用下的松弛试验,并对试验获取的松弛曲线进行了拟合和分析。
2松弛试验
2.1试验土样
试验土样取自三峡库区某滑坡滑带顺层部分的黄色软塑状土,基本物理力学性质见表1。

表1 土的基本物理参数
2.2试验仪器
松弛试验是在保持应变不变的条件下测试应力随时间降低的过程,通过松弛试验可以建立土的松弛模型,并进一步预测土的长期强度,从而为预测滑坡的长期稳定性提供计算参数。非饱和松弛试验不仅要在土样产生一定的应变值,并保持该应变值不变的条件下测试应力随时间降低的过程,而且还要在试验过程中能够控制基质吸力。目前这样的松弛试验仪器在国内外都没有见到,为了开展非饱和松弛试验,笔者借助GDS非饱和三轴仪(见图1)的高级加载模块(见图2),实现了非饱和松弛试验的加载、应变控制和基质吸力控制等要求。
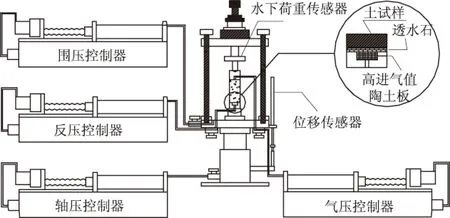
图1 GDS三轴试验系统
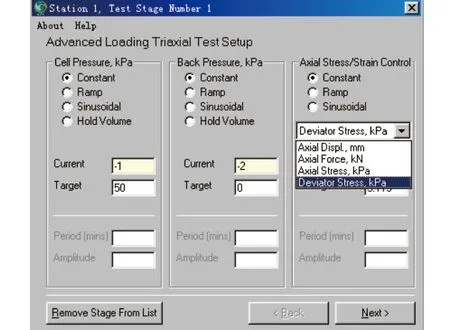
图2 GDS三轴仪高级加载模块应力及应变控制选项Fig.2 Stress and strain control options of advancedload module of GDS triaxial apparatus
2.3试验方法
与常规土松弛试验相比,非饱和土三轴松弛试验在固结及剪切松弛的整个过程中对试样都要施加预定的基质吸力。试验前准备工作见文献[6]。试验步骤为:
(1) 使用国产四联式非饱和土直剪仪测定非饱和土抗剪强度参数[6-7],此试验不再赘述,并计算相应的剪切强度峰值τf。
(2) 对试样施加围压和孔隙气压力进行排水固结,直至土样固结稳定。
(3) 当土样固结基本完成后,选择GDS的高级加载模块,按一定的剪切速率(通常取0.15mm/min),对试样进行剪切,剪应力q随着剪应变的增加而加大,当q达到峰值强度的80%~90%时,停止剪切。
(4) 进行应力松弛,在GDSLAB中选择AdvancedLoading实验模块,并在AdvancedLoadingTriaxialTestSetup中选择“围压保持不变、反压不变、应变保持不变”的加载方案。GDS仪器会自动保持当前剪应变不变,记录在此过程中的偏应力-时间关系曲线等。
2.4试验方案
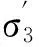

表2 非饱和土松弛试验方案
2.5试验结果
应力松弛过程中数据采集时间间隔为60s,GDS的数据处理模块自动将试验数据绘制了5条松弛曲线,见图3。
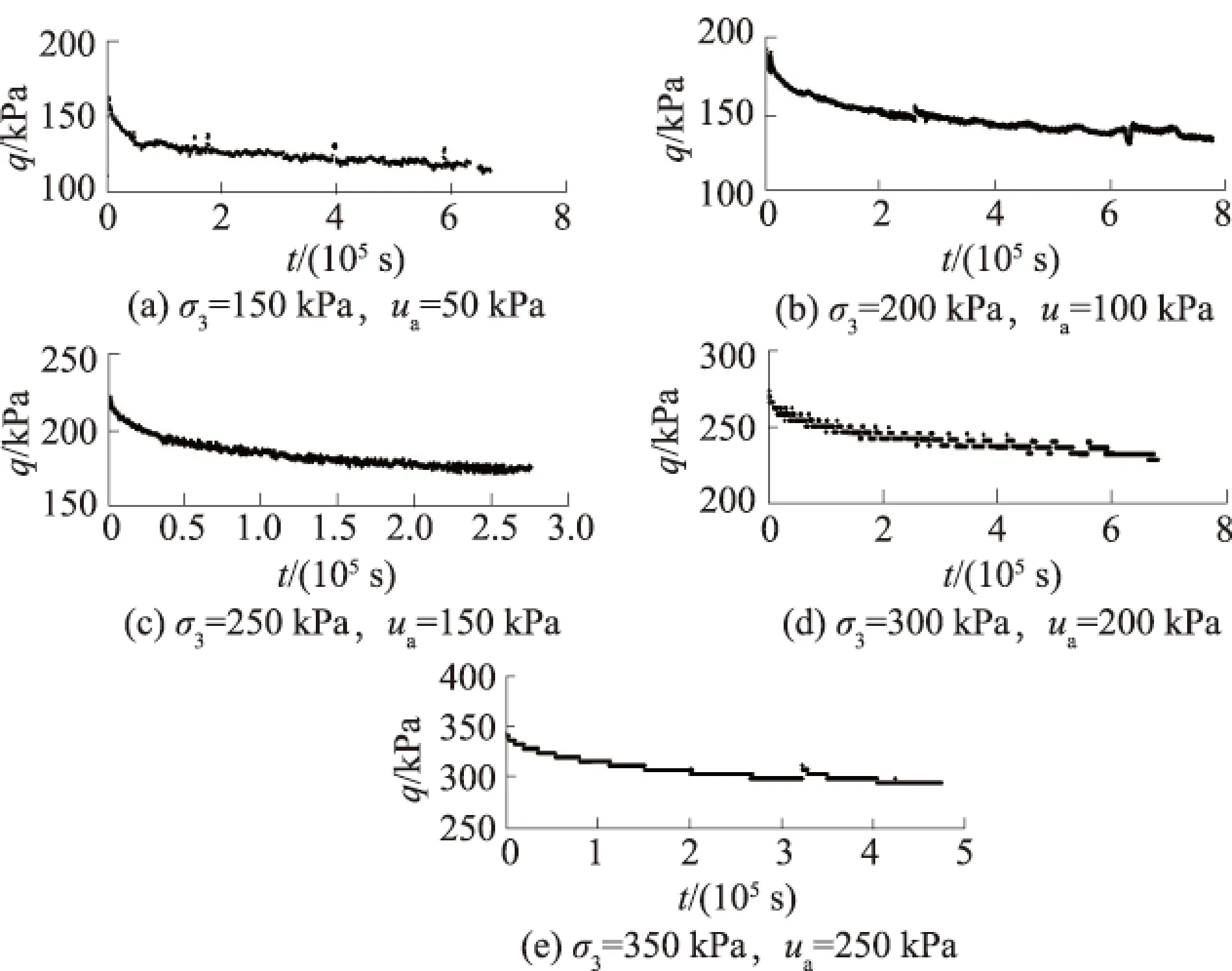
图3 不同基质吸力条件下非饱和应力松弛曲线Fig.3 Stress relaxation curves of unsaturated soil underdifferent matric suctions
由图3可见,不同基质吸力下的应力松弛曲线形态都非常类似,松弛过程大致可分为2个阶段:松弛应力快速下降阶段和松弛应力缓速下降阶段。松弛应力快速下降阶段特征非常明显,初始时土的应力松弛曲线下降较快,应力松弛的前几分钟松弛速度为1~10kPa/(60s),大约600s之后随时间的持续偏应力逐渐趋向于某一稳定值。之后,松弛应力下降速度降低为0.1~0.9kPa/(60s),并逐渐过渡到松弛应力缓速变化阶段,在松弛应力缓速下降阶段,应力松弛下降很小。
3非饱和土松弛模型
3.1拟合函数选取
由松弛曲线特征可知,指数函数、对数函数、幂函数等都可以用来模拟松弛曲线[2,6],以σ3=300kPa,ua=200kPa非饱和松弛曲线为例,分别采用指数函数、对数函数、幂函数来拟合曲线,如图4所示。
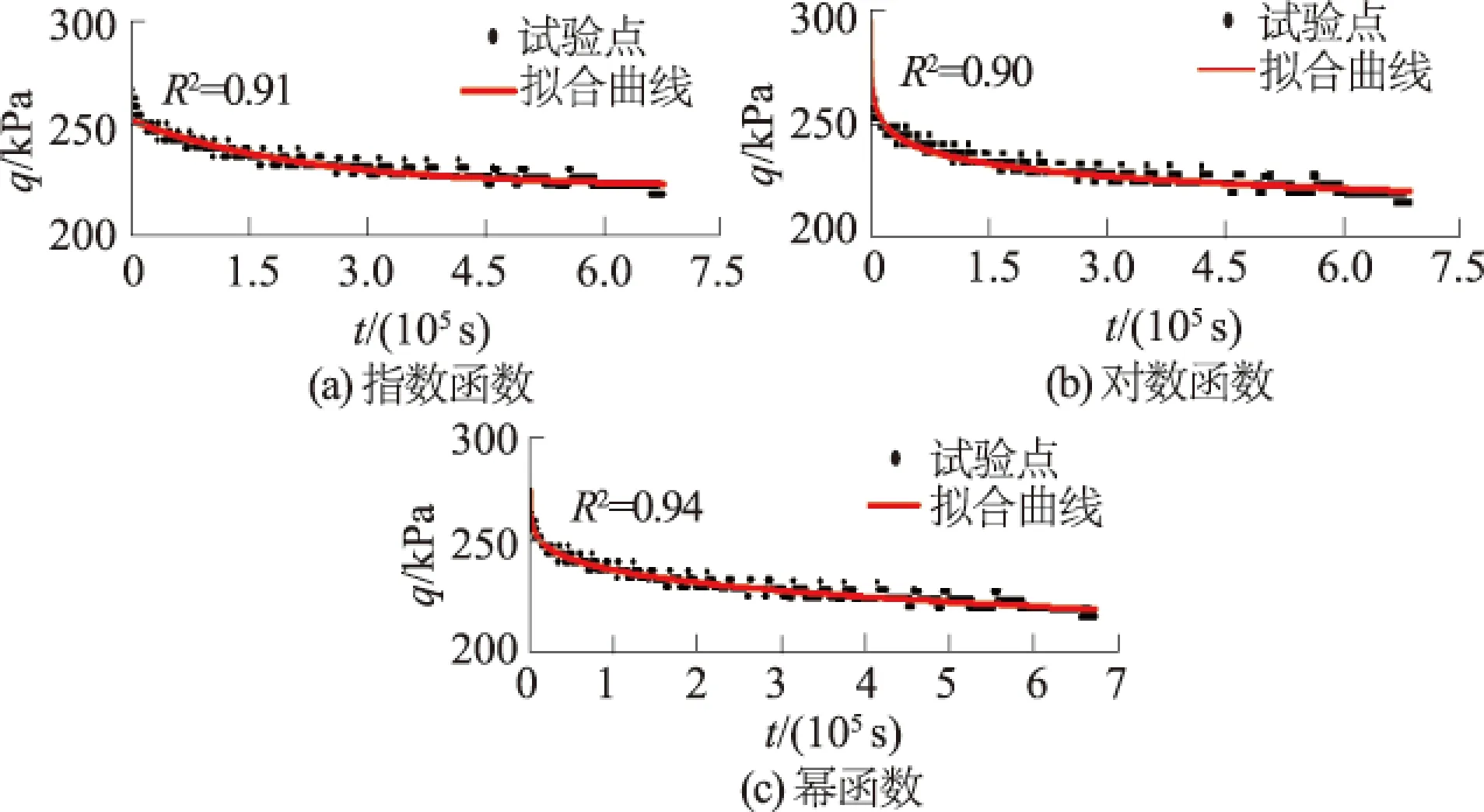
图4 σ3=300 kPa,ua=200 kPa时不同函数松弛曲线拟合对比Fig.4 Comparison of relaxation curve fitted by different functions when σ3=300 kPa, ua=200 kPa
由图4可知,指数函数拟合时在开始阶段与试验数据相差较大,拟合后决定系数为0.91,采用对数函数拟合时,刚开始松弛的偏应力值明显大于试验值,决定系数为0.90,而采用幂函数拟合后,可以发现拟合值与试验值能较好的吻合,决定系数也高于指数函数和对数函数拟合的结果。通过综合对比分析比较,采用如下幂函数作为此次滑坡土样的松弛模型[2],即
(1)
式中:s0,s,β为拟合参数;q(t)为偏应力;t为时间。
3.2各松弛曲线的模型参数
利用1stOpt(FirstOptimization)软件包对不同基质吸力下的松弛曲线进行模型参数求解。采用默认的全局优化算法,求得的模型参数见表3。
以σ3=150kPa,ua=50kPa为例,将表3中所列的参数代入松弛模型式(1)中,将得到的松弛曲线与试验得到的松弛曲线进行对比,如图5所示。由图可知,拟合曲线和试验数据能够较好的吻合。
3.3模型参数与基质吸力的相关性分析
通过分析表3中参数可知,模型参数s0,s,β与
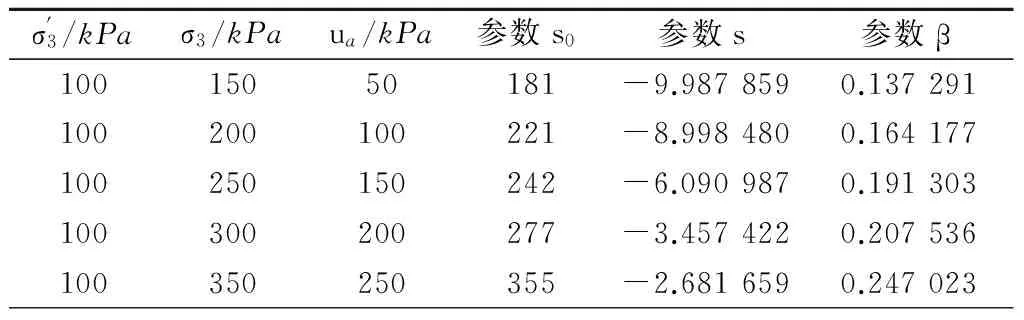
表3 不同基质吸力下的松弛曲线模型参数
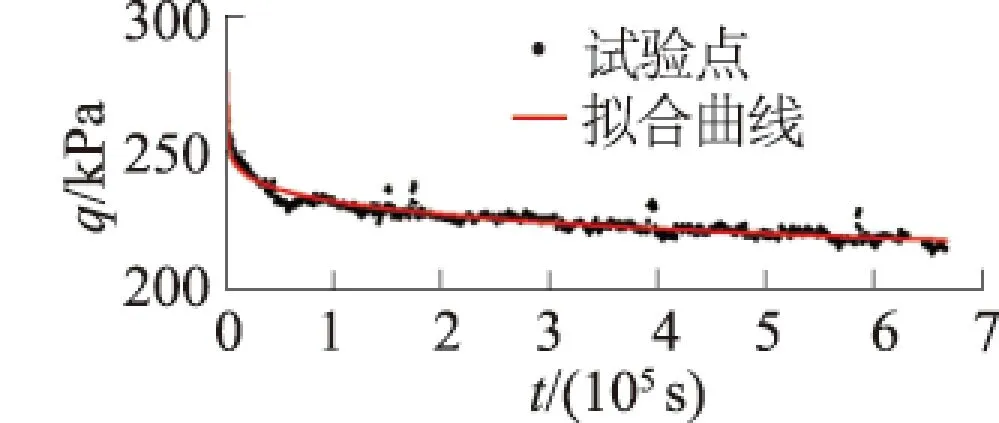
图5 σ3=150 kPa,ua=50 kPa时非饱和松弛曲线Fig.5 Relaxation curves of unsaturated soil (σ3=150 kPa,ua=50 kPa)
基质吸力之间存在线性关系,分别见图6。
由图6(a)可知,s0随ua的增大而增大。又由式(1)可知,当t=0时,q(t)=s0,即s0为开始松弛时刻的偏应力值。说明在相同的净围压下,随着基质吸力的增加,开始松弛时的偏应力初始值也增加。
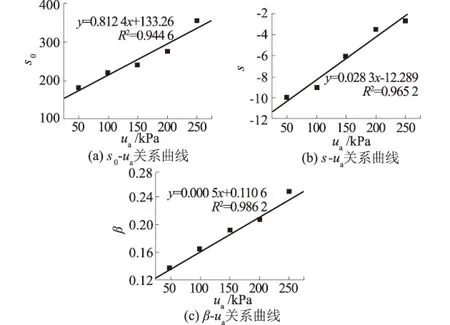
图6 模型参数与ua的关系曲线Fig.6 Relationship between model parameters and ua
由图6(b)可知,随ua的增大s的绝对值减小。又由式(1)可知,s主要影响曲线的“扁度”,即从开始松弛到最后趋于稳定时偏应力下降的相对范围。说明在相同的净围压下,随着基质吸力的增加,从开始松弛到最后趋于稳定时偏应力总在减小。
由图6(c)可知,β随ua的增大而增大。又由式(1)可知,β主要影响幂函数应力松弛时的偏应力变化率。说明在相同的净围压下,随着基质吸力的增加,松弛时的偏应力降低的速率也增加。
由上述分析可知,s0,s,β可分别表示为基质吸力的函数,即s0=0.812 4ua+133.26,s=0.028 3ua-12.289,β=0.000 5ua+0.110 6,代入式(1)中得非饱和土松弛模型为
q(t)=0.812 4ua+133.26+
(0.028 3ua-12.289)t0.000 5ua+0.110 6。
(2)
4结论与讨论
4.1结论
(1) 利用GDS非饱和三轴仪的高级加载模块实现了非饱和土的松弛试验。
(2) 通过指数函数、对数函数、幂函数对松弛曲线的拟合与对比分析,确定采用幂函数作为某滑坡土样的松弛模型。
(3) 采用1stOpt(FirstOptimization)软件包求取了不同机制吸力作用下松弛曲线的模型参数,建立了能反映基质吸力影响的某滑坡土样非饱和土的松弛模型。
4.2讨论
(1) 因温度及试验环境对试验数据会有一定的影响,导致试验数据有一定波动和个别数据出现偏离,在一定程度上影响了成果的精度。因此,试验研究中应严格控制试验温度及环境不受干扰。
(2) 本文选取的幂函数形式的松弛模型能较好地反映松弛曲线前期快速下降阶段的特征,从数学表达式上看,当时间t取无穷大时,偏应力最终会趋近于负无穷,但是在工程寿命范围内该函数是适合的,而时间t无穷大在工程实践中无太大实际意义。因此,选取幂函数作为松弛模型具有工程实际意义。
(3) 本次研究仅完成了净围压为100kPa、基质吸力ua=50,100,150,200,250kPa的5个松弛试验,试验数量有限,文中所建立的松弛模型能否推广还需更多试验验证。
参考文献:
[1]孙广忠.中国典型滑坡[M].北京:科学出版社,1998.
[2]李翠华,侍倩,李百鸣.饱和软粘土松弛特性试验研究及模型建立[J].土工基础,2001, 15(3): 38-40.
[3]尹清杰,王世梅.饱和土松弛实验曲线模拟与试验验证[J].黑龙江水专学报,2006, 33(2): 24-26.
[4]肖宏彬,范志强,张春顺,等.性流变特性试验研究[J].公路工程,2009,34(2):2-5.
[5]王琛,詹传妮.堆石料的三轴松弛试验[J].四川大学学报(工程科学版),2011,43(1):27-30.
[6]李孝平,王世梅,李晓云,等.GDS三轴仪的非饱和土试验操作方法[J].三峡大学学报(自然科学版),2008,30(5): 37-40.
[7]王世梅,刘德富,陈勇,等. 某滑坡滑带非饱和土强度特性试验研究[J].合肥工业大学学报(自然科学版),2005,28(12): 1578-1581.
[8]李佳川.土的流变模型及应力松弛[J].岩土工程师,1990,2(4):27-31.
(编辑:赵卫兵)
Study on Unsaturated Relaxation Properties of Soils of a Landslidein the Three Gorges Reservoir Area and Model Construction
LIUJia-long1,2,WANGShi-mei1,2,HUQiu-fen1,2,GUOZhen2
(1.CollaborativeInnovationCenterforGeo-hazardsandEco-environmentinThreeGorgesArea,Yichang443002,China;2.CollegeofCivilEngineering&Architecture,ChinaThreeGorgesUniversity,
Yichang443002,China)
Abstract:In order to obtain influence of matric suction on relaxation properties of unsaturated soil, we conduct stress relaxation tests of unsaturated soil of a landslide in Three Gorges Reservoir area by using GDS triaxial apparatus. Exponential function, logarithmic function and power function are selected for curve fitting. Through comparative analysis, power function is selected as the relaxation model as it has maximum fitting accuracy, and the model parameters under different matric suctions are obtained. The correlations between matric suctions and model parameters are analyzed, and function relationships are built. The function relationships are substituted into the relaxation model equation and a relaxation model that can reflect the effect of matric suction of unsaturated soil is obtained.
Key words:landslide; unsaturated soil; matric suction; relaxation model;relaxation properties
收稿日期:2015-03-10;修回日期:2015-04-07
基金项目:国家自然科学基金项目(41372359)
作者简介:刘佳龙(1990-),男,湖北孝感人,硕士研究生,主要从事岩土体稳定性方面的研究,(电话)18871730681(电子信箱)190222591@qq.com。 通讯作者:王世梅(1965-),女,湖北宜昌人,教授,博士生导师,主要从事非饱和土流变特性研究,(电话)13972598072(电子信箱)284480957@qq.com。
doi:10.11988/ckyyb.20150170
中图分类号:P642.22
文献标志码:A
文章编号:1001-5485(2016)06-0079-04
2016,33(06):79-82
