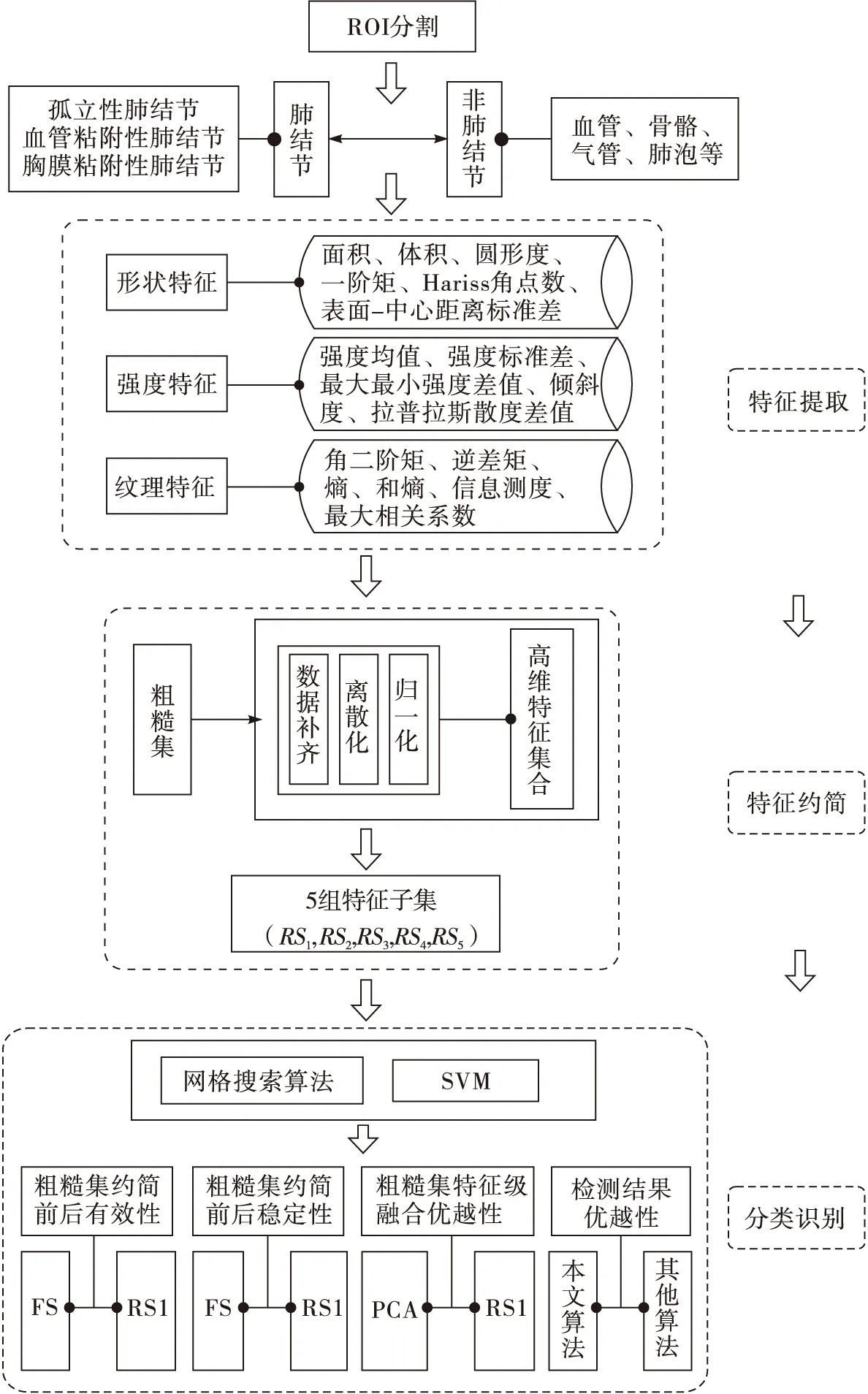
基于粗糙集特征级融合的肺结节检测算法
2016-06-24张俊杰王文文
张俊杰,周 涛,夏 勇,王文文
(1.宁夏医科大学 a.管理学院;b.理学院,宁夏 银川 750004;2.西北工业大学 计算机学院,陕西 西安 710100)
基于粗糙集特征级融合的肺结节检测算法
张俊杰1a,周涛1b,夏勇2,王文文1a
(1.宁夏医科大学a.管理学院;b.理学院,宁夏 银川 750004;2.西北工业大学计算机学院,陕西 西安 710100)
摘要:以肺结节的检测为研究目标,针对肺结节特征级融合检测算法中存在特征结构不合理和特征表达不紧致两个问题,提出了一种基于粗糙集特征级融合的肺结节检测算法,该算法首先分析肺部CT影像的医学征象,提出了六个新的三维特征,并综合其他二维和三维特征共42维特征分量共同量化ROI;然后基于粗糙集对提取的特征集合进行5次特征级融合实验;最后利用网格寻优算法优化核函数的SVM作为分类器进行肺结节识别。以70例肺结节患者的肺部CT影像为原始数据,通过4组对比实验验证算法的有效性和稳定性,实验结果表明,经过粗糙集特征级融合的肺结节检测算法识别肺结节的能力得到了有效提升。
关键词:肺结节检测;粗糙集;特征提取;特征约简;支持向量机
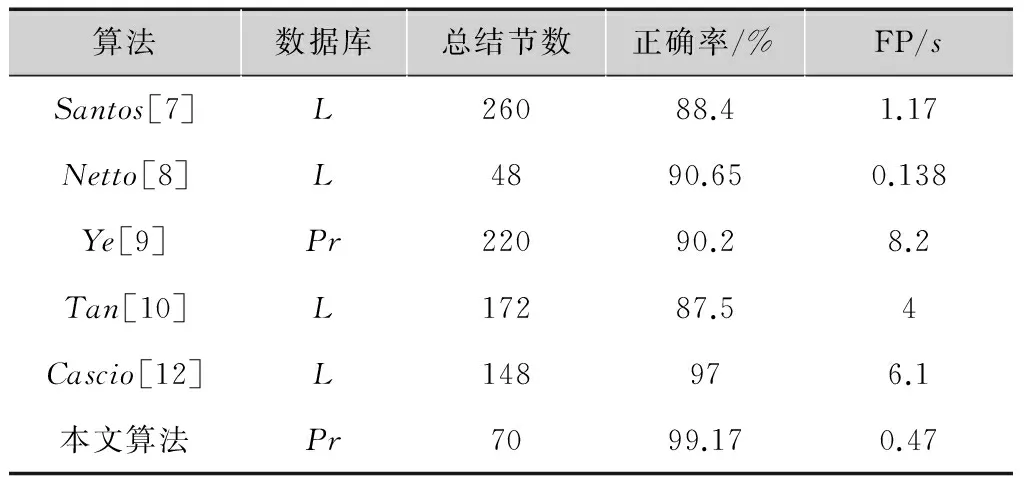
肺癌已成为世界范围内发病率及死亡率最高的恶性肿瘤,严重威胁着人类的生命健康[1-2],早期发现是提高肺癌患者治疗效果的有效方法[3],同时由于肺结节(lungnodules)是肺癌的早期形态[4],因此肺结节的检测识别在肺癌治疗中的重要性日益凸显。计算机断层扫描成像(ComputedTomography,CT)为临床诊断提供了多角度、可视化、高质量的胸部医学影像[4],但是随着CT在肺结节检测中的广泛应用,产生的CT数据过载以及影像结果判读主观性等因素,都导致临床误诊率居高不下[5]。计算机辅助诊断(Computer-AidedDiagnosis,CAD)能够对海量CT影像数据进行前期筛查、标记可疑病灶区域,然后结合影像医生的二次判别在降低其阅片工作量的同时提高肿瘤诊断正确率[6],是解决上述问题的有效渠道之一。
肺结节检测是CAD研究的热点之一,如Santos[7]等首先基于区域生长法分割出肺实质,并根据高斯混合模型和海森矩阵从肺实质中分离出ROI,然后选取Tsallis熵和香农熵作为描述特征,利用支持向量机(SupportVectorMachine,SVM)对肺结节和非结节区域进行分类识别;Netto[8]等首先利用增长型神经气体(GrowingNeuralGas,GNG)进行聚类粗分割,然后根据三维距离变换把肺结节从含有血管、支气管的组织中分离出来,最后利用SVM在提取的形状特征和纹理特征集合的基础上实现对肺结节的有效识别;Ye[9]等首先综合模糊阈值、高斯矩阵、平均曲率、海森矩阵等算法进行ROI的分割提取,然后选用局部形状特征和局部散度信息作为ROI的特征表达,最后采用加权的SVM进行肺结节的识别检测;Tan[10]等首先基于Li[11]等提出的血管和结节增强滤波器进行肺结节的分割,然后根据基于高斯模板计算的散度定位肺结节的聚类中心,实现ROI的提取,最后采用基于遗传算法的分类器、人工神经网络(ArtificialNeuralNetworks,ANN)、SVM三种分类器对比分析肺结节的检测效果;Cascio[12]等首先利用区域增长算法和形态学操作提取出ROI,然后基于3D弹簧模型进行样条曲面重建,以便于提取相关的三维灰度特征和形状特征,最后采用ANN进行肺结节的检测。虽然以上文献对肺结节的检测方法进行了一定的探讨,但整体来看,这些方法在特征结构的设计和特征集合的表达方面还存在以下不足:
1)提取特征集合量化ROI时,存在特征结构设计不合理的问题,较少考虑全局特征和局部特征、二维特征和三维特征的结合,并且容易忽视特征分量刻画的准确性。
2)特征数据融合时,特征表达的紧致性是一个棘手的问题,较少考虑剔除特征冗余、保留有效特征,而且无需先验知识的特征级融合方法很少被应用。
基于以上原因,本文提出了一种基于粗糙集(RoughSets,RS)特征级融合的肺结节检测算法。针对第一个问题,提取了形状特征、强度特征和纹理特征,其中在形状特征中,提出了3个新的三维特征,即外接球形体积比、表面-中心距离标准差和外接长方体交线距离;在强度特征中,提出了3个新的三维特征,即强度梯度(由内向外)、拉普拉斯散度均值、拉普拉斯散度距离;在特征描述上,使用二维纹理特征和三维形状特征、强度特征共同量化;针对第二个问题,充分考虑粗糙集无需先验知识和能够充分保留特征属性的特点,采用粗糙集进行特征级融合,最后采用网格寻优算法优化SVM核函数并进行肺结节的识别检测。为了验证本文算法的有效性、稳定性、优越性,本文做了4组对比实验,即粗糙集约简前后的算法有效性验证实验、粗糙集约简前后的算法稳定性验证实验、基于粗糙集特征级融合算法的优越性验证实验、与其他肺结节检测算法的性能对比实验,实验结果表明,该算法能够在一定程度上提升特征结构的合理性和特征表达的紧致性,从而提高肺结节的检测正确率。
1相关理论
1.1CT肺结节ROI的特征分析及量化
ROI特征由其描述的全面性(即特征分量的维度,过少的特征描述量无法以“多视角”的方式“观测”病灶的特性)和刻画的准确性(即反映特征真实性的程度,特征量化数值偏离真实信息较多会造成特征区分度过低)共同影响,大量的噪声信息会降低ROI的特征提取精度,影响最终的检测结果,因此,为全面、准确地表达肺结节ROI的形态结构、局部特性,本文在对肺结节ROI医学征象分析的基础上,提出6个新的三维特征,并结合其他形状特征、强度特征、纹理特征分别从二维和三维角度对病灶进行定性分析和定量刻画。
1.1.1形状特征
形状特征是最直观的视觉特征,能够从几何形状、边缘粗糙度、拓扑结构等角度表示CT肺结节ROI的圆形肿块征、分叶征、棘状突起征、空泡征、毛刺征等主要医学征象,本文提取的形状特征分量主要有:周长、面积、体积、圆形度、矩形度、伸长度、欧拉数、外接球形体积比、表面-中心距离标准差、角点数、Hu矩,外接长方体交线距离。
其中:外接球形体积比是三维CT影像所提取的每个ROIAi(最大直径是dim(Ai))与其外接球形体积VS(Ai)的比值,反映了该区域与球形的相似度,如图1b所示。
(1)
(2)
表面-中心距离标准差,是ROI表面每个体素C(Si)与区域中心Ccen(Ai)的坐标距离标准差,其值同样描述了ROI的类球性,如果E2(Ai)的值为0,则该区域是一个标准的球形,随着E2(Ai)的值增大,则该区域偏离球形的幅度随之增大,如图1c所示。
(3)
外接长方体交线距离,是ROI中心体素Ccen(Ai)与其外接长方体6个切面的12条交线中心dim(Li)(i=1,2,…,12)的距离,可以表示该区域体素在矩形体中均匀分布的程度,如图1d所示。
(4)
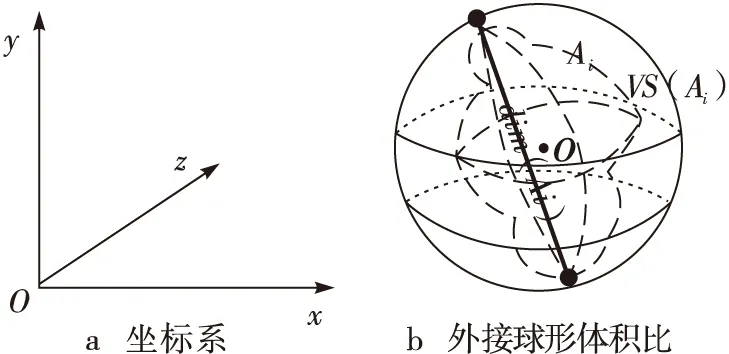
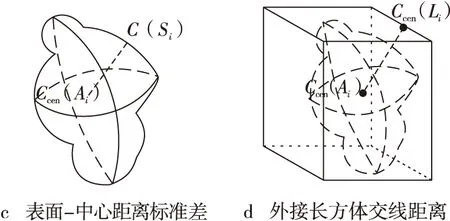
图1 三维特征示意图
1.1.2强度特征
灰度统计特征是用定量的方法描述二维图像区域的最基本特征,从三维角度考虑称之为强度特征[12],本文提取的强度特征分量有强度均值、强度方差、最大最小强度差值、偏斜度、峰度、强度梯度(由内向外)、拉普拉斯散度(均值、差值)。
其中:强度梯度(由内向外),对ROIAi中体积大于0的体素Si不断地做形态学腐蚀处理,求得每一次腐蚀剔除面的均值与上一次操作的均值作比较(初始为0),直到体积为零,如果比值为正,则k=k+1(初始为0),其中n是腐蚀操作的次数。
(5)
拉普拉斯散度均值,根据拉普拉斯算子La与原始CT影像卷积后的结果发现,结节周围灰度值差异较小的区域其散度却有明显的不同,因此,计算拉普拉斯散度有利于区分肺结节与干扰杂质。
E5(Ai)=mean(Ai×La)
(6)
拉普拉斯散度距离,拉普拉斯散度的最大值与最小值的差值,描述了区域散度的变化范围。
E6(Ai)=max(Ai×La)-min(Ai×La)
(7)
1.1.3纹理特征
强度特征描述了体素灰度级分布的相关信息,基于统计法的纹理特征是从间隔等距离的空间像素间变化关系刻画肺结节ROI的潜在特征,本文提取了基于灰度共生矩阵(Gray-LevelCo-occurrenceMatrix,GLCM)的角二阶矩、惯性矩、逆差矩、和均值、方差、和方差、差分方差、熵、熵的和、差分熵、信息测度、相关系数、最大相关系数[5],基于Tamura纹理特征的粗糙度、对比度、方向度。
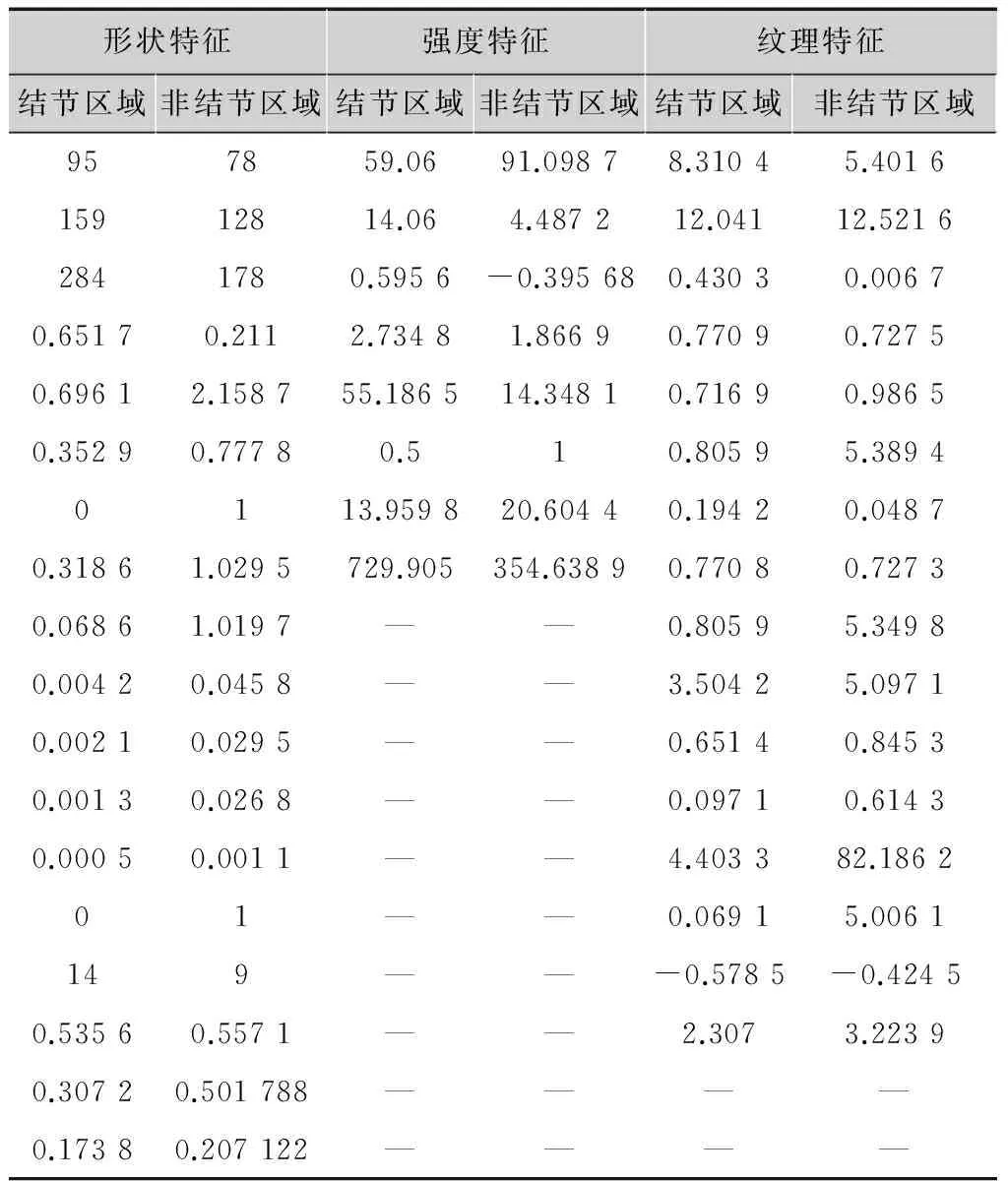
基于以上对肺结节ROI的特征描述分析,表1给出了提取的42维特征分量集合,为便于后续测试,按表1中的书写顺序对其依次进行编号,其中形状特征编号依次为fs1~fs18;强度特征编号依次为fi1~fi8;纹理特征编号依次为ft1~ft16。
表1CT肺结节ROI特征集合

特征类别特征分量维度形状特征周长、面积、体积、圆形度、矩形度、伸长度、欧拉数、角点数、Hu矩(一阶矩、二阶矩、三阶矩、四阶矩、五阶矩、六阶矩、七阶矩)、外接球形体积比、表面-中心距离标准差、外接长方体交线距离18强度特征灰度均值、灰度方差、偏斜度、峰度、最大最小灰度差值、强度梯度(由内向外)、拉普拉斯散度均值、拉普拉斯散度差值8纹理特征Tamura纹理特征(粗糙度、对比度、方向度)、GLCM(角二阶矩、惯性矩、逆差矩、和均值、方差、和方差、差分方差、熵、熵的和、差分熵、信息测度、相关系数、最大相关系数)16
1.2粗糙集属性约简
医学影像的特征分析有助于人为预判选取何种特征才能对ROI进行最有效的特征表达,但当考虑采用高维特征集合全面刻画ROI时,人为选取特征描述的主观性会造成特征分量信息交叉,使分类算法的性能难以到达最优效果,剔除信息冗余的特征分量有利于构建更具适用性、紧致性的肺结节检测模型,因此,有效的特征降维是解决以上问题的有效途经。主成分分析(PrincipalComponentAnalysis,PCA)作为通过特征变换的形式实现特征降维的常用方法,是把所有的特征分量作为一个整体进行最优线性投影,并不注重类别属性的区分度,这种忽视掩盖了非优投影方向所存在的重要可分性信息,为弥补这种不足,本文采用粗糙集模型进行属性约简,降低特征维度。
粗糙集作为一种刻划不确定性和不完整性的软计算数学工具,其特点是无需特征集合的先验知识描述,而是直接从问题的分类知识出发,在保持较高分类能力的情况下,通过不可分辨关系导出问题的约简结果。其数学定义如下:
设S=(U,A,V,F)为一信息系统,其中论域U={x1,x2,…,xn},A是属性集合,V是属性值集合,F是U中对象的属性与其属性值的关系映射:U×A→V。
定义1令R={r1,r2,r3,…,rn},且r≠φ,则∩r也是一个等价关系,IND(r)称为r上的不可分辨关系,即
IND(r)={(xi, xj)∈U×U|f(xi, r)=f(xj, r) }
定义2对于任一子集ri∈R,如果IND{R-{ri}}=IND(R),则称ri是可以约简掉的。通常基于粗糙集的属性约简并不是唯一的,即可能存在多个约简子集。
定义3若R划分为条件属性C和决策属性D,则C∪D=R,C∩D=φ,当D以依赖度K(0≤k≤1)依赖于C,记为C=>KD。
1.3支持向量机及其优化
SVM是一种基于统计理论的有监督学习模型,其主要思想是利用给定的训练样本构造最佳分类超平面,使距离超平面最近的不同类别元素之间的距离最大化。SVM具有学习性能优、训练时间短、选择参数少、泛化能力强、拟合精度高等优点,能够解决线性可分和线性不可分的问题,常被用于目标检测,模式识别[13-14]。SVM的优化函数和分类函数为
(8)
(9)
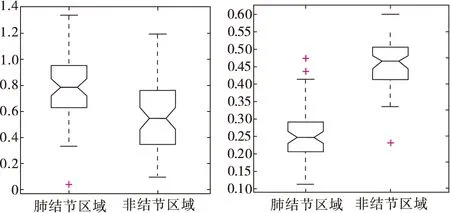
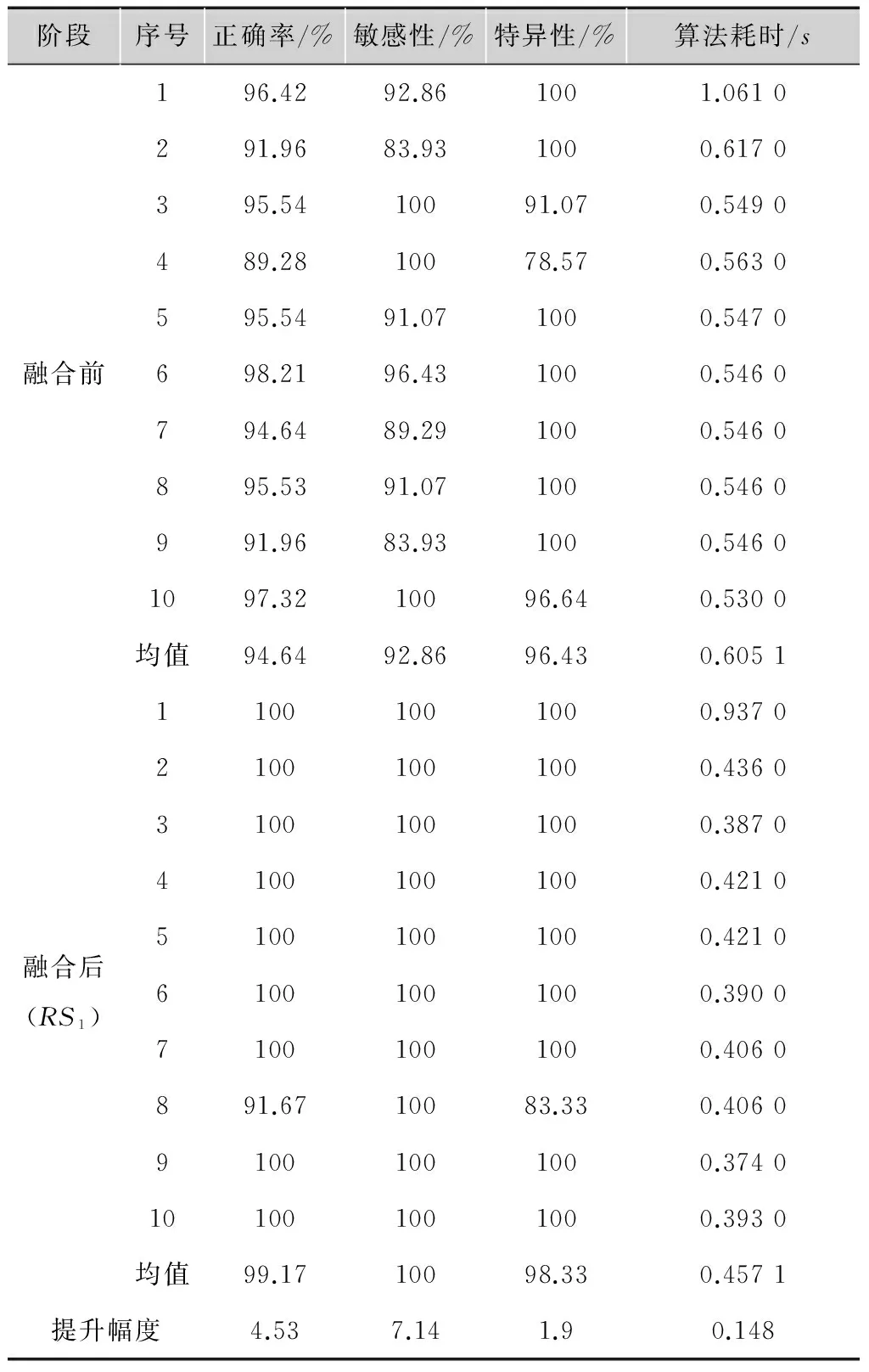
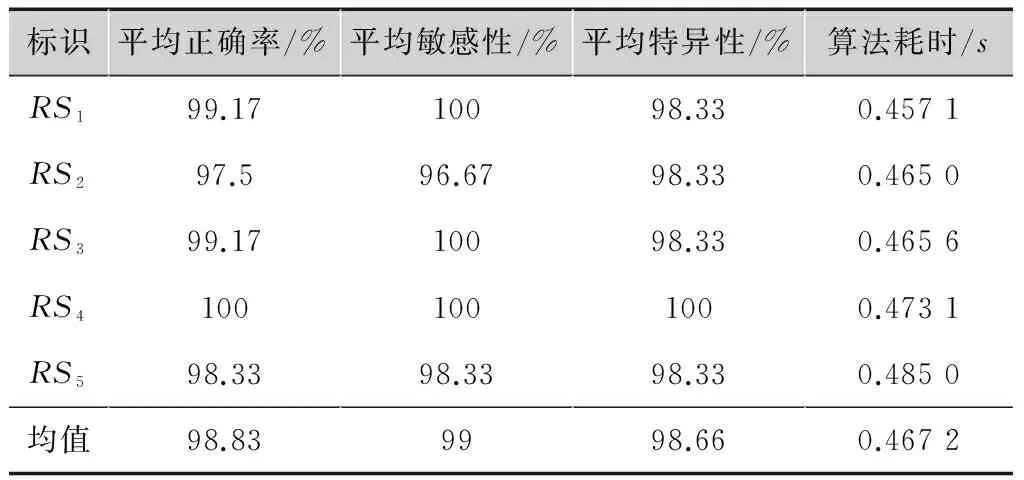
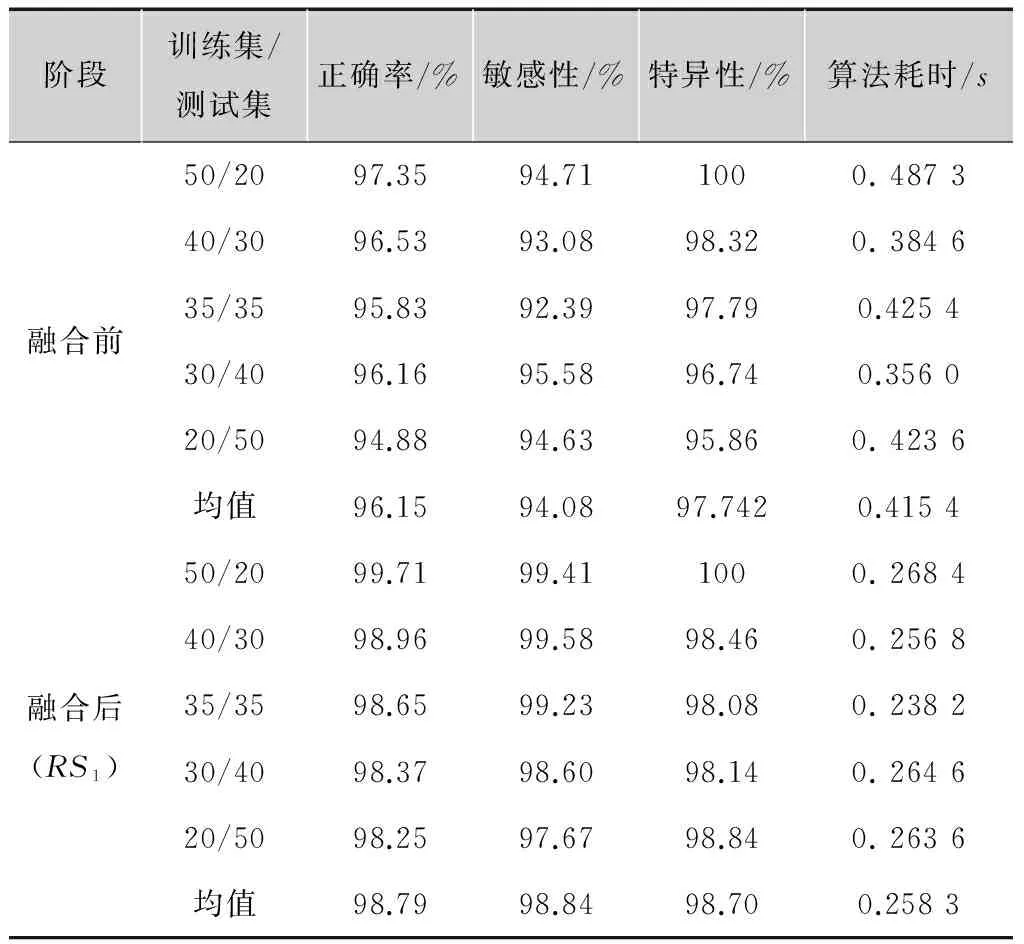
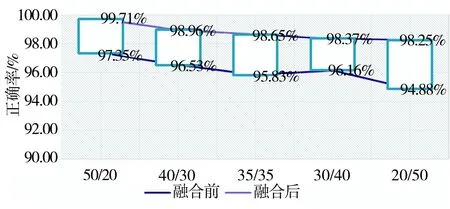
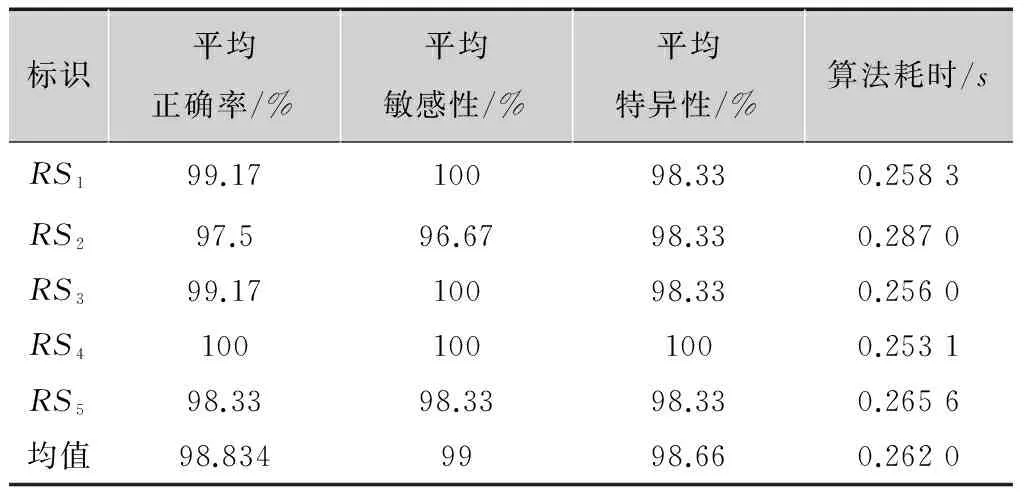
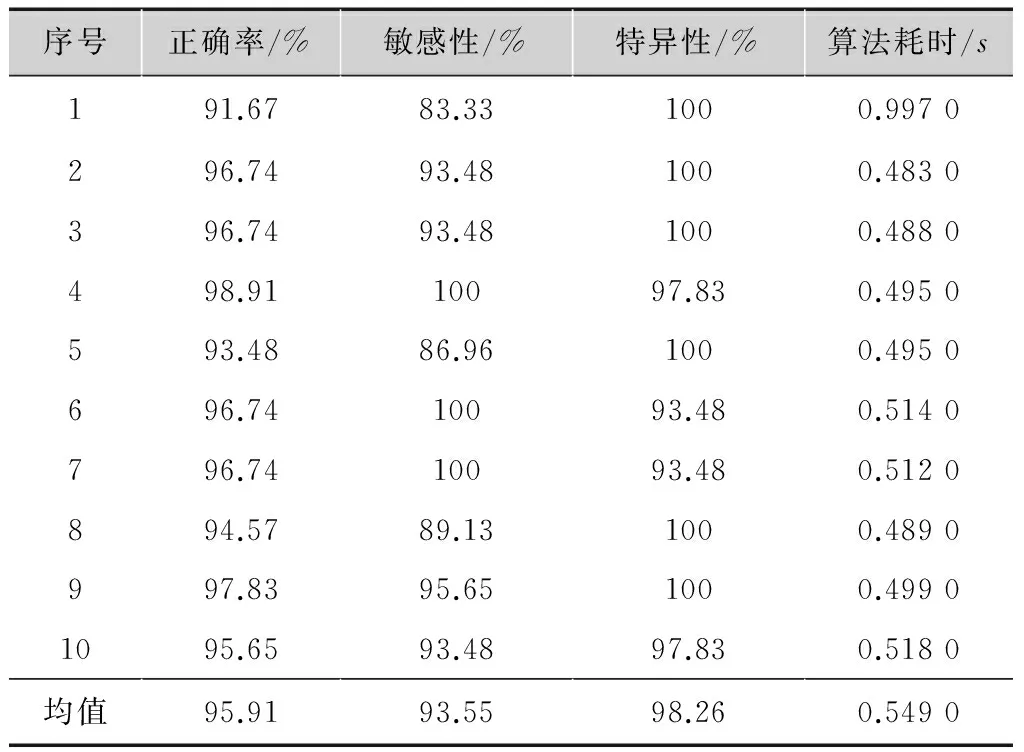
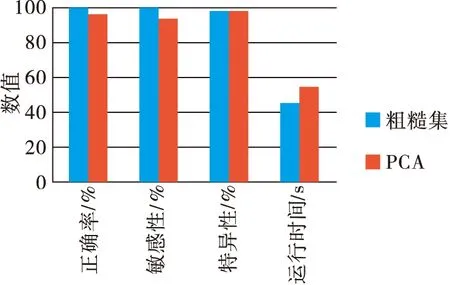
其中,0 (10) 惩罚系数C和核函数的参数g对SVM的分类性能有极其重要的影响,为了得到最优分类结果,本文选用网格寻优算法对其进行优化。网格寻优算法是在一定的空间范围中以网格的形式表示待搜索参数,并通过遍历网格中所有的点来寻找最优参数,具有简单方便、稳定性好、易于找出全局最优解的优点[15]。在SVM学习过程中,采用十折交叉验证计算出分类性能最优的核函数参数和惩罚系数,然后把优选结果应用于SVM分类器进行肺结节的识别检测,最后选用检测敏感性、特异性、正确率、算法耗时作为相关实验的评价指标。 2本文算法 本文选用70例肺结节患者的CT影像作为研究样本,首先分割提取出经过影像科医生标记的3种不同类型的肺结节(孤立性肺结节、血管粘附性肺结节、胸膜粘附性肺结节)以及大量的非肺结节区域(血管、骨骼、肺泡等),分别从二维和三维角度提取出刻画ROI的形状特征18维,强度特征8维,纹理特征16维,共计42维特征分量(包括本文所提的6个新的三维特征);然后对提取的特征集合(标识为FS)进行数据补齐、离散化、归一化处理,利用粗糙集模型对完善的特征数据进行5次特征级融合(由于特征约简子集不唯一,本文对提取的特征集合进行5次约简,分别标识为RS1,RS2,RS3,RS4,RS5),选用其中的一组特征子集(RS1)作为以下对比实验最主要的实验测试组;最后采用网格寻优算法优化SVM参数,并将改进的SVM主要应用于设定的4组对比实验,分别对比分析粗糙集约简前后的特征分类有效性及稳定性、基于粗糙集和基于PCA的特征级融合的识别性能、本文肺结节检测算法和其他文献肺结节检测算法的识别性能。基于以上算法思想,图2给出了基于粗糙集特征级融合的肺结节检测算法流程图。 图2 基于粗糙集特征级融合的肺结节检测流程图 3仿真实验 3.1实验环境 本文实验所涉及的软、硬件环境如下: 软件环境:Windows7操作系统,MatlabR2014b,ImageJ1.48u,LibSVM。 硬件环境:IntelCorei5 4670-3.4GHz,8.0Gbyte内存,500Gbyte硬盘。 实验数据:采用经过影像科医生标记的70例肺结节患者的CT图像(共2 232幅,其中孤立性肺结节38例,血管粘附性肺结节17例,胸膜粘附性肺结节15例)作为实验样本,大小均为512×512,厚度为2mm。图3给出了3种不同类型的肺结节以及对应的肺结节分割结果。 图3 肺结节分割结果 本文对标记的70个非结节区域和随机抽样的70个非肺结节区域分别提取了42维特征,表2给出了肺结节区域和非肺结节区域的42维特征值,为了能够直观了解不同特征的特征值分布情况和区分度对比,图4给出了肺结节区域和非肺结节的外接球形体积比和表面-中心距离标准差的箱线图。 3.2实验一:基于粗糙集的特征级融合 为避免小数值范围的属性值被大数值范围的属性值所支配,同时降低统计计算过程中的复杂度,首先对提取的特征集合进行数据预处理(规范化差异性较大的数据,并将数据线性映射到[0,1]之间),然后采用粗糙集模型进行5次特征数据融合,融合结果如表3所示。 3.3实验二:基于网格寻优的SVM肺结节检测 1)粗糙集约简前后的算法有效性验证实验 本文采用十折交叉验证法分别计算特征集约简 表2结节区域和非结节区域的特征值 形状特征强度特征纹理特征结节区域非结节区域结节区域非结节区域结节区域非结节区域957859.0691.09878.31045.401615912814.064.487212.04112.52162841780.5956-0.395680.43030.00670.65170.2112.73481.86690.77090.72750.69612.158755.186514.34810.71690.98650.35290.77780.510.80595.38940113.959820.60440.19420.04870.31861.0295729.905354.63890.77080.72730.06861.0197——0.80595.34980.00420.0458——3.50425.09710.00210.0295——0.65140.84530.00130.0268——0.09710.61430.00050.0011——4.403382.186201——0.06915.0061149——-0.5785-0.42450.53560.5571——2.3073.22390.30720.501788————0.17380.207122———— a 外接球形体积比的箱线图 b 表面-中心距离标准差的箱线图 子集标识约简结果维数RS1fs4,fs16,fs17,fs18,fi2,fi4,fi6,fi7,fi8,ft2,ft4,ft5,ft6,ft7,ft8,ft9,ft10,ft11,ft13,ft14,ft15,ft1621RS2fs4,fs9,fs16,fs18,fi1,fi2,fi5,ft2,ft5,ft6,ft8,ft9,ft10,ft11,ft12,ft13,ft1517RS3fs9,fs17,fs18,fi1,fi2,fi5,fi7,fi8,ft2,ft6,ft7,ft8,ft9,ft10,ft11,ft12,ft14,ft15,ft1619RS4fs9,fs16,fs18,fi1,fi2,fi5,fi7,fi8,ft5,ft6,ft7,ft8,fy9,ft10,ft11,ft12,ft14,ft15,ft1619RS5fs9,fs16,fs17,fs18,fi1,fi2,fi4,fi5,fi7,fi8,ft2,ft5,ft6,ft7,ft8,ft9,ft10,ft12,ft15,ft1620 表4融合前后算法有效性统计表 阶段序号正确率/%敏感性/%特异性/%算法耗时/s融合前196.4292.861001.0610291.9683.931000.6170395.5410091.070.5490489.2810078.570.5630595.5491.071000.5470698.2196.431000.5460794.6489.291000.5460895.5391.071000.5460991.9683.931000.54601097.3210096.640.5300均值94.6492.8696.430.6051融合后(RS1)11001001000.937021001001000.436031001001000.387041001001000.421051001001000.421061001001000.390071001001000.4060891.6710083.330.406091001001000.3740101001001000.3930均值99.1710098.330.4571提升幅度4.537.141.90.148 前后(粗糙集约简后的数据集采用实验一得到的RS1(70×21)的分类正确率、敏感性、特异性、算法耗时等四个指标对比分析两者肺结节的分类识别性能,结果如表4所示。 实验结果表明,经过特征级融合后的肺结节检测正确率有明显提高,同时降低了漏诊率(敏感性提升表明肺结节检测中出现假阴性的概率降低)和误诊率(特异性提升表明肺结节检测中出现假阳性的概率降低),算法耗时也有所缩减,这说明粗糙集约简模型在本文提取的42维特征集合上进行特征级融合是有效的,不仅提升了特征集的紧致度(消除了特征冗余和低区分度特征分量),也修正了特征集合中的异常数据,进一步提高了肺结节的检测性能。表5给出了5组粗糙集约简子集的有效性统计表。 2)粗糙集约简前后的算法稳定性验证实验 本文以不同的训练、测试比例(50/20、40/30、35/35、30/40、20/50)对肺结节特征数据(粗糙集约简后的数据集采用实验一得到的RS1(70×21))进行5轮分类检测,每轮样本根据设定的训练、测试比例进行随机抽取,统计10次测试结果的均值作为对应的正确率、敏感性、特异性、算法耗时,对比结果如表6所示。 表5粗糙集约简子集有效性统计表 标识平均正确率/%平均敏感性/%平均特异性/%算法耗时/sRS199.1710098.330.4571RS297.596.6798.330.4650RS399.1710098.330.4656RS41001001000.4731RS598.3398.3398.330.4850均值98.839998.660.4672 表6算法稳定性统计表 阶段训练集/测试集正确率/%敏感性/%特异性/%算法耗时/s融合前50/2097.3594.711000.487340/3096.5393.0898.320.384635/3595.8392.3997.790.425430/4096.1695.5896.740.356020/5094.8894.6395.860.4236均值96.1594.0897.7420.4154融合后(RS1)50/2099.7199.411000.268440/3098.9699.5898.460.256835/3598.6599.2398.080.238230/4098.3798.6098.140.264620/5098.2597.6798.840.2636均值98.7998.8498.700.2583 实验结果表明,随着训练集与测试集的比率下降,粗糙集约简子集分类正确率的下降趋势并不明显,而约简前的分类正确率却出现了一定的波动(图5给出了更为直观的展示),这说明本文提出的基于粗糙集的特征级融合算法的分类稳定性较高,不易受到样本数据量单薄的干扰,表7给出了5组粗糙集约简子集的稳定性统计表。 图5 约简前后检测正确率走势对比图 表7 5组粗糙集约简子集分类对比表 3)基于粗糙集特征级融合算法的优越性验证实验 由于PCA算法发展成熟,计算简便,易于编程实现,所以也成为大多数特征级融合的首选降维方法,为对比分析两种特征级融合算法的对比度,本文对所提特征集合同时进行了基于PCA的特征级融合,十折交叉验证的各项指标结果如表8所示,图6给出了这两种特征级融合算法的分类性能对比图(粗糙集约简子集的有效性数据采用表3中RS1的验证结果,为便于观察,图6中将算法耗时放大了100倍)。 表8PCA约简子集有效性统计表 序号正确率/%敏感性/%特异性/%算法耗时/s191.6783.331000.9970296.7493.481000.4830396.7493.481000.4880498.9110097.830.4950593.4886.961000.4950696.7410093.480.5140796.7410093.480.5120894.5789.131000.4890997.8395.651000.49901095.6593.4897.830.5180均值95.9193.5598.260.5490 图6 两种特征级融合算法的对比图 实验结果表明,基于粗糙集特征级融合算法的各项性能指标均优于基于PCA的特征级融合算法,这说明粗糙集比PCA更适用于消除本文所提特征的冗余信息。 4)与其他肺结节检测算法的性能对比实验 这里同时采用检测正确率和单层切片误检率(FalsePositivesperscan,FP/s)作为肺结节检测算法的评价指标,将本文算法与其他三种肺结节检测算法的评价指标(肺结节检测算法的正确率均采用最优检测正确率)进行对比分析,结果如表9所示(Pr:非公开数据库;L:LIDC)。 表9肺结节检测算法对比表 算法数据库总结节数正确率/%FP/sSantos[7]L26088.41.17Netto[8]L4890.650.138Ye[9]Pr22090.28.2Tan[10]L17287.54Cascio[12]L148976.1本文算法Pr7099.170.47 实验结果表明,本文提出的肺结节检测算法在一定程度上优于其他肺结节检测算法的识别检测性能,这说明本文不仅通过补充、改进特征分量提高了CT肺结节ROI的特征描述的全面性和刻画的准确度,而且结合粗糙集特征级融合的思想剔除了冗余特征和特征数据中的不规则信息,提升了特征集合的紧致度,从而提高了整体的肺结节检测性能。 4小结 本文从CT影像的肺结节检测出发,分析了肺结节检测算法的研究现状,提出了一种基于粗糙集特征级融合的肺结节检测算法。该算法针对特征提取过程中的特征描述不充分、刻画不准确问题,提出了六个新的三维特征,并结合其他二维、三维特征共同提取、量化ROI的特征信息,但提取的高维特征集合存在特征信息交叉的问题,本文利用粗糙集进行特征级融合,降低了特征集合的维度,采用网格寻优算法优化SVM核函数,并以此分类器进行检测识别,最后采用4组对比实验验证本文算法的肺结节检测性能。实验结果表明,基于粗糙集的特征级融合肺结节检测算法是有效的,该算法的分类正确率基本能够满足医学影像学对肺结节的检测识别要求,对于肺结节的检测以及肺癌的辅助诊断研究具有重要的价值。 参考文献: [1]RIAZSP,LüCHTENBORGM,COUPLANDVH,etal.Trendsinincidenceofsmallcelllungcancerandalllungcancer[J].Lungcancer,2012,75(3):280-284. [2]FERLAYJ,SOERJOMATARAMI,DIKSHITR,etal.Cancerincidenceandmortalityworldwide:sources,methodsandmajorpatternsinGLOBOCAN2012[J].InternationalJournalofCancer,2015,136(5): 359-386. [3]BALDWINDR.Predictionofriskoflungcancerinpopulationsandinpulmonarynodules:Significantprogresstodrivechangesinparadigms[J].Lungcancer,2015,89(1):1-3. [4]DICIOTTIS,PICOZZIG,FALCHINIM,etal. 3-DsegmentationalgorithmofsmalllungnodulesinspiralCTimages[J].IEEEtransactionsoninformationtechnologyinbiomedicine, 2008,12(1):7-19. [5]THEODORIDISS,KOUTROUMBASK.Patternrecognition[M]. 李晶皎,王爱侠,王娇,译.北京:电子工业出版社, 2010. [6]SAHINERB,CHANHP,HADJIISKILM,etal.EffectofCADonradiologists'detectionoflungnodulesonthoracicCTscans:analysisofanobserverperformancestudybynodulesize[C]//Proc.ofSPIE. [S.l.]:IEEEPress,2009,16(12):1518-1530. [7]SANTOSAM,FILHOAODC,SILVAAC,etal.Automaticdetectionofsmalllungnodulesin3DCTdatausingGaussianmixturemodels,TsallisentropyandSVM[J].Engineeringapplicationsofartificialintelligence,2014(36):27-39. [8]NETTOSMB,SILVAAC,NUNESRA,etal.Automaticsegmentationoflungnoduleswithgrowingneuralgasandsupportvectormachine[J].Computersinbiologyandmedicine,2012,42(11):1110-1121. [9]YEX,LINX,DEHMESHKIJ,etal.Shape-basedcomputer-aideddetectionoflungnodulesinthoracicCTimages[J].IEEEtransactionsonbiomedicalengineering,2009,56(7):1810-1820. [10]TANM,DEKLERCKR,JANSENB,etal.Anovelcomputer-aidedlungnoduledetectionsystemforCTimages[J].Medicalphysics,2011,10 (38):5630-5645. [11]LIQ,LIF,DOIK.Computerizeddetectionoflungnodulesinthin-sectionCTimagesbyuseofselectiveenhancementfiltersandanautomatedrule-basedclassifier[J].Academicradiology,2008,15(2):165-175. [12]CASCIOD,MAGROR,FAUCIF.AutomaticdetectionoflungnodulesinCTdatasetsbasedonstable3Dmass-springmodels[J].Computersinbiologyandmedicine,2012,42: 1098-1109. [13]RAJAR,DUTTAA,VENKATESHKS.Newpotentialfieldmethodforroughterrainpathplanningusinggeneticalgorithmfora6-wheelrover[J].Roboticsandautonomoussystems,2015,72:295-306. [14]CHENGD,WANGJJ,WEIX,etal.TrainingmixtureofweightedSVMforobjectdetectionusingEMalgorithm[J].Neurocomputing,2015,149(B):473-482. [15]CHOROWSKIJ,WANGJ,ZURADAJM.ReviewandperformancecomparisonofSVM-andELM-basedclassifiers[J].Neurocomputing,2014,128:507-516. 责任编辑:闫雯雯 Lungnodulesdetectionbasedonroughsetsatfeaturelevel ZHANGJunjie1a,ZHOUTao1b,XIAYong2,WANGWenwen1a (1a.College of Management;1b.School of Science, Ningxia Medical University, Yinchuan 750004, China;2.School of Computer Science, Northwestern Polytechnical University, Xi’an 710100, China) Abstract:Based on the detection of lung nodules as the research target, in terms of the two problemsof lung nodules detection algorithmat the feature level fusionthat features structure is not reasonable and feature expression is not tight, a lung nodule detection algorithm based on rough setsat feature level fusion is proposed.The algorithm firstly analyze medical signs of lung CT image, six new 3d characteristics are proposed, and other 2d and 3d features as a total of 42 features quantitative ROI; then based on rough sets to extract the feature sets for 5 times experiments; at last the grid optimization algorithm is used to optimize the kernel function of SVM as classifier to identify the lung nodules. Based on 70 cases of lung nodules in patients with lung CT images as the original data, through four groups of experiments verify the validity and stability of the algorithm, and the experimental results show that after the lung nodules detection algorithm of rough set feature level fusion effectively improved the recognition ability of lung nodules. Key words:lung nodules detection; rough sets; feature extraction; feature reduction; SVM 中图分类号:TN911.73 文献标志码:A DOI:10.16280/j.videoe.2016.03.028 基金项目:国家自然科学基金项目(81160183;61561040);宁夏自然科学基金项目(NZ12179;NZ14085);宁夏高等学校科研项目(NGY2013062) ;陕西省语音与图像信息处理重点实验室开放课题资助项目(SJ2013003) 收稿日期:2015-10-19 文献引用格式:张俊杰,周涛,夏勇,等. 基于粗糙集特征级融合的肺结节检测算法[J].电视技术,2016,40(3):130-137. ZHANGJJ,ZHOUT,XIAY,etal.Lungnodulesdetectionbasedonroughsetsatfeaturelevel[J].Videoengineering, 2016,40(3):130-137.