基于新UNIFAC基团的尼龙66盐溶解度的计算方法

顾雪萍，田璐璐，冯连芳，张才亮（浙江大学化学工程联合国家重点实验室，浙江 杭州 310027）

基于新UNIFAC基团的尼龙66盐溶解度的计算方法

顾雪萍，田璐璐，冯连芳，张才亮
（浙江大学化学工程联合国家重点实验室，浙江 杭州 310027）

摘要：尼龙66（PA66）盐在水中溶解度的准确计算是尼龙66聚合过程模型化基础。选择UNIFAC活度系数方法，针对PA66聚合体系对组分进行基团划分，定义的新基团为羧基和氨基形成的缔合基团（—CH2COO−·+H3NCH2—）、羧基与其相邻的亚甲基（—CH2COOH）。利用PA66盐-水的固液平衡实验数据以及PA66盐的熔点和熔化焓，回归得到UNIFAC模型的基团交互作用参数。基于构建的UNIFAC物性模型预测了0～100℃范围内PA66盐在水中的溶解度，与实验数据的平均相对误差为2.1%；采用该模型进一步计算工业操作条件（120℃）下的盐浓度，与Aspen自带参数的UNIFAC模型比较，其误差从20%左右降到5%以下。

关键词：尼龙66盐；水溶液；溶解度；UNIFAC模型；UNIFAC基团

2015-08-03收到初稿，2015-12-09收到修改稿。

联系人：冯连芳。第一作者：顾雪萍（1972—），女，博士，副研究员。

Received date: 2015-08-03.

引　言

尼龙66（PA66）以其优越的性能而被广泛应用于电子、汽车、纺织等领域，世界PA66的产能集中在欧美国家，国内产能最大的河南平顶山神马集团仅为20万～30万吨，单线产能低，远远不能满足需求[1]。对PA66聚合过程建立模型，消化吸收和改造所引进的工艺和装置是提升产能的有效办法。

根据PA66生产工艺流程，PA66盐溶液在浓缩槽中升温浓缩，若温度过低，溶解盐以固体盐形式析出，若温度过高，盐溶液开始聚合；在高温高压聚合过程中，随着温度的升高和反应时间的延长，系统中的水和PA66盐的含量均下降，PA66盐在水中的溶解度决定了体系中水的脱除速率。反应体系中存在溶解盐、二聚体、己二酸、产物PA66、低聚物、小分子水、CO2和NH3、易挥发物己二胺等组分。因此针对PA66聚合过程确定合适的溶解度计算模型及准确的模型参数尤为重要。

对组分的基团进行划分，定义新基团并回归参数，得到准确的尼龙66盐在水中的溶解度，为实现尼龙66生产过程的工艺优化提供指导。

1　物性计算方法选择和参数确定

热力学性质计算模型有两类，一是活度系数模型，二是状态方程模型。前者不考虑液体的可压缩性，适用于极性较强的体系；后者适用于非极性分子，可压缩流体[2]。而逐步聚合体系的单体大都是极性类物质，故对于PA66聚合体系选择活度系数模型比较合适。

活度系数模型采用活度系数修正了假设理想溶液状态下的Raoult定律，Schaffer等[3]采用Flory-Huggins（FH）模型仅计算了尼龙熔融缩聚过程中水的活度系数，目前不能准确知道PA66体系聚合物-溶剂交互作用参数，该模型不适用。Chen[4]将NRTL模型[5]和FH模型组合起来应用于聚合物体系，提出了Poly-NRTL模型，模型涉及多个二元交互作用参数；Seavey等[6]采用此模型提出了适用于水/己内酰胺/PA6混合物的相平衡模型，该模型适用的温度和组成范围较宽，可利用原有的NRTL模型数据库，但是其二元交互作用参数通常由平衡数据回归或者预测模型得到，其应用有一定的局限性。UNIFAC模型由Fredenslund等[7]提出，对于PA66聚合体系，由于文献相平衡数据的缺乏，且系统中存在多个组分，实验测定存在困难，采用数据回归关联系数的模型受到很大限制，而基于基团贡献法的UNIFAC物性模型具有预测功能，处理复杂体系更具优势。UNIFAC模型应用广泛[8-11]，选择UNIFAC物性模型计算物性和组分相平衡。

UNIFAC模型提出活度系数作为多组分组成和温度的函数方程，分为两部分表示。

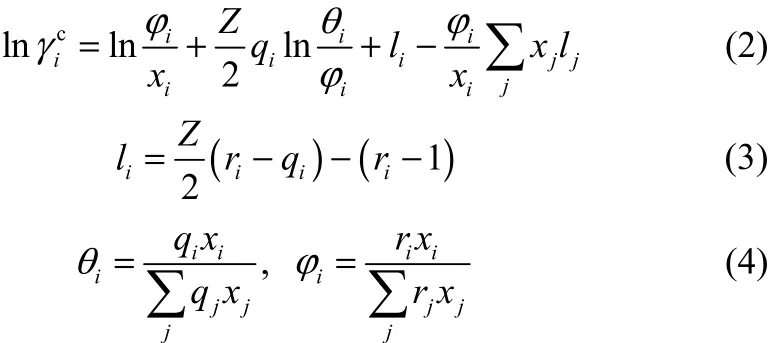
式中，Z为配位数。对于液体，Z = 10；纯组分的参数ri和qi由基团的体积参数Rk和表面积参数Qk求得，而Rk和Qk由Bondi[12]给出的基团体积Vwk和表面积Awk计算得到。

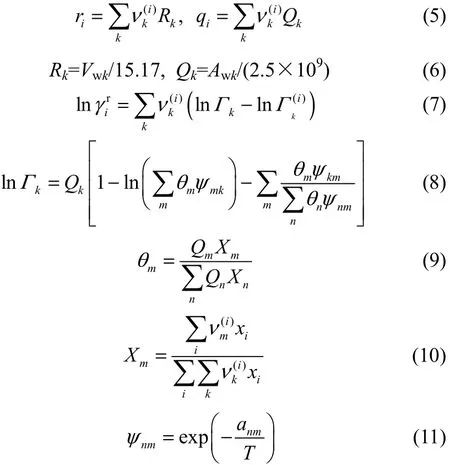
式中，anm和amn为基团交互作用参数，anm≠amn，必须由相平衡的实验数据求得，单位为K；T为体系的温度，单位为K。

基团体积参数Rk和表面积参数Qk是UNIFAC物性模型的重要参数，与基团本身的大小和尺寸有关，其值取决于基团的划分和参数值计算方法的可靠性。基团划分时基团应尽可能小，但是划分的基团又必须能够影响分子的性质。Lohmann等[11]、孙晓波[13]和曾思[14]针对研究体系组分定义新的基团，修正后UNIFAC模型预测数据的相对误差较小，预测结果较好。与以上经验式的基团划分不同，Wu 等[15]尝试采用量子力学分子轨道计算软件对分子中基团和原子的电荷进行检测，根据所划分的基团呈电中性和每个基团是最小单元的原则，从理论上给出了基团划分的准则。Gong等[8]和Lü等[10]认为新划分基团的Rk和Qk结构参数具有加和性，并且相似基团的结构参数相同，根据此假设可以由Bondi法[12]计算得到新定义基团的Rk和Qk；赵亚军等[16]提出一种基于元素和化学键的快速计算分子体积和表面积的方法，将构成分子的元素和化学键作为贡献单元，所计算分子体积和表面积参数的平均相对误差分别为2.02%、2.84%，该方法简单快速，应用范围更广。基团的划分和准确合理的计算方法是获得可靠的基团体积参数和表面积参数值的关键。

anm为UNIFAC物性模型的基团交互作用参数，由相平衡的实验数据得到，其值取决于实验数据是否可靠[17]。根据相平衡原理，忽略压力和热容差的影响，并用熔点和熔化焓代替三相点温度及其焓变后，可得到溶质的溶解度方程[7]。

由式(12)可知，根据相平衡数据，只要有组分i的摩尔分数xi，结合纯组分i的熔点及熔化焓，就可以计算活度系数γi，利用UNIFAC活度系数方程式(1)就可以回归得到基团交互作用参数。

2　基础数据的测定

2.1PA66盐的溶解度测定

2.1.1实验仪器及原料溶解釜，自制50 ml；CH1015型超级恒温水浴槽；85-1型恒温磁力搅拌器；精密温度计，量程为0～50、50～100℃，精度为±0.05℃；AL204型电子天平，精度为±0.1 mg。实验所用的原料PA66盐为BASF公司提供产品，室温下存放于干燥器中；己二酸和己二胺皆为市售，纯度为分析纯以上；水为实验室自制去离子二次蒸馏水。

2.1.2实验装置及实验步骤动态法测定溶解度的实验装置如图1所示，溶解釜由玻璃制成，夹套中通循环水，由超级恒温水浴控制其温度，体系温度由插入物料中的精密温度计测定。溶解釜中的耐腐蚀磁力搅拌转子连续搅拌以促进溶解并使固液两相快速达到平衡，并且外接冷凝管以防止溶剂的挥发。

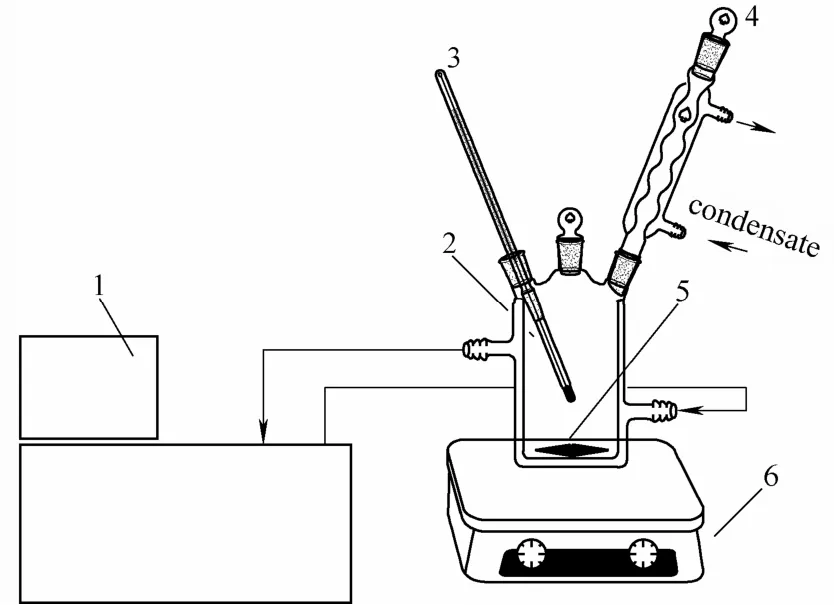
图1　PA66盐溶解度测定实验装置Fig.1　Solubility measurement apparatus of PA66-salt 1—thermostatic bath; 2—dissolution vessel; 3—thermometer; 4—condenser tube; 5—magnetic stirrer sub; 6—magnetic stirrer

用电子天平准确称量一定量的溶质和一定量的去离子水加入到溶解釜中；依次开启冷却水、恒温磁力搅拌器、超级恒温水浴开关，充分搅拌固液两相体系；控制超级恒温水浴的升温速率，用精密温度计测定溶解釜中的温度；当体系由浑浊变为澄清时，即为该溶质的溶解温度。

2.1.3实验方法和装置的可靠性验证为验证实验方法和装置测定数据的可靠性，如图2所示，测定己二酸在水中的溶解度，并与文献值[18]比较。由图2可见，在实验温度范围内，测定值与文献值吻合，该实验方法和装置测得的溶解度数据可靠。

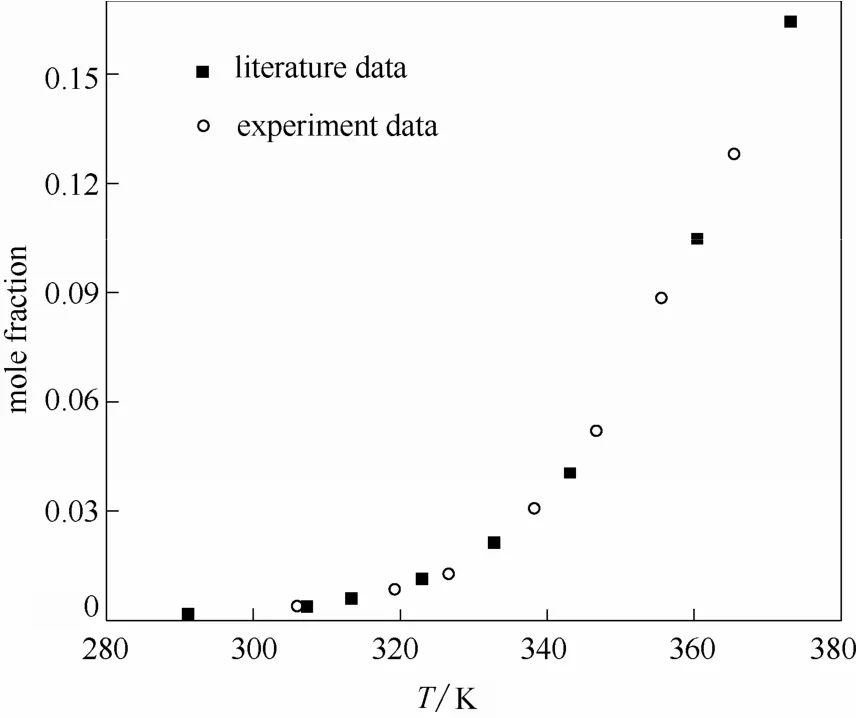
图2　己二酸在水中的溶解度实验值与文献值的比较Fig.2　Experimental solubility of adipic acid in water compared with data in literature

2.1.4PA66盐在水中的溶解度数据测定的PA66盐在水中的溶解度数据见表1，其中x为溶质的溶解度，以摩尔分数表示。

表1　PA66盐在水中的溶解度实验测定值Table 1　Solubility of PA66-salt in water

2.2PA66盐的熔点和熔化焓测定

文献[19-20]给出PA66盐的熔点为195℃±5℃，而其熔化焓数据并没有相关文献报道。采用DSC测定PA66盐的熔点和熔化焓，为UNIFAC模型参数回归提供基础数据。

取一定量的PA66盐置于真空烘箱中干燥12 h冷却后，用精度为0.01 mg的分析天平准确称取2～3 mg的样品制样，在PE-DSC7型差示扫描量热仪中以5℃·min−1的升温速率从100℃升温到350℃，其结果如图3所示。

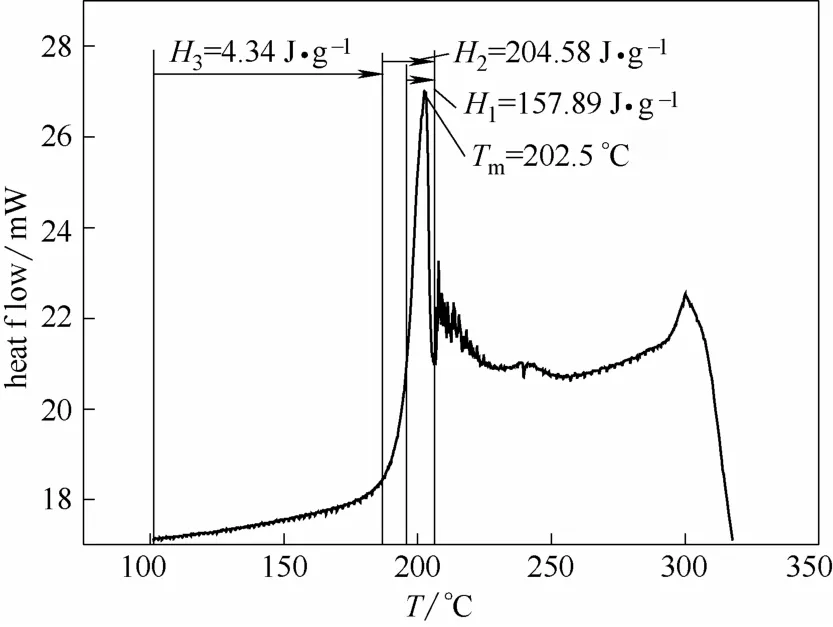
图3　PA66盐的热流曲线Fig.3　Heat flux curve of PA66-salt sample

当温度升至207℃时，PA66盐开始聚合，不能得到完整的PA66盐DSC熔化热曲线。将PA66 盐DSC熔化热曲线近似看成是对称的，采用如图3所示方法，先积分195.8～206.1℃温度区间，得熔化热H1=157.89 J·g−1；再积分186.9～206.1℃温度区间，得熔化热H2=204.58 J·g−1；最后积分100.9～186.9℃温度区间，得熔化热H3=4.34 J·g−1。采用以上假设，PA66盐的熔化焓H=H1+ 2(H3+H2−H1)= 259.97 J·g−1，摩尔质量MPA66-salt= 262.35 g·mol−1，转化为摩尔熔化焓ΔHMfus= HMPA66-salt=68200.0 J·mol−1。PA66盐的熔点TM=202.5℃=475.6 K。

3　UNIFAC模型及参数确定

3.1基团的划分和定义

反应体系中组分基团的划分是否合理是UNIFAC模型估算物性准确性的关键，需根据聚合体系中组分的结构进行基团的合理划分。涉及的化合物和官能团及其结构式列于表2。

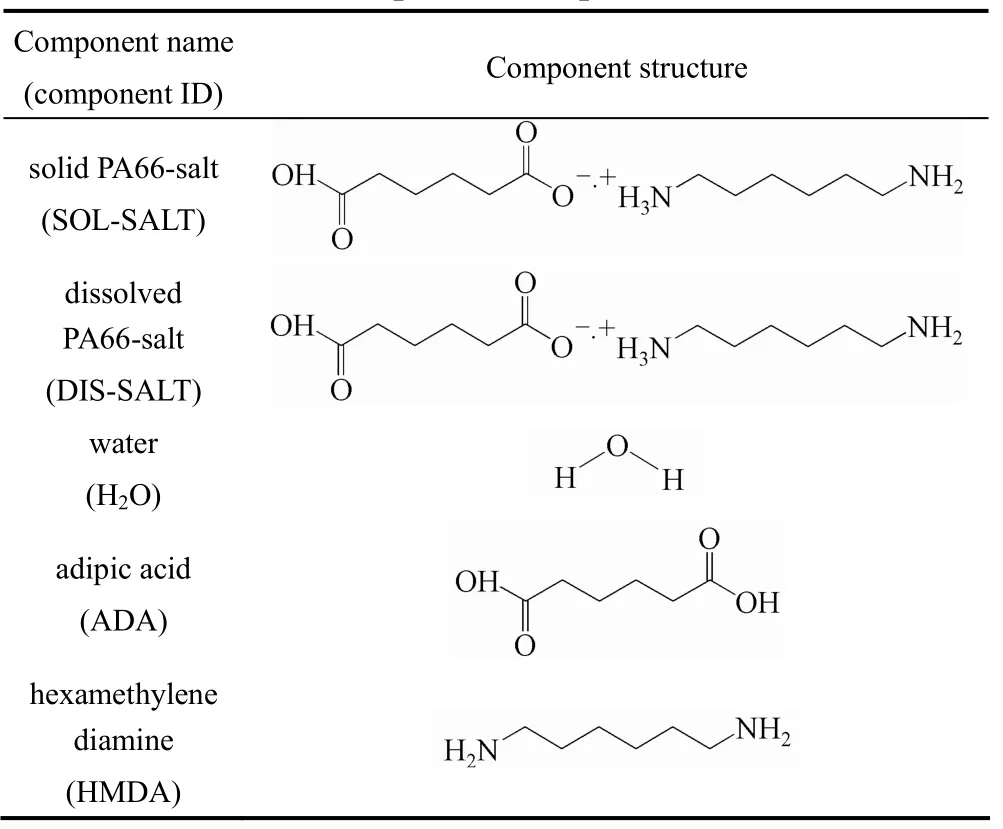
表2　PA66聚合过程中所涉及的化合物及其官能团Table 2　Components and function groups involved in PA66 production process

现有的基团不能准确定义PA66盐的结构。将羧基和氨基形成的缔合基团（—CH2COO−·+H3NCH2－）、羧基与其相邻的亚甲基（—CH2COOH）分别定义为新的UNIFAC基团。

UNIFAC模型中已存在羧基（—COOH）和酰胺键基团（—CONHCH2—），考虑到羧基对相邻亚甲基的影响，需要重新定义新的基团—CH2COOH；而新定义的羧基和氨基形成的缔合基团（—CH2COO−·+H3NCH2—）则为SOL-SALT 和DIS-SALT的特征基团。

3.2表面积参数和体积参数的计算

体系中涉及的常规组分含有的基团数目，及所划分基团的体积参数和表面积参数见表3。

新定义基团的体积参数Rk和面积参数Qk值可由结构参数具有加和性的性质近似计算。

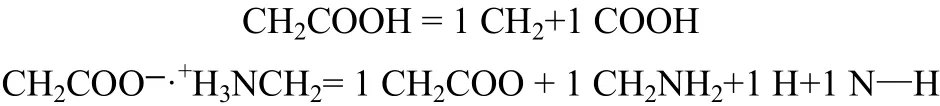
以上涉及的基团、元素和化学键的体积参数和表面积参数值采用Bondi法[12]及元素和化学键法[16]中的文献值计算。

3.3基团交互作用参数的回归

UNIFAC模型参数回归可以在Aspen软件的Regression模块中完成，输入的PA66盐溶解平衡方程式如下

参数回归过程中需要定义体系中所需要的基团结构和组分基团数目，以及PA66盐-水固液相平衡数据和PA66盐的熔点和熔化焓数据，回归得到基团交互作用参数。

基团参数Qk和Rk来自Aspen plus数据库和自定义计算值，以及组分基团的划分见表3；二元体系PA66盐-水固液相平衡数据采用本实验所测数据，见表1，其温度范围为305.45～363.05 K。在PA66盐物性估算的基础上回归基团交互作用参数aij值，见表4。

表3　组分基团的划分及其体积参数和表面积参数Table 3　Group identifications of components and group volume and area parameters

表4　UNIFAC模型的基团交互作用参数Table 4　Binary interaction parameters for UNIFAC model

4　模型验证

4.1PA66盐在水中的溶解度计算

为验证模型及参数的准确性，对0～100℃范围内PA66盐在水中的溶解度进行模拟计算，并与实验值进行比较，结果见表5，其平均相对误差AADP 为2.1%。其中，AADP表示相对误差百分数。

表5　PA66盐-水溶解度模拟值与实验值比较Table 5　Comparison of simulation data and experiment data of solubility of PA66-salt and H2O

4.2浓缩槽内盐浓度的模拟

由PA66的聚合工艺过程知，PA66聚合过程涉及汽液平衡。为了验证由PA66盐-水固液平衡数据回归参数后的UNIFAC模型能否应用于PA66聚合体系，考虑到盐浓缩过程涉及PA66盐-水的汽液平衡，模拟不同工业操作条件下的盐浓度，并与工厂数据对比，其结果见表6。

表6　工业操作条件下盐浓度计算值与测量值的比较Table 6　Comparison between calculation data and measurement data of salt concentration under industrial conditions

表6中，第2列为工厂浓缩槽出口盐浓度数据；第3列为将PA66盐重新划分基团，由固液平衡数据回归参数后UNIFAC物性模型的模拟结果；第5列为未考虑PA66盐的离子络合结构，采用数据库中的基团和参数的模拟结果。采用Aspen中默认基团的UNIFAC模型计算结果误差为20%左右，而采用划分新基团回归参数后的UNIFAC模型，计算结果相对误差大大降低，其值小于5%。

5　结　论

PA66聚合体系为极性体系，选择活度系数模型；由于文献相平衡数据的缺乏，且系统中存在多个组分，实验测定困难，基于基团贡献法的UNIFAC物性模型具有预测功能，其更具吸引力，选择UNIFAC活度系数模型计算物性和尼龙66盐的溶解度。

UNIFAC模型中包含基团体积参数、表面积参数和基团交互作用参数3个参数。基团体积参数和表面积参数值与分子大小和形状有关，其值取决于基团的划分；基团交互作用参数由相平衡数据回归得到。

实验测定回归参数所需的PA66盐-水的固液平衡数据和PA66盐的熔点及熔化焓；对体系组分进行基团划分，定义的新基团为羧基和氨基形成的缔合基团（—CH2COO−·+H3NCH2—）、羧基与其相邻的亚甲基（—CH2COOH），计算新定义基团的体积参数和表面积参数；回归UNIFAC模型的基团交互作用参数。

用回归参数后的UNIFAC物性模型模拟0～100℃范围内PA66盐-水的固液平衡溶解度，与实验值的平均相对误差为2.1%；采用该模型进一步计算了工业操作条件下的盐浓度，其相对误差为5%以下。

符号说明

AADP ——相对误差百分数

a ——基团交互作用参数，K

H ——熔化焓或熔化热，J·g−1

ΔH ——摩尔熔化焓，J·mol−1

M ——摩尔质量，g·mol−1

Qk——基团的面积参数

q ——纯组分的面积参数

R ——气体常数，8.314 J·mol−1·K−1

Rk——基团的体积参数

r ——纯组分的体积参数

T ——热力学温度，K

X——液相中基团的摩尔分数

x——液相中组分的摩尔分数

Z——配位数，对液体取为10

α——液相中组分的活度

Г——基团的剩余活度系数

γ——液相中组分的活度系数

θ——组分的面积分数

ν——基团数目

φ——组分的体积参数

上角标

c——结合项

exp——实验

fus——熔化

(i)——组分i

r——剩余项

sim——模拟

下角标

i, j——组分

k, m, n——组分的基团

M——熔点

1,2,3——分别为195.8～206.1℃、186.9～

206.1℃、100.9～186.9℃区间

References

[1] 华阳, 刘振明, 刘权毅, 等. 尼龙66国内外生产现状及发展建议[J]. 弹性体, 2010, 20(6): 78-82. HUA Y , LIU Z M, LIU Q Y, et al. Present situation and development suggestion of nylon-66 [J]. China Elastomerics, 2010, 20(6): 78-82.

[2] 顾凯, 黄继红. 聚合过程模拟与优化——基于Polymer Plus[M].北京: 化学工业出版社, 2010: 125. GU K, HUANG J H . Simulation and Optimization of Polymerization Process－Based on Polymer Plus [M]. Beijing: Chemical Industry Press, 2010: 125.

[3] SCHAFFER M A, MCAULEY K B, CUNNINGHAM M F, et al. Experimental study and modeling of nylon polycondensation in the melt phase [J]. Industrial & Engineering Chemistry Research, 2003, 42(13): 2946-2959.

[4] CHEN C C. A segment-based local composition model for the Gibbs energy of polymer solutions [J]. Fluid Phase Equilibria, 1993, 83: 301-312.

[5] RENON H, PRAUSNITZ J M. Local compositions in thermodynamic excess functions for liquid mixtures [J]. AIChE Journal, 1968, 14(1): 135-144.

[6] SEAVEY K C, KHARE N P, LIU Y, et al. A new phase-equilibrium model for simulating industrial nylon-6 production trains [J]. Industrial & Engineering Chemistry Research, 2003, 42(17): 3900-3913.

[7] FREDENSLUND A, JONES R L, PRAUSNITZ J M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures [J]. AIChE Journal, 1975, 21(6): 1086-1099.

[8] GONG X, LÜ Y, ZHANG Y, et al. Liquid-liquid equilibria of the quaternary system water + caprolactam + 1-octanol + ammoniumsulfate [J]. Journal of Chemical & Engineering Data, 2007, 52(3): 851-855.

[9] GMEHLING J G, ANDERSON T F, PRAUSNITZ J M. Solid-liquid equilibria using UNIFAC [J]. Industrial & Engineering Chemistry Fundamentals, 1978, 17(4): 269-273.

[10] LÜ Y C, LIN Q, LUO G S, et al. Solubility of berberine chloride in various solvents [J]. Journal of Chemical & Engineering Data, 2006, 51(2): 642-644.

[11] LOHMANN J, RÖPKE T, GMEHLING J. Solid-liquid equilibria of several binary systems with organic compounds [J]. Journal of Chemical & Engineering Data, 1998, 43(5): 856-860.

[12] BONDI A. van der Waals volumes and radii [J]. The Journal of Physical Chemistry, 1964, 68(3): 441-451.

[13] 孙晓波. 混合二元酸综合利用工程基础研究[D]. 郑州: 郑州大学, 2007. SUN X B. Study on engineering foundation of comprehensive utilization of mixed dibisic acids [D]. Zhengzhou: Zhengzhou University, 2007.

[14] 曾思. 工业聚酯装置酯化过程的建模与流程模拟[D]. 杭州: 浙江大学, 2010. ZENG S. Modeling and simulation of esterification section in industrial poly(ethylene terephthalate) process [D]. Hangzhou: Zhejiang University, 2010.

[15] WU H S, SANDLER S I. Use of ab initio quantum mechanics calculations in group contribution methods (Ⅰ): Theory and the basis for group identifications [J]. Industrial & Engineering Chemistry Research, 1991, 30(5): 881-889.

[16] 赵亚军, 司继林, 夏力, 等. 基于元素和化学键的快速计算分子体积和表面积的方法 [J]. 计算机与应用化学, 2013, 30(7): 739-742. ZHAO Y J, SI J L , XIA L, et al. A new method based on elements and chemical bonds for fast calculation of moleculer volume and surface [J]. Computers and Applied Chemistry, 2013, 30(7): 739-742.

[17] 陈明鸣. 对苯二甲酸生产中相关相平衡的测定与研究[D]. 天津:天津大学, 2003. CHEN M M. Determination and study on the corresponding phase equilibria in terephthalic acid manufacture [D]. Tianjin: Tianjin University, 2003.

[18] STEPHEN H, STEPHEN T. Solubilities of Inorganic and Organic Compounds [M]. Oxford: Pergamon Press, 1963.

[19] 张朝晖. 国内外尼龙66盐市场分析及需求预测[J]. 化工技术经济, 2002, 20(4): 26-28. ZHANG Z H. Market analysis and forecast of nylon66 salt [J]. Chemical Techno-Economics, 2002, 20(4): 26-28.

[20] 己二酸、己二胺、尼龙66盐[J]. 合成纤维工业, 1983, (3): 60-63. Adipic acid, hexamethylene diamine and PA66-salt [J]. China Syntehtic Fiber Industry, 1983, (3): 60-63.

DOI：10.11949/j.issn.0438-1157.20151235

中图分类号：TQ 028.8

文献标志码：A

文章编号：0438—1157（2016）02—0435—07

Corresponding author:Prof. FENG Lianfang, fenglf@zju.edu.cn

Thermodynamic modeling with new UNIFAC groups for solubility of nylon66-salt in water system

GU Xueping, TIAN Lulu, FENG Lianfang, ZHANG Cailiang
(State Key Laboratory of Chemical Engineering, College of Chemical Engineering and Biological Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)

Abstract:Modeling of PA66 polymerization process requires accurate solubility computation of nylon66-salt in water system. The UNIFAC activity coefficient method with new groups was applied to predict the solubility. The new groups were —CH2COO−·+H3NCH2— and —CH2COOH, which characterized the component’s special structure. The pure parameters of new UNIFAC groups and interaction parameters between new groups were obtained by regression with melting point and molar fusion enthalpy of PA66-salt as well as the solubility data of PA66-salt in water obtained by experiments. The UNIFAC model with new groups was used to simulate the solubility of PA66-salt in aqueous solution, giving a relative error of 2.1% from the experimental data. The model was further employed to simulate the concentration of PA66-salt under the industrial conditions (120℃) and gave a relative error as low as 5%, compared with 20% from the UNIFAC model with default groups in Aspen.

Key words:nylon66-salt; aqueous solution; solubility; UNIFAC model; UNIFAC groups