课堂教学中如何落实课程标准要求

敖大山（内蒙古兴安盟教研室，内蒙古 兴安盟 137400）



课堂教学中如何落实课程标准要求

敖大山
（内蒙古兴安盟教研室，内蒙古 兴安盟 137400）

摘 要：以听课者的角度解读人教版教材必修1、第一章1.3.2函数的奇偶性的几个要点。例谈用课标引领课堂教学的方向，落实课标要求是教师要努力实现的重要任务。

关键词：课程标准；高中数学；课堂教学

2015年9月17-18日，兴安盟高中数学教学基本功大赛在兴安盟所在地乌兰浩特市举行，全盟六个旗县市选出教学骨干共计12人参加了比赛。比赛采用的方法主要是展示一节完整的规范课；讲课内容均为《人教版必修一的1.3.2：函数的奇偶性》；比赛采用同课异构的形式进行选拔。

教师讲课过程中零散地表现出新课程改革要求的主体思想：就是以学生为主体的课堂。但比赛过程中很少看见，教师真正把本节课的《课标要求》落实到位，或者只是简单地讲解了函数的奇偶性，或者过分要求函数的奇偶性，试题难度过大。

下面以听课者的角度解读本堂课的几个要点。

内容：人教版教材必修1、第一章1.3.2函数的奇偶性

课标要求：1.结合具体函数了解函数奇偶性的含义。2.学会运用函数图像理解和研究函数的性质。

再看教材结构及要求：教材要求，观察图1.3-7，思考并讨论以下问题：

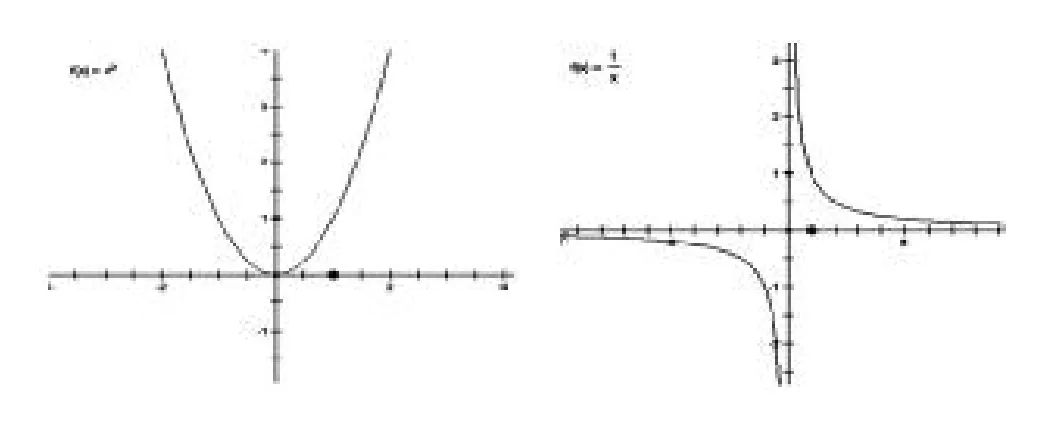
（1）这两个函数图像有什么共同特征吗？

（2）相应的两个函数值对应表是如何体现这些特征呢？

x -3 -2 -1 0 1 2 3 f（x）=x29 4 1 1 1 4 9

x -3 -2 -1 0 1 2 3 f（x）= x 3 2 1 0 1 2 3

这是教材给出的新课导入部分。

很多教师没有真正解读教材编写者的意图，引入新课五花八门，下面举例说明。

例1：直接给出函数f（x）=x2与f（x）= |x|，要求学生画函数图像，得出图像关于y轴对称的函数为偶函数。没有给出函数定义，直接用图像是否关于y轴对称来判断偶函数。显然没有理解教材编写的意图，片面地理解教材，给出了错误信息。

例2：观察函数图形，直接给出偶函数的定义。没有多余的讲解，然后用定义来判断函数的奇偶性。

教师只有认真研究课程标准、研究教材、研究学生、研究自己，课堂上才能不出现以上情况。那么课堂教学应该体现在哪几个方面呢？

一、教师引领

引领学生观察图像，发现什么？有什么特征？学生第一个反应就是：图像关于y轴对称。在这个基础上继续引领，如何利用解析式描述函数图像的特征呢？从函数值对应表可以看到，当自变量x取一对相反数时相应的函数值相同。

二、师生互动，教师引导

上面求值结果有何规律，是否f（1）与f（-1），f（2）与f（-2），f（3）与f（-3），…都有类似规律？让学生讨论并能否归纳总结出f（-x），f（x）的值是否相等。提出问题：因为x在定义域内的任意数，那么-x是否也满足在函数的定义域内呢？学生很容易发现：-x必须满足定义域内的条件。这样很容易得出偶函数的首要条件：偶函数定义域关于原点对称。（培养学生归纳总结的数学思想）

三、提出问题，巩固新知

1.f（x）=x2，x∈［-1，2］是偶函数吗？偶函数的定义域有什么特征？2.给出教科书34页例题。

四、探究奇函数的概念及特征

五、提出问题、巩固新知

（1）f（x）=x2，x∈［-1，2］奇函数的定义域有什么特征？

（2）给出教科书35页例题，巩固新知。

六、知识拓展

提出问题：从函数的奇偶性角度出发，可以将函数分成四类，即奇函数、偶函数、非奇非偶函数、即奇又偶函数。其中非奇非偶函数很容易理解，即函数的定义域不对称就是判断出非奇非偶函数，那么什么样的函数既是函数又是偶函数呢？（这个问题让学生去思考，培养学生数形结合的思想的好机会）。因为学生首先思考的切入点就是即关于原点对称又关于y轴对称同时满足的函数。

举例：f（x）=0，定义域为R。（即是奇函数又是偶函数）

七、合作探究

例题：判断下列函数的奇偶性。

（1）f（x）=x4（2）f（x）=x5（3）f（x）=x+

八、课堂小结

1.函数奇偶性的概念。2.判断函数的奇偶性。3.思想：数形结合的思想，归纳总结，特殊与一般的思想，类比推理等。

“函数奇偶性”是一个重要的数学概念，其研究必须经历从直观到抽象，从图形语言到符号语言，整节课学生通过自主探究活动来体验数学概念的形成，学习数学思考的基本方法，培养学生的数学思维能力。让学生掌握利用定义进行判断奇偶性的基本方法，理解定义域的要求，理解图像的对称性，了解奇偶性的四种类型，并初步运用奇偶性。

以上是通过开展一次活动，教师在课堂教学中课程标准落实不到位所想到的一点思考，无论是教学设计还是实际的课堂教学，对基础知识、基本技能、基本方法的落实情况，归根结底就是真正落实课程标准要求，用课标引领我们课堂的教学方向，落实课标要求是我们努力实现的重要任务。

参考文献：

［1］孙卫红，陈朝东.中国数学课程标准对估算要求的变化探析［J］.数学教育学报，2013（10）.

［2］张有德.对义务教育数学课程标准（实验稿）的思考与修订建议［J］.数学教育学报，2005（11）.

［责任编辑 赵建荣］

How to Implement the Requirement of Curriculum Standard in Classroom Teaching

AO Da-shan
（Hinggan League Teaching and Research Office，Hinggan League Inner Mongolia，137400，China）

Abstract:This article mainly talks about the key points of parity of function in chapter 1 PEP edition. It is an important task for teachers to lead the direction of the classroom teaching with curriculum standard and implement the curriculum requirements.

key words:curriculum standard；high school mathematics；classroom teaching

中图分类号：G63

文献标识码：A

文章编号：1673-9132（2016）19-0075-02

DOI：10.16657/j.cnki.issn1673-9132.2016.19.047