一种基于BP神经网络算法和低通滤波的水资源评估预测数学模型建模方法

林 炯，余伟江，余伟浩

(1. 华南师范大学物理与电信工程学院 广东广州510006；2. 华南师范大学信息光电子科技学院 广东广州510006)

一种基于BP神经网络算法和低通滤波的水资源评估预测数学模型建模方法

林 炯1，余伟江1，余伟浩2

(1. 华南师范大学物理与电信工程学院 广东广州510006；2. 华南师范大学信息光电子科技学院 广东广州510006)

基于BP神经网络算法建立水资源评估数学模型。首先获得大量相关的评估指标，通过主成分分析法(PCA)剔除不重要指标。对于指标赋权，先用基于蒙特卡罗的层次分析法(AHP-MCA)初步给指标赋权，由于此法具有一定主观性，因此进一步采用BP神经网络算法对所赋权重进行训练调节，过程中需要一个标准比对物，最终得到符合实际情况的权重因子。在建立预测数学模型前，针对可能的突变输入数据，采用低通滤波器将突变高频数据过滤，增加模型适用性，最后通过灰色模型GM(1，1)建立预测模型。

数学模型 BP神经网络 权重 低通滤波 灰色模型

0 引 言

评估某因素时，定量分析常常能给出更多的信息，因而寻找建立量化分析的方法非常重要。以建立水资源评估预测数学模型为例，首先需要筛选出影响此因素的相关已量化主要指标，然后从中筛选出少量独立且携带原始指标信息的重要指标，最后对指标进行赋权。降维即筛选重要指标和如何确定指标权重是建立整个评估模型的难点。

1 评估数学模型的建立

1.1 建立模型

模型尝试构造水资源压力指数ℑ，以衡量地区提供水资源能力。设从联合国水资源短缺图中选取了α个国家，收集筛选水资源相关指标，通过神经网络调节权重，得到水资源压力指数。建立评估数学模型思路，如图1所示。

图1 评估数学模型的建立步骤Fig.1 Procedures of establishing an appraisal mathematical model

1.2 指标筛选

把水资源短缺评估系统划分为两个子系统：物理系统(PS)和社会经济系统(SES)，根据经验选取相关指标。这样选取的指标数往往过大，模型应用性低，需进一步通过主层分分析法剔除次要指标。

1.2.1 主层分分析(PCA)

主成分分析可从原始变量中导出少数几个互不相关的主成分，使它们尽可能多地保留原始变量信息。主成分分析的具体步骤如下：

构造指标数据矩阵X，矩阵元xij(i＝1，2，…，α；j＝1，2，…，p)代表第i个国家的第j个指标，指标归一值：

定义相关矩阵R，矩阵元rij(i＝1，2，…，α；j＝1，2，…，p)：

解R本征方程：

求得本征值jλ(i＝1，2，…，m)和本征矢ai= (ai1，ai2，…，aip)(i＝1，2，…，m)。

根据m个特征向量，可求得m个主成分为：

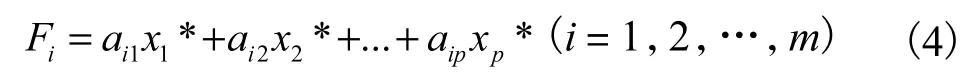
用m个较少的主成分代替p个主成分。

指标i的贡献率为：

若算得m个主成分中β个主成分的累计贡献

1.2.2 指标权重

1.2.2.1 基于蒙特卡罗的层次分析法(AHP-MCA)

蒙特卡罗方法可以解决在层次分析中判断矩阵阶数大于3的情形。运用此法给指标赋权重Wk，k＝1，2，…，β。具体步骤如图2所示。此法较主观，需进一步对权重进行调整。

图2 AHP-MCA算法流程图Fig.2 Flowchart of AHP-MCA

1.2.2.2 基于BP神经网络的方法

人工神经网络模型源于生物神经网络的启发，常用于估算依赖于大量输入数据的函数关系。假定联合国水资源短缺图中的信息是正确无误的，因此可作为神经网络算法训练过程中的一个标准比对。输入值为α个地区的各指标数值，输出值为各指标权重，水资源压力指数为：

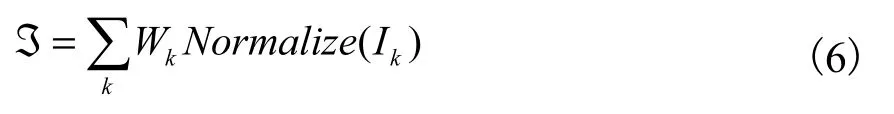
将每一次输出的水资源压力指数与联合国水资源短缺图标准(实际的WSI值)结果比较，若网络做出错误的判决，则通过网络学习，减少犯错误的可能。通过不断反馈和训练，使权重得到调节。具体步骤如图3所示。

图3 神经网络算法流程图Fig.3 Flowchart of Back Propagation(BP)Arithmetic

2 预测数学模型的建立

各指标可能因当地极端环境影响而出现突变数据，属高频噪声。可用低通滤波器使输出曲线光滑(见图4)，增加预测模型的适用性。

图4 低通滤波使输出图形变得“光滑”Fig.4 LPF makes output pattern “smooth”

2.1 低通滤波模型

2.1.1 Z变换和反Z变换

Z变换可以把任意离散信号f( n)从时域变换到频域：

频域显示更多突变数据细节，有利于对其进行处理。通过反Z变换可将信号变回时域：

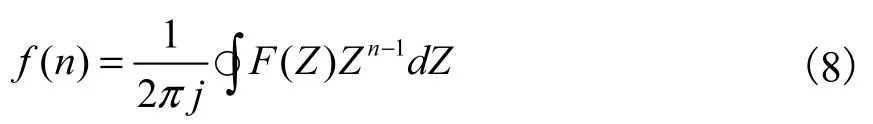
2.1.2 低通滤波变换到频域后，将突变数据进行低通滤波，保留低频部分

滤波流程如图5所示。

图5 低通滤波流程图Fig.5 LPF flowchart

2.2 灰色预测

灰色预测可用于寻找指标数据变化规律，通过构造微分方程来预测指标数据的变化规律。

设时间t1到t2某地水资源某指标数据：

求(1)

x灰色导数方程：

取平均值：

GM(1,1)灰色微分方程：

式中：a是发展系数，b是灰色作用量。

白化GM(1,1)得：

解得：

对结果做等间距取样得灰色模型：

累减(IAGO)得预测值：

2.3 预测模型有效性检验

计算：

3 结 论

评估数学模型主要讨论用神经网络对权重进行调整，尝试解决水资源短缺评估模型建立过程中的一个难点：如何确定合理的权重。建立预测模型前，采用滤波器过滤突变数据这一方法将会使模型更有实际应用性。在评估模型中，对筛选指标的讨论还有待深入研究。■

［1］ 刘彩红. BP神经网络学习算法的研究[D]. 重庆：重庆师范大学，2008.

［2］ 陈善广，鲍勇. BP神经网络学习算法研究[J]. 应用基础与工程科学学报，1995(4)：105-110.

［3］ 崔立志. 灰色预测技术及其应用研究[D]. 南京：南京航空航天大学，2010.

A Method Based on Back Propagation Arithmetic and Low-pass Filter to Build the Evaluation and Prediction Mathematical Model for Water Resources

LIN Jiong1，YU Weijiang1，YU Weihao2
(1．School of Physics and Communication Engineering，South China Normal University，Guangzhou 510006，Guangdong Province，China；2．School of Information and Optoelectronic Science and Engineering，South China Normal University，Guangzhou 510006，Guangdong Province，China)

To build an evaluation mathematical model for water resources，original evaluation indicators were selected，unimportant indicators by Principal Component Analysis(PCA)were eliminated and ultimately independent and important indicators were obtained，which actually carry all information of the original indicators．Then the Analytic Hierarchy Process based on Monte Carlo Algorithm(AHP-MCA)was used to preliminarily give weights．As this method is subjective，it is necessary to adjust the weights by Back Propagation Arithmetic(BP)．Ultimately，reasonable and real weights were obtained．Before building the prediction model，Low-pass Filter was used to filer abnormal data，which will add adaptability of the model．Finally，the prediction model was established by Grey Model GM(1,1).

mathematical model；Back Propagation Arithmetic；weight；low-pass filter；grey model

O29

A

1006-8945(2016)08-0029-04

2016-07-01