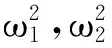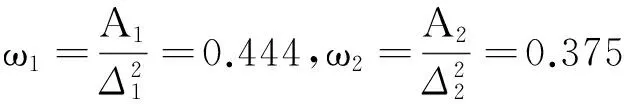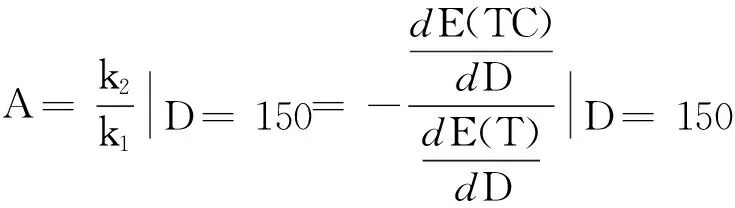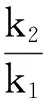考虑货主满意度的铁路货运超订分析

冯芬玲，刘海红，李菲菲,2

(1.中南大学 交通运输工程学院，湖南 长沙 410075;2.运城学院 经济管理系，山西 运城 044000)

考虑货主满意度的铁路货运超订分析

冯芬玲1，刘海红1，李菲菲1,2

(1.中南大学 交通运输工程学院，湖南 长沙 410075;2.运城学院 经济管理系，山西 运城 044000)

摘要:超订是收益管理的重要内容，在传统超订模型的基础上考虑货主的满意度因素，利用田口方法描述服务质量损失函数，建立了基于货主满意度的铁路货运超订模型，并对模型进行了算例分析。研究结果表明：在进行超定决策时，最优超订数量及成本目标函数的取值与超定成本和货主满意度的权重比值有关；货物的滞留概率越小，等待时间越短，超定成本越小。该模型同时考虑了铁路运输企业的超订成本和货主的满意度因素，对实施超订策略具有一定的指导意义。

关键词：超订；货主满意度；田口方法；质量损失

超订问题是收益管理的一个重要问题，目前关于超订的研究主要集中在航空客运业。Brumeiie等[1]提出了一个超订问题的静态模型，并且指出它是两级票价座位分配问题的一般模型的特例。Rothstein[2]将航空超订问题看做一个非均匀马尔科夫决策过程，并且采用动态规划的方法对模型进行了求解。Subramanian等[3]针对单航段多票价等级的航空座位分配提出了考虑超订的马尔科夫决策过程。Yoshinor[4]分析了超订策略对其他航班利润的影响，研究了超订模型的毛利润和净利润的关系问题。但是将超订问题应用于货运业，特别是铁路货运业的研究还不是很多。在航空货运业方面，考虑到航班运输能力的不确定性时。Kasilingam[5]提出了基于随机运输能力的航空货运超订的数学模型。Kasingam[6]分析了航空货运业的运作管理特征，提出了研究航空货运收益管理的超订模型。在集装箱运输方面，Ha[7]应用期望边际收益和曲线模型，对集装箱班轮公司的舱位控制策略进行了研究[9-10]。卜祥智[8]等建立了不考虑和考虑空箱调运的海运集装箱能力分配随机规划模型。段刚等[4-10]设计了铁路集装箱空箱调运问题的遗传算法，并将适箱货物按重要程度分为不同的优先等级，建立了铁路集装箱空箱调运非线性混合整数规划模型。王学峰等[11]利用仿真技术对集装箱船的超订问题进行了研究，结果表明大型集装箱船舶实施超订技术的效果明显。

上述研究在进行超订策略决策时，都没有考虑顾客的满意度影响，DavidArthur等[12]建立了几个超订模型，然后测试了不同超订策略对航空公司收益的影响，并通过顾客等待时间分布估计补偿成本，但是忽略了顾客满意对收益的影响。张国坤[13]以二项式分布描述顾客到达，建立了超订模型来计算最佳可信座位数。彭斯俊等[14]将收益最大化和乘客滞留率最小化相结合，建立了多目标规划的超售模型，并利用演化计算求得了模型的解。孙晓东等[15]基于顾客等待时间分布，建立了航空公司补偿成本，并进一步估计了航空公司拒绝顾客登机所必须承担的补偿成本，但是并没有考虑顾客的滞留率对航空公司的影响。

这些文献对研究铁路货运业的超订模型具有一定的参考价值，但是铁路货运业有自己的特点，并不完全等同于航空货运业和集装箱运输。在运输市场竞争日益激烈的今天，顾客满意度是企业提高市场份额的一个关键因素。但在采用超定策略时，若超订不当，会不可避免的带来部分货物无法按时准确的运输，导致货主抱怨，降低了货主满意度，从而给铁路运输企业形象、信誉方面带来不可挽回的损失，最终影响到铁路运输企业的经济收益。这种无形损失是铁路运输企业不得不承担的隐形成本，这种成本实质上是因为造成了产品(铁路运输服务)质量特性与标准有了偏差，而给铁路运输企业带来了质量损失。因此，只从超订成本角度考虑企业利益是片面的，应综合考虑超订成本和由于超订策略导致的货主满意度降低带来的损失。所以，本文拟在前人研究的基础上，根据铁路货运业自身的特性，在铁路货运市场中应用超订技术，并在传统超订模型的基础上考虑货主的满意度因素，以期实现铁路运输企业和货主的双赢。

1我国铁路货运引入超订技术的可行性分析

1.1我国铁路货运引入超订技术的必要性

货物运输合同签订后，承托双方都应该信守合同，严格履行。但是托运人或是收货人往往会由于特殊原因，对承运后的货物，向货物所在的中途站或到站提出变更到站，变更收货人，或者在发送前向发站提出取消托运，这样将会降低货物计划运输的质量，扰乱正常的运输秩序。特别是在运输旺季，很多货主可能会有货源由于超过铁路运输能力而无法装车，而铁路运输企业却因为有货主临时取消托运或者在装车日没有出现而产生闲置运力，造成资源浪费。基于效益最大化的理论，这无论是对其他的托运人还是铁路运输企业来说都是不合理的，因此，为了最大限度的增加铁路运输企业的效益，同时使得更多的托运人有机会获得运力提供，在铁路货运市场中引入超订技术是十分必要的。

1.2超订技术概述

在航空客运业中，所谓“超订”是指航空公司售出比该航班的最大载客量要多的机票。超订的目的是为了减少空位损失，优化收益。因为某些乘客没有在起飞时间赶到或者订了另外一个航班却没有取消原来的预订，空出的座位使航空公司遭受损失。另一方面，超订可能会导致持票者被拒绝登机，这时航空公司不但要承担赔偿责任，而且也要承受商誉方面的不良影响。因此航空公司必须谨慎处理，力求找出一个既能最有效利用空位，又能将拒登机造成的损失降低到最小的平衡点。通常大多数航空公司都会采取超订策略去平衡这两者的损失并且获得最大化的利润。

超订之所以在航空客运经营中被大量采用，是与航空客运产品的特性分不开的，很多别的行业同样也可以采用超订技术，经过分析我们不难发现适于使用超订技术的行业一般具有以下特征[16-17]：

1)能够提供的产品数量有限；2)产品具有易逝性；3)可以接受提前预定，并且允许取消预定；4)出现超订的情况时，并没有不可挽回的损失。

基于上述超订技术适应的行业，我们发现航空客货运输业、酒店业等都可以采用超订技术，还有些行业也具有使用超订技术的可能性。

1.3铁路货运实施超订技术可行性

我国铁路货物运输计划是根据国民经济各部门的生产计划、供应计划和销售计划进行编制的，会明确规定货物的运输数量和运量构成，所以对于铁路运输企业来说能够提供的运输能力是有限的。铁路运输企业允许货主提前申请请求车来满足需要的运力，若有运力空虚，在装车日一旦货物装车列车运行则未被利用运力的效益就会归为零。基于铁路货物运输的以上特点可以发现我国的铁路货运满足实施超订技术的特点，因此对我国的铁路货运实施超订技术具有一定的可行性。

运输开始前如果还有剩余运力未被利用，即列车货运量低于可得运力时就会有虚耗运力存在，这对于可变成本较低固定成本较高的铁路货运来说是一种资源浪费，称之为虚耗损失。如果运输开始时，到达站货物超过运力总量，那么货物有部分无法装车，铁路需要对此部分货物给予合理安排，并给货主一定的经济赔偿，这是超订赔偿所导致的损失。因此，在实施过程中的一个原则就是尽量使运力虚耗损失和超订赔偿的总成本最小化原则，也就是在虚耗损失成本和超订赔偿成本中寻求一种平衡。

2基于货主满意度的铁路货运超订模型的构建

2.1问题的提出

由于在面临超订决策时不仅要考虑经济上的损失，也会涉及到声誉方面的损失，因此铁路货运业在应用超订策略实现收益最大化的同时，还必须考虑到货主的满意度，只有实现货主满意才能吸引到新货主，以弥补货主流失。以货主满意为核心，以货主忠诚为目的来构建和实施服务满意战略，是铁路货运业谋求长远发展，实现收益最大化的必然选择与重要手段。因此，本文在建立超订模型时引入基于货物等待时间和货物滞留量的铁路货物运输服务质量损失函数来描述货主对其服务的满意度，并假定运输服务质量损失越小，货主对其满意度越高；运输服务质量损失越大，货主对其满意度越低。铁路货运部门应以货主为中心，找出一个既能减少虚耗损失，又能将其服务质量损失降到最低的平衡点。

2.2模型假设及符号说明

为简化模型，作出如下假设：

1)铁路货运企业对货物的到达时间有严格的管理要求，在无外界不可抗拒因素下尽量做到货物的准时到达；

2)货主申请请求车的需求是无限的；

3)超订过度造成货物无法装车，货运企业需要给予赔偿，预定车辆在货物装车成形前可以取消预定且货主不承担责任；

4)在超订过度时货物被拒绝装车的概率服从二项式分布。

本模型的主要参数、符号说明及变量定义如下：

P为申请请求车的货物到达率，0≤P≤1，f(P)为密度函数；C为货运企业可提供的运力；M为单位运力虚耗损失成本；N为单位运力超订赔偿成本；D为超订提供运力限制量。

2.3模型构建

2.3.1铁路运输企业超订成本最小化模型的构建

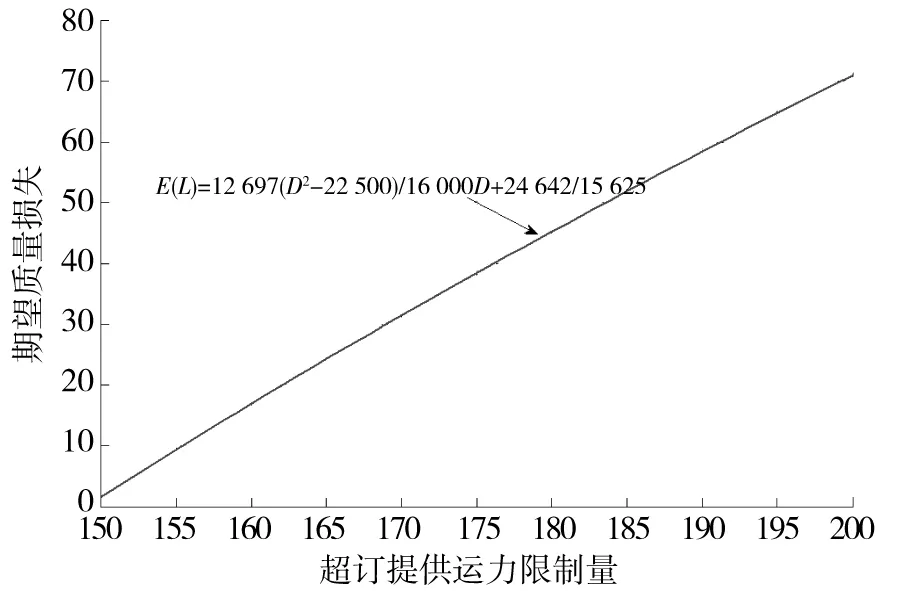
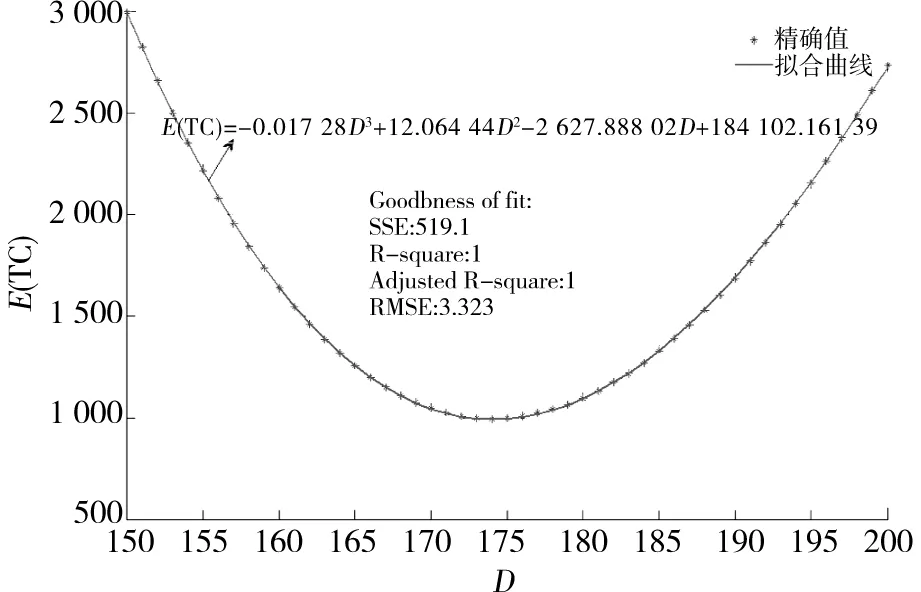
在进行铁路货运运力超订的过程中，一方面会由于超订不足造成运力虚耗，发生虚耗损失成本；另一方面又会由于超订过度造成部分货物被拒绝装车，发生超订赔偿成本，如何使得超订成本最小，实现超订收益最大化，是铁路运输企业首先要考虑的因素。

最优运力超订量的经济影响可以用如下决策树描述：

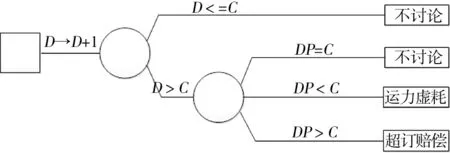
图1　最优超订运力决策树Fig.1 Optimal overbooking capacity decision tree

当PC/D时，铁路货运运力超订量为D·P-C。

而当超订水平增加时，往往会导致铁路运输企业商业信誉的下降，从而造成单位运力超订赔偿成本的增加。因此，超订赔偿成本应该是关于超订水平的一个单调不减的函数，这样更加符合实际情况，且单位运力超订赔偿成本应大于单位运力虚耗损失成本，即N>M。对于超订赔偿成本的函数形式，应根据铁路运输企业运营管理的历史数据的统计分析，并综合考虑超订行为可能对铁路运输企业的商业信誉所造成的不良影响来确定，本文假设超订赔偿成本函数如下所示：

(1)

其中a,b和c为正数，b≤1。在运输实务中，只有当C

运力虚耗损失期望成本

(2)

运力超订赔偿期望成本

(3)

(4)

s.t.

(5)

2.3.2基于货主满意度的服务质量损失最小化模型的构建

一般而言，铁路货物运输企业应安全、准确、快捷、经济、便利地运输货物来满足国民经济各部门的需要，并以此取得社会各界人士的信赖。研究质量损失比较常用的方法为田口方法，田口方法是日本管理学家田口玄一提出来的一种描述质量损失函数的方法，他认为，质量损失是由于质量特性偏离设计目标值造成的，有偏离就会有损失。而影响货主满意度的比较重要的因素为货物的滞留量和滞留货物在下批运输的等待时间。因此可以将这两个因素作为运输服务的质量特性。田口方法所建立的产品质量损失模型是以绝对质量偏移为基础，针对的是单一的质量指标。故本文采用田口方法并将其进行扩展来描述基于货主满意度的质量损失函数。

单一的质量损失函数如下所示：

(6)

(7)

设y=m时，L(y)=0,即L(m)=0，又因为L(y)在y=m时有极小值，所以L′(m)=0，二阶以上的高阶项影响很小，将其略去则可以得到一元质量损失函数为：

L(y)=K(y-m)2,其中K是不依赖于y的常数。

(其中，A,Δ分别表示不合格损失和容差)图2　一元质量损失函数Fig.2 Quality loss function of one variable

在本文中建立二元的质量损失函数，具体如下所示：

假设铁路运输企业在采用超订策略时的服务质量特性是一个关于货物等待时间t和货物滞留量q的二元函数，其分质量特性和t，q的目标值分别为m1,m2，则将其在m1,m2处进行泰勒展开可得：

(7)

(8)

(9)

其期望损失函数为：

式中：fft——钢纤维再生混凝土的轴心抗拉强度，N/mm2；ft——基准组(对照组)混凝土轴心抗拉强度，N/mm2；λf——钢纤维的含量特征值。

(10)

当|t-m1|≤Δ1且|q-m2|≤Δ2时，铁路货物运输服务质量合格；

当|t-m1|>Δ1或|q-m2|>Δ2时，铁路货物运输服务质量不合格。

当铁路货物运输服务质量不合格时，货主可以进行投诉要求其重新为其安排服务，铁路运输企业应引起高度重视，此时给铁路运输企业带来的损失分为3种情况：

在式中t为货物的等待时间，假定服从一般的指数分布，概率密度为f(t)=λe-λt，则E(t)=1/λ，D(t)=1/λ2，其中1/λ为货物的平均等待时间；q为货物的滞留量，当P>C/D时，一定数量的货物会被滞留。假定货物滞留量服从二项式分布，每单位的货物被滞留的概率为η，则服从(DP,η)，可知E(q)=DP·η，D(q)=DP·η(1-η)，为了保证货物被滞留的风险不会过高，需将滞留量限制在一定的范围内，即0≤E(q)≤Q。

(11)

2.3.3超订模型的构建

基于以上分析可以得到基于货主满意度最高条件下铁路货物运输收益最大化超订模型：

s.t.

(12)

s.t.

(13)

3算例分析

假定某铁路运输企业可以提供的运力C=150，其超订赔偿成本参数及虚耗损失成本如表所示：

表1　参数取值

在采用超订策略时其容差和不合格损失取值分别如表2所示。

表2　容差及不合格损失取值表

则可以据此计算其权重分别为：

货物的到达率服从[0.8,1]上的均匀分布，分布函数为：

(14)

密度函数为

(15)

另外，假设货物的平均等待时间设定为1/λ=2，货物的滞留率η=0.2，最大允许滞留量Q=30。

因为式(12)中的第二项的积分函数是不可积的，但是它的原函数是存在的，只是不能用初等函数表示而已。故采用数值积分中精度较高、收敛速度较快的Romberg积分法来求解。其积分公式如下所示：

(16)

其中外推加速公式可简化为：

m=1,2,…k=1,2,…

(17)

3.1最优超定数量及成本目标函数E(TC,L)值的确定

利用matlab工具，式12采用Romberg的积分计算结果如图所示：

图3　期望超订成本图示Fig.3 Diagram of expect overbooking cost function

由图3可以得出：当D=174时，可取得期望超订成本的最小值995.1。

式(11)的积分表达式为：

(18)

(19)

函数的图像如图4所示，该函数为单调递增函数。

图4　期望质量损失图示Fig.4 Diagram of expect quality loss function

从图4可以看出，当D=150时，可取得期望质量损失的最小值1.577 1。

当D=174时(超订成本最低点)，可求得期望质量损失值为37.041 1。可以看出，当超订成本取最小值时，期望质量损失值比较大，货主满意度并不高，会给铁路运输企业形象、信誉方面带来了不可挽回的损失。应在超订成本和质量损失两方面寻求一个平衡点，以期实现铁路企业和货主的双赢。因此，对E(TC)和E(L)采用如下系数加权法，得到加权后的成本目标函数：

E(TC,L)=k1E(TC)+k2E(L)

(20)

(21)

因E(TC)不存在解析表达式，这里对E(TC)的数值解采用数值拟合的方法来解析表达。拟合的结果如图5所示：

图5　数值拟合图Fig.5 Numerical fitting figure

E(TC)的拟合函数为：

E1(TC)=-0.017 28D3+12.064 47D2-

2 627.888 02D+184 102.161 39

(22)

残差平方和SSE=519.1，拟合系数R-square=1, 调整拟合系数AdjustedR-square=1,均方残差RMSE=3.323。这些数据说明拟合的精确度很高。则

(23)

(24)

图取不同值时函数图示Fig.6 Diagram of function when take different values

3.2不同条件下期望质量损失的变化

当λ和η分别取不同的值时，期望质量损失的表达式分别为

(25)

(26)

其图示分别如图7～8所示。

图7　λ取不同值时期望质量损失Fig.7 Diagram of expect quality loss function when λ take different values

图8　η取不同值时期望质量损失Fig.8 Diagram of expect quality loss function when η take different values

从图8可以看出，随着λ的增大，即货物平均等待时间的减小，期望质量损失减小，随着滞留率η的增大，期望质量损失增大，因此，应减少平均等待时间和滞留率才能使得期望质量损失降低。

4结论

1)为解决基于收益管理的铁路货运超订问题，在传统超订模型的基础上考虑了货主的满意度因素，构建了基于货主满意度的铁路货运超订模型；

2)通过算例对其进行数值仿真，说明了在进行超定决策时，最优超订数量及成本目标函数E(TC,L)的取值与超定成本和货主满意度的权重比值有关；

3)并进一步研究了货物在不同的滞留概率和等待时间条件下的超订成本，说明了货物的滞留概率越小，等待时间越短，超定成本越小。

参考文献：

[1]BrumeiieSL,McGiiiJI.Ageneraimodeiforairiineoverbookingandtwo-ciassrevenuemanagementwithdependentdemands[R].Vancouver:UniversityofBritishCoiumbia, 1989.

[2]RothsteinM,StoneAW.Passengerbookingleveis[C]//Noordwijk:Proceedingsofthe7thAGIFORSSymposium, 1967:7-8.

[3]SubramanianJ,StidhamS,LautenbacherCJ.Airiineyieidmanagementwithoverbooking,canceiiations,andno-shows[J].TransportationScience, 1999, 33(2):147-167.

[4]YoshinoriS.Thenetbenefit0fairlineoverbooking[J].TransportationResearchPartE, 2006, 42:1-19.

[5]KasilingamRG.Aneconomicmodelforaircargooverbookingunderstochasticcapacity[J].ComputersIndustryEngineering, 1997, 32(1):221-226.

[6]KasiiingamRG.Aircargorevenuemanagement:characteristicsandcompiexities[J].EuropeanJournaiofOperationaiResearch, 1996, 96(1):36-44.

[7]HaDW.Capacitymanagementinthecontainershippingindustry-theapplicationofyieldmanagementtechniques[D].Knoxville,UniversityofTennessee, 1994.

[8] 卜祥智，赵泉午，黄庆，等．考虑空箱调运的集装箱海运收益管理能力分配优化模型[J]．中国管理科学，2005，13(1)：71-75．

BUXiangzhi,ZHAOQuanw,HUANGQing,etal.Optimalcapacityallocationmodelofoceanshippingcontainerrevenuemanagementconsideringemptycontainertransportation[J].ChineseJournalofManagementScience, 2005, 13(1):71-75.

[9] 段刚, 张慧, 陈莉，等. 铁路集装箱空箱调运问题的遗传算法[J]. 铁道科学与工程学报, 2011, 8(3): 110-115.

DUANGang,ZHANGHui,CHENLi,etal.Geneticalgorithmforrailwayemptycontainerallocationproblem[J].JournalofRailwayScienceandEngineering, 2011, 8(3): 110-115.

[10] 段刚,陈莉,陈志忠，等.基于适箱货物优先级的铁路空箱调运模型 [J]. 铁道科学与工程学报, 2011, 8(4): 86-89.

DUANGang,CHENLi,CHENZhizhong,etal.Railwayemptycontainerallocationmodelbasedoncargorank[J].JournalofRailwayScienceandEngineering, 2011, 8(4): 86-89.

[11] 王学峰，张仁颐，殷明．箱位超订技术在集装箱船舶大型化下的应用[J]．上海交通大学学报，2007，41(2)：289-292.

WANGXuefeng，ZHANGRenyi，YINMing.Applicationofslotsoverbookinginenlargingofcontainerships[J].JournalofShanghaiJiaotongUniversity. 2007, 41(2):289-292.

[12]ArthurD，MaloneS，NirO．Optimaloverbooking[J]．TheJournalofUndergraduateMathematicsanditsApplications，2002, 25(3):283-300.

[13] 张国坤．机票超售建模和数值分析[J]．中国民航飞行学院学报，2001，12(1)：45-48．

ZHANGGuokun，Anairplaneover-bookingmodelandnumericalanalysis[J].JournalofChinaCivilAviationFlyingCollege, 2001, 12(1):45-48.

[14] 彭斯俊，万丽军，唐涛，等．基于演化计算的机票超售建模[J]．武汉理工大学学报(信息与管理工程版)，2002，24(5)：24-27．

PENGSijun,WANLijun,TANGTao,etal.Anairplaneover-bookingmodelbasedonthegeneticalgorithm[J].JournalofWuhanUniversityofTechnology(Information&ManagementEngineering), 2002, 24(5):24-27.

[15] 孙晓东，田澎，焦玥．基于等待时间和服务质量损失的机票超售策略[J]．工业工程与管理，2007，12(6)：100-104．

SUNXiaodong,TIANPeng,JIAOYue.Researchonoverbookingstrategybasedonpassengerwaitingtimeandservicequalityloss[J].IndustrialEngineeringandManagement, 2007, 12(6):100-104.

[16] 张丽，闫世锋．航空公司收益管理之超售策略研究[J]．行业管理，2006(9)：141-142．

ZHANGLi,YANShifeng,Researchonoverbookingstrategyofairlinerevenuemanagement[J].GroupEconomy, 2006(9):141-142.

[17] 顾建庄．航空客运的超售问题分析[J]．西南民族大学学报，2007，33(3)：580-584．

GUJianzhuang.Analysisoftheoverbookinginairpassengertransport[J].JournalofSouthwestUniversityforNationalitiesNaturalScienceEdition, 2007,33(3):580-584.

Overbooking analysis of railway frieght transportationbased on frieght owner satisfaction degree

FENG Fenling1, LIU Haihong1, LI Feifei1,2

(1.SchoolofTrafficandTransportationEngineering,CentralSouthUniversity,Changsha410075,China；2.DepartmentofEconomicsandManagement,YunchengUniversity,Yuncheng044000,China)

Abstract:Overbooking is an important part of the revenue management. On the basis of the traditional overbooking model, this paper considered the cargo owner satisfaction, and used the Taguchi method to describe the service quality loss. The overbooking model was constructed with cargo owner satisfaction. The results show that during the overdetermined decision making, the optimal overbooking quantity and the value of objective cost function are related to the ratio of the total cost and cargo owner satisfaction, and that the smaller the probability of the goods retention, the shorter of the waiting time, then the overdetermined cost is less. This model allows for the railway cargo transport overbooking cost and the cargo owner satisfaction, so it has much value to overbooking practice.Key words: overbooking; cargo owner satisfaction degree; Taguchi method; quality loss

收稿日期：2015-09-27

基金项目：中国铁路总公司科技研究开发计划课题(2015F024)

通讯作者：冯芬玲(1973-)，女，河北邯郸人，副教授，博士，从事交通运输规划与管理研究；E-mail:ffl0731@163.com

中图分类号：U2-9

文献标志码：A

文章编号：1672-7029(2016)05-0985-09