外倾式拱梁组合桥梁的稳定性研究

傅金龙，黄天立，夏智

(中南大学 土木工程学院，湖南 长沙 410075)

外倾式拱梁组合桥梁的稳定性研究

傅金龙，黄天立，夏智

(中南大学 土木工程学院，湖南 长沙 410075)

摘要:外倾式拱梁组合桥梁是一种新颖的桥梁形式，然而其外倾式拱肋的稳定性问题十分突出。以一座实桥为背景建立空间有限元模型，并以现有的拱桥稳定性分析理论为指导，对该桥在成桥状态下和吊杆张拉施工过程中的结构稳定性进行分析，通过对比分析得出：该桥的失稳模态主要表现为拱肋面外失稳；几何非线性和材料非线性对该桥的稳定性有显著影响；采用内、外吊杆交替张拉的方式可显著提高张拉过程中的结构稳定性；外吊杆对该桥的稳定性影响显著，采用空间多索面体系有利于提高该桥的稳定性。另外，通过大量计算揭示拱肋矢跨比、外倾角及截面刚度等参数对该桥稳定性的影响，并从中得到一些有益的结论，可供同类工程参考。

关键词：外倾式拱肋；稳定性分析；弹性屈曲；非线性；成桥状态；吊杆张拉过程；参数分析

外倾式拱梁组合桥梁又被称为蝴蝶拱桥[1]，是一种新颖的桥梁形式，其外观优美、造型别致，近年来多被用于城市景观桥梁的建设。该桥型的最为显著特点就是其外倾式拱肋，即两片拱肋横桥向的间距从拱脚处到拱顶处逐渐变大，通常两片拱肋之间不设置横向支撑，因而它们之间无法形成整体，然而单片拱肋的侧向抗弯刚度和抗扭刚度有限[2]，并且外倾式拱肋本身承受了较大的面外荷载，导致外倾式拱肋的横向稳定性[3-7]通常较差，容易发生面外失稳，因而有必要对外倾式拱梁组合桥梁的稳定性问题进行研究。本文以江西省南昌市艾溪湖大桥为研究对象，该桥为一座典型的外倾式拱梁组合桥梁，本文首先对该桥在成桥状态下的空间稳定性进行了分析，而后从吊杆张拉施工过程的结构稳定性的角度考虑，对不同的吊杆张拉方案进行了比选，最后对外倾式拱肋的矢跨比、外倾角以及截面刚度等参数与结构稳定性之间的关系进行了分析，并从中得出了一些有益的结论，可为同类工程的设计与施工提供参考。

1拱桥稳定性分析理论及相关规范要求

拱桥的稳定性问题可以分为2类[8]：第1类稳定问题和第2类稳定问题。第一类稳定问题的力学概念清晰明确，求解相对容易，而且在许多情况下其临界荷载可近似代表第2类稳定问题的临界荷载上限。但是，实际的拱桥结构不可避免地存在不同程度的初始弯曲、残余应力以及偏心等缺陷，因此拱桥在实际工程中的稳定问题通常都表现为第2类稳定问题。实际工程中的拱桥的失稳均发生于弹塑性变形阶段，这就需要考虑结构变形和材料弹塑性对结构稳定性的影响，按照几何非线性和材料非线性来求解拱桥的极限承载力。

1.1有限元分析理论

1.1.1第1类稳定问题的有限元分析理论

在结构发生失稳前，结构满足线性假设，处于初始构形线性平衡状态：

([K]0+[K]σ){Δu}={ΔP}

(1)

式中:[K]0为弹性刚度矩阵；[K]σ为几何刚度矩阵；{Δu}为位移向量；{ΔP}为荷载向量。

当结构处于临界状态时，即使{ΔP}→0，{Δu}也应有非零解，因此，可得：

|[K]0+[K]σ|=0

(2)

(3)

于是式(2)可写成：

(4)

式(4)就是第一类稳定问题的控制方程，这样就将稳定问题转化为数学上求解特征值的问题。求解方程得到的最小特征值λ即为荷载稳定安全系数，相应的特征向量即为失稳模态[9]。

1.1.2结构极限承载力(第2类稳定问题)有限元分析理论

从力学分析角度看，分析桥梁结构极限承载力的实质就是通过不断计入几何非线性和材料非线性对刚度矩阵的影响，求解平衡方程，寻找其极限荷载的过程。结构在不断增加的外荷载作用下，刚度不断发生变化，当外荷载产生的压应力或剪应力使得结构切线刚度矩阵趋于奇异时，结构承载能力就达到了极限，此时的外荷载即为极限荷载[9]。

全过程分析通过逐级增加工作荷载集度来考察结构的变形和受力特征，一直计算至结构发生破坏。通常采用荷载增量法来求解出结构在承受荷载全过程中的荷载—位移(P-Δ)曲线，从而确定结构的极限荷载。整个结构的增量方程为：

(0[K]0+0[K]σ+0[K]L){Δu}i={ΔP}i

(5)

式中:0[K]0，0[K]σ和0[K]L分别为t=0时刻的结构的弹性刚度矩阵、几何刚度矩阵和初位移刚度矩阵，{Δu}i为第i次加载 {ΔP}i时产生的节点位移增量。

1.2现行规范对拱桥结构稳定的要求

现行规范通常要求拱桥的弹性特征值安全系数不小于4，而对于非线性稳定安全系数并没有非常明确的规定。规范[10]要求对钢管混凝土拱桥进行空间稳定性分析，且其弹性特征值安全系数不应小于4.0；对于特大跨径的钢管混凝土拱，由于其材料非线性或几何大变形或双重非线性对结构整体稳定影响较大，一般还应进行考虑非线形的极值点稳定计算。规范[11]与规范[10]关于弹性特征值稳定安全系数的规定基本相同，但规范[11]同时还对非线形整体稳定安全系数提出参考安全值，一般要求其不小于2.0。规范[12]要求对拱肋(拱圈)平面内的稳定性进行检验，按照其承受最大水平推力的中心受压杆件进行检算，其稳定安全系数不得小于4～5，必要时还应检算拱肋平面外的稳定性。另外，文献[13]指出，对于跨径大于200m的钢管混凝土拱桥，其整体弹性稳定系数不小于4.0；其稳定极限承载能力要考虑材料的非线性和几何非线性的影响，极限承载能力与设计荷载之比不宜小于2.0。

实际工程中的桥梁结构失稳多属于第二类稳定问题，但无论是第一类失稳还是第二类失稳，对于相同受力状态下的同一结构，两类失稳对应的可靠指标应是一致的，且应保证结构可靠指标不小于目标可靠指标[14]。另外，文献[14]还指出，第1类稳定安全系数取4时，并不能保证结构实际发生的第2类失稳的可靠指标达到目标可靠指标，因此，若采用第一类失稳模式进行结构稳定性验算，相应的稳定安全系数的取值应重新审视。

2工程实例

本文以艾溪湖大桥为工程实例，该桥为一座三跨连续外倾式拱梁组合桥梁，全长168m，中间主跨的跨径为108m，两边跨的跨径均为30m。主跨的车行道全宽为31m，两侧非机动车道道宽由端部的5m按曲线渐变至跨中的7.5m。图1和图2分别为艾溪湖大桥的平面图和立面图。

该桥的主梁为钢箱结构，分为主跨和副跨两部分，即机动车道的钢箱梁为主跨，两侧非机动车道的钢箱梁为副跨。钢箱拱肋由主拱和装饰拱组成，两者的拱轴线均为抛物线，装饰拱不参与结构受力；主拱的横截面为变截面，截面尺寸由拱脚处的2.5m×2m(宽×高)渐变至拱顶处的1.5m×1.3m；拱肋平面向外倾斜，斜度为3:1，两片倾斜拱肋之间不设置横向支撑。吊杆分为内吊杆和外吊杆两种类型，内、外吊杆的纵向间距均为4m；内吊杆共计25对，与车行道钢箱梁上的吊点相连，参与承担恒载及车行活载；外吊杆共计21对，与人行道钢箱梁上的吊点相连，参与承担恒载及人行活载；需要指出的是，该桥的内吊杆和外吊杆均与拱肋平面成一定夹角。系杆布置在车行钢箱主梁内部，用于平衡拱肋拱脚处的水平推力，共计4组系杆，每片拱肋两组。

单位：cm图1　艾溪湖大桥立面图Fig.1 Elevation of Aixi Lake bridge

单位：cm图2　艾溪湖大桥平面图Fig.2 Plan of Aixi Lake bridge

3桥梁结构稳定性分析

本文应用有限元分析软件ANSYS建立了艾溪湖大桥的空间有限元模型，其钢箱拱肋采用梁单元Beam188进行模拟，该类型单元可考虑大转角、大应变及剪切效应等因素的影响，适宜进行非线性分析[15]；由于钢箱主梁的宽度较大，故将其分成8片分梁，采用梁格法建模，各分梁均采用梁单元Beam188进行模拟；主梁横隔板采用集中质量单元Mass21进行模拟，并计入其质量和质量惯性矩；吊杆和系杆均采用link10单元进行模拟，当出现压应力时，刚度为零，可较好地模拟柔性索的力学性能。

3.1成桥状态时的结构稳定性分析

3.1.1第一类稳定分析

通过有限元分析计算，得到了艾溪湖大桥成桥状态时在6种荷载工况作用下的弹性特征值稳定安全系数，如表1所示。该6种荷载工况作用下的全桥一阶屈曲模态均为拱肋单波面外失稳，图3为工况荷载1作用下的前三阶屈曲模态，可供参考。另外，本文按照基本风速为27.2m/s来计算风荷载，仅考虑主梁和拱肋所受静风荷载中的迎风阻力，忽略了升力和扭矩的影响，相关计算可参考规范[16]。

表1　弹性特征值稳定安全系数

(a)一阶失稳模态；(b)二阶失稳模态；(c)三阶失稳模态图3　工况荷载1作用下的全桥屈曲模态Fig.3 Bridge buckling modes under load condition 1

由表1中的计算结果可以看出，以上6种荷载工况作用下的成桥稳定安全系数均在18以上，满足通常拱桥第一类稳定安全系数不小于4～5的要求；在成桥恒载的基础上再考虑风荷载的作用时，桥梁的稳定安全系数变化不大，可见风荷载对本桥的第一类稳定计算结果影响不大；在成桥恒载的基础上再考虑活载的作用时，该桥的稳定安全系数明显降低，表1中荷载工况2对应的安全稳定系数比荷载工况1降低了13.3%，表明活载对桥梁结构的稳定性影响较大。

3.1.2第二类稳定分析

第1类稳定理论建立在理想的线弹性、小位移理论基础之上，虽然其理论清晰，计算方便，但其计算得到的临界荷载值通常高于结构失稳的实际临界荷载值。而第2类稳定分析理论建立在结构非线性、大位移理论基础之上，它考虑了结构变形和材料弹塑性对结构稳定性的影响[9,17]。本文利用第3类稳定分析理论，分别考虑了几何非线性因素和材料非线性因素的影响，对艾溪湖大桥的进行了极限承载力分析。

采用非线性有限元理论对艾溪湖大桥主桥进行几何非线性分析，只考虑拱桥恒载作用，得到了拱顶处面外位移的P-Δ曲线，如图4中曲线a所示，图中λ为荷载系数，它是所施加的荷载与设计荷载之间的比值，其最大值即为稳定安全系数K。

由P-Δ曲线(曲线a)可以看出，曲线起始段的荷载(系数)与位移之间呈线性关系，随着荷载的不断增加，非线性关系逐渐显现，在接近极限荷载时，位移迅速增加，曲线基本呈水平状。考虑几何非线性后的稳定安全系数为17.911，而弹性特征值稳定安全系数为21.145，相比下降了15.3%，由此可知，对于本文算例而言，几何非线性因素对结构稳定性计算具有重要影响。

图4　荷载—位移曲线(P-Δ曲线)Fig.4 Load-displacement curves (P-Δcurves)

由于艾溪湖大桥的前三阶屈曲模态均为拱肋面外失稳，因而在进行材料非线性分析时，只需考虑钢箱拱肋的材料非线性。考虑材料非线性因素对结构稳定性的影响，其主要问题就是材料本构关系的选取。钢箱拱肋采用Q345D钢材，其屈服强度fy=345MPa，本文采用双线性理想弹-塑性模型来模拟钢材的本构关系[2]，其应力-应变关系为：

(6)

式中：fy为钢材屈服应力；εy为钢材屈服时对应的应变。

利用上述拱肋钢材的本构关系模型，对艾溪湖大桥进行材料非线性分析，只考虑拱桥恒载作用，得到拱顶处面外位移的P-Δ曲线，如图4中的曲线b所示。考虑材料非线性后的稳定安全系数为8.041，相比弹性特征值稳定安全系数下降了62%，由此可知，对于本文算例，材料非线性因素的对结构稳定性分析结果影响巨大，比几何非线性因素更为显著，不可忽略。

通过以上分析得知，几何非线性因素和材料非线性因素对结构稳定的分析结果均有重要影响，因此在对结构稳定性进行分析时，应同时考虑双重非线性的影响。对艾溪湖大桥进行双重非线性分析，只考虑拱桥恒载作用，得到拱顶处面外位移的P-Δ曲线，如图4中曲线c所示。考虑双重非线性后的稳定安全系数为7.265，相比弹性特征值稳定安全系数下降了65.6%，由此可知，一定要同时考虑材料非线性因素和几何非线性因素的影响，才能得到较为可靠的稳定分析结果。

3.2吊杆张拉施工过程中的结构稳定性分析

对于吊杆张拉施工而言，选择合理的张拉方案至关重要，合理的吊杆张拉方案应使张拉过程结构所经历的一切中间状态均满足结构的内力、变形及机具承载力的要求，并最终达到预先要求的目标设计状态，简而言之，它是一条达到指定目标状态的合理(最优)路径。但是，仅考虑吊杆张拉过程中结构的受力和变形是不够的，结构稳定性也应充分考虑，尤其是拱肋的稳定性。对于桥梁工程而言，结构的最不安全状态不一定出现在成桥运营阶段，相反起控制作用的结构状态往往出现在施工阶段，而且很多情况下，结构在施工过程中的稳定性要低于成桥的稳定性，因此，有必要对艾溪湖大桥在吊杆张拉施工过程中的结构稳定性进行分析[18]。

本文假定艾溪湖大桥可在不设置拱肋间临时横撑或支架支护的情况下进行吊杆张拉施工，并选取了3种不同的吊杆张拉方案进行对比分析，此3种吊杆张拉方案分别是：

1)张拉方案1：由拱顶区至拱脚区依次对称张拉吊杆；2)张拉方案2：由拱脚区至拱顶区依次对称张拉吊杆；3)张拉方案3：由四分区开始交替对称张拉吊杆。

此3种吊杆张拉方案均采用先张拉内吊杆，而后张拉外吊杆的模式，共需张拉24组次吊杆。此3种张拉方案对应的具体的吊杆张拉顺序和吊杆施工张拉力分别下表2所示，吊杆编号见上图1，另外，表2中的“N”表示内吊杆，“W”表示外吊杆。

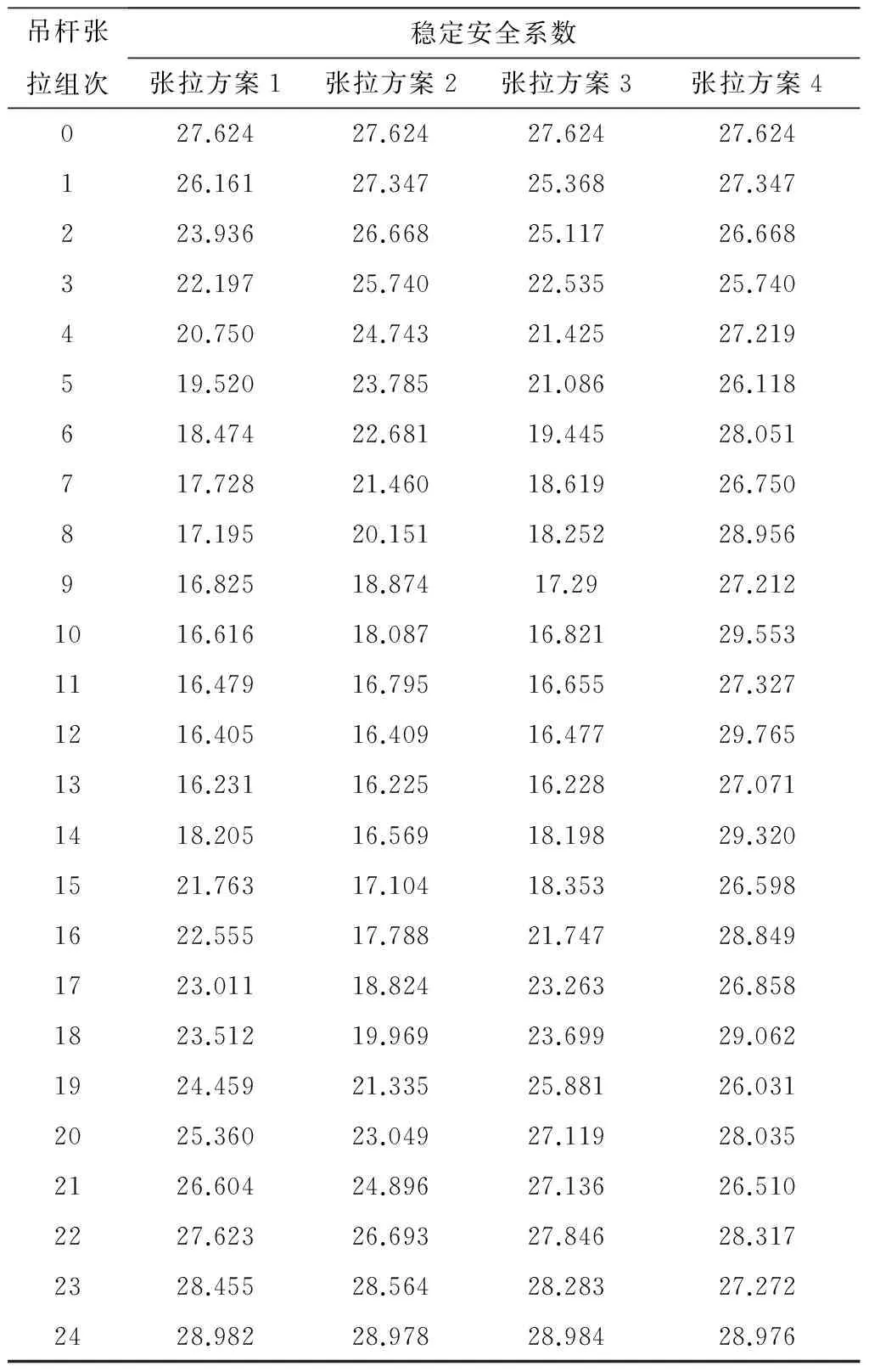
通过有限元建模来模拟吊杆张拉过程，并计算得到了每一组次吊杆张拉完成后的结构稳定安全系数，如图5和表3所示。图5和表3中的“0吊杆张拉组次”表示吊杆张拉前的结构状态，即裸拱状态，作为吊杆张拉的起点，3种张拉方案在裸拱状态下的稳定安全系数同为27.624。

由图5可见，吊杆张拉方案1，方案2和方案3对应的结构稳定安全系数变化曲线的前半段均呈单调递减趋势，表明随着内吊杆的张拉，结构的稳定性逐渐变差，并在内吊杆张拉完毕时(对应吊杆张拉组次13)结构稳定安全系数达到最小值；3种吊杆张拉方案对应的结构稳定安全系数变化曲线的后半段均为单调递增趋势，表明随着外吊杆的张拉，结构的稳定性逐渐变好，并在外吊杆张拉完毕时(对应吊杆张拉组次24)结构稳定安全系数达到最大值。由此可知，虽然外吊杆的索力值相对较小(不及内吊杆的索力值的0.1倍)，但由于其与拱面之间的夹角较大，张拉外吊杆后的结构稳定安全系数显著提高，可见，对于外倾式拱梁组合桥梁而言，外吊杆必不可少，因而发展成为空间多索面体系也成为必然。

图5　吊杆张拉过程中的结构稳定安全系数变化曲线Fig.5 Curves of stability safety coefficients during the suspenders tensioning processes

认真观察图5还可发现，张拉方案一对应的稳定安全系数变化曲线随着内吊杆的张拉先快速下降，但下降速度逐渐变慢，而后随着外吊杆的张拉快速上升，但上升速度逐渐减慢，结合张拉方案一对应的吊杆张拉顺序可知：吊杆越靠近跨中，张拉该组次吊杆对结构的稳定性影响就越大。张拉方案二对应的稳定安全系数变化曲线随着内吊杆的张拉先慢速下降，但下降速度逐渐加快，而后随着外吊杆的张拉先慢速上升，但上升速度逐渐加快，这种现象同样支持上述观点。张拉方案三对应的稳定安全系数变化曲线大致上呈阶梯状，曲线中的快速下降段和快速上升段都对应于拱顶区的吊杆张拉，这种现象依然支持上述观点。

基于以上分析可知，不同的吊杆张拉方案对吊杆张拉施工过程中的结构稳定性有相当程度的影响，张拉方案1、方案2和方案3均采用“先将内吊杆张拉完毕，再进行外吊杆张拉”的模式，导致内吊杆张拉完毕时结构的稳定安全系数降至最低。 本文尝试采用“将内吊杆和外吊杆相互交替张拉”的模式，其具体的吊杆张拉顺序和吊杆施工张拉力如上表2中的张拉方案4所示。张拉方案4对应的张拉过程中的结构稳定系数可见于上表3和图5，在吊杆张拉过程中，结构的稳定安全系数并没有呈现单调递减或递增的现象，而是在27.5附近上下波动，其稳定安全系数的最小值为25.74(对应于吊杆张拉组次3)，比前3种吊杆张拉方案对应的稳定安全系数最小值提高了58.6%，使得吊杆张拉施工过程中结构稳定性显著提高。因此从结构稳定性的角度考虑，吊杆张拉方案4优于张拉方案1、方案2和方案3。

表3吊杆张拉过程中的结构稳定安全系数

Table3Stabilitysafetycoefficientsduringthesuspenderstensioningprocesses

吊杆张拉组次稳定安全系数张拉方案1张拉方案2张拉方案3张拉方案4027.62427.62427.62427.624126.16127.34725.36827.347223.93626.66825.11726.668322.19725.74022.53525.740420.75024.74321.42527.219519.52023.78521.08626.118618.47422.68119.44528.051717.72821.46018.61926.750817.19520.15118.25228.956916.82518.87417.2927.2121016.61618.08716.82129.5531116.47916.79516.65527.3271216.40516.40916.47729.7651316.23116.22516.22827.0711418.20516.56918.19829.3201521.76317.10418.35326.5981622.55517.78821.74728.8491723.01118.82423.26326.8581823.51219.96923.69929.0621924.45921.33525.88126.0312025.36023.04927.11928.0352126.60424.89627.13626.5102227.62326.69327.84628.3172328.45528.56428.28327.2722428.98228.97828.98428.976

以上4种吊杆张拉方案对应的张拉过程中的所有结构暂态的弹性特征值稳定安全系数均满足相关规范不小于4～5的要求，单从此第一类稳定分析的结果考虑，可认为在以上4种吊杆张拉方案对应的张拉过程中的外倾式拱肋稳定性是满足要求的。为安全起见，本文还对吊杆张拉过程的各结构暂态进行了第2类稳定分析，图6为张拉方案1、方案2和方案3对应的第13组次吊杆张拉完毕(即仅内吊杆张拉完毕)时的结构暂态的双重非线性分析结果，其稳定安全系数为5.625，而且其他各结构暂态的第2类稳定安全系数也均满足相关规范不小于2的要求。由此可知，本文考虑的4种张拉方案均满足结构稳定性要求，但以方案4为最优；同时也证明了本桥算例在吊杆张拉过程中无需设置拱肋间的临时横撑或支架等张拉辅助设施。

图6　双重非线性分析得到的P-Δ曲线(K=5.625)Fig.6 P-Δcurve of double nonlinear analysis results (K=5.625)

4稳定性影响因素的参数分析

4.1拱肋矢跨比的影响

对于外倾式拱梁组合体系而言，拱肋的矢跨比是一个重要的参数[19]，矢跨比对桥梁的稳定性具有重要影响。保持艾溪湖大桥拱肋的外倾角和跨度不变，通过改变拱肋矢高来改变矢跨比，计算得到恒载作用下拱肋矢跨比与稳定安全系数之间的关系曲线，如图7所示。

由图7中的曲线可知，存在最优的矢跨比使得桥梁的稳定安全系数达到极大值，该最优矢跨比介于0.20和0.25之间。当拱肋矢跨比较小时，随着矢跨比的增大，特定荷载作用下的拱肋轴向压应力将显著减小，故而稳定安全系数也随之增大；而当拱肋矢跨比较大时，随着矢跨比的增大，拱肋轴向压应力减小不明显，计算长度反而随之显著增大，故而稳定安全系数随之减小。然而，艾溪湖大桥采用的拱肋矢跨比为0.381，显然偏离最优矢跨比较多，从结构稳定安全的角度考虑这并不合理。基于桥梁美学方面的原因，艾溪湖大桥通过采用较大的矢跨比来突出外倾式拱肋的别致造型，但同时这也提高了桥梁的整体造价，造成了景观与效益之间的矛盾。

图7　拱肋矢跨比与稳定安全系数之间的关系Fig.7 Relationship between ratios of height and span and stability safety coefficients

4.2拱肋外倾角的影响

由前文已知，艾溪湖大桥的失稳模态主要是拱肋面外失稳，而拱肋外倾角是引起拱肋承受面外荷载的主要原因之一，因而其对拱肋稳定性有重要影响[20]。保持艾溪湖大桥拱肋的矢高和跨度不变，仅改变其拱肋外倾角度，计算得到了恒载作用下拱肋外倾角度与桥梁稳定安全系数之间的关系曲线，如下图8所示。

图8　拱肋外倾角与稳定安全系数之间的关系Fig.8 Relationship between camber angles of arch rib and stability safety coefficients

由图8中的曲线可知，随着拱肋外倾角的不断增大，桥梁的稳定安全系数随之下降，而且下降速度不断加快。由此可知，拱肋的外倾角对其稳定性并无积极影响，该桥之所以设置18.435。的外倾角度，完全是基于桥梁美学方面的原因。

4.3拱肋刚度的影响

对于外倾式拱梁组合桥梁而言，为了达到其美学效果，拱肋的矢跨比和倾角通常难以进行过多的优化，因而只能从拱肋的截面特性着手来改善结构的稳定性[19]。本文通过改变艾溪湖大桥拱肋的刚度，计算得到了恒载作用下拱肋刚度与桥梁稳定安全系数之间的关系曲线，如下图9所示。

图9　拱肋刚度与稳定安全系数之间的关系Fig.9 Relationship between section rigidities of arch rib and stability safety coefficients

由图9中的曲线可知，随着拱肋面内抗弯刚度的增大，稳定安全系数随之增大，但增幅并不明显，当拱肋面内刚度增大至原来的2倍时，桥梁的稳定安全系数仅仅增大了5.9%；随着拱肋面外抗弯刚度的增大，稳定安全系数也随之增大，且增幅较为明显，当拱肋面内刚度增大至原来的2倍时，桥梁的稳定安全系数增大了20.1%。由此可知，可通过增加拱肋面外抗弯刚度的方法来改善结构稳定性，但随着拱肋面外抗弯刚度的增大，其对稳定性的影响越来越不明显。

5结论

1)艾溪湖大桥的弹性特征值稳定安全系数满足通常规范不小于4～5的要求，由于其外倾式拱肋承受了较大的面外荷载且桥面系的刚度较大，桥梁的失稳模态主要表现为拱肋面外失稳。

2)对于外倾式拱梁组合桥梁而言，空间多索面形式是使外倾式拱肋稳定的有力保障，艾溪湖大桥的拱肋在内、外吊杆的共同作用下，其稳定性显著提高。

3)在吊杆张拉施工过程中，选择不同的吊杆张拉方案对张拉施工过程中结构稳定性有较大影响，艾溪湖大桥的外吊杆对结构稳定性影响较大，采用内吊杆和外吊杆相互交替张拉的吊杆张拉方案可显著提高张拉施工过程中的结构稳定性。

4)由于桥梁美学方面的原因，艾溪湖大桥的拱肋采用了外倾形式和较大的矢跨比，但是这些对其结构的稳定性均产生了不利影响，可通过提高拱肋刚度的方式，尤其是拱肋面外抗弯刚度，来改善其结构稳定性。

参考文献：

[1] 易云焜. 梁拱组合体系设计理论关键问题研究[D]. 上海：同济大学, 2007.

YIYunkun.Key-problemstudyfordesigntheoryofbeam-archassociationbridges[D].Shanghai:TongjiUniversity, 2007.

[2] 谭红霞,陈政清,封周权. 刚构-单拱肋组合桥梁的稳定性研究[J]. 振动与冲击, 2008,27(12):122-125.

TANHongxia,CHENZhengqing,FENGZhouquan.Stabilityofcombinativebridgewithrigidframeandsingle-ribbedarch[J].JournalofVibrationandShock, 2008, 27(12):122-125.

[3]RenWeixin,ZhaoTong,IssamE.Analysisofsteelarchbridge[J].JournalofStructureEngineering, 2004,130(1):1022-1031.

[4]DouC,GouYL,ZhaoSY.Elasticout-of-planebuckingloadsofcircularsteeltubulartrussarchesincorporatingshearingeffects[J].EngineeringStructure, 2013, 52:697-706.

[5] 季日臣,石明星. 大跨度铁路钢管混凝土系杆拱桥稳定性分析[J]. 振动与冲击, 2011,30(8):87-91.

JIRichen,SHIMingxing.StabilityanalysisoflongspanrailwayCESTtied-archbridge[J].JournalofVibrationandShock, 2011, 30(8):87-91.

[6] 陈淮,杨磊. 湛河提篮式拱桥空间弹性稳定性分析[J]. 铁道科学与工程学报, 2013,10(2):1-4.

CHENHuai,YANGLei.SpatialelasticstabilityanalysisoftheZhanheX-stylearchbridge[J].JournalofRailwayScienceandEngineering, 2013, 10(2):1-4.

[7] 王艳,陈淮. 大跨径钢管混凝土桁架拱桥稳定性分析[J]. 铁道科学与工程学报, 2010,7(1):7-10.

WANGYan,CHENHuai.Stabilityanalysisoflongspanconcretefiledsteeltubulartrussarchbridge[J].JournalofRailwayScienceandEngineering, 2010, 7(1):7-10.

[8] 李国豪. 桥梁结构稳定与振动[M]. 北京：中国铁道出版社, 2003.

LIGuohao.Stabilityandvibrationofbridgestructure[M].Beijing:RailwayPublishingHouseofChina, 2003.

[9] 项海帆. 高等桥梁结构理论[M]. 北京：人民交通出版社, 2013.

XIANGHaifan.Advancedtheoryofbridgestructure[M].Beijing:ChinaCommunicationPress, 2013.

[10]GB50923—2013,钢管混凝土拱桥技术规范[S].

GB50923—2013,Technicalspecificationforconcretefilledsteeltubulararchbridge[S].

[11]CQJTG/TD66—2011,公路钢管混凝土拱桥设计规范[S].

CQJTG/TD66—2011,Designspecificationforhighwayconcretefilledsteeltubulararchbridge[S].

[12]TB10002.1—2005,铁路桥涵设计基本规范[S].

TB10002.1—2005,Basicspecificationfordesignofrailwaybridgeandculvert[S].

[13] 牟廷敏,庄卫林,梁健,等. 公路钢管混凝土桥梁设计与施工指南[M].北京：人民交通出版社,2008.

MOUTingmin,ZHUANGWeilin,LIANGJian,etal.Guidefordesignandconstructionofhighwayconcretefilledsteeltubulararchbridge[M].Beijing:ChinaCommunicationPress, 2008.

[14] 童小龙,方志. 基于可靠度指标的桥梁结构稳定安全系数研究[J]. 铁道学报, 2014,36(10):102-108.

TONGXiaolong,FANGZhi.Studyonstabilitysafetyfactorofbridgestructurebaseduponreliabilityindex[J].JournaloftheChinaRailwaySociety,2014,36(10): 102- 108.

[15] 王元清,姜波,石永久. 大跨度钢管混凝土拱桥施工稳定性分析[J]. 铁道科学与工程学报, 2006, 3(5):1-5.

WANGYuanqing,JIANGBo,SHIYongjiu.Analysisofstabilityoflong-spanconcretefilledsteeltubearchedbridgeinconstruction[J].JournalofRailwayScienceandEngineering, 2006,3(5):1-5.

[16]JTGD60—2004,公路桥涵设计通用规范[S].

JTGD60—2004,Generalspecificationfordesignofhighwaybridgesandculverts[S].

[17] 崔军,王景波,孙炳楠. 大跨度钢管混凝土拱桥非线性稳定分析[J]. 哈尔滨工业大学学报,2003,35(7):876 -878.

CUIJun,WANGJingbo,SUNBingnan.Nonlinearbuckinganalysisforlargespanconcretefilledsteeltubearchbridge[J].JournalofHarbinInstituteofTechnology, 2003,35(7):876-878.

[18] 应明,郑一峰,王德军. 吊杆张拉过程中的拱肋稳定性分析[J]. 哈尔滨工业大学学报, 2011,43(4) :142- 144.

YINGMing,ZHENGYifeng,WANGDejun.Stabilityanalysisofarchribintheprocessofdrawingboom[J].JournalofHarbinInstituteofTechnology, 2011,43(4):142-144.

[19] 李雅香. 城市非对称外倾拱肋钢拱桥受力特性研究[D]. 成都：西南交通大学,2011.

LIYaxiang.Amechanicalcharacteristicsstudyonurbansteelarchbridgeswiththeasymmetrictiltarch[D].Chengdu:SouthwestJiaotongUniversity, 2011.

[20] 陈淮,孙应桃. 斜靠式拱桥拱肋倾角变化对稳定性能的影响[J]. 铁道科学与工程学报, 2009,6(1) :21- 24.

CHENHuai,SUNYingtao.VariationalslopingangleofarchribinfluencedonthestabilityofdoubleX-shapedarchbridge[J].JournalofRailwayScienceandEngineering, 2009,6(1):21-24.

Stability analysis of external slanted arch-beam combination bridges

FU Jinlong,HUANG Tianli,XIA Zhi

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract:The external slanted arch-beam combination bridge is a new type of bridge, and the stability problem of its external slanted arch is significant. This paper took the Aixi Lake Bridge located in Nanchang city as the real-world engineering project and established the spatial finite element model of the bridge accordingly. In combination with the existing stability analysis theories for arch bridges, the stability of the Aixi Lake Bridge was analyzed with the process of suspenders tension and the completed bridge state taken into account. The analysis results indicate that the bucking mode of the bridge is mainly shown by out-plane bucking of the arch rib, and that the influence of geometrical nonlinearity and material nonlinearity on the stability of the bridge is significant. Adopting the pattern of tensioning inner-suspenders and outer-suspenders sequentially can improve the stability level of the bridge during the process of suspender tension. The outer-suspenders have positive impacts on the stability of the bridge; therefore, adopting the form of spatial multi suspenders system can improve the stability level significantly. Furthermore, through a number of calculations and analyses, the effects of geometrical parameters of arch rib, such as the ratio of height to span, camber angle and section rigidity, on the stability of the bridge are revealed with several insightful conclusions drawn. The findings in this paper can provide useful reference and guidance for similar projects.

Key words：external slanted arch rib; stability analysis; elastic buckling; nonlinearity; completed bridge state; suspenders tensioning process; parameters analysis

收稿日期：2015-11-29

基金项目：国家自然科学基金资助项目(51478472);湖南省自然科学基金资助项目(2015JJ2176);英国牛顿基金资助项目(Reference NRCP/1415/14)

通讯作者：黄天立(1977-)，男，湖南长沙人，副教授，博士，从事桥梁工程研究；E-mail: htianli@csu.edu.cn

中图分类号：U448.22

文献标志码：A

文章编号：1672-7029(2016)05-0853-10