加筋土挡墙的动力仿真分析

李澄宙

(深圳市龙岗区 工程质量监督检验站，广东 深圳 518172 )

加筋土挡墙的动力仿真分析

李澄宙

(深圳市龙岗区 工程质量监督检验站，广东 深圳 518172 )

摘要:结合室内动力模型试验，开展加筋土挡墙的动力仿真分析,并编制相应的有限元法时程分析计算程序。在建模过程中采用界面单元有效模拟墙内土体与筋条及面板之间在动力荷载下的相互作用。有限元分析结果与模型试验结果吻合良好；揭示了筋条动拉力增量随动荷载增加的变化趋势；并表明墙内土体在承受动荷载作用时，其内质点对地面加速度有明显的放大效应。研究结果可为地震区加筋土挡墙的动力设计提供一定的参考。

关键词：加筋土挡墙；模型试验；动力分析；有限元法

土是一种宜压不宜剪的材料。为提高土体的强度及整体稳定性，法国工程师Henri Vidal[1]于20世纪60年代提出可在土中掺入一定的加筋材料，并于1963年发表了相关的加筋方法和设计理论。由于其良好的抗剪性能，加筋土很快在挡土墙工程中得到了应用(Prageres, 1965)。至此之后，国内外迎来了关于加筋土挡墙研究和应用的热潮[2-9]。我国有着广阔的地震活动地带。加筋土挡墙也广泛地被运用于地震活动地区的公路、铁路、建筑和水利等工程实际中。目前，国内外对加筋土挡墙的研究多集中在其静力学行为方面，对其在地震作用下的动力性能认识还不够深入，使得这一经济合理的工程结构在应用上受到一定的限制。目前对地震区加筋土挡墙的分析研究主要有以下3种方法：1)以单质点在地震过程中的反应为基础来进行分析，称为反应谱法；2)假定加筋土结构内部存在一个滑动破裂面，破裂面把整个墙体分割成2个刚体，墙体承受均匀的与地面运动相同的加速度，忽略加筋土挡墙本身的振动特性，笼统地采用一个不变的地震荷载系数进行分析，称之为拟静力法；3)把整个加筋土挡墙在时间和空间离散，用有限单元法对挡墙进行动力分析，称为有限元法时程分析法。相比于反应普法和拟静力法，有限单元法可以通过运用界面单元合理模拟墙内土体与筋条及面板之间在动力荷载下的相互作用；其次，随着土体本构模型的不断发展和完善，有限元单元法可以适当将土体的非匀质性和非线性等特性包括到数值分析中。而反应谱法和拟静力法则达不到上述研究的目的。本文在结合室内模型试验结果的基础上，运用有限单元法编制动力时程计算程序对加筋土挡墙的动力特性进行了模拟分析，并得到了一些有用的结果可为地震区加筋土挡墙的动力设计提供一定的参考。

1模型试验简介

模型试验箱建立在MTS伺服式振动台(250 kN)实验系统上。挡墙高度和宽度分别为45 cm和80 cm。墙体填土为西南交大地区干砂，不均匀系数为5.4，砂土详细物理参数见表1。加筋土面板采用十字形硬木板。筋条采用矩形截面铝合金条，尺寸为440 mm(长)× 7 mm(宽) × 0.2 mm(厚)。填制墙体时，每层布置8根筋条，筋条的水平和垂直间距为别为210 mm和 90 mm，且每隔一层筋条设置一根带有应变片的筋条。沿墙高方向布置了2个加速度计以测量墙顶对台底加速度的相对值。所有测点原件均通过数据采集系统与计算机相连并在试验过程中进行动态数据采集。试验时对台面施加6 Hz的水平正弦波激振力，并分别进行了激振力加速幅值从0.1 g，0.2 g，0.3 g连续加载和直接加载到0.3 g(g为重力加速度)的加筋土挡墙动力模型试验。

表1　砂土的物理参数

注：γ，emin，emax，Dr，w分别为砂土的重度，最小孔隙比，最大孔隙比，相对密度和含水量。

2有限元模型

有限元法分析的基本原理是把土体或结构分割成在有限个结点处相连的单元离散体，并对每个单元体用有限个参数描述它的力学特性，再对这些单元体的力学特性叠加得到连续土体或结构的力学特性，由此建立各个物理量间的平衡方程组。由于动力问题中作用在土体或结构上的干扰荷载与时间有关，相应的位移，应变和应力都是时间的函数，因此在建立动力平衡方程时，除静力作用外，尚需考虑动力外荷载，土体惯性力和阻尼力。

2.1动力平衡方程

通常，挡土墙沿墙纵向方向有一定的延伸长度，故而可将数值模拟简化为平面应变问题。若不考虑孔隙水与土骨架之间的相对运动，即把土体整个当成连续介质，可得到土体离散后的动力平衡方程组为：

(1)

(2)

α=λω

(3)

β=λ/ω

(4)

其中λ为阻尼比；ω为振动圆频率，一般取基本自振频率ω1。

此处，运用著名的Wilson-θ直接积分法求解平面应变动力平衡方程组，则式(1)的增量法求解基本形式为：

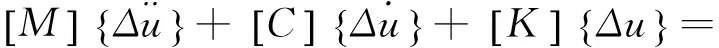
(5)

2.2本构模型

由于动力有限元分析必须包括加筋土挡墙在受动力荷载之前的静力有限元分析，故对本文采用的墙体材料(西南交大地区干砂)需要进行静力性能分析。此处采用非线性的Ducan-Chang双曲线模型进行墙内土体的静力模拟。室内静三轴试验所得砂土的Ducan-Chang模型参数见表2。

表2　砂土的Duncan-Chang模型参数

注：Rf为破坏比；c和φ为土的黏聚力和内摩擦角；n,D,K,F,G为试验常数。

砂土的动力模型采用等价黏弹性模型。通常，除了黏粒含量较大的土类外，黏滞性(流变性)对土的应力应变关系影响不大。但在循环荷载作用下，即使纯净的砂土也表现出明显的类似于黏性土的滞回圈。循环荷载作用下，理想黏弹性体的应力应变滞回曲线为椭圆。等价黏弹性模型将砂土的实际滞回圈用倾角和面积相等的椭圆代替，并由此得到等价黏弹性体的2个基本参数：剪切模量(Gτ)和阻尼比(λ)。本文采用Hardin等人的方法[10-12]将Gτ和λ表示为剪切应变幅的函数并同时考虑静力平均主应力的影响，以此确定相应于任意剪切应变幅的Gτ和λ的值；具体的方法可参见谢定义编著的《土动力学》一书[13]。

铝合金筋条和木制面板的动力特性描述为线性弹性体。用平面应变的有限元法分析加筋土挡墙时，需要将离散分布的筋条和面板转换为连续分布的带状结构；因而在有限元计算中对面板和筋条的弹性模量进行了相应的折减。同时，为模拟墙内土体与筋条及面板之间的相互作用，本文采用无厚度的Goodman[14]单元模拟不同材料之间的接触特性。界面单元的刚度矩阵包含2个待定参数，即界面法向刚度系数(Kn)和界面切向刚度系数(Ks)。对于Kn，若受压，本文取值100 GN/m3，以便忽略2种不同材料相互嵌入的深度；若出现法向拉应力，Kn取为10 kN/m3，以使计算出的接触面拉应力可以忽略不计。对于切向刚度系数Ks，采用界面切应力与界面相对位移的双曲线关系确定，具体可参见Clough和Duncan的方法[15]。

2.3单元类型及边界条件

在加筋土挡墙的有限元仿真分析中，需要对墙内土体，筋条，面板和土体与筋条及面板之间的相互作用选用合适的单元类型进行离散划分。本文采用四结点矩形等参单元划分墙内土体和面板，用等截面杆单元划分筋条，并采用无厚度的Goodman单元模拟土体与筋条及面板之间的相互作用。单元网格划分见图1。左侧和右侧边界约束其水平方向的位移；底部边界则约束其竖直方向的位移。最下面的两层单元沿竖直方向的厚度及其阻尼系数进行了适当的放大，以消除边界处地震反射波的影响。最终的有限元计算程序流程图见图2。

图1　有限元网格Fig.1 Finite element mesh

图2　有限元程序流程图Fig.2 Flow chart of the finite element program

3计算结果与讨论

有限元仿真分析中通过输入SH波模拟地震荷载，并分别计算了输入加速度幅值为0.1，0.2和0.3 g时加筋土挡墙的动力响应特性。

3.1筋条中动拉力增量

模型试验和有限元计算所得筋条最大动拉力增量与其埋深的关系如图3所示。从中可知，有限元分析加筋土挡墙所得结果与实测资料比较吻合，只是在加速度幅值较大(0.3 g)时偏差大一些。有限元分析中，采用的土体静力和动力本构模型虽然都考虑了土体应力应变的非线性特性，但都属于弹性模型。在输入动荷载较小时墙内土体接近为弹性体，采用弹性模型能够较好的模拟其在动力荷载下的响应特性；但当输入动荷载较大时，土体不能完全简化为弹性体，故而弹性本构模型并不能完全反应土体的力学行为。同时，也说明在今后的研究中有必要开展关于加筋土挡墙的弹塑性动力仿真分析。

图3　筋条最大动拉力增量(ΔTmax)Fig.3 Maximum increment of the pullout force of the reinforcement material

从图3中还可看出，在输入地震荷载加速度幅值较小的情况下，加筋土挡墙中筋条的动拉力增量沿墙高方向并没有明显的变化；但当输入荷载的加速度幅值增加到0.3 g时，筋条中动拉力增量沿墙高方向变化较大，墙的底部和腰部处的筋条动拉力增量实测值明显大于其他位置处筋条的动拉力增量，其中以靠近底部处的筋条受动荷载影响更为明显。

3.2加速度放大效应

挡墙内土体加速度放大倍数沿墙高方向的分布示于图4中。从中可以看出，墙内土体各质点相对于地面输入加速度的放大倍数沿离开墙底的距离有增大的趋势。图5为墙顶一点对地面加速度的放大倍数随输入加速度幅值增加的变化关系，其表明墙顶处的加速度放大倍数基本随输入加速度幅值的增加而线性增加。结合图4和图5可知，加筋土挡墙内土体对地面加速度有明显的放大效应。一个理想的具有弹性和线性阻尼的系统，不管其输入的加速度是多少，其放大曲线都是一致的，且随加速度的增大而越发明显，这种现象正好说明了砂土的非线性特性，即随着应变的增加，弹性模量降低，阻尼比增大。

图4　沿墙高方向加速度放大倍数Fig.4 Amplification of the acceleration along the wall height direction

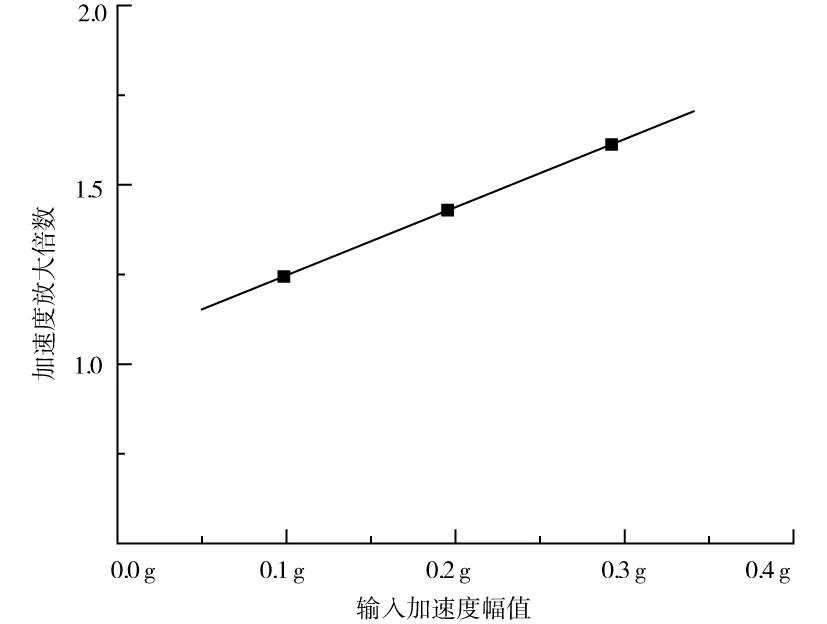
图5　墙顶处加速度放大倍数Fig.5 Amplification of acceleration at the top of the retaining wall

4结论

1) 在地震荷载输入加速度较小时，加筋土挡墙内土体接近弹性体，有限元计算结果与模型试验结果吻合良好；当地震荷载输入加速度较大时，弹性本构模型并不能完全反应土体的动力响应特性，今后有必要开展关于加筋土挡墙的弹塑性动力仿真分析。

2)在地震荷载输入加速度较小时，挡墙中筋条的动拉力增量沿墙高方向没有明显变化；但当输入加速度幅值增加一定值时(模型试验及其有限元分析中该值为0.3 g)，墙体底部和腰部处实测的筋条动拉力增量明显大于其他位置处筋条的动拉力增量，且靠近底部处的筋条受动荷载影响更为明显。

3)加筋土挡墙在地震荷载作用下，其内部土体对地面输入加速度有明显的放大效应，且墙顶一点对地面加速度的放大倍数基本随输入加速度幅值的增加而线性增大。

参考文献

[1] Vidal H. The principle of reinforced earth [R]. Highway Research Board, National Research Council, Washington D C, 1969: 1-24.

[2] Lee K, Chang N. Predictive modeling on seismic performances of geosynthetic-reinforced soil walls [J]. Geotextiles and Geomembranes, 2012, 35: 25-40.

[3] de la Fuente A, Aguado A, Molins C, et al. Innovations on components and testing for precast panels to be used in reinforced earth retaining walls [J]. Construction and Building Materials, 2011, 25(5): 2198-2205.

[4] 杨果林，李海深，王永和. 加筋土挡墙动力特性模型试验与动力分析 [J]. 土木工程学报, 2003, 36(6): 105-110.

YANG Guolin, LI Haishen, WANG Yonghe. Model test on reinforced earth retaining wall under repeated load [J]. China Civil Engineering Journal, 2003, 36(6): 105-110.

[5] 刘华北. 地震作用下模块式面板土工合成材料加筋土挡墙的内部稳定分析 [J]. 岩土工程学报, 2008, 30(2): 278-283.

LIU Huabei. Internal stability analysis of segmental geosynthetic-reinforced soil retaining walls subjected to seismic loading [J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 278-283.

[6] 李昀，杨果林，林宇亮. 土工格栅加筋土挡墙地震响应分析 [J]. 铁道科学与工程学报, 2009, 6(3): 22-27.

LI Yun, YANG Guolin, LIN Yuliang. Analysis on seismic behavior of geogrid-reinforced retaining wall subjected to seismic loading [J]. Journal of Railway Science and Engineering, 2009, 6(3): 22-27.

[7] 江金发. 基于修正容重增加法的加筋土挡墙稳定性分析 [J]. 铁道科学与工程学报, 2012, 9(3): 63-67.

JIANG Jinfa. Stability of reinforced soil retaining wall based on the modified gravity increase method [J]. Journal of Railway Science and Engineering, 2012, 9(3): 63-67.

[8] 杨广庆，周亦涛，周乔勇. 加筋土挡墙拉筋轴向应力分布规律研究 [J]. 岩土工程学报, 2013, 35(4): 650-654.

YANG Guangqing, ZHOU Yitao, ZHOU Qiaoyong. Distribution rules of axial stress of reinforcement in reinforced earth retaining wall [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(4): 650-654.

[9] 周健，谢鑫波，姜炯，等. 包裹式加筋土挡墙的变形特性及影响因素研究 [J]. 岩石力学与工程学报, 2015, 34(1):148-154.

ZHOU Jian, XIE Xinbo, JIANG Jiong, et al. Deformation characteristics and influence factors of wrap reinforced retaining wall [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1):148-154.

[10] Hardin B O, Black W L. Vibration modulus of normally consolidated clay [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1968, 94(2): 353-369.

[11] Seed H B, Idriss I M. Soil moduli and damping factors for dynamic response analyses [R]. Report No. EERC 70-10, Earthquake Engineering Research Center, University of California, Berkeley, California, 1970.

[12] Hardin B O, Drnevich V P. Shear modulus and damping in soils: measurement and parameter effects [J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(6): 603-624.

[13] Goodman R E, Taylor R L, Brekke T L. A model for the mechanics of jointed rock [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1968, 94(3): 637-659.

[14] 谢定义. 土动力学 [M].北京：高等教育出版社，2011.

XIE Dingyi. Soil dynamics [M]. Beijing: Higher Education Press, 2011.

[15] Clough G W, Duncan J M. Finite element analyses of retaining wall behavior [J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(12): 1657-1673.

Numerical simulation on dynamic behavior of reinforced earth retaining wall

LI Chengzhou

(Project Quality Supervision and Inspection Station of Longgang, Shenzhen 518172, China)

Abstract：Based on laboratory model tests, a finite element program (FEP) was developed to analyze the dynamic behavior of a reinforced earth retaining wall. In the FEP, the interaction between the soil and the reinforcement materials was simulated by an interface element. The results obtained via the finite element method agreed well with the model test results. It was revealed that the variation trend of the increment of pullout force of the reinforcement materials increases with the input dynamic force. In addition, under the application of dynamic force, the accelerations of soil elements in the reinforced earth retaining walls were considerably increased as compared to the input acceleration of the ground. The findings of this study can provide useful references for the design of reinforced earth retaining walls in similar earthquake regions.

Key words：reinforced earth retaining wall; model test; dynamic analysis; finite element method

收稿日期：2015-10-29

基金项目：国家自然科学基金重点资助项目(U1361204)

通讯作者：李澄宙(1968-)，男，湖南邵阳人，高级工程师，从事工程质量监督检验检测应用工作与科研工作; E-mail: 1622291890@qq.com

中图分类号：TU365

文献标志码：A

文章编号：1672-7029(2016)05-0848-05