求解工程中静不定结构内力的通用方法

吴晓(湖南文理学院 机械工程学院，湖南 常德，415000)



求解工程中静不定结构内力的通用方法

吴晓
(湖南文理学院 机械工程学院，湖南 常德，415000)

摘要：基于材料力学、结构力学工程中静不定结构内力的求解多采用力法、位移法等方法，静不定结构在外载荷作用下的平衡状态是一个稳定的平衡状态，其应变能存在极小值，故利用静不定结构的多余约束力列出其应变能表达式，引入拉格朗日乘数并结合静力平衡方程，构造拉格朗日函数，对拉格朗日函数求一阶导数并令一阶导数等于 0，即可求得静不定结构的内力，并通过算例予以证明。研究结果表明：此方法适用于求解平面或空间静不定梁、弧形结构、刚架、桁架(包括非线性材料)的约束反力、内力及位移；采用拉格朗日乘数法求解静不定桁架内力的通用性较强，不但可以克服常规方法需利用几何关系建立协调方程的缺陷，而且具有力学概念清晰直观、计算过程简洁、便于工程设计人员在实际中掌握和计算的优点；其所得结果是精确解析解，故可以用于检验其他方法的计算精度。

关键词：静不定；结构；内力；平衡；拉格朗日函数

静不定结构由于承力合理，在实际工程中得到了广泛应用。关于静不定结构内力的求解，材料力学、结构力学等教材多采用力法、位移法进行求解。力法和位移法是计算静不定结构的 2个基本方法。位移法将结点位移选作基本未知量，将结构拆成杆件，再由杆件过渡到结构。位移法适合求解静不定连续梁、静不定刚架。力法是将多余约束力选作基本未知量，将静不定结构拆成静定结构，再由静定结构过渡到静不定结构。力法适合求解静不定连续梁、静不定刚架、静不定圆弧结构、静不定桁架。但是力法求解静不定结构需补充变形协调方程，对如何补充变形协调方程较困难。文献[1−2]采用有限元法研究了不同模量桁架的内力。文献[3]采用余弦函数研究了一般杆系结构节点位移的计算。文献[4]采用位移法求得了外荷载作用下多杆汇交问题的通解，认为避免了需要列出几何关系可以求解的困难，但事实上，文献[4]还是利用杆件变形的几何关系补充变形协调方程进行计算。文献[5]采用矢量分析法研究了节点位移的计算，文献[6]采用速度投影法研究了静定和静不定杆系统结构中节点位移的计算。文献[7]采用纯数学运算研究了超静定桁架中建立变形几何方程的解析法。文献[8−9]采用微分解析法研究了超静定桁架变形协调方程。本文作者采用拉格朗日函数系统研究如何求解平面或空间静不定梁、弧形结构、刚架、桁架(包括非线性材料)的约束反力及内力，并通过算例分析证明：若采用拉格朗日函数求解静不定结构内力，则无需补充变形协调方程。

1　拉格朗日函数的构建

静不定梁、圆弧形结构、刚架主要采用力法、位移法等方法求解约束反力及内力。由于内部静不定桁架是指桁架本身静不定，而 外部静不定桁架本身静定，支座约束反力作用使桁架变成静不定。求解静不定桁架的方法较多。当外力作用在静不定结构上时，其应变能可用支承约束反力或杆件内力表示为U(R1,R2,L,Rn)，静力平衡方程或节点处平衡方程为Qj(R1,R2,L,Rn)。由 于静不定结构在外荷载作用下的平衡是稳定平衡，因此，应变能 U(R1,R2,L,Rn)取极小值时的变量就是静不定结构约束反力或内力。由以上分析可知，求静不定结构约束反力或内力，是求解任意有限多自变量多元函数在任意有限多个约束条件下的极小值问题。数学分析及相关专著一般仅对二元函数在多个约束条件下的极值问题采用拉格朗日函数进行求解和证明，而未对有限多个自变量多元函数在任意有限多个约束条件下极值问题求解。因此，本文对采用拉格朗日函数求解此类问题进行证明，并通过算例说明本文方法的应用。

利用静不定结构应变能函数及静力平衡方程或节点静力平衡方程，可构造如下拉格朗日函数：

将式(1)对自变量求一阶导数可得：

式中：i=1,2,L ,n ；j=1,2,L ,m ；λj为拉格朗日乘子。由式(1)和式(2)可知：要求式(1)的极小值解，只需求解方程组式(2)。

由拉格朗日函数式(1)及静力平衡方程式(2)，可知始终有下式成立：

所以，由式(3)和式(4)可知恒有下式成立：

所以，由式(4)和(6)可知恒有下式成立：

由以上充分性及必要性的证明可知：采用拉格朗日函数求解任意有限多个自变量多元函数在任意有限多个约束条件下的极小值问题是可行的。

2　求解静不定结构内力

2.1静不定梁内力的求解

算例1求图1所示一次静不定梁的多余约束力。

图1　一次静不定梁Fig.1　Statically indeterminate beams of the first degree

设A支座的竖向反力和力矩分别为RA和MA(以下类同)，梁的抗弯刚度为EI，梁AB 跨度为l，以 B 点为力矩支点可得

可构造拉格朗日函数为

将式(4)对多余约束力进行一阶偏导可得：

由式(5)可得多余约束力为

式(11)与文献[10]中所得结果是一致的。

算例2计算图2所示一次静不定连续梁的多余约束力。

图2 一次静不定连续梁Fig.2Statically indeterminateContinuous beams of the first degree

以B点为力矩支点可得

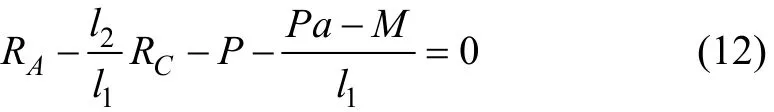
可构造拉格朗日函数为

将式(13)对多余约束力进行一阶偏导可得：

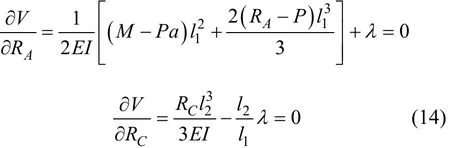
由式(14)可求得多余约束力为

式(15)所示结果与文献[1]中所得结果是一致的。

算例3求图3所示三次静不定梁的多余约束力YA，YB，MA和MB。

由材料力学理论可得以下静力平衡方程：

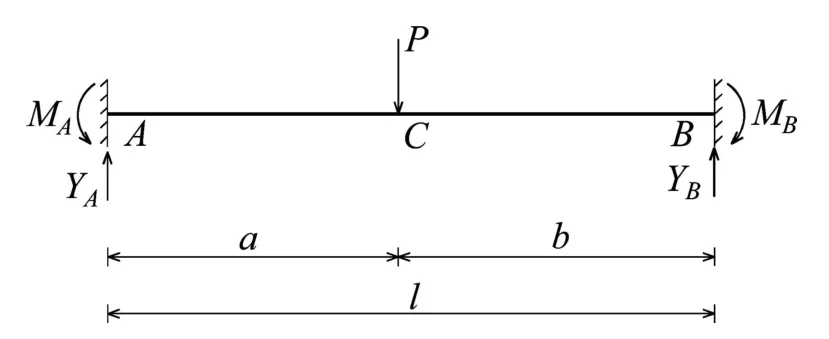
图3　三次静不定梁Fig.3　Statically indeterminate beams of the third degree

可构造拉格朗日函数为

将式(17)对多余约束力进行一阶偏导可得：

由式(18)可以求得多余约束力为：

式(19)所示与文献[11]中结果是一致的。

2.2静不定圆弧内力的求解

算例4求图4所示一次静不定圆弧曲杆的多余约束力。

由材料力学理论可得如下静力平衡方程：

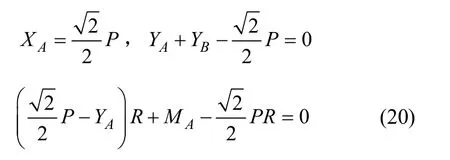
可构造拉格朗日函数为

图4一次静不定圆弧曲杆Fig.4Statically indeterminate arcCurve bar of the first degree

将式(21)对多余约束力进行一阶偏导可得：

由式(22)可以求得多余约束力为

MA=0.353 5PR，YA=0.353 5P(23)

式(23)所示结果与文献[10]中结果是一致的。

2.3静不定刚架的内力求解

算例5求图5所示三次静不定平面刚架的多余约束力。

由材料力学理论可得静力平衡方程为：

可构造拉格朗日函数：

图5　三次静不定平面刚架Fig.5　Statically indeterminate plane rigid frame of the third degree

将式(25)对未知约束力进行一阶偏导可得：

由式(26)可以求得未知约束力为

式(27)所示结果与文献[10]中的结果是一致的。

算例6 求图6所示空间刚架的未知约束力。

对于图6所示刚架 AB 杆受到弯矩、扭矩联合作用，BC杆仅受到弯矩作用。以A为力矩支点可得

可构造拉格朗日函数：

图6　一次静不定空间刚架Fig.6　Statically indeterminate space rigid frame of the third degree

将式(29)对未知约束反力进行一阶偏导可得：

由式(30)可以求得

式(31)所示结果与文献[12]中结果是一致的。

2.4静不定桁架内力的求解

算例7 求图7所示三次静不定平面桁架的内力。l1=l2=l3=l4=l5=l，且各杆材料、面积相同。

节点F处平衡方程为

节点D处平衡方程为

图7　三次静不定平面桁架Fig.7　Statically indeterminate plane truss of the third degree

节点B处平衡方程为

可构造拉格朗日函数

将式(35)对杆件内力Ni进行一阶偏导可得

由式(32)～(36)可以求桁架杆内力及未知约束力为：

在式(37)中令P=240 N时，所得结果与文献[8]中结果是一致的。

算例8对于图8所示静不定桁架，假设静不定桁架所有杆件长度皆为 l，求桁架内力及支承约束反力。

对于图8所示静不定桁架，可知其静力平衡方程为：

利用桁架各节点的平衡方程，可把桁架各杆件内力用支承约束反力表示为：

图8　二次静不定桁架Fig.8　Statically indeterminate triss of the second degree

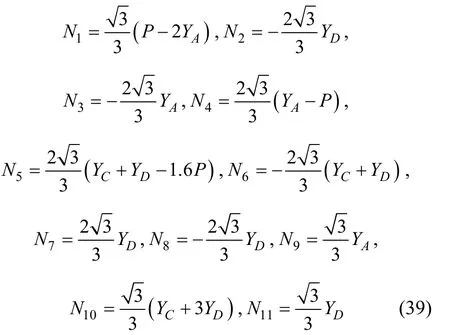
构造拉格朗日函数为

将式(40)对支承约束反力求一阶导数且令一阶导数等于0可得：

利用式(35)和(38)可得：

当P=25 N时，式(42)所示结果与文献[8]中结果是一致的。

算例9图9为一次静不定空间桁架示意图，空间杆系结构由单一结点A通过4个杆与基础相连，假设所有杆材料、截面积、杆长都相同。杆1和杆3位于水平面ABD内，杆 2和杆4位于垂直平面ACE内，截得角度为∠BAD，∠ BAO=∠DAO=∠CAO=α，在 A点的力 P 作用于垂直平面内，与平面 BCD 平行，且与垂直杆 AE 的夹角为 45°，=3a，，，求各杆内力。

空间桁架的内力平衡方程为

图9　一次静不定空间桁架Fig.9　Statically indeterminate space truss of the first degree

可构造拉格朗日函数为

将式(34)对杆件内力Ni进行一阶偏导可得：

利用式(33)和(35)可求得空间桁架内力为：

式(46)结果与文献[13]中结果是一致的。

3　非线性材料桁架变形计算

3.1非线性材料桁架变形能

为了使本文的研究具有一般性，参阅文献[14−15]，可令材料非线性静不定桁架的应力及应变表达式为

式中：B和e(e≥1)皆为常数，且对拉伸和压缩状态均相同；σ 为应力；ε 为应变(由于e≥1，求杆件拉压力时无论拉伸和压缩状态ε 均取绝对值)。材料非线性静不定桁架第i个杆件在拉压力Ni作用下的应变、应力表达式为

式中：Ai为桁架第 i 个杆件的横截面积。由文献[14]可知材料非线性静不定桁架第 i 个杆件的单位体积内应变能ui及单位体积内余能分别为

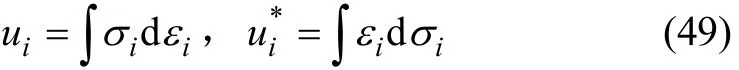
将式(47)和(48)代入式(49)可得：

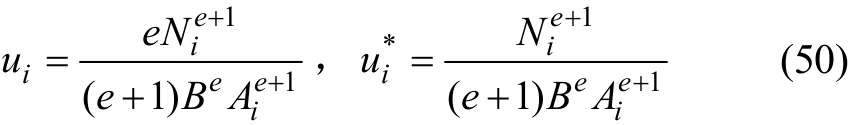
由式(50)可得桁架第 i 杆件的应变能、 余能分别为

式中：li为桁架第i个杆件的杆长。再由式(51)可得材料非线性静不定桁架的应变能、余能分别为

采用式(52)的应变能表达式构造拉格朗日函数要注意：由于求材料非线性静不定桁架杆件拉压力时应变ε 对杆件拉伸和压缩状态均取绝对值，且桁架计算一般假定材料非线性静不定桁架杆件内力全部为拉力，因此，采用应变能表达式求杆件拉压力时，Ni也要取绝对值，否则，求出来的杆件拉压力有可能是复数。使用式(52)所示余能表达式计算材料非线性静不定桁架位移时，不能将杆件拉压力取绝对值，应直接代入杆件拉压力Ni的真实值。

3.2静不定桁架变形的求解

算例10 对于图10 所示 k 个杆件节点汇交构成的材料非线性静不定桁架，令桁架各杆截面积相同，以下算例类同。假定该材料非线性静不定桁架的杆件内力全部为拉力，可得桁架节点平衡方程为：

可构造拉格朗日函数为

将式(54)对内力Ni求一阶导数并令，可得

将式(55)代入式(53)求得 λ1和 λ2，再利用式(55)即可求得图10 所示材料非线性静不定桁架各杆件的拉压内力。

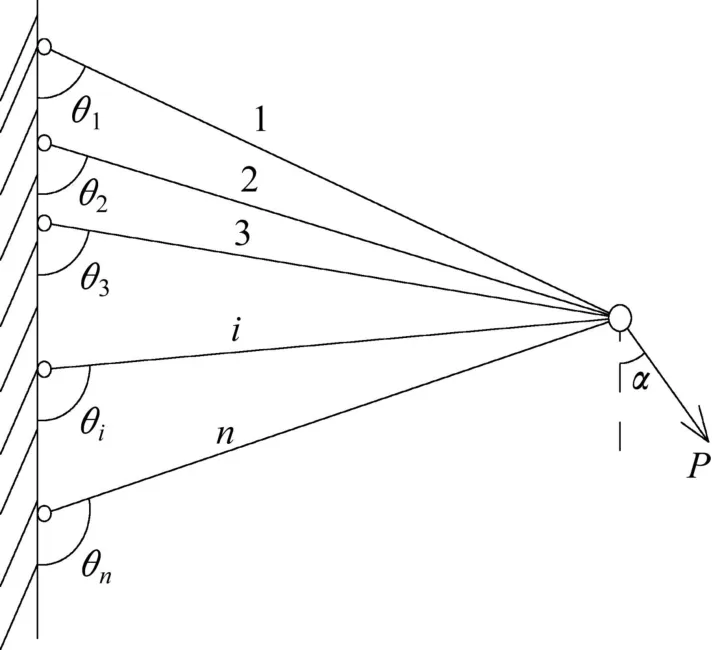
图10　k个杆件静不定桁架Fig.10　Statically indeterminate truss with k-bar

以图11所示非线性静不定桁架为例，假设θ1=45°，θ2=90°，θ3=135°，α=90°，，l2=l，且各杆材料、面积相同。

由图11可得桁架节点D点的平衡方程为

由式(56)可得

由图11及式(57)可判断图11所示材料非线性静不定桁架个杆件皆为拉力，利用式(55)和(56)可得：

由式(59)和(58)可以求得

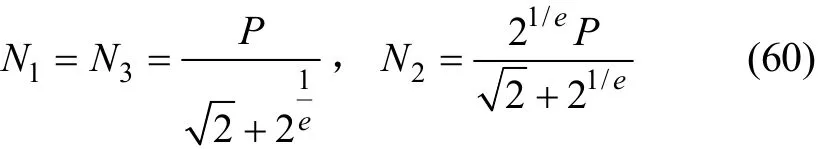
在式(60)中，令 e 为1和2时的结果与文献[14]中的结果完全一致。

图11　3个杆件静不定桁架Fig.11　Statically indeterminate truss with three bars

将式(60)代入式(52)中可得图2所示材料非线性静不定桁架的余能表达式为

利用式(61)将余能 U*函数对外力P求一阶偏导数即可得到图11所示材料非线性静不定桁架节点 D 的水平位移为

算例11对于图12所示材料非线性静不定桁架，可假定该静不定桁架杆件内力全部为拉力。设桁架杆件长度分别为。利用静力平衡方程,可以求得图3所示材料非线性静不定桁架支承反力分别为。

图126个杆件静不定桁架Fig.12Statically indeterminate truss with six bars

利用桁架各节点的平衡方程,可得桁架各杆件内力为

对式(63)进行分析可知N6为拉力，N5为压力，显然N1和N2为压力，N3和N4为拉力。可构造拉格朗日函数为

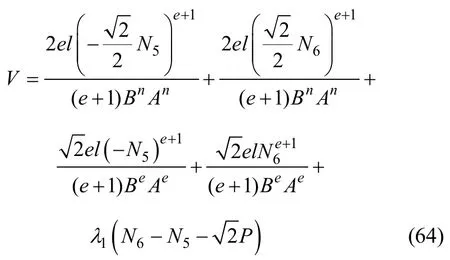
将式(64)对材料非线性静不定桁架杆件的内力 N5和N6求一阶导数且令一阶导数等于0可得

此结果与文献[10]中结果是一致的。

将式(66)代入式(52)可得图12 所示材料非线性静不定桁架的余能表达式为

利用式(67)把余能 U*函数对外力P求一阶偏导数即可得到图12 所示材料非线性静不定桁架节点C 的水平位移为

4　讨论与分析

由算例1至算例 6可知：计算平面、空间静不定梁、圆弧形结构、刚架内力及约束反力，可利用静不定结构的静力平衡方程构造拉格朗日函数。

算例 7和算例8是外部静不定桁架即外部静不定桁架本身是静定但由于支座约束反力作用使桁架变成静不定。计算外部静不定桁架各杆件内力时，若桁架各杆件内力用桁架支座反力全部表示出来，则可利用桁架的静力平衡方程来构造拉格朗日函数；若桁架各杆件内力不用桁架支座反力全部表示出来，则可利用桁架中除支座节点以外的其他各节点处静力平衡方程来构造拉格朗日函数。

算例10至算例12中的内部静不定桁架是指桁架本身静不定。算例10 至算例11的桁架各杆件内力不能用桁架支座反力全部表示出来,计算内部静不定桁架各杆件内力时，仅能利用除桁架支座节点以外的其他各节点处静力平衡方程来构造拉格朗日函数。

由以上算例分析可知：计算静不定梁、圆弧形结构、刚架内力及约束反力时，可利用静不定结构的静力平衡方程构造拉格朗日函数。静不定结构的静力平衡方程个数就是拉格朗日乘子 λj的个数。

计算汇交内部静不定桁架各杆件内力时,仅能利用支座除桁架节点以外的其他各节点处静力平衡方程来构造拉格朗日函数，汇交节点仅有 2个静力平衡方程，汇交内部静不定桁架拉格朗日乘子 λj的个数有2个。

计算外部静不定桁架各杆件内力时，当桁架各杆件内力用桁架支座反力全部表示出来时，则可利用桁架的静力平衡方程来构造拉格朗日函数，静力平衡方程的个数就是拉格朗日乘子 λj的个数; 当桁架各杆件内力不用桁架支座反力全部表示出来时，可利用支座节点除外的桁架其他各节点处静力平衡方程来构造拉格朗日函数,各节点处静力平衡方程个数就是拉格朗日乘子 λj的个数。

从以上算例计算结果可以看出：本文方法还可以计算非线性材料桁架的内力和位移，所得计算结果精度很高，因为采用拉格朗日乘数法求解静不定桁架内力所得到的结果是精确解析解；采用拉格朗日乘数法求解静不定平面、空间静不定梁、圆弧形结构、刚架内力、桁架内力的方法通用性较强，不但可以克服常规方法需利用几何关系建立协调方程的缺陷,而且具有力学概念清晰直观、计算过程简洁、便于工程设计人员在实际中掌握和应用的优点，可以用来检验其他方法的计算精度。

文献[3−4]利用位移法研究了超静定桁架变形协调方程，文献[5−6]本质上都是利用矢量分析法研究超静定桁架变形协调方程，文献[7−9]采用微分研究了超静定桁架变形协调方程。以上方法全部依赖建立变形协调方程求解静不定桁架内力。本文采用拉格朗日乘数法求解静不定桁架内力的方法有固定规律可循，从真正意义上克服了依赖桁架杆件变形几何关系求解静不定桁架内力的困难。

5　结论

1)对采用拉格朗日乘数法求解静不定桁架内力的问题进行了数学证明。

2)计算平面或空间静不定梁、圆弧形结构、刚架内力及约束反力时，可利用静不定结构的静力平衡方程来构造拉格朗日函数。

3)求解内部静不定桁架各杆件内力，仅能利用支座节点除外的桁架其他各节点处静力平衡方程来构造拉格朗日函数。求解外部静不定桁架各杆件内力时，若当桁架各杆件内力用桁架支座反力全部表示出来，则可利用桁架的静力平衡方程来构造拉格朗日函数；若当桁架各杆件内力不用桁架支座反力全部表示出来时，则可利用支座节点以外的桁架其他各节点处静力平衡方程来构造拉格朗日函数。

4)采用拉格朗日乘数法求解静不定桁架内力的通用性较强，不但可以克服常规方法需利用几何关系建立协调方程的缺陷,而且具有力学概念清晰直观、计算过程简洁、便于工程设计人员在实际中掌握和计算的优点，可以用来检验其他方法的计算精度。

参考文献：

[1]张晓月.基于敏度分析的不同模量桁架正反问题求解[D].大连: 大连理工大学工程力学系,2008:1−35.ZHANG Xiaoyue.Sensitivity analysis based numerical solutions of normal and inverse problems of elastic bi-modular truss structure[D].Dalian: Dalian University of Technology.Department of Engineering Mechanics,2008:1−35.

[2]杨海天,张晓月,何宜谦.基于敏度分析的拉压不同模量桁架问题的数值分析[J].计算力学学报,2011,28(2): 237−242.YANG Haitian,ZHANG Xiaoyue,HE Yiqian.Sensitivity analysis based numerical solution for truss structures with bi−modulus[J].Chinese Journal ofComputational Mechanics,2011,28(2): 237−242.

[3]姚顺忠.一般杆系结构节点位移计算方法的探讨[J].西南林学院学报,2002,22(1): 61−63.YAO Shunzhong.Analysis of methodsCalculating displacement of a truss joint[J].Journal of Southwest ForestryCollege,2002,22(1):61−63.

[4]陈平,陈国良,杨绪普.载荷作用下多杆汇交问题的通解[J].力学与实践,2014,36(3): 348−350.CHEN Ping,CHEN Guoliang,YANG Xupu.The general solution of the multi−rod junction problems[J].Mechanics andEngineering,2014,36(3): 348−350.

[5]冯贤桂.结点位移计算的一种简单方法[J].力学与实践,2002,24(1): 49−50.FENG Xiangui.A simple method forCalculating node displacement[J].Mechanics in Engineering,2002,24(1): 49−50.

[6]朱伊德.静定和静不定杆系结构中节点位移的一种计算方法[J].上海应用技术学院学报,2007,7(1): 33−35.ZHU Yide.A method forCalculating node displacement of statically determinate and statically indeterminate structure of bar system[J].Journal of Shanghai Institute of Technology,2007,7(1): 33−35.

[7]倪尔有.超静定桁架中建立变形几何方程的解析法[J].鞍山钢铁学院学报,1991,14(3): 56−59.NI Eryou.Analytic method of setting up deformation geometry equations on statically indeterminate truss problems[J].Journal of Anshan Institute of Iron and Steel Technology,1991,14(3): 56−59.

[8]边文凤,董正筑.超静定桁架变形协调方程的新方法[J].计算力学学报,2002,19(2): 250−252.BIAN Wenfeng,DONG Zhengzhu.A new method for problem of hyperstatic truss[J].Chinese Journal ofComputational Mechanics,2002,19(2): 250−252.

[9]高金华.利用微分方法推导静不定桁架变形协调方程[J].力学与实践,1998,20(5): 67−68.GAO Jinhua.Using differential method to derive deformationCompatibility equation of statically indeterminate truss[J].Mechanics and Engineering,1998,20(5): 67−68.

[10]刘鸿文.材料力学: 下册[M].3版.北京: 高等教育出版社,1999: 57−60.LIU Hongwen.Mechanics of materials: Volume 2[M].3rd ed.Beijing: Higher Education Press,1999: 57−60.

[11]S.铁摩辛柯,J.盖尔.材料力学[M].胡人礼,译.北京: 科学出版社,1990: 237−242.TIMOSHENKO P,GAL J.Mechanics of materials[M].HU Renli,trans.Beijing: Science Press,1990: 237−242.

[12]龙驭球,包世华.支秉堔.结构力学: 上册[M].2版.北京:高等教育出版社,2006: 299−300.LONG Yuqiu,BAO Shihua.Structure mechanics: Volume1[M].2nd ed.Beijing: Higher Education Press,2006: 299−300.

[13]朱伊德,薛芸.空间桁架的单位向量法[J].力学与实践,2008,30(1): 84−86.ZHU Yide,XUE Yun.Unit vector method for space trusses[J].Mechanics and Practice,2008,30(1): 84−86.

[14]孙训方,方孝淑.材料力学: II[M].4版.北京: 高等教育出版社,2002: 64−66.SUN Xunfang,FANG Xiaoshu.Materials mechanics: II[M].4th ed.Beijing: Higher Education Press,2002: 64−66.

[15]R G 巴德纳斯.高等材料力学及实用应力分析[M].西安交通大学材料力学教研室翻译组译.北京: 机械工业出版社,1983: 294−295.BUDNATH R G.Advanced mechanics of materials and the applied stress analysis[M].Translation Group of Staff Room of Mechanics of Materials,Xi’an Jiaotong University,trans.Beijing:China Machine Press,1983: 294−295.

(编辑 陈灿华)

A general method of solutions for engineering statically indeterminate structure force

WU Xiao
(College of Mechanical Engineering,Hunan University of Arts and Science,Changde 415000,China)

Abstract:Force method and displacement method are usually adopted forCalculation of engineering statically indeterminate structure force in materials mechanics and structure mechanics.Because equilibrium state of statically indeterminate structure is a stable one under external load,there are the minimum values for strain energy.Based on the extra restraint force of statically indeterminate structure,the expression of strain energy was presented.With the introduction of Lagrange multiplier andCombined with the static equilibrium equation,the Lagrange function was established.The values of first derivative of Lagrange function were set as 0,and the force values of statically indeterminate structure were gotten.The results show that this method is suitable for the solution of restraint reaction,force and displacement for plane statically indeterminate(or space statically indeterminate),arc structure,steel frame and truss(including nonlinear material).The method of Lagrange multiplier for the solutions of statically indeterminate truss forceCan be widely applied.It overcomes the defects of establishingCoordinate equations by the geometry relations in regular method.The forceConcept isClear,theCalculation is simple and it is easy to be mastered by the engineering technician.As the analytical solution is accurate,itCan be used toCheck theCalculation accuracy obtained by other methods.

Key words:statically indeterminate; structure; force; equilibrium; Lagrange function

中图分类号：O342

文献标志码：A

文章编号：1672−7207(2016)01−0262−11

DOI:10.11817/j.issn.1672-7207.2016.01.036

收稿日期：2015−01−12；修回日期：2015−03−22

基金项目(Foundation item)：湖南省科技计划项目(2011SK3145)；湖南“十二五”重点建设学科项目(湘教发[2011]76 号)；湖南省自然科学基金资助项目(2015JJ6073)(Project(2011SK3145)supported by the Science and Technology Plan of Hunan Province；Project([2011]76)supported by the Hunan“Twelfth Five Year Plan” KeyConstruction; Project(2015JJ6073)supported by the Natural Science Foundation of Hunan Province)

通信作者：吴晓，教授，从事结构振动理论研究；E-mail: wx2005220@163.com