一种滤除衰减直流分量的全波傅氏改进算法研究

2016-06-23吴继维童晓阳廖小君郑永康黄忠胜韩花荣

电力系统保护与控制 2016年2期

吴继维，童晓阳，廖小君，郑永康，黄忠胜，刘涛，韩花荣

(1.西南交通大学电气工程学院，四川成都 610031; 2.国网四川省电力公司技能培训中心，四川成都 610072; 3.国网四川省电力公司电力科学研究院，四川成都 610072)

吴继维1，童晓阳1，廖小君2，郑永康3，黄忠胜2，刘涛3，韩花荣2

全波傅氏算法在提取故障电流中基波分量时受衰减直流分量的影响较大。针对此问题，提出了一种滤除衰减直流分量的全波傅氏改进算法，给出新型衰减直流分量参数估算方法的公式推导。首先利用一个周波内的采样值求出故障电流中衰减直流分量的初始幅值和衰减时间常数，用采样值减去衰减直流分量值得到修正后的采样值，再利用全波傅氏算法计算出基波分量。分别采用静态模型信号、PSCAD/EMTDC 仿真信号检验了该算法的性能。仿真结果表明，所提出的算法能够有效地减少衰减直流分量的影响。与一般改进算法相比，所提算法仅需要一个周波的采样数据，计算量小，计算的基波分量准确性高。

衰减直流分量；参数计算；时间常数；全波傅氏算法；基波分量

0 引言

作为电力系统微机保护中提取基波分量的一种常用算法，全波傅氏算法在电力系统中应用十分广泛。其基本思路来自傅里叶级数，它假定被采样的模拟信号是一个周期性时间函数，除基波外还含有不衰减的直流分量和各次谐波。实际上电流中的直流分量是按指数规律衰减的，由于其频谱的连续性将对傅氏算法带来较大的计算误差。

为了消除衰减直流分量的影响，许多学者提出了大量的算法[1-14]。文献[1]取相邻的三组数据窗，即为采样间隔)，对三个数据窗分别进行全周傅氏变换，得到三组数据窗下各次波的实部和虚部数值及实部和虚部误差的理论分析值，联立方程求解出基波分量的值。文献[2-3]通过小波分析滤除衰减直流分量，充分利用了故障电流信号中的暂态信息。文献[4]假设信号由衰减直流分量和基波分量组成。将基波分量按三角函数公式展开，将衰减直流分量部分用泰勒公式展开并取前两项，得到一组用于基波分量提取的线性滤波器的系数，从而计算出基波分量。文献[5]首先构造了一个数字滤波器，计算衰减直流分量，获得其与实际衰减直流分量的误差，通过两个连续的数据窗计算得到衰减直流分量的时间常数，通过查表得到误差，求出衰减直流分量。最后通过最小二乘法计算基波分量。文献[6-9]用一个周波加一个点的采样数据，精确估计指数函数型衰减直流信号的幅值和时间常数。每个采样数据减去衰减直流分量后，利用全波傅氏算法算得准确结果。文献[10]提出了一种递推离散傅氏算法，在不增加计算量的前提下有效滤除了衰减直流分量的影响。文献[11]通过引入一组滤波算子，通过两次 DFT 变换精确算出采样信号中的各频率分量。文献[12]提出了利用三采样点快速提取基频分量瞬时值的算法。文献[13]通过连续进行三次傅立叶变换计算基波分量，避免了对数运算或指数运算，算法所需数据为一个工频周期采样点数加2个采样点。

在已有研究的基础上，本文提出了一种滤除衰减直流分量的全波傅氏改进算法，首先利用故障后一个周波内的采样值求出故障电流中衰减直流分量的初始幅值和衰减时间常数，然后用各点采样值减去相对应的衰减直流分量得到修正后的采样值，再对它利用全波傅氏算法计算出基波分量。本文算法的不同点是在故障后取7N/8+1个(N为一个工频周期的采样点数)采样点数就能计算出衰减直流分量，在采样点数达到N时准确求出基波分量。

1 衰减直流分量的估计算法

设故障电流的表达式为

式中：0I为衰减直流分量的初始值；t为衰减直流分量的时间常数；hI 、hw 和hj分别为h次谐波的幅值、角频率和相角。在微机保护中，故障电流信号是通过离散采样后进行运算的。当对故障电流进行采样时，设N为一周波采样点数(假设微机保护中N的取值为4的倍数)，T为工频周期，则：

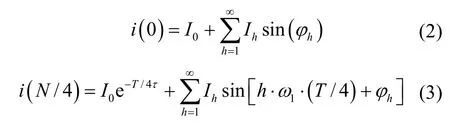
将以上4式相加得

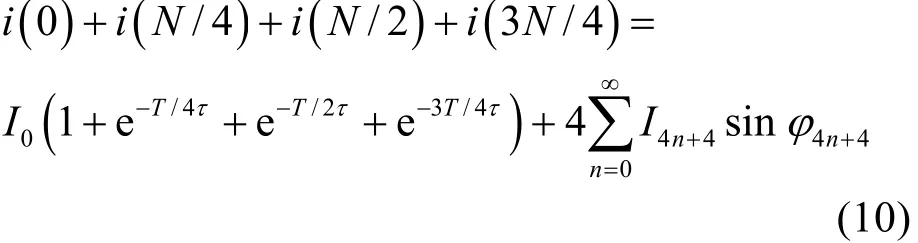
将上式后移N/8个采样点可得

将式(10)与式(11)相加可得

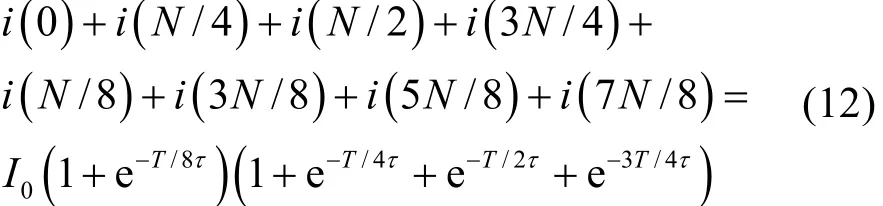
同理可得到

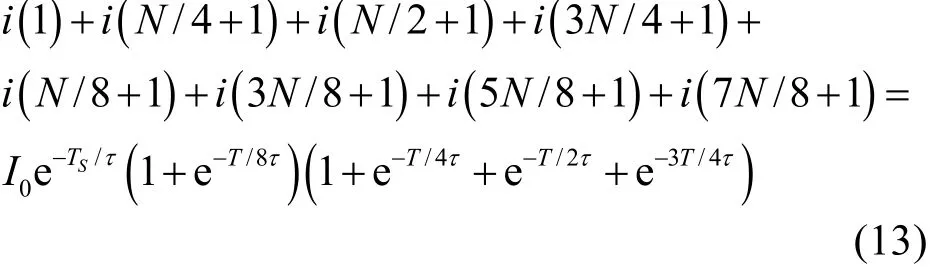
其中，Ts为采样周期，Ts=T/N，分别令

当故障信号中直流分量为一恒定值时，分析以上计算过程可得a b= 、t ¥为。因此当求得a、b之后应进行判断，当a b= 时表明故障信号中所含直流分量为一恒定分量，且恒定直流分量的幅值

但是，ln 函数计算量大，在工程应用中不适宜嵌入式系统的实现[6-7]，对 e-Ts/t进行泰勒展开。

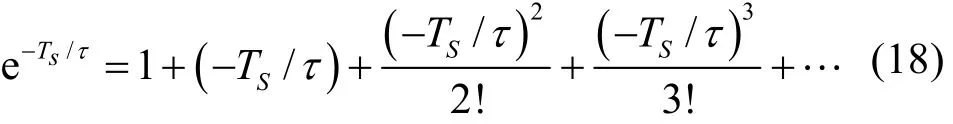
取式(18)的前两项代入式(16)，进行线性处理，得到t的近似简化计算式为

由上式可知根据a、b/a两个值计算出I0，它取决于采样信号采样的准确性与受干扰程度，不受τ近似简化的影响。

2 滤除衰减直流分量的改进全波傅氏算法

由故障电流表达式 (1)可得 ah=Ihsin jh、bh= Ihcosjh， ah和 bh由全波傅氏算法求解得

式中：N为一个工频周期内的采样点数；j为离散采样点序号。各次谐波的幅值为I = a2+ b2。

当求得a = b时，表明故障信号包含一个恒定直流分量，此时用全波N点的每个采样信号减去该直流分量，得到滤除直流分量后的采样值，然后计算得到各次分量。

当求得a ¹ b时，将全波N点的每个采样信号减去采样时刻的衰减直流分量估计值，得到滤除衰减直流分量的采样信号 i¢(j )。由于T与τ都属于同一量级，T/τ可能大于1，因此在计算采样时刻衰减直流分量估计值时考虑取jT泰勒展开式的前10项近似计算，得到式(22)。

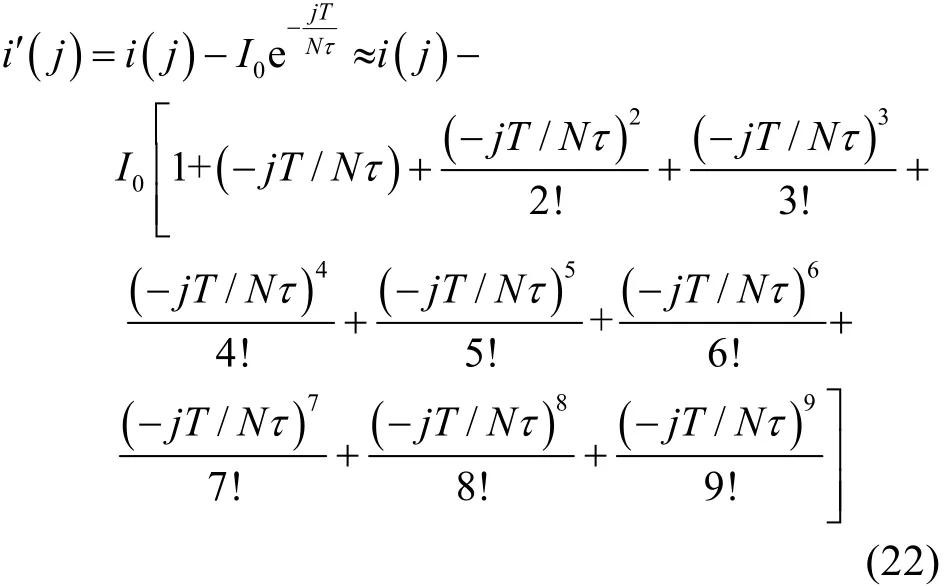
再对 i¢(j )运用全波傅氏算法，可精确计算出故障电流中各次电流的幅值和相角。取式(21)中 h = 1，得到基波的幅值I1和相位 j1。

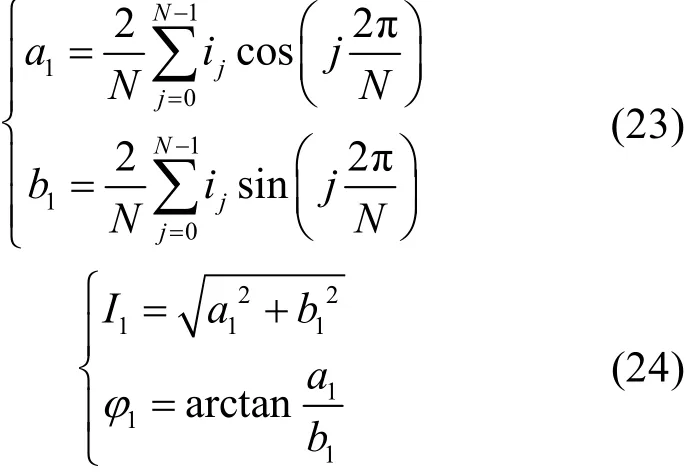
3 算例分析与验证

3.1 静态算例分析与验证

为验证本文算法滤除衰减直流分量的性能，构造故障电流信号i(t)。假设故障电流信号中基波分量经各种变换后对应基准幅值为I1=1.0 A，衰减直流分量初始幅值I0与基波分量幅值I1的比I0/I1分别为0.2、1、和5。2次、3次和5次谐波分量幅值与基波分量幅值的比分别为I2/I1=0.5，I3/I1=0.33，I5/I1=0.2；各次分量的相角分别为 j1= 0°， j2= 60°， j3= 36°，j5= 0°。f=50 Hz。故障电流信号模型为：

用12位A/D转换器对故障电流信号采样，量化时取到小数点后4位。工频周期采样点数N=48。

分别在无干扰和有干扰信号情况下做仿真实验。无干扰信号的静态仿真结果如表1所示。加入60 dB高斯白噪声[14]后的静态仿真结果如表2所示。

从表1 可看出在 I0/I1分别为 0.2、1、5，t分别为 5 ms、50 ms、100 ms、200 ms 情况下，基波幅值 I1的计算误差一般情况下在 0~0.54%之间，个别情况下误差达到 2.7%。基波相角1j 的计算误差不超过 1º。二次谐波幅值 I2的计算误差一般情况下在0~0.28%之间，个别情况下误差达到 1.5%。三次谐波幅值 I3的计算误差在 0~0.22%之间。五次谐波幅值 I5的计算误差一般情况下在 0~0.15%之间，个别情况下误差达到 1.9%。计算结果表明本文提出的算法在无干扰时具有较高精度。

从表2可看到，在I0/I1分别为0.2、1、5，τ分别为5 ms、50 ms、100 ms、200 ms，加入60 dB高斯白噪声的情况下，基波幅值I1的计算误差有所增加，但是一般情况下误差不大于1%，个别情况下最大误差达到2.48%。基波相角1j的计算误差一般情况下不超过1º，个别情况下最大误差达到-2.649º。二次谐波幅值I2的计算误差一般情况下不超过1%，个别情况下误差达到2.24%。三次谐波幅值I3的计算误差一般情况下不超过1%，个别情况下达到1.78%。五次谐波幅值I5的计算误差一般情况下不超过1%，个别情况下误差达到1.2%。计算结果表明，本文提出算法在存在60 dB高斯白噪声干扰下仍具有较高精度。

快速瞬变脉冲群对微机保护的数据采集系统影响较大，其特点是持续时间不长，一般在10 μs左右[15]。可设置当采样值超过某一设定值时，在中断服务程序内两次启动A/D转换，将后一次得到的采样值作为本次系统的采样值参与本文算法的计算。

随着智能变电站的发展，电子式互感器逐步取代传统的电磁式继电器。电子式互感器在实际应用中受到变电站现场的电磁环境的干扰偶尔会输出异常数据，同时传输设备也有可能在数据传输过程中形成异常数据。针对采样数据中存在异常数据的情况，文献[16]研究了在检测出采样数据异常点后，利用三次样条插值方法对坏点进行插值计算，作为修正后的采样数据。本文也采取这种异常数据的纠正方法。

为验证含有异常数据情况下本算法的有效性，假设一个周期的第2个采样数据为异常数据，计算结果表明，基波的幅值 I1误差一般不超过 1%，个别点误差达到 2.22%，基波相角 φ1的计算误差一般情况下不超过 1º。它表明了本文算法的有效性。

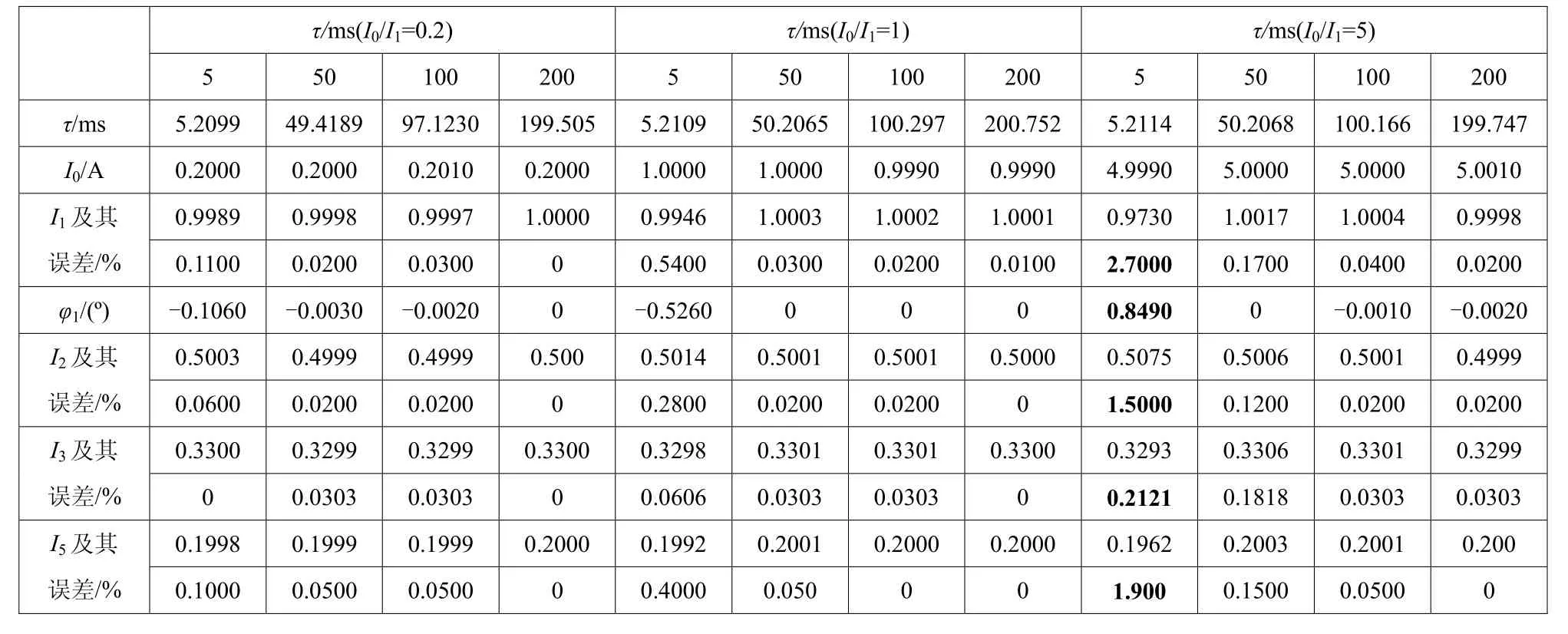
表1 φ1=0º、I1=1.0 A 下采样信号中无干扰信号的静态仿真结果Table 1 Static simulation results of interference-free signal sampled signal when φ1=0º, I1=1.0 A

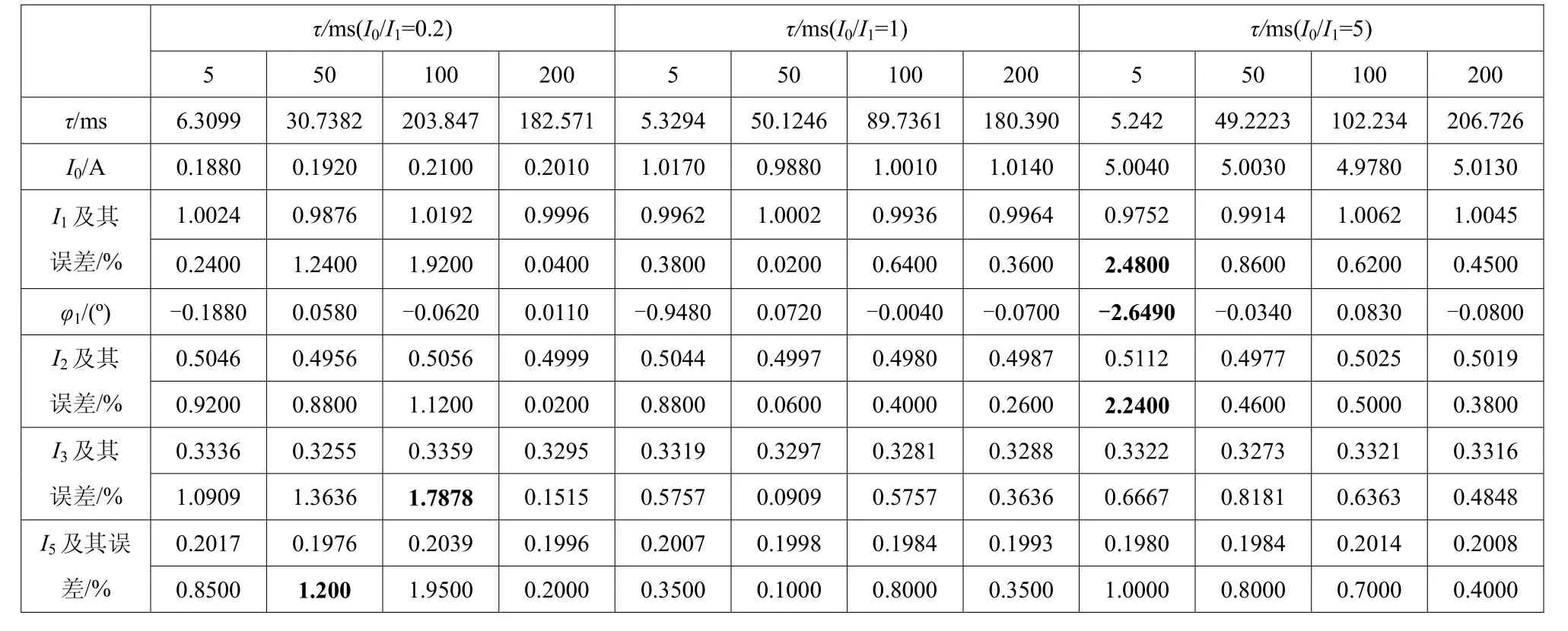
表2 φ1=0º，I1=1.0 A 下采样信号中存在 60 dB 高斯白噪声的静态仿真结果Table 2 Static simulation results with 60 dB white Gaussian noise signal in sampled signal when φ1=0º, I1=1.0 A

3.2 动态算例分析与验证

为验证本算法在距离保护中应用的有效性，利用PSCAD软件，参照文献[17]所用京津唐500 kV超高压输电线路，按照分布参数建立一条300 km长的线路，仿真模型如图1所示。

图1 仿真模型Fig. 1 Simulation model

线路参数如下：r1=0.020 83 Ω/km；l1=0.894 8 mH/km； c1=0.012 9 μF/km ； r0=0.114 8 Ω/km； l0= 2.288 6 mH/km；c1=0.005 23 μF/km。M侧系统参数：EM=525∠0° V；RM1=1.051 5 Ω；LM1=0.137 3 H；RM0= 0.6 Ω ； LM0=0.092 6 H 。 N 侧系统参数： EN= 525∠-30º V；RN1=26 Ω；LN1=0.142 98 H；RN0=20 Ω；LN0=0.119 27 H。

分别设置系统在不同情况下发生故障对所提算法进行验证，故障发生在0.2 s，故障保持时间为1 s。

设置系统发生单相接地故障，故障位置分别在线路 MN 的 10%、50%、90%处，过渡电阻分别为0.01 Ω、10 Ω、100 Ω、300 Ω。分别利用精确的对数函数和简化方法(取式(18)的前两项)计算t，分别利用精确的指数函数和近似方法(取泰勒展开式的前 10 项)计算基波幅值 I1和基波相角 φ1。动态仿真实验的结果如附表1~附表3 所示。

设置系统在线路MN的10%处发生单相接地故障，过渡电阻为10 Ω。利用本文算法、传统全波傅氏算法和文献[6]的算法，分别对故障电流进行处理，三种算法计算得到的基波分量如图2所示。

图2 线路MN的10%处发生单相接地故障，过渡电阻为10 Ω的仿真结果Fig. 2 Simulation results of the single-phase ground fault with location at 10% of line MN and 10 Ω transition resistance

由图2分析当故障电流包含衰减直流分量时，本文提出的算法能进行有效滤除，输出值较快接近于稳定值，且误差较小，较文献[6]算法在精度上更优。

分别设置系统在线路MN的70%、90%处发生单相金属性接地故障，分别将本文提出算法、传统全波傅氏算法运用于距离保护阻抗计算。在线路MN的70%处，故障发生在距离I段保护范围之内，在线路MN的90%处，故障发生在距离保护I段范围之外。两种故障情形下的阻抗计算结果分别如图3、图4所示。阻抗计算值的轨迹变化方向如图3、图4中箭头所示，其右上角为阻抗计算值轨迹的局部放大图。图3表明，传统傅氏算法的阻抗计算值趋于稳定的速度慢，并且较靠近保护定值边界、容易发生拒动。本文算法在故障过程中的阻抗计算值能够快速趋于稳定值，并且离保护动作边界稍远。

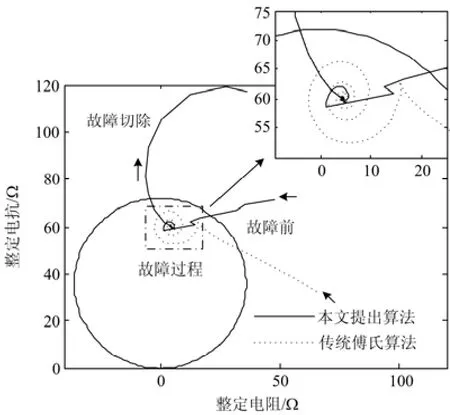
图3 在线路MN的70%处单相金属性接地故障阻抗计算值轨迹图Fig. 3 Impedance calculated trajectories of the single phase ground fault with location at 70% of the line MN

图4 在线路MN的90%处单相金属性接地故障阻抗计算值轨迹图Fig. 4 Impedance calculated trajectories of the single phase ground fault with location at 90% of the line MN

图4 表明，传统傅氏算法的阻抗计算值轨迹在故障发生的初期进入保护整定圆内，此时保护有可能发生误动。而本文算法的阻抗计算值从开始到稳定一直处于保护动作范围之外，且离保护定值边界稍远，保证了距离I段保护能够可靠不动作。

3.3 结果分析

附表4、附表5分别给出了145j =o、I1=1.0 A下无干扰信号和加入60 dB高斯白噪声信号后的静态仿真结果。无干扰信号情况下，基波幅值I1的误差为0~0.8%，基波相角φ1的计算误差不大于0.5º。二次谐波幅值I2的计算误差一般情况下在0~0.3%，个别情况下误差达到1.52%。三次谐波幅值I3的计算误差一般情况下在0~0.3%，个别情况下误差达到1.52%。五次谐波幅值I5的计算误差一般情况下在0~0.4%，个别情况下误差达到1.9%。附表4计算结果表明本文提出算法在无干扰时具有较高精度。

在有干扰信号情况下，基波幅值I1的误差在一般情况下不大于1%，个别情况下最大误差达到2.1%。基波相角φ1的计算误差不大于0.8º。二次谐波幅值I2的计算误差一般情况下不超过1%，个别情况下误差达到2.24%。三次谐波幅值I3的计算误差一般情况下不超过1%，个别情况下误差达到1.79%。五次谐波幅值I5的计算误差一般情况下不超过1%，个别情况下误差达到1.95%。从附表5可看出，在有干扰信号存在时，有的情形下t的计算误差较大，但是I0、基波幅值和相角的计算结果仍较为准确，说明本算法在静态算例下有较强抗干扰能力。

附表1~附表3分别给出在不同故障位置和过渡电阻下的动态仿真实验结果。从附表1~表3可看出，采用简化计算 τ的方法，给 I1的计算带来误差一般不超过 0.5%，最大为 0.68%；给 φ1的计算带来误差一般不超过 1%，最大为 2.73%。

从公式(22)可看到，基波分量的幅值和相角计算与衰减直流分量的 I0和 τ有关。本文中直流衰减分量的 I0计算误差取决于 A/D 转换的量化精度和采样信号的准确度，不受τ计算误差的影响。

τ 的计算误差主要由式(18)中取泰勒展开式前两项的截断误差和干扰信号造成。由式(19)近似计算的衰减直流分量τ在一般情况下较准确。但是当τ 的真实值很小或者过渡电阻较大造成 τ较小时，其近似计算误差较大。

I1的误差由 I0的计算误差、利用式(22)计算衰减直流分量的截断误差及干扰信号等造成，主要与I0的计算误差有关，τ的计算误差对精确估算基波分量的影响较小[6]。即使当 τ的计算存在误差(过渡电阻很大、τ较小时)，本算法的基波分量幅值和相角的计算仍很准确。不同故障位置和过渡电阻的实验表明，采用本文的滤除衰减直流分量方法及其简化计算，能够获得较为准确的基波分量幅值和相角。

当在线路MN末端发生单相接地故障、过渡电阻很大(300 Ω)时，虽然 τ很小，其计算误差较大，但是由于此时 I0的值较小，即直流衰减分量很小且衰减很快，对基波分量计算的影响较小。

4 结论

本文提出了一种新型滤除衰减直流分量的全波傅氏改进算法。利用一个周期内采样值序列估算出衰减直流分量的时间常数与初始值，因此在故障发生后采样点数为N时，利用全波傅氏改进算法就能得到基波分量的准确值，不需要在一个周波采样

数据之外额外增加采样点，达到了保护快速动作的目的。多组静态和动态算例表明了本文算法的有效性，能够有效地消除衰减直流分量，显著地减小衰减直流分量对基波分量计算的影响，并实现了工程应用的近似简化计算，本文算法实现简单、计算量小、准确性高，有利于工程应用。

感谢国网四川省电力公司科学技术项目“新一代智能变电站全数字可视化仿真培训系统研究”支持。

附录

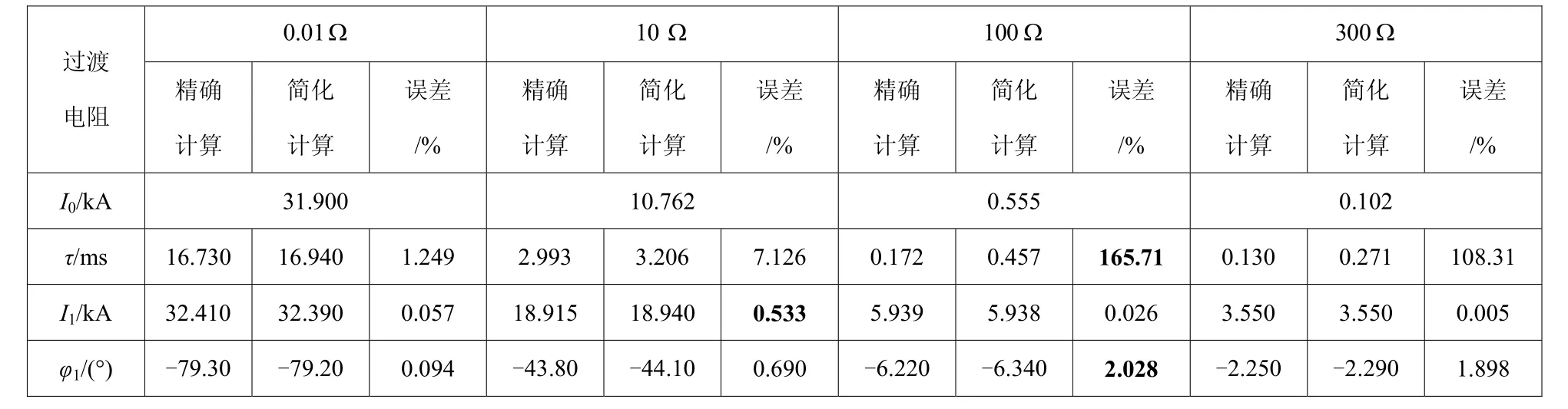
附表1 线路 MN 的 10%处发生单相接地故障计算结果Table 1 The results of single phase ground fault with location at 10% of the line MN

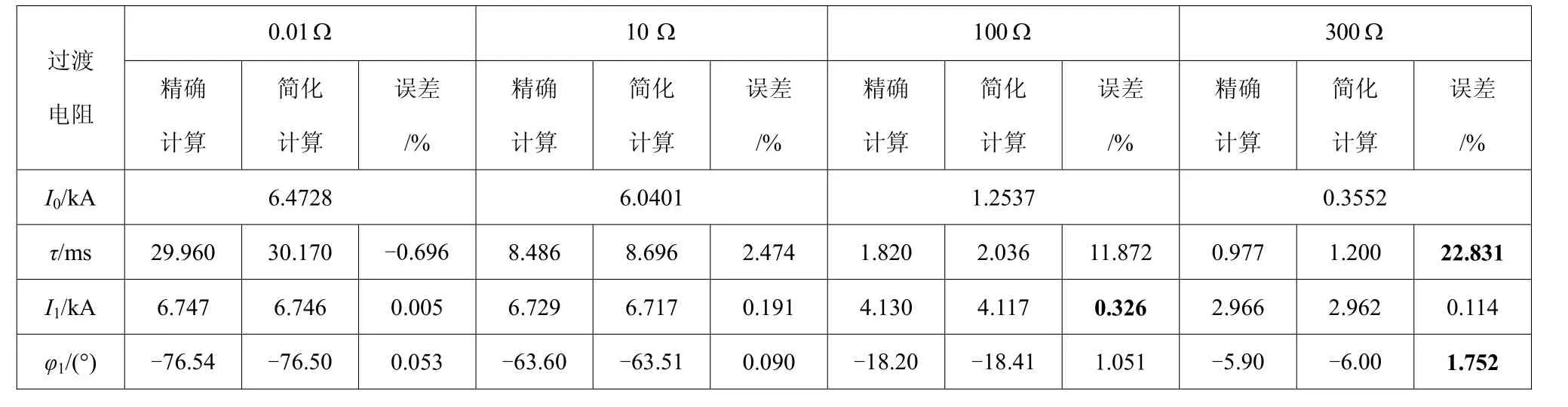
附表2 线路 MN 的 50%处发生单相接地故障计算结果Table 2 The results of single phase ground fault with location at 50% of the line MN

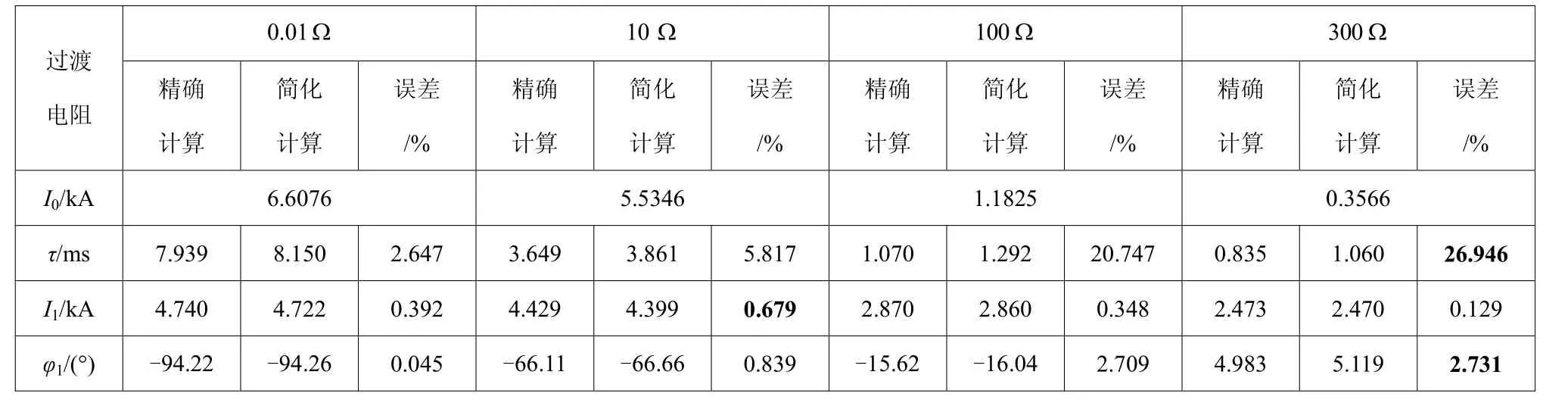
附表3 线路 MN 的 90%处发生单相接地故障计算结果Table 3 The results of single phase ground fault with location at 90% of the line MN

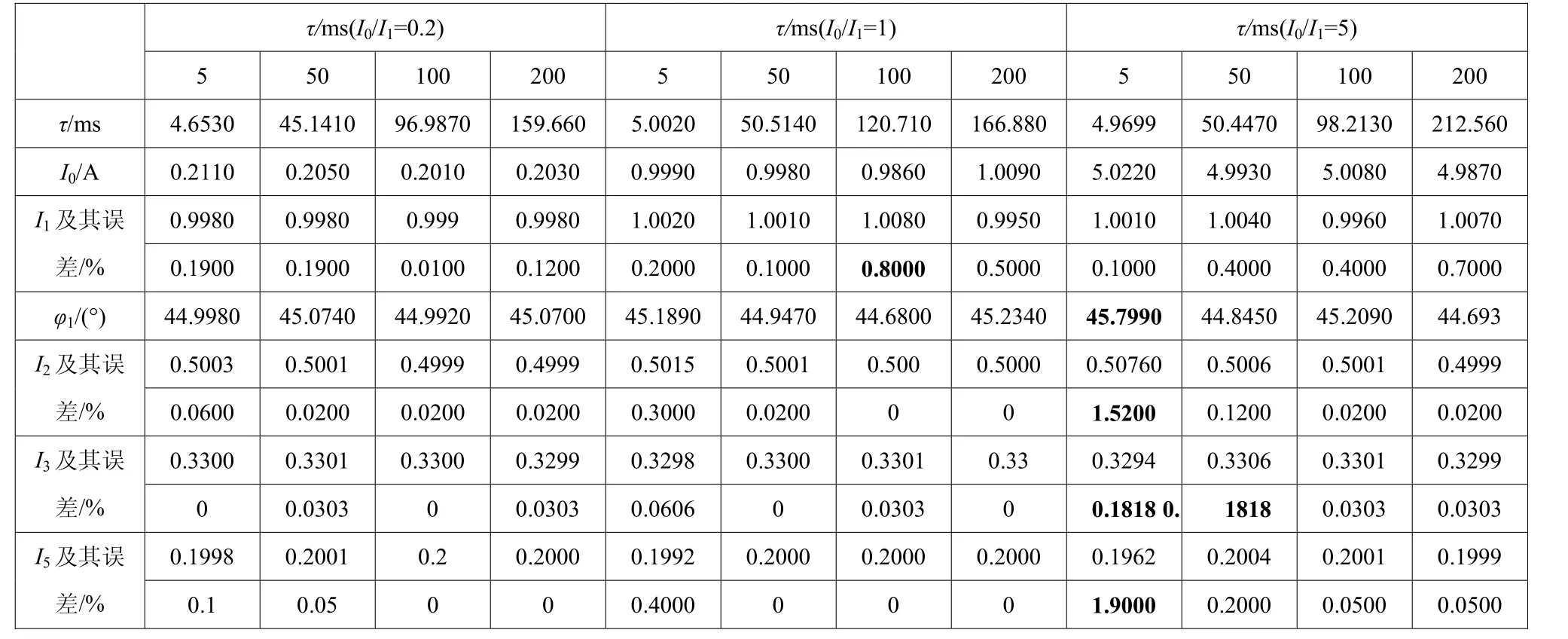
附表4 φ1=45º、I1=1.0 A 下采样信号中无干扰信号的静态仿真结果Table 4 Static simulation results of interference-free signal sampled signal at φ1=45º, I1=1.0 A

附表5 φ1=45º、I1=1.0 A 下采样信号中存在 60 dB 高斯白噪声的静态仿真结果Table 5 Static simulation results with 60 dB white Gaussian noise signal in sampled signal at φ1=45º, I1=1.0 A

[1]陈奎, 孙常青, 张丽, 等. 一种新方法在监视线保护中的应用[J]. 电力系统保护与控制, 2010, 38(6): 76-83. CHEN Kui, SUN Changqing, ZHANG Li, et al. Application of a new method in the cable monitor wire protection[J]. Power System Protection and Control, 2010, 38(6): 76-83.

[2]吕思颖, 裴旵 , 秦昕, 等 . 基于小波多尺度分析和Kalman 滤波的微机保护算法[J]. 电力系统保护与控制, 2015, 43(21): 54-59. LÜ Siying, PEI Chan, QIN Xin, et al. Microprocessorbased protection algorithm based on wavelet multi-scale analysis and Kalman filter[J]. Power System Protection and Control, 2015, 43(21): 54-59.

[3]雷乃清, 许钰婷. 基于小波分析的电动机综合保护器设计[J]. 电力系统保护与控制, 2015, 43(12): 129-133. LEI Naiqing, XU Yuting. Design of motor comprehensive protector based on wavelet analysis[J]. Power System Protection and Control, 2015, 43(12): 129-133.

[4]ALAM A S. A new fast algorithm to estimate real-time phasors using adaptive signal processing[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 807-815.

[5]HOOSHYAR A, SANAYE-PASAND M. Accurate measurement of fault currents contaminated with decaying DC offset and CT saturation[J]. IEEE Transactions onPower Delivery, 2012, 27(2): 773-783.

[6]张小鸣, 费雨胜. 一种滤除衰减直流分量的电流估计新算法[J]. 电力系统保护与控制, 2010, 38(20): 90-95. ZHANG Xiaoming, FEI Yusheng. A new current estimation algorithm to filter decaying DC component[J]. Power System Protection and Control, 2010, 38(20): 90-95.

[7]刘辉乐, 陈皓, 黄志华. 一种消除非周期分量的牛顿递推采样值修正法[J]. 继电器, 2004, 32(17): 28-30. LIU Huile, CHEN Hao, HUANG Zhihua. An improved Newton iterative algorithm to eliminate non-period components from sampling data[J]. Relay, 2004, 32(17): 28-30.

[8]CHO Y S, LEE C K, JANG G, et al. An innovative decaying DC component estimation algorithm for digital relaying[J]. IEEE Transactions on Power Delivery, 2009, 24(1): 73-78.

[9]厉伟, 陈刚. 一种利用 LabVIEW 滤除衰减直流分量的改进算法[J]. 电力系统保护与控制, 2014, 42(11): 7-12. LI Wei, CHEN Gang. An improved algorithm to filter delaying DC component based on LabVIEW[J]. Power System Protection and Control, 2014, 42(11): 7-12.

[10]李晨, 张杭, 张爱民, 等. 一种能滤除衰减直流分量的新递推离散傅氏算法[J]. 继电器, 2005, 33(17): 17-20. LI Chen, ZHANG Hang, ZHANG Aimin, et al. A recursive discrete Fourier algorithm for filtering decaying DC component[J]. Relay, 2005, 33(17): 17-20.

[11]幸晋渝, 刘念, 郝江涛, 等. 故障电流中衰减直流分量的滤波算法研究[J]. 继电器, 2005, 33(13): 10-12. XING Jinyu, LIU Nian, HAO Jiangtao, et al. Research of decaying DC removal algorithms in fault current[J]. Relay, 2005, 33(13): 10-12.

[12]黄世年, 佟为明, 郭志忠, 等. 直接提取基频分量瞬时值的快速滤波算法[J]. 电力系统保护与控制, 2013, 41(3): 44-49. HUANG Shinian, TONG Weiming, GUO Zhizhong, et al. A fast filtering algorithm for extracting fundamental instantaneous value[J]. Power System Protection and Control, 2013, 41(3): 44-49.

[13]张秋丽, 黄纯, 贺建辉, 等. 一种消除衰减直流分量影响的改进 DFT 递推算法[J]. 电力系统保护与控制, 2010, 38(24): 1-5. ZHANG Qiuli, HUANG Chun, HE Jianhui, et al. An improved recursive discrete Fourier transform algorithm for eliminating decaying DC component[J]. Power System Protection and Control, 2010, 38(24): 1-5.

[14]SIDHU T S. Accurate measurement of power system frequency using a digital signal processing technique[J]. IEEE Transactions on Instrumentation and measurement, 1999, 48(1): 75-81.

[15]程利军, 李轶群, 焦韶华. 快速瞬变脉冲群对微机保护装置数据采集系统的影响及对策[J]. 电力自动化设备, 2004, 24(1): 14-19. CHENG Lijun, LI Yiqun, JIAO Shaohua. Influence of EFT on data acquisition system of numerical protection and its countermeasure[J]. Electric Power Automation Equipment, 2004, 24(1): 14-19.

[16]董义华, 孙同景, 徐丙垠. 基于三次样条插值理论的电子式互感器数据同步[J]. 电力自动化设备, 2012, 32(5): 102-107. DONG Yihua, SUN Tongjing, XU Bingyin. Data synchronization based on cubic spline interpolation for electronic instrument transformers[J]. Electric Power Automation Equipment, 2012, 32(5): 102-107.

[17]索南加乐, 何方明, 焦在滨, 等. 工频变化量距离元件特性的研究 [J]. 中国电机工程学报 , 2010, 30(28): 59-65. SUONAN Jiale, HE Fangming, JIAO Zaibin, et al. Research on the characteristics of distance element based on the power-frequency voltage and current variation[J]. Proceedings of the CSEE, 2010, 30(28): 59-65.

(编辑周金梅)

A full-wave Fourier improved algorithm of filtering decaying DC component

WU Jiwei1, TONG Xiaoyang1, LIAO Xiaojun2, ZHENG Yongkang3, HUANG Zhongsheng2, LIU Tao3, HAN Huarong2
(1. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. State Grid Sichuan Electric Power Company Skills Training Center, Chengdu 610072, China; 3. State Grid Sichuan Electric Power Research Institute, Chengdu 610072, China)

Full-wave Fourier algorithm is influenced by the decaying DC component when extracting fundamental component from the fault current. In order to solve the problem, a novel full-wave Fourier algorithm of filtering decaying DC component is proposed and the derivation of the decaying DC component parameters calculation is given. Firstly, the initial amplitude and decay time constant of the decaying DC component can be calculated with the sampling values in one cycle of the fault current, and then the corrected sample values can be got by using the sampling values minus the decaying DC component. The fundamental component can be got by the revised sampling values with full-wave Fourier improved algorithm. The static model simulation signals and PSCAD/EMTDC simulated signals are applied to test the performance of the algorithm separately. The simulation results illustrate that the proposed algorithm can effectively reduce the impact of decaying DC component. Compared with traditional algorithms, the proposed algorithm only needs one cycle of sampling data. The fundamental component is calculated accurately with a small amount of calculation.

decaying DC component; parameter calculation; time constant; full-wave Fourier algorithm; fundamental component

TM71

1674-3415(2016)02-0009-09

2015-04-09；

2015-05-18

吴继维(1990-)，男，硕士研究生，研究方向为微机继电保护仿真；E-mail: 896250021@qq.com

童晓阳(1970-)，男，通信作者，博士，副教授，研究方向为电网故障诊断、变电站自动化、广域后备保护；E-mail: xytong@swjtu.cn

廖小君(1973-)，男，硕士，副教授，研究方向是继电保护、智能变电站自动化。