AES算法的研究与其密钥扩展算法改进

刘艳萍，李秋慧（河北工业大学电子信息工程学院，天津　300401）



AES算法的研究与其密钥扩展算法改进

刘艳萍，李秋慧
（河北工业大学电子信息工程学院，天津300401）

摘要：种子密钥是高级加密标准（AES）的关键参量，而密钥扩展算法则是保护种子密钥不被盗取的重要实现方法。首先对加密算法的实现方法与过程进行研究，然后详细分析密钥扩展算法的运算过程，最后针对原有算法存在的安全隐患和破解难度不高的缺点，通过循环移位对密钥扩展算法进行改进，提出一种具有“运算方向单一性”的密钥扩展实现策略；并在Keil环境、12 MHz条件下测试各算法。通过实验结果分析得到，在保证运算速率的前提下，这种新算法可以进一步改善AES算法中种子密钥的安全性，并且没有破坏与加密算法间的同步特性。

关键词：高级加密标准；密钥扩展算法；种子密钥；循环移位

0　引　言

AES（Advanced Encryption Standard）加密算法的原型是由比利时密码学家Joan Daemen和Vincent Rijmen设计的Rijndael加密算法。AES作为目前安全性最高标准[1]，已在信息安全领域得到广泛的应用。AES算法是分组密码[2]设计的一种很好的实现方式，分组密码设计是指存在一个算法，可以在密钥的控制下简单而迅速地从一个置换子集中（足够大且足够好）选出一个置换，对当前输入的明文进行加密交换。Rijndael加密算法设计具有简单性、高效性、对称性、模块性等优点，但是通过研究目前对算法的攻击方法发现，AES采用了扩充种子密钥生成子密钥的方式，密钥扩展算法设计的比较简单，所以具有高效、快速等优点。而能量攻击[3]和渗透攻击等攻击正是在AES算法中的密钥扩展算法中做文章，来攻击AES加密算法的安全性。此算法在攻击者获得一轮子密钥，就可以推导出原种子密钥的缺陷。逆推过程是密钥破解者主要的思维方式，那么如果能够找到一种方法可以使算法的运算方向具有单一性，即算法只可以从前往后计算而不可以从后往前推算，就可以防范攻击了。在设计密钥扩展算法时要遵循的准则包括以下几方面：

（1）简单性，每一次加密都要进行10轮的密钥扩展，如若算法比较复杂，会影响加密的效率；

（2）即时性，加密过程的每一轮运算都离不开轮密钥，无需等到所得的密钥全部生成再进行加密运算，加密与密钥扩展二者可以同时进行。

1　AES加密算法研究

有限域[4]通俗的定义就是函数的运算结果全部都在一个域中，与熟悉的实数域不同，在有限域中规定一个最大的值，例如有限域GF（28）这个域的最大值是256，其他所有超过这个最大值的数都会通过一定的方法使其回归到不超过最大值的这个域中。有限域的概念在密码学中被广泛应用，而有限域的乘法运算更是AES算法实现的数学基础，在下面将会对有限域的乘法逆运算进行叙述。

AES算法的实现过程主要包括两大部分，加密过程和密钥扩展，其是一个数据块和密钥块均可变的迭代分组加密算法，有三种分组长度128位，192位，256位，下面以128位为例介绍算法的加密过程。

AES的明文分组（即各轮的输入与输出以及每一次变换所产生的中间量）称之为状态，所有的运算均是以状态为单位进行的。如图1所示，加密部分主要分为四个步骤：S盒变换（作用在状态中每个字节上的一种非线性字节转换，可以通过计算出来的S盒进行映射）、行变换、列变换、轮密钥加。

图1　128位数据分组加密过程

1.1S盒变换

作为算法实现过程中惟一一个非线性部件，S盒变换的作用是实现混淆功能。AES采用的S盒是由限域GF（28）下以模m(x)=x8+ x4+ x3+ x + 1的乘法逆运算和GF（2）下的仿射变换[5]实现的，选取的S盒具有最佳的线性偏差和差分均匀性。

（1）有限域GF（28）中的乘法逆运算

若ω∈GF（28），存在ω的逆元素X，则X表示为：

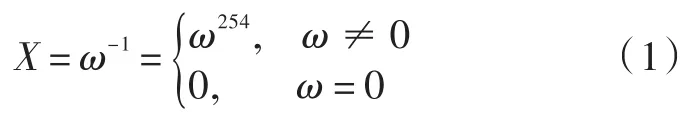
其中‘00’就是其本身。

（2）GF（2）下的仿射变换

假设X在GF（28）中的元素分量表示为（X7，X6，X5，X4，X3，X2，X1，X0），变换如下：

1.2行变换

行变换（Shiftrows）的实质就是字节的换位，它将状态中的各行按照不同的偏移量进行循环移位，如图2所示，状态中第1行不做任何变换，第2行做1 B的循环左移，第3行做2 B的循环左移，第4行做3 B的循环左移。状态是一个128 b的分组数组，行变换是将一个字节从一列移到另一列，实际字节移动的线性距离最小的也是4 B。

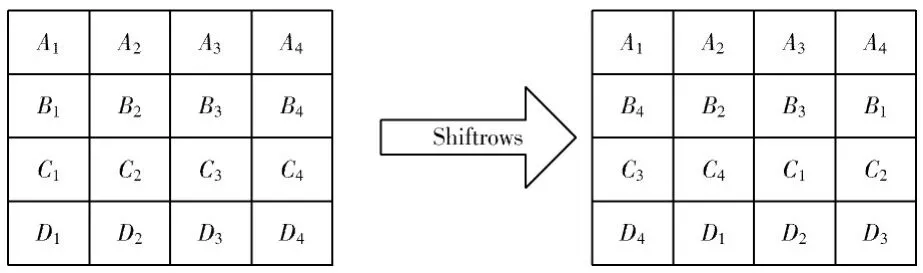
图2　行变换移位图

1.3列变换

列变换的操作对象是状态的各列，列中的每个字节通过一种映射关系得到一个新的字节，如式（3）所示，其加、乘运算都是基于有限域GF（28），使得每列字得到充分的混淆。

在此变换中的乘法运算是有限域GF（28）的乘法，它为模GF（2）域的一个8次不可约多项式乘法，表示为，这个不可约多项式为m(x) = x8+ x4+ x3+ x + 1。若c(x) = a(x)b(x)，则c(x) = a(x) *b(x) mod m(x)。

将式（3）写成：

S0，m′={02 }16S0，m+{03 }16S1，m+{01 }16S2，m+{01 }16S3，m

S1，m′={01 }16S0，m+{02 }16S1，m+{03 }16S2，m+{01 }16S3，m

S2，m′={01 }16S0，m+{01 }16S1，m+{02 }16S2，m+{03 }16S3，m

S3，m′={03 }16S0，m+{01 }16S1，m+{01 }16S2，m+{02 }16S3，m

例如：{02}16×{54}16={A8}16，{02}16写成GF（28）域的多项式为x，{54}16写成GF（28）域的多项式为x6+ x4+ x2，有：

1.4轮密钥加

轮密钥加运算就是每轮的状态与对应的128 b的轮密钥的异或运算。由此可以看出轮密钥扩展的复杂度直接影响着算法的安全性。下面就针对密钥扩展算法进行详细分析。

2　密钥扩展算法分析与改进

2.1AES原密钥扩展算法

AES加密算法密钥扩展的实现是直接采用把种子密钥直接扩充的方式，其是面向字节的，这样使得算法实现具有较高的效率。128 b的加密要进行10轮的运算，再加上最初的种子密钥，一次完整的加密过程需要11个分组，若以列为单位则最终的密钥总长度为44字。密钥扩展的过程如图3所示，由Wi-4Wi-3Wi-2Wi-1计算出WiWi+1Wi+2Wi+3首先是Wi-1进行RotByte移位变换由W[0][i-1]W[1][i-1]W[2][i-1]W[3][i-1]变为W[1][i-1]W[2][i-1]W[3][i-1]W[0][i-1]，变换后的数列进行一次SubWord变换，最后再与Wi-4和轮常量Rcon[]进行异或运算得到Wi，Rcon[]=（RC[i]，00，00，00），均为16进制，其中i表示轮数，RC[i]的值如表1所示。其中，SubWord变换是非线性运算，将输入的每个字节替换成S盒中对应的值；RotByte变换是一个移位运算，它将输入的一个4 B的字进行了1 B的循环移位，例如输入（A0，A1，A2，A3）经RotByte变换得到（A1，A2，A3，A0）。

图3　密钥扩展算法实现过程

表1　轮常量RC[i]值表

如图3所示，子密钥后三个字由本轮密钥的前一个字与上一轮密钥得到，即Wi与Wi-3异或得到Wi+1，Wi+1与Wi-2异或得到Wi+2，Wi+2与Wi-1异或得到Wi+3。

由此，最后得到的扩展密钥是一个直线阵列，最初的前4 B由种子密钥填充，其他字节以4 B为一个单位字，由前4 B按照这种递归算法生成后面的4字。

从密钥扩展的实现过程得知，虽然每轮都进行一次复杂化的运算，但是每轮密钥与它的上轮密钥有着较强的相关性。假设攻击者获取某一轮子密钥，那么只需要猜测232次便可以利用已知子密钥推导出其上一轮的子密钥，以致可以推导出包括种子密钥在内的所有轮密钥。需要截获4轮之后的轮密钥穷尽次数达到2128次，此时才能达到暴力破解的强度，这正好给能量攻击和渗透攻击破解算法带来了突破口。所以在此希望可以找到一种方式既可以保留原密钥扩展算法的高效性，又可以尽可能提高算法的单向性，使得算法的逆推不可实现。

2.2密钥扩展算法的改进

文献[6]中对算法的改进借助其他算法的运算方式而且提高了每轮运算的复杂度，这使得原本算法的优点不复存在。在保留AES原始密钥扩展算法的优势的基础上，本文针对其不足之处，从提高攻击强度并兼顾算法执行效率方面进行改进，提出了以下几种改进方法。

方法一：AES算法原始密钥扩展算法本身有着简单、灵活等优点，所以在原算法的基础上进行改进是最理想的。由原算法分析可知，其最大的缺点就是轮密钥间的相关性很强，为了避免这种不足，将密钥的每个字都经过一轮复杂化运算，保持原密钥扩展算法中复杂化运算[7]的轮常量Rcon[]的定义，RotByte变换和SubWord变换的运算规则不变，如图4所示，然后经过复杂化运算获得字与未复杂化的字异或后得到下一轮密钥的一个字，直接对种子密钥进行扩展。这种改进的密钥扩展方法可以使得轮密钥间的相关性减小，具有运算方向的单一性，即数据只可从前往后运算，不可从后向前推导，即使是第一轮子密钥被截获，由此推导种子密钥也许要尝试2128次，可以达到暴力破解的强度，安全性与原算法相比得到了大大的提高。

方法二：在改进方法一中虽然安全强度得到了提高，但是每轮子密钥的生成都要经过4次复杂化的运算，这使得算法的运算效率与原算法相比降低了很多。而原算法最大的弊端就是相邻两轮间的相关性较大，为了减小原算法中相邻两轮密钥间的相关性[8]，方法二在原来的基础上做出如下改进：

保留原密钥扩展算法的复杂化运算的各个步骤：移位变换（RotByte）、SubWord变换、轮常量Rcon[]异或运算，和基本操作流程不变，在种子密钥上进行直接扩展，密钥扩展改进算法的过程如图5所示，同样由Wi-4Wi-3Wi-2Wi-1计算出WiWi+1Wi+2Wi+3，依然是由Wi-4Wi-1经过复杂运算得到Wi，由Wi-3和Wi-2异或得到Wi+1，后2个字不再采取依靠上轮子密钥的方式获取，而是由已生成的本轮密钥的前2个字，Wi，Wi+1异或得到Wi+2；Wi+1，Wi+2异或得到Wi+3。

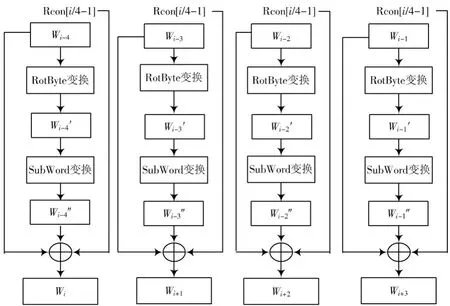
图4　改进方法一密钥扩展算法实现过程

图5　改进方法二密钥扩展算法实现过程

从改进算法的实现过程可以看出，与原算法相比生成的子密钥与上一轮的密钥的相关性大大减小了，推导出一轮子密钥需要猜测次数由原来的232次增加264次，即使攻击者得到一轮子密钥，对上轮子密钥的推导也毫无意义，改进算法已经具有了运算方向单一的特性。虽然这种改进降低了每轮之间的相关性，但是每轮内部的相关性却增加了，只要将每轮的前2个字猜测出来，后2个字可直接获得，这也使得算法的安全性受到一定程度上的威胁。

方法三：改进方法二中Wi+2是借助Wi，Wi+1；Wi+3借助Wi+1，Wi+2；由此可以得出Wi+2是一个关键参量，只要破坏其平衡就可以降低每轮内部的相关性。若在全部密钥生成之后对其进行换位操作会降低算法的即时性，影响效率，所以给每轮子密钥的Wi+2字进行1次循环移位[9]，如图6所示，从生成的子密钥的第2轮开始将每轮密钥的第3个字与前一轮的第3个字交换，将交换后的分组数作为最终的子密钥。这样可以将10轮子密钥紧密联系起来，即使猜测出一轮子密钥的前2个字，也无法推导出第3、第4个字，若要想获得一轮子密钥，必须将10轮密钥的前两个字都猜测出来。而就一轮而言则需要穷举2128次，这完全能与暴力破解的强度相媲美。

图6　改进方法三算法数据位置变换关系

3　实验结果分析

用C语言实现原密钥扩展算法和改进后的密钥扩展算法，在Keil环境中模拟12 MHz时测试三种改进算法的运行效率并与原算法进行对比，其安全强度和效率如表2所示。

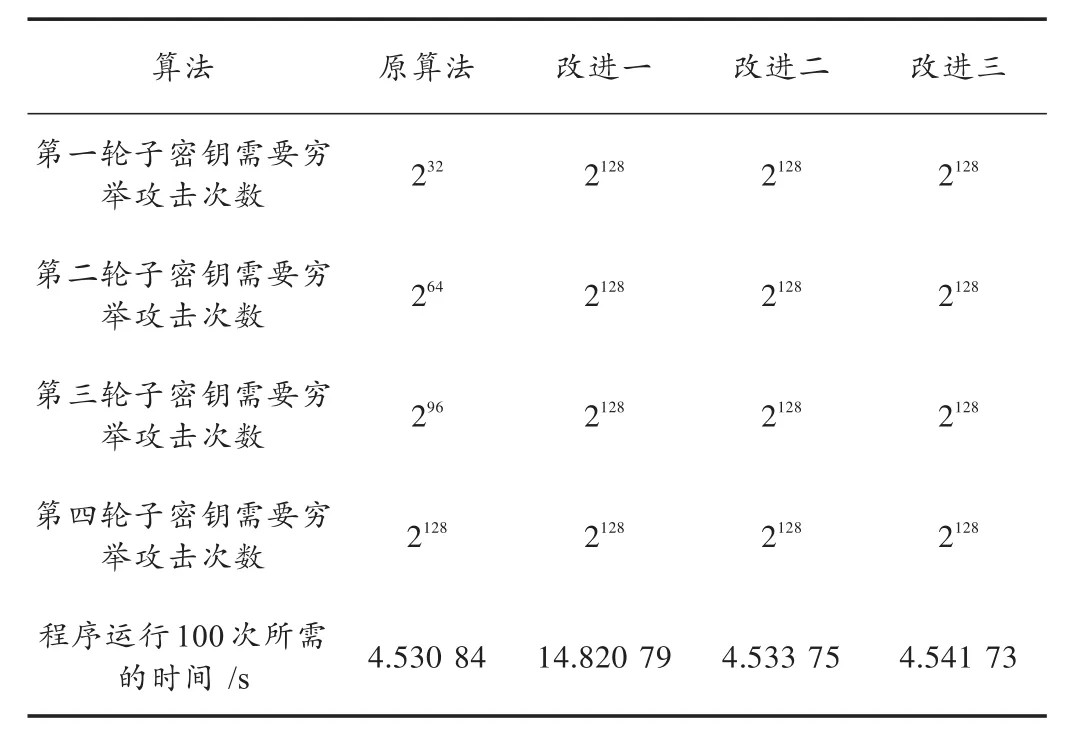
表2　改进算法与原算法对比表

三种改进算法都在一定程度上提高了算法本身的安全性。方法一虽然安全强度增强，但是运算效率明显降低；方法二在没有影响效率的前提下很好地提高了密钥的安全性，而其子密钥内部的相关性却很高，子密钥的安全性降低，在某种程度上也会影响加密算法的安全性；在此基础上方法三采用了外轮循环移位的方法很好的解决了方法二中存在的不足，而且也保证了密钥的安全强度和运算速率，不会在原算法的基础上增加任何额外的负担，具有了更强的抗攻击性，同时也很好地保留了密钥生成过程与加密过程的同步性。

4　结　语

本文对AES算法的实现过程进行了详细的研究与分析，包括S盒变换、行变换、列变换、轮密钥加和与密钥运算的轮换顺序。并针对AES原密钥扩展算法的缺陷，在其基础上进行改进，提出了三种新的密钥扩展算法，并对其三者进行了对比分析。AES加密算法本身拥有众多的优良的特性，进一步地深入研究对现代信息安全的保护具有重大的意义。

参考文献

[1]郎荣玲，夏煜，戴冠中.高级加密标准（AES）算法的研究[J].小型微型计算机系统，2003，24（5）：905⁃908.

[2]杜钦生，王美琴，曹宝香.Rijndael加密算法的密钥扩展算法的研究[J].信息技术与信息化，2005（5）：49⁃52.

[3]吴文玲，贺也平.Mars和Rijndael的能量攻击[J].软件学报，2002，13（4）：532⁃536.

[4]林志华.Rijndael算法的研究与分析[D].西安：西安电子科技大学，2004.

[5]孙爱娟.基于AES加密算法的改进及其Matlab实现[D].哈尔滨：哈尔滨理工大学，2009.

[6]王莹，何大军.AES加密算法的改进与实现[J].电脑编程技巧与维护，2010（17）：84⁃86.

[7]杨小东，王毅.AES密钥扩展新方法[J].微电子与计算机，2012，29（1）：102⁃104.

[8]刘博超.基于不可推导性的AES密钥生成算法[D].长春：吉林大学，2011.

[9]多磊，李超，赵惠文.循环移位对Rijndael密码安全性的影响[J].通信学报，2003，24（9）：153⁃161.

Analysis of AES algorithm and its key extension algorithm improvement

LIU Yanping，LI Qiuhui
（School of Electronic Information Engineering，Hebei University of Technology，Tianjin 300401，China）

Abstract：Seed key is the key parameter of Advanced Encryption Standard（AES），however the key extension algorithm is the important realization method for protecting the seed key from being stolen. In this article，the implementation method and process of the encryption algorithm are studied，and the operation process of the key expansion algorithm is analyzed in detail. In view of the shortcomings that hidden trouble in security and low breaking difficulty of the original algorithm，the key expan⁃sion algorithm was improved by means of the cyclic shift，and a new key expansion strategy with single operation direction was designed. Each algorithm was tested under the condition of 12 MHz and in KEIL. The experimental result and analysis show that，under the premise of guaranteeing the operation rate，the new algorithm can further enhance the seed key safety of AES al⁃gorithm，and doesn’t damage the synchronization feature between the encryption algorithm and key expansion algorithm.

Keywords：advanced encryption standard；key extension algorithm；seed key；cyclic shift

中图分类号：TN915.08⁃34；TP391

文献标识码：A

文章编号：1004⁃373X（2016）10⁃0005⁃04

doi：10.16652/j.issn.1004⁃373x.2016.10.002

收稿日期：2015⁃09⁃25

基金项目：国家“863”计划项目（2007aa05z23）

作者简介：刘艳萍（1966—），女，河北秦皇岛人，教授，博士。主要研究方向为DSP技术及FPGA技术。李秋慧（1990—），女，在读硕士研究生。主要研究方向为电子信息技术与工程。