基于TFI的局部网格变形方法研究
2016-06-23杨维龙杨永
杨维龙,杨永
(西北工业大学 航空学院,西安 710072)
基于TFI的局部网格变形方法研究
杨维龙,杨永
(西北工业大学 航空学院,西安710072)
摘要:整体网格变形技术对其他网格技术的使用产生影响,难以相互配合来解决复杂的流动问题。发展一套基于TFI(超限插值法)技术的局部网格变形方法,该方法不同于已有的整体网格变形思路,将网格变形控制在有限的区域内,在保证网格质量的同时,不影响其他区域的网格,因此不会对其他动网格方法的使用造成影响。以带后缘襟翼的NACA0012翼型为例,对翼型俯仰振荡耦合襟翼偏转运动的动态流场进行数值模拟,结果表明:计算结果与实验值吻合良好,证明了本文发展的局部网格变形方法的可行性。
关键词:襟翼偏转;网格变形;俯仰振荡;非定常流动;超限插值法
0引言
现代飞机设计对计算流体力学(CFD)的要求越来越高,在数值模拟飞机部件具有相对运动的复杂绕流时,需要合适的动网格技术使数值模拟过程更加高效准确,网格变形技术是经常使用的一种动网格方法。
网格变形技术是在数值模拟的过程中,随着时间的推进,根据物体的运动规律,使用数值方法更新网格。常用的网格变形方法有超限插值法(TFI)[1]和弹簧类推法[2]。TFI方法是一种代数方法,因此网格变形效率很高。虽然该方法能够在一定程度上保证初始网格的质量,但是只适用于结构网格,并且只适用于网格小幅度变形的情况。弹簧类推法能够解决大幅度的变形问题,但是由于需要迭代求解静力平衡方程,因此需要消耗较多的计算时间。
综上所述,相对于弹簧类推法,TFI方法的变形效率高,适应能力强,易于编程,因此该方法得到了广泛的应用和发展。L.Dubuc等[3]基于TFI方法开发了一套网格变形算法,并通过数值模拟Williams翼型襟翼的强迫振荡验证了该方法的可行性。袁先旭[4]在TFI的基础上,提出了加权TFI动网格生成方法,生成了OREX飞船返回舱外形俯仰振荡的结构动网格。张兵等[5]通过引入旋转矢量的思想,提出了一种带旋转修正的弹簧-TFI混合动网格技术,解决了大幅度变形情况下物面附近网格的正交性问题。
对于飞机具有多个部件相对运动的数值模拟,仅使用网格变形方法有时是无法完成的,需要多种动网格方法配合使用。但是,对于多块网格,由于物面运动带来的扰动是在整个流场区域网格中传播的,通常的网格变形程序是将整个求解区域的网格作为变形对象。然而,在网格变形过程中,物面网格的运动对离该物面较远的网格带来的影响较小,甚至可以忽略。若对这部分网格进行网格变形处理,会造成计算机资源的浪费。并且由于整个求解区域的网格都发生变形,也制约了该方法和其他动网格方法的配合使用。例如,当模拟某螺旋桨飞机的螺旋桨旋转和副翼偏转时,可以使用网格变形技术模拟副翼的偏转[6],使用动态面搭接技术模拟螺旋桨的旋转[7]。但是,动态面搭接技术要求搭接面形状保持不变,整体网格变形的策略就会造成搭接面的变形,造成两种方法无法配合使用。
整体网格变形策略会给其他动网格技术的使用带来影响,为了解决该问题,本文首先发展一套基于TFI技术的局部网格变形方法,将网格变形的区域限定在指定的范围内,从而不会影响变形域外的网格;其次对NACA0012翼型俯仰振荡耦合襟翼偏转运动的动态流场进行数值模拟。
1网格变形方法
1.1局部网格变形介绍
局部网格变形,指的是只有部分网格发生变形,其余的网格并不发生变形;也可以是整体网格刚性运动后部分网格块发生变形。基于TFI技术的局部网格变形方法的基本思路是:首先确定网格的变形域及边界,并给定边界的运动形式,该边界包括运动的物面网格和变形域的边界面网格;然后根据需求划分子网格,建立主控点和受控点的对应关系[8],再根据给定的运动形式确定边界点的位移,使用基于弧长的TFI公式计算子网格内部网格点的位移;最后更新网格,得到变形后的网格。
子网格是将网格块每隔若干个网格点取出一个网格点所得到的,子网格划分的示意图如图1所示,将Block1分割成了9个子网格块,A、B、C、D四点为子网格块5的角点。

图1 子网格划分示意图
1.2局部网格变形具体过程
令运动的物面和变形域边界上的网格点为主控点,子网格的角点为受控点,每个受控点可以根据实际情况具有一个或者多个主控点,受控点的位移受到主控点的位移以及与其最近的主控点的距离影响。设xci为子网格块上第i个受控点坐标,xsj为物面上第j个主控点坐标,则两点的距离为
|rij|=‖xci-xsj‖2
(1)
受控点与主控点的距离越近,受控点的变形量受到的影响就越大。通过建立衰减函数确定两者之间的关系,该衰减函数为
(2)
(3)

(4)
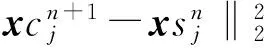
(5)
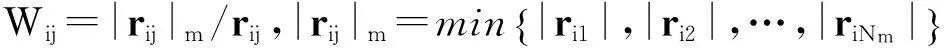
在确定子网格角点位移之后,先对内部网格进行坐标归一化以便使用基于弧长的TFI方法计算内部网格点的位移,弧长归一化的公式为
(6)
(7)
二维TFI的公式为
Δxi,j=U+V-UV
(8)
U=(1-αi,j)Δx1,j+αi,jΔximax,j
(9)
V=(1-βi,j)Δxi,1+βi,jΔxi,jmax
(10)
UV=αi,j(1-βi,j)Δximax,1+βi,j(1-αi,j)Δx1,jmax+
αi,jβi,jΔximax,jmax+(1-αi,j)(1-βi,j)Δx1,1
(11)
1.3流体力学控制方程
CFD在流体域求解守恒型积分的形式适用于动网格的N-S方程[9]
(12)
式中:t为时间;q为守恒变量矢量,表示单位体积的密度、动量和总能量;Ω(t)和∂Ω(t)为控制体积及其边界;n为控制边界∂Ω(t)的外法向;Fc和Fv分别为运输和粘性通量;H为源项。
流动控制方程空间离散采用有限体积方法,无粘通量项采用二阶精度的Roe通量差分分裂迎风格式离散,粘性项采用二阶中心格式进行离散。采用全湍流假设,Sparlart-Allmas湍流模型进行湍流计算。全隐式的方程求解,非定常时间推进采用双时间步法。
2算例验证
2.1NACA0012翼型俯仰振荡
本文使用的动网格方案包括刚性动网格技术和局部网格变形技术,为了验证两种方案的可行性,分别使用上述两种网格技术模拟NACA0012翼型在跨音速流场中绕1/4弦点做俯仰振荡的非定常流场[10],来流马赫数Ma=0.755。翼型迎角的变化规律为
(13)

本算例使用整体网格,网格为C型网格(如图2所示),网格量为16 016,物面附近的网格如图3所示。翼型偏转2.51°后的网格状态如图4所示。

图2 整体网格

图3 物面网格

图4 变形后的网格
从图3~图4可以看出:此时的物面网格仍保持很好的正交性。在小角度的变形幅度下,基于TFI的网格变形技术能够很好地满足变形的需求,并保证了网格质量。由于TFI是一种代数的方法,数值求解时计算网格变形的速度非常快。
计算结果与实验值的对比如图5所示。

(a) CL

(b) CM
从图5可以看出:使用两种方法得到的升力系数和俯仰力矩系数均与实验值吻合良好,表明本文使用的这两种动网格方法均是可行的。
2.2翼型与襟翼共同振荡的数值模拟
2.2.1模型与计算网格
模型的基本翼型是NACA0012,弦长(包含襟翼)c=180mm,其中襟翼的长度是40.69mm,为26.15 c,翼型的旋转轴位于0.35 c处,襟翼的旋转轴位于0.8 c处,实验模型的展长为600mm。计算状态为Ma=0.4,Re=1.63×106,实验模型中,襟翼和翼型之间缝隙的最大距离是0.5mm。该模型的示意图如图6所示[11]。

图6 带有后缘襟翼的翼型
本文使用的网格整体拓扑结构是C形(如图7所示),为了保证襟翼在振荡过程中网格变形后的质量,在翼型周围生成一个O型网格,网格数量为32 192,物面网格点数为263个。
实验中,翼型和襟翼同时在做不同频率的俯仰振荡,因此,本文使用整体网格刚性旋转实现翼型的振荡,而襟翼与翼型之间的偏转使用网格变形来实现。数值模拟的过程中,襟翼的偏转使其附近的流场空间网格发生了变形,然而,在距离襟翼比较远的流场区域内,襟翼偏转引起的网格变形量十分微小,可以忽略。因此,本文采用局部变形的策略(如图8所示),只需图中显示网格的区域发生变形,足以满足襟翼在偏转过程中的网格变形需求。在数值模拟开始前,在参数文件中给定相应的网格变形边界及运动形式,以实现数值模拟过程中的网格局部变形。

图8 局部网格变形策略
2.2.2数值模拟结果及分析
通过求解N-S方程,对带襟翼偏转运动的翼型俯仰振荡进行非定常求解。其中,翼型的俯仰振荡控制方程为
α(t)=α0+Δαsin(ωαt+φα)
(14)
式中:α(t)为翼型整体的实时迎角;α0为翼型整体振动的初始迎角;Δα为翼型整体振荡的幅值迎角;ωα为振动圆频率;φα为相位差。
襟翼偏转的运动控制方程为
δ(t)=δ0+Δδsin(ωδt+φδ)
(15)
式中:δ(t)为襟翼的实时偏转角;δ0为襟翼的初始偏转角;Δδ为襟翼的偏转角幅值;ωδ为振荡频率;φδ为相位差。
该系统的真实运动形式为方程(14)和方程(15)的叠加。
对带襟翼翼型的两种运动状态进行计算,并与实验值进行对比,其中两种状态的计算使用同一套网格。
(1) 状态一
该状态下,带襟翼偏转运动的翼型俯仰振荡的运动方程为

(16)
该运动方程如图9所示。通过非定常求解,升力系数迟滞环曲线和俯仰力矩系数迟滞环曲线如图10所示,并与文献[11]中的实验值进行对比。从图10可以看出:计算结果与实验值吻合良好;初始迎角为0°,幅值迎角为6°,迎角范围为(-6°,6°),在此基础上,襟翼偏角为(-5°,6°),因此本文所使用的方法对于小迎角范围内的襟翼动态偏转问题可以进行较好地数值模拟,具有一定的计算精度;由于迎角振荡频率为襟翼偏转频率的一半,因此迟滞环曲线具有明显的交叉。
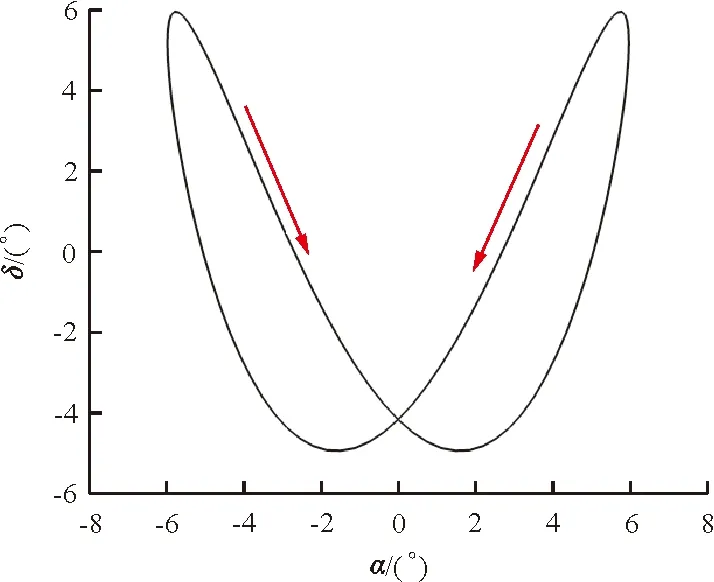
图9 翼型迎角和襟翼偏角运动规律(状态一)
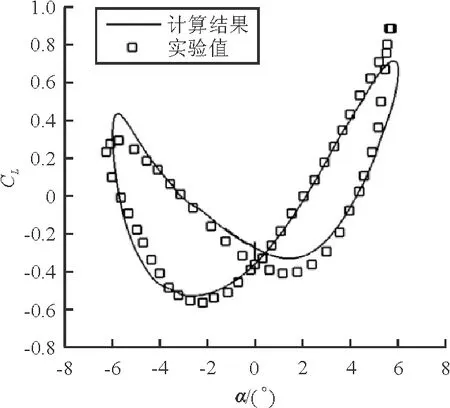
(a) CL

(b) CM
一个周期内带襟翼翼型的动态变化流场压力系数云图及襟翼处的局面网格细节图如图11所示。襟翼偏转后,仍然保有较好的局部网格质量,因此本文所使用的网格变形方法对襟翼偏转问题具有较好的适用性。
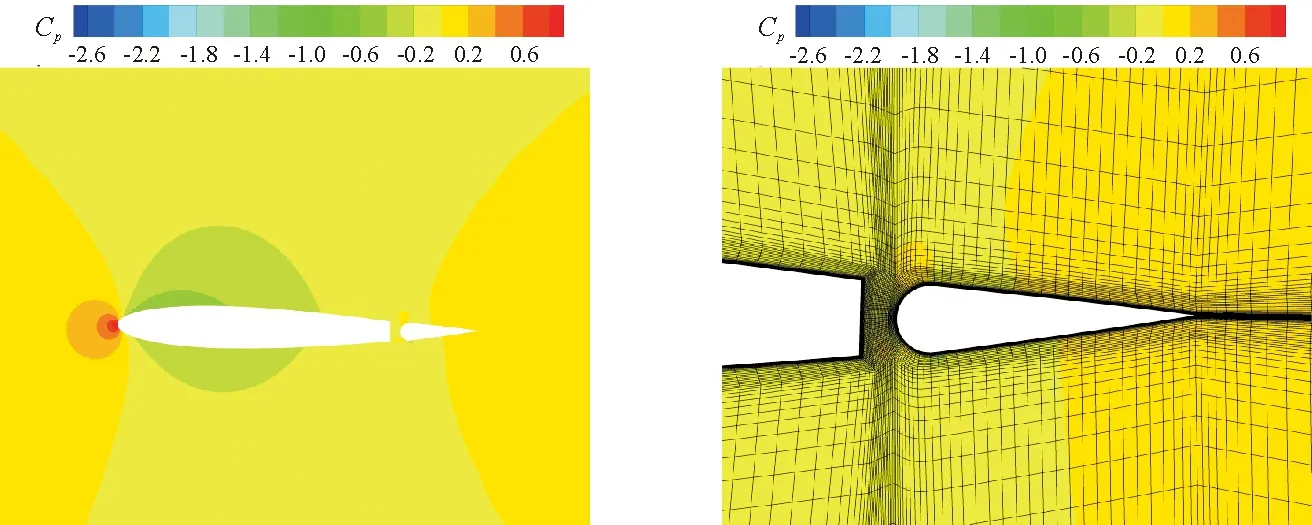
(a1) 压力系数云图 (a2) 局部网格细节
(a)t=0.005T

(b1) 压力系数云图 (b2) 局部网格细节
(b)t=0.125T

(c1) 压力系数云图 (c2) 局部网格细节
(c)t=0.250T

(d1) 压力系数云图 (d2) 局部网格细节
(d)t=0.375T
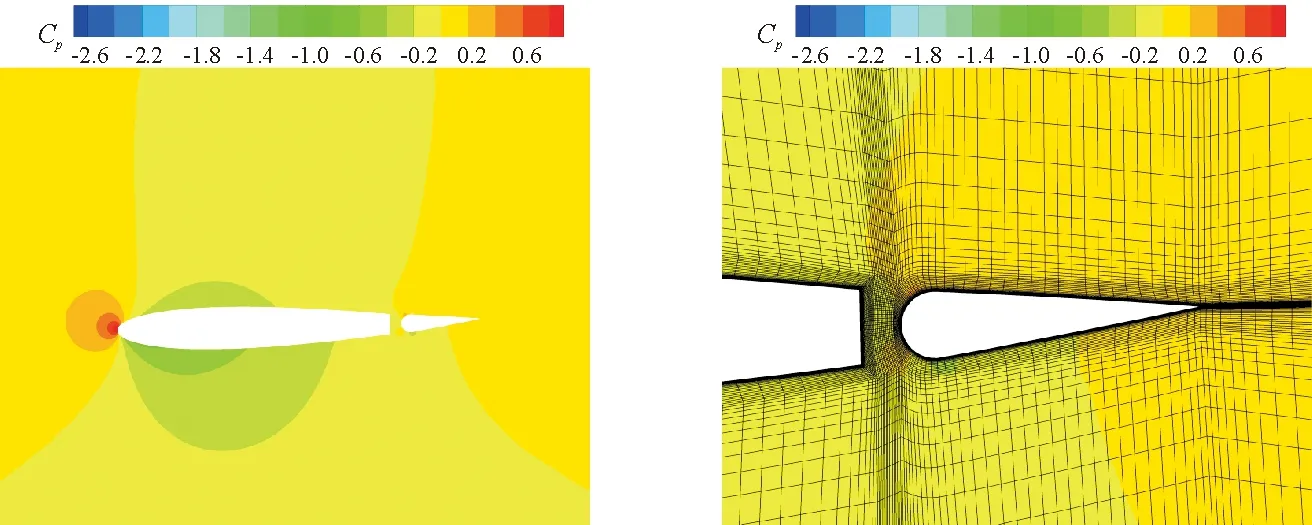
(e1) 压力系数云图 (e2) 局部网格细节
(e)t=0.500T

(f1) 压力系数云图 (f2) 局部网格细节
(f)t=0.625T

(g1) 压力系数云图 (g2) 局部网格细节
(g)t=0.750T

(h1) 压力系数云图 (h2) 局部网格细节
(h)t=0.875T
图11各时间节点的压力系数云图及局部网格细节
Fig.11Cpcontours and local mesh details of each time node
从图11可以看出:在t=0.005T时,翼型为正迎角,具有抬头角速度,襟翼偏转角为负值(根据飞行力学定义,襟翼下偏为正),且具有向下偏转的角速度,此时翼型上表面低压区较强,但由于襟翼上偏,因此翼型整体具有负升力;在t=0.125T时,翼型为正迎角,具有抬头角速度,襟翼偏转角为正值,此时翼型上表面低压区较强,翼型整体具有正升力;在t=0.250T时,翼型为正迎角,且达到峰值,襟翼偏转角为正值,且具有向上偏转的角速度,翼型整体具有正升力;在t=0.375T时,翼型为正迎角,具有低头角速度,襟翼偏转角为负值;在t=0.500T时,翼型为负迎角,具有低头角速度,襟翼偏转角为负值,翼型整体升力为负值;在t=0.625T时,翼型为负迎角,翼型上表面高压区较强,尽管襟翼偏转角为正值,但翼型整体升力为负值;在t=0.750T时,翼型为负迎角,达到迎角峰值,襟翼偏转角为正值,达到襟翼偏角峰值,翼型整体升力为正值;在t=0.875T时,翼型为负迎角,襟翼偏转角为负值,翼型整体升力为负值。
(2) 状态二
该状态下,带襟翼偏转运动的翼型俯仰振动的运动方程为

(17)
该运动方程如图12所示。

图12 翼型迎角和襟翼偏角运动规律图(状态二)
通过非定常求解,升力系数迟滞环曲线和俯仰力矩系数迟滞环曲线如图13所示,并与文献[11]中的实验值进行对比。
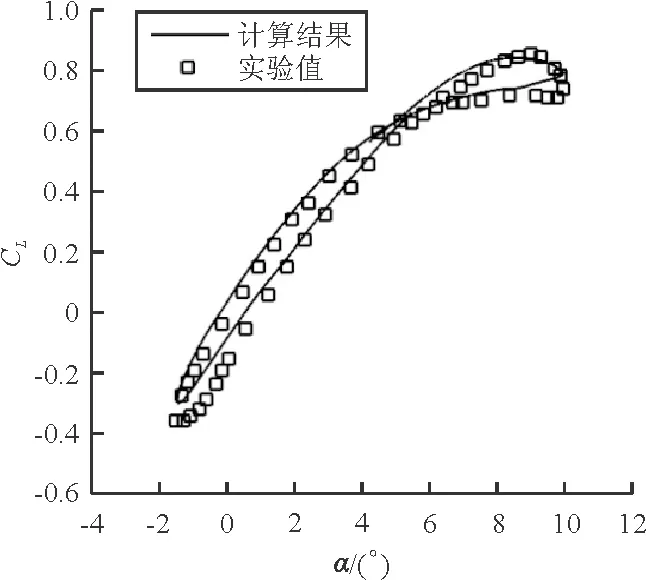
(a) CL

(b) CM
从图13可以看出:计算结果与实验值吻合良好;初始迎角为4.25°,幅值迎角为5.75°,迎角范围为(-1.5°,10°),在此基础上,襟翼偏角为(-6°,5°),因此本文所使用的方法对于中等迎角范围内的襟翼动态偏转问题可以进行较好地数值模拟,具有一定的计算精度。
3结论
(1) 本文发展了一套基于TFI技术的局部网格变形方法,该方法能够在保证计算精度的情况下提高计算效率,并且可以较好地配合其他动网格技术以模拟有多部件相对运动的复杂流场。
(2) 本文结合局部网格变形方法和刚性动网格方法数值模拟了NACA0012翼型与襟翼以不同频率进行俯仰振荡的复杂流场,变形后的网格依然具有很好的网格质量,将计算结果与实验值进行对比,验证了本文发展方法的可行性。
(3) 本文仅介绍了局部网格变形方法在二维问题上的应用,对于带副翼动态偏转的三维问题,也可以使用该方法结合动态面搭接技术进行数值模拟,从而有效地解决由于副翼偏转引起的“剪刀差”问题。
参考文献
[1] 杨国伟, 钱卫. 飞行器跨声速气动弹性数值分析[J]. 力学学报, 2005, 37(6): 769-776.
Yang Guowei, Qian Wei. Numerical analyses of transonic flutter on an aircraft[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(6): 769-776. (in Chinese)
[2] Eriksson L E. Generation of boundary-conforming grids around wing-body configurations using transfinite interpolation[J]. AIAA Journal, 1982(20): 1313-1320.
[3] Dubuc L, Cantariti F, Woodgate M, et al. A grid deformation technique for unsteady flow computations[J]. International Journal for Numerical Methods in Fluids, 2000, 32(3): 285-311.
[4] 袁先旭. 非定常流动数值模拟及飞行器动态特性分析研究[D]. 绵阳:中国空气动力研究与发展中心, 2004.
Yuan Xianxu. Numerical simulation of unsteady flow and dynamic characteristics research of aircraft[D]. Mianyang: Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, 2004.(in Chinese)
[5] 张兵, 韩景龙. 带旋转修正的弹簧TFI-混合动网格方法[J]. 航空学报, 2011, 32(10): 1815-1823.
Zhang Bing, Han Jinglong. Spring-TFI hybrid dynamic mesh method with rotation correction[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1815-1823.(in Chinese)
[6] 李喜乐, 杨永. 带副翼偏转的三角翼自由滚转运动数值模拟[J]. 航空学报, 2012, 33(3): 453-462.
Li Xile, Yang Yong. Numerical simulation of the free rolling motion of a delta wing configuration with aileron deflection[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 453-462.(in Chinese)
[7] 夏贞锋, 杨永. 螺旋桨滑流与机翼气动干扰的非定常数值模拟[J]. 航空学报, 2011, 32(7): 1195-1201.
Xia Zhenfeng, Yang Yong. Unsteady numerical simulation of interaction effects of propeller and wing[J]. Acta Aeronauticaet Astronautica Sinica, 2011, 32(7): 1195-1201.(in Chinese)
[8] Peter M Hartwich, Shreekant Agrawal. Method for perturbing multiblock patched grids in aeroelastic and design optimization applications[R]. AIAA-97-2038, 1997.
[9] Anderson John D, Jr. Fundamentals of aerodynamics[M]. New York: McGraw-Hill Book Company, 2007.
[10] Landon R H. NACA0012 oscillation and transient pitching[R]. Compendium of Unsteady Aerodynamic Measurements, Data Set 3, AGARD-R-702, 1982.
[11] Andrzej Krzysiak, Janusz Narkiewicz. Aerodynamic loads on airfoil with trailing-edge flap pitching with different frequencies[J]. Journal of Aircraft, 2006, 43(2): 407-418.
Investigation on Local Grid Deformation Method Based on TFI
Yang Weilong, Yang Yong
(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)
Abstract:Global mesh deformation technique has influence on other dynamic grid methods, so it is difficult to be combined with other dynamic grid methods to solve complex flow problems. A local grid deformation method based on TFI(Transfinite Interpolation) is developed. This method, which is different from other global grid deformation methods, is that it can limit the deformation in specific zones without any influence on grids of other zones, so it will not hamper the use of other dynamic grid methods. For an airfoil NACA0012 with a flap, numerical simulations of pitching oscillations are conducted, and computational results agrees well with experimental results. Then it is concluded that the method developed in this paper is viable for flow solutions of complex geometries.
Key words:flap deflection; grid deformation; pitching oscillation; unsteady flow; transfinite interpolation
收稿日期:2016-04-01;修回日期:2016-04-25
通信作者:杨维龙,ywlvs@163.com
文章编号:1674-8190(2016)02-216-09
中图分类号:V211.3
文献标识码:A
DOI:10.16615/j.cnki.1674-8190.2016.02.012
作者简介:
杨维龙(1988-),男,硕士研究生。主要研究方向:动网格技术。
杨永(1962-),男,博士,教授,博导。主要研究方向:空气动力学、计算流体力学和设计空气动力学。
(编辑:赵毓梅)
