田径场地弯道弧线起跑线的直弦丈量法

辽宁省朝阳工程技术学校 张振河

一、前言

在田径项目中，有些是不分道进行的比赛。如标准跑道举行3000m以上的比赛都不分道，在弯道起跑(不分道)时，必须力求使每一个运动员所跑的初段距离相等。为了达到规则的要求，不分道跑的项目的起跑线，必须是一条弧线，而弯道上的弧线起跑线画法就目前国内外一些画法比较麻烦，在实际中不易操作，本文研究就是利用数学原理，找出一种比较简捷的放射线丈量法，弧线连接丈量点，这样就会很快的画出弯道弧线起跑线，即简单又快捷。解决了广大体育工作者画场地难的问题。

二、研究方法

半圆式田径场地弯道弧线起跑线，在数学当中也就是一个圆的渐开线轨迹。根据数学圆的渐开线极坐标参数方程，找出这条渐开线轨迹与八条分道线外沿交点，这也就是本文所要研究的弧线起跑线的放射式丈量点。根据极坐标参数方程分别求出每条分道放射线所对的圆心角，再根据数学余弦定理，求出圆心角所对应的边长(放射线的长度)，然后把每条放射线丈量点用弧线连 接，这条弧线就是弯道弧线起跑线。如图所示：M(ρ.θ) 是圆的渐开线上的任意一点, B为圆的切点，圆的极坐参数方程：

即：

以标准400米半圆式田径场地，场地半径 R36m、分道宽1.22m为例。每条分道放射线长S18所对的圆心角度分别是θ1……θ8。 计算线半径R=（36+0.3）m，ρ1……ρ8代表八条分道线的外沿半径。t18分别是八条分道丈量点与圆的切线所对的圆心角。则由

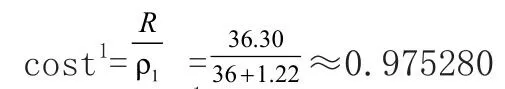
查表得：t1=12 .765623°

同理：t2=19.208282° t3=23.754495°W

4=27.381395°W

5=30.431789°W

6=33.075712°W

7=35.412860°W

8= 37.507916°

根据上述公式：

同理：

从图可以看出：△AOD为任意三角形，OD是跑道计算线半径R，ρ是第一分道线半径,∠AOB上述已计算出来，在任意三角形中已知两边和它们的夹角，第三边之长可以用余弦定理计算。即

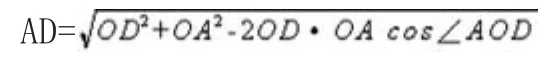
上面公式可写成(现以第一道放射线为例)

同理：

上式S18放射线已求出，然后在场地的一或三直段分界线上，从内突沿外沿向外丈量0.3米得一点，以此点为圆心，分别以S18为半径画弧，分别与分道线外沿相交，交点也就是放射线丈量点，然后用弧线连接交点，此弧线即为起跑线的后沿；也就是弯道弧线起跑线。如图（1-2）

弧线起跑线集合线的画法：如图(1-3)把弧线起跑线向后平行移动3m即为弧线起跑线的集合线,方法是把D点向后丈量3m交于第一道跑道计算线 D′处,以D′为丈量起点,分别经(S1′……S8′)到S ……S点0.93m+3m 2.2m+3m 3.15m+3m 4.83m+3m 6.20m+3m 7.61m+3m 9.04m+3m 10.52m+3m. 把(S1′ ……S8′)的点用弧线的虚线连接.这条虚线的弧线就是弯道起跑线的集合线。

三、结论

此方法可适用于所有半圆式田径场地弯道起跑线画法，其计算公式可作为经验公式。

此方法比较其它方法，便于实际操作，快速、简单易行。