高斯混合分布下雷达目标距离检测方法

2016-06-22赵兴刚王首勇

电波科学学报 2016年2期

赵兴刚　王首勇

(空军预警学院,武汉 430019)

高斯混合分布下雷达目标距离检测方法

赵兴刚王首勇

(空军预警学院,武汉 430019)

摘要在非高斯相关杂波背景下,传统检测方法难以检测到目标,基于球不变随机过程杂波的似然比检测方法通过对杂波准确建模,可以取得较好的检测效果,但由于其分布形式往往较为复杂,一般情况下很难得到检测统计量的闭合形式．针对该问题,基于信息几何理论,通过计算高斯混合统计流形上两分布间的距离,定义了一种距离检测器,该检测器通过计算估计分布与目标有无两种假设分布间的距离差,来实现目标检测,将检测问题转化为统计流形上的几何问题．仿真和实测数据验证结果表明:在复杂杂波背景下,与传统方法相比,该方法具有更好的检测性能,且易于实现．

关键词信息几何;统计流形;测地线距离;Kullback-Leibler分离度

引言

现代雷达探测目标有时会面临很强的地、海杂波,这类杂波通常呈现出显著的非高斯相关特性,杂波尖峰显著,概率密度函数拖尾严重,频域上也存在目标多普勒频率与强杂波谱区交叠的情况．由于以上问题的存在,使得传统的检测技术几乎难以检测到这类目标,对此国内外专家提出了很多新的检测方法[1-3],比较有代表性的是基于球不变随机过程(Spherically Invariant Random Process, SIRP)杂波的似然比统计检测方法.该方法通过利用SIRP分布模型对杂波进行建模,能比较准确地描述杂波的非高斯和相关特性,在此基础上推导出的似然比检测统计量,能在复杂杂波背景下取得较好的检测性能,但由于SIRP杂波分布形式往往较为复杂,除了少数分布形式,一般情况下很难得到检测统计量的闭合形式,某些特定分布下推导出的检测统计量形式也非常复杂,难以实现．信息几何(Information Geometry)是近年来发展起来的用微分几何的方法研究统计学问题的一门新兴学科,已在多个领域得到广泛应用,如法国人Barbaresco将信息几何应用在了多普勒雷达恒虚警检测、空时自适应处理等方面[4-6],改善了多普勒雷达成像和检测的性能．

利用信息几何解决雷达目标检测问题,首先要建立杂波分布统计流形,在非高斯相关杂波背景下,描述杂波的分布形式有多种,其中高斯混合分布通过改变模型参数几乎可以拟合任何的分布类型[7],具有广泛的通用性．因而文中利用高斯混合分布建立杂波统计流形,通过计算得到两高斯混合分布之间的距离,定义了一种距离检测器．该检测器通过计算由观测数据估计得到的分布与目标有无两种假设分布之间的距离差,来实现目标的检测,将检测问题转化为了统计流形上的几何问题．仿真和实测数据验证结果表明,在复杂杂波背景下,该方法具有更好的检测性能,且形式简单,易于实现．

1信息几何中的距离

设随机矢量x服从的联合概率密度函数为f(x),通过参数θ定义概率分布族

S={f(x|θ)|θ∈Rn}．

(1)

向量θ=(θ1,θ2,…,θn)T的每一组取值都代表了S中的一个概率密度函数,即S由θ参数化,则在一定的拓扑结构下概率分布族S构成一个以θ为坐标的微分流形,称为统计流形．在黎曼几何中,流形定义为局部同胚于欧式空间的拓扑空间,维数没有限制．统计流形上的黎曼度量由Fisher信息矩阵G(θ)=[gij(θ)]给出,其中

(2)

统计流形上相邻两个分布f(x|θ)和f(x|θ+dθ)之间的微分距离由Fisher信息矩阵给出:

ds2=dθTG(θ)dθ．

(3)

考虑连接统计流形上两点θ1和θ2的任意曲线θ(t),其中t1≤t≤t2为自由变量,且θ(t1)=θ1,θ(t2)=θ2．统计流形上两点f(x|θ1)和f(x|θ2)之间沿曲线θ(t)的距离[8]为

(4)

显然,该距离的大小取决于曲线θ(t)的选取,流形上连接两点的所有曲线的最小长度为Fisher信息距离,即

(5)

式中,DF(θ1,θ2)对应的最短曲线γ(t)对应了流形上两点间的最短测地线,故也称为测地线距离．测地线可以看做欧式空间中的直线在流形中的推广．

2非高斯杂波下的距离检测器

由式(5)可知,计算流形上两点间的测地线距离需求解复杂的积分式,因而,除一些特殊的统计流形外,通常计算测地线距离是非常困难的．实际上,流形上的距离有多种定义方式,在一定距离范围内,测地线距离可以由K-L分离度(Kullback Leibler Divergence, KLD)来代替[9],其定义为

DKL[f(x|θ1)‖f(x|θ2)]

=E{lnf(x|θ1)-lnf(x|θ2)}．

(6)

KLD提供了度量两个概率分布间距离的一种方式,相比于测地线距离而言,KLD更容易计算．描述非高斯相关杂波的分布形式有多种,其中,高斯混合分布(Gaussian Mixture Distribution, GMD)模型通过改变模型参数几乎可以拟合任何其他分布,在多个领域具有广泛应用[7]．下面,通过定义高斯混合分布流形,并计算得到流形上两GMD间的KLD,进而得到非高斯相关杂波背景下基于KLD的距离检测器．

2.1高斯混合分布流形

令随机矢量x服从的分布模型为GMD,其定义为

(7)

式中:Nk(x;μk,Rk)表示GMD的第k个高斯分量,其均值矢量为μk,协方差矩阵为Rk;λk是第k个高斯分量的混合系数．通过改变模型的这些参数,GMD能够近似很多复杂的概率分布情况．根据式(1)定义高斯混合分布流形为

SGMD={f(x|θ)|θ∈R3K}．

(8)

式中,θ=(λ1,λ2,…,λK,μ1,μ2,…,μK,R1,R2,…,RK)为高斯混合分布流形的坐标．

2.2基于GMD的距离检测方法

两GMD之间的KLD为

DKL[f(x|θ1)‖f(x|θ2)]

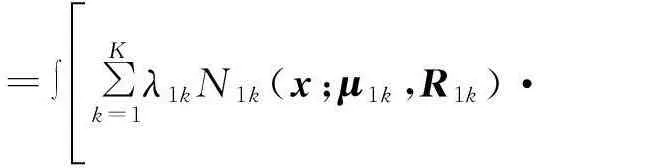
= ∫éëêêê∑Kk=1λ1kN1k(x;μ1k,R1k)·

(9)

对于式(9)而言,一般情况下采用两种方法来计算[10]:一种是基于采样的蒙特卡洛方法;另一种是通过其KLD上界来近似．蒙特卡洛方法需采样生成大量样本数据,计算量较大,而KLD上界可由模型参数直接估计．

引理1(对数求和不等式)对于非负数a1,a2,…,aN和b1,b2,…,bN,有下式成立:

(10)

如果an/bn=C,则等式成立．

根据引理1,式(9)可以写为

DKL[f(x|θ1)‖f(x|θ2)]

= ∑Kk=1λ1klgλ1kλ2k+∑Kk=1λ1kKLD(N1k(x;μ1k

R1k)‖N2k(x;μ2k,R2k))．

(11)

两高斯分布之间的KLD由下式计算得到:

DKL(N1k(x;μ1k,R1k)‖N2k(x;μ2k,R2k))

= 12ln|R1k||R2k|æèçöø÷+tr(R-11kR2k)+éëêê

(12)

式中: |·|和tr分别表示矩阵的行列式和迹;N为高斯分布的维数．

至此,考虑在实际雷达系统中杂波服从GMD的情况,设雷达中某个距离单元观测的复包络信号为

x(n)=s(n)+v(n),

n=0,1,…,N-1．

(13)

式中:s(n)=αejωn,α为信号复幅度,ω=fd/fr,fd为目标的多普勒频率,fr为脉冲重复频率;N为CPI长度;v(n)为杂波序列,服从GMD．设观测信号矢量x=[x(0),x(1),…,x(N-1)]T,那么式(13)的矢量形式为

x=s+v．

(14)

式中: s=α[1,ejω,…,ejω(N-1)]T; v=[v(1),v(2),…,v[N-1]]T．在实际应用中,需要先根据观测数据来估计GMD模型参数,常用的算法为期望最大化(Expectation Maximization, EM)算法[11],要使用EM算法,需定义完整的和不完整的数据集,观测矢量x=[x(0),x(1),…,x(N-1)]T是不完整的数据,完整的数据可以被看作是带有标志的观测矢量,以此表明产生该混合高斯模型的分量,完整的数据可以定义为

y(m)=[x(m),k],

m=0,1,…,M-1,k∈(1,…,K)．

(15)

式中,观测数据x(m)的标记k,表示混合密度的第k个分量．EM算法的主要步骤是在给定观测数据和参数矢量当前估计的条件下,定义完整数据的期望为

U(θ,^θ(i)) =E[lnf(y(m);θ)|x(m);^θ(i)]

(16)

式中: θ={θk=[λk,μk,Rk],k=1,…,K}为GMD模型的参数;i为EM算法的迭代次数; x(m)与混合密度第k个高斯分量的联合分布函数为

f(x(m),k|^θ(i)) =^λ(i)kf[x(m)|^θ(i)k]

(17)

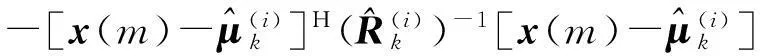
(18)

作为K个高斯密度混合的x(m),其分布函数为

f(x(m)|^θ(i)) =N[x(m)|^θ(i)]

(19)

将式(17)和式(19)代入式(16)可得

U(θ,^θi)= ∑N-1m=0∑Kk=1{^λ(i)kNk[x(m);^μ(i)k,^R(i)k]N[x(m)|^θ(i)]·

(20)

采用约束优化方法,相对于λk对式(20)进行最大化,即对式(20)相对于λk求导数,并令其为零,得

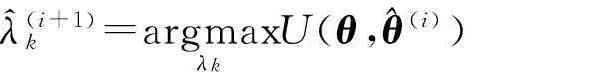
^λ(i+1)k =argmaxλkU(θ,^θ(i))

(21)

^μ(i+1)k =argmaxμkU(θ,^θ(i))

(22)

(23)

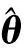
(24)

TGMD=DKL(f(x|θx),f(x|θH0))-

DKL(f(x|θx),f(x|θH1))>η．

(25)

图1　距离检测器实现框图

3仿真分析与实测数据验证

3.1检测性能仿真分析

利用MATLAB仿真产生GMD杂波数据,来验证GMD-DD的检测性能,并与基于SIRP的广义似然比检测(SIRP-Generalized LikelihoodRatio Test, SIRP-GLRT)[12]方法以及传统的MTD技术进行比较分析．

首先对仿真产生的GMD杂波进行分析,图2给出了杂波数据的时域分布和功率谱密度曲线．

从图2可以看出,GMD杂波有较强的非高斯相关特性,脉冲尖峰特征明显,杂波功率谱展宽．

在使用GMD-DD进行检测之前,需要首先估计杂波模型参数,即θ=(λ1,λ2,μ1,μ2,R1,R2),式(21)～(23)给出了GMD模型参数估计的EM算法,这里采用矩估计方法得到迭代的初始值,表1给出了混合系数λ1,λ2的三组估计结果．

(a) 时域分布

(b) 功率谱图2　GMD杂波数据时域分布和功率谱密度曲线

参数值第1组λ1λ2第2组λ1λ2第3组λ1λ2真实值0.30.70.40.60.50.5EM估计值0.320.670.380.610.510.48

从表1可以看出,EM算法对GMD模型参数具有较高的估计精度．估计得到GMD模型参数后就可以利用GMD-DD对目标进行检测,GMD-DD是通过比较估计分布与两种假设分布之间距离差来实现目标检测的,图3给出了随着信杂比(Signal to Clutter Ratio, SCR)的变化这两个距离的变化曲线．

令目标多普勒频率fd=62.5Hz,由图2(b)可知目标处于强杂波谱区,给出此时GMD-DD、SIRP-GLRT、MTD的检测性能比较曲线,如图4所示．

图3　估计分布与两假设分布之间的KLD变化曲线

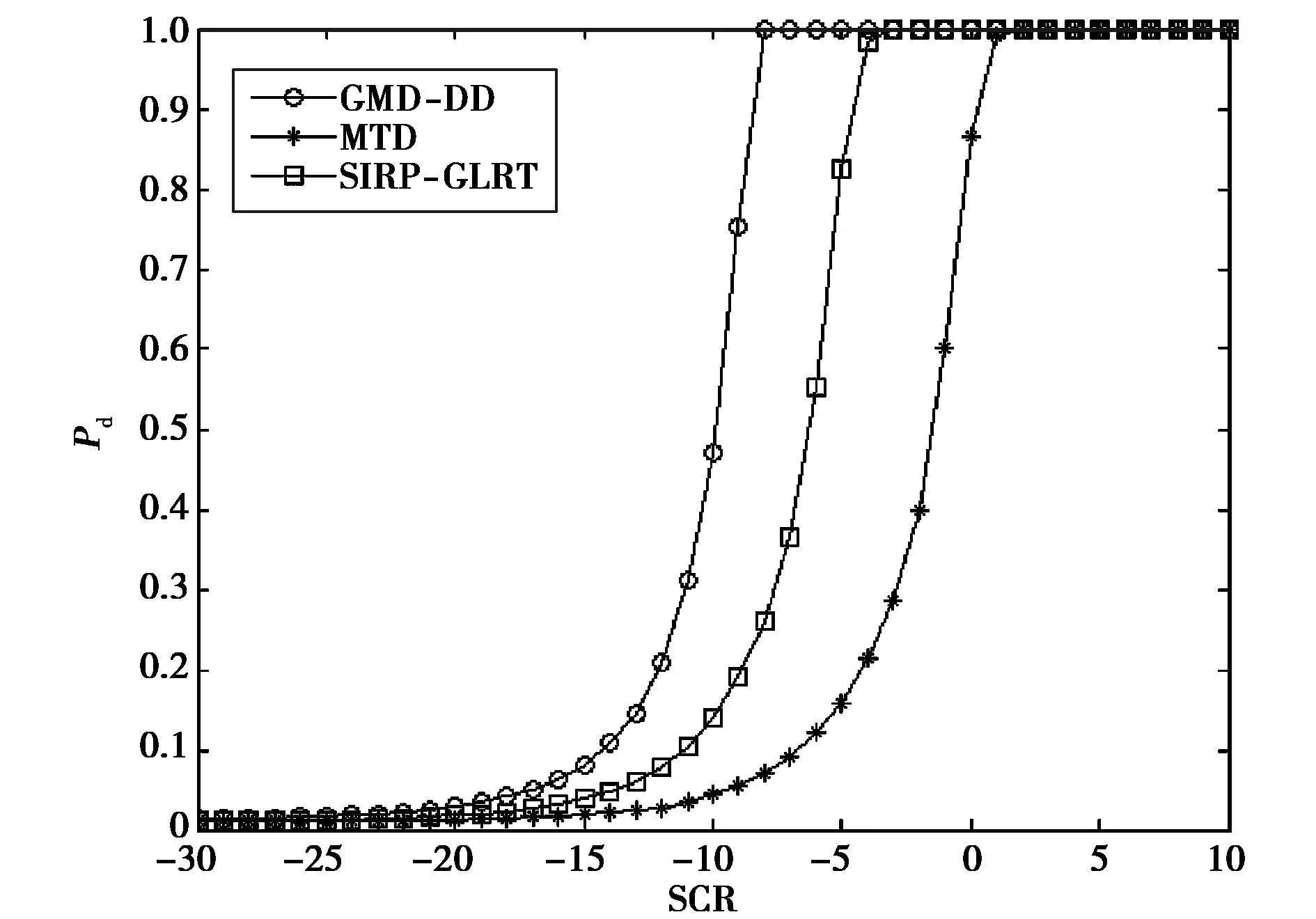
图4　fd=62.5 Hz时三种方法检测性能比较曲线

在此,SIRP-GLRT检测方法利用K分布来描述杂波．从图4可以看出,当目标处于强杂波谱区时,GMD-DD的检测性能当检测概率为0.5时比SIRP-GLRT和MTD分别改善了约2dB和8dB．比较图3和图4可以看出,估计分布与假设分布间距离的变化与GMD-DD检测性能的变化趋势是一致的．

为进一步观察三种算法在目标处于不同情况下的检测性能,图5给出了多普勒频率fd=250Hz时的检测性能比较曲线,此时,由图2(b)可知,目标处于非强杂波谱区．

从图5可以看出,当目标处于非强杂波谱区时,三种算法的检测性能都有所改善．与图4相比,三种算法间性能的差别变小,检测概率为0.5时,GMD-DD与SIRP-GLRT和MTD相比,检测性能分别提高了约2dB和5dB．其中MTD与图4相比,检测性能改善幅度较大,这也说明了杂波的功率谱宽度对MTD的检测性能影响较大．

图5　fd=250 Hz时三种方法检测性能比较曲线

3.2实测数据下的性能分析

这里采用的是加拿大McMaster大学提供的IPIX海杂波[13]#320组数据,通过添加仿真目标信号,比较分析了不同SCR、不同目标多普勒频率条件下GMD-DD与SIRP-GLRT、MTD的检测性能．

图6给出了实测海杂波数据的功率谱密度曲线,可以看出杂波谱明显展宽,主杂波谱3dB带宽为[-160Hz,-50Hz]．根据谱密度曲线,选取目标多普勒频率分别为fd=-100Hz和fd=375Hz,其余信号取值同§3.1．

图6　#320组数据样本的功率谱密度曲线

首先给出目标多普勒频率fd=-100Hz时,三种方法的检测曲线,如图7所示．可以看出与仿真数据不同的是,GMD-DD与SIRP-GLRT相比,性能改善程度明显减小,改善了约0.5dB.这是因为仿真数据直接产生的是GMD杂波数据,SIRP-GLRT是利用K分布来拟合杂波,与之相比,GMD-DD在检测时杂波拟合和参数估计精度会更高,所以检测性能改善幅度较大.在采用实测数据后,高斯混合分布的拟合精度下降,且为了提高实时性,这里EM算法采用了较少的迭代次数,则GMD-DD参数估计的优势减弱,检测性能也会相应受到影响．

图8给出了目标信号在弱杂波谱区即fd=375Hz时三种方法的检测性能比较曲线.可以看出与图7相比,三种方法检测性能都有所提高,GMD-DD较SIRP-GLRT和MTD相比,检测性能分别改善了0.8dB和9dB．

图7　fd=-100 Hz时三种方法检测性能比较曲线

图8　fd=375 Hz时三种方法在实测数据下检测性能比较曲线

4结论

论文首先利用EM算法估计GMD模型参数,然后计算得到两GMD间的KLD,得到了高斯混合分布下基于KLD的距离检测器,最后,通过与SIRP-GLRT和MTD进行检测性能比较,说明了该距离检测器在复杂背景下具有较好的检测性能．为了分析计算方便,论文在仿真实验中只用了两个高斯分布混合的情况,而在实际应用中,可以根据实际杂波背景和硬件条件来选择合适的混合分布数量,以保证较好的检测性能．

参考文献

[1]扈罗全, 林乐科, 朱洪波. 三种重拖尾分布海杂波的比较与分析[J]. 电波科学学报, 2007, 22(6): 1061-1067.

HULQ,LINLK,ZHUHB.Comparisonandanalysisofthreekindsofdistributionofseaclutterwithheavytails[J].Chinesejournalofradioscience, 2007, 22(6):1061-1067.(inChinese)

[2] 冯迅, 王首勇, 万洋, 等. 非高斯相关杂波背景下雷达目标统计检测方法[J].电波科学学报, 2012, 27(5): 1005-1011.

FENGX,WANGSY,WANY,etal.Radartargetstatisticaltestincorrelatednon-Gaussianclutterbackgrounds[J].Chinesejournalofradioscience, 2012, 27(5):1005-1011. (inChinese)

[3] 朱晓波, 王首勇, 冯迅. 基于分数低阶本征滤波的雷达目标检测方法[J].电波科学学报, 2012, 27(1): 165-171.

ZHUXB,WANGSY,FENGX.Radartargetdetectionmethodbasedonfractionallowerordereigenfilter[J].Chinesejournalofradioscience, 2012, 27(1):165-171. (inChinese)

[4]BARBARESCOF.NewfoundationofradarDopplersignalprocessingbasedonadvanceddifferentialgeometryofsymmetricspaces:DopplermatrixCFARandradarapplication[C]//InternationalRadarConference.Bordeaux, 2009.

[5]BARBARESCOF.RobuststatisticalradarprocessinginFréchetmetricspace:OS-HDR-CFARandOS-STAPprocessinginsiegelhomogeneousboundeddomains[C]//InternationalRadarSymposium(IRS'11).Leipzig, 2011.

[6]WANGXZ,CHENGYQ,MORELANDEM,BillMoran.Bearings-onlysensortrajectoryschedulingusingaccumulativeinformation[C]//ProceedingsofInternationalRadarSymposium.Leipzig,Germany, 2011, 682-688.

[7]ZHAOYX,ZHUANGXH.Gaussianmixturedensitymodelingofnon-Gaussiansourceforautoregressiveprocess[J].IEEEtransactionsonsignalprocessing, 1995, 43(4): 894-903.

[8]MENENDEZML,MORALESD,PARDOL,etal.Statisticaltestsbasedongeodesicdistance[J].Appliedmathematicsletters,1995, 8(1): 65-69.

[9]AMARIS.Informationgeometryonhierarchyofprobabilitydistributions[J].IEEEtransactionsoninformationtheory, 2001, 47(5): 1701-1711.

[10]VASCONCELOSN.Ontheefficientevaluationofprobabilisticsimilarityfunctionsforimageretrieval[J].IEEEtransactionsoninformationtheory, 2004, 50(7): 1482-1496.

[11]MOONTK.Theexpectationmaximizationalgorithm[J].IEEEsignalprocessingmagazine,1996,13(6):47-60.

[12]王首勇, 万洋, 刘俊凯, 等.现代雷达目标检测理论与方法[M].北京: 科学出版社, 2014.

[13]REMBRANDTB,BRIANC.TheMcMasterIPIXradarseaclutterdatabase[EB/OL].(2014-03-12)[2015-05-17].http://soma.ece.mcmaster.ca/ipix/dartmouth/datasets.htm.

Distance detection method to radar target under Gaussian mixture distribution

ZHAO XinggangWANG Shouyong

(AirForceEarlyWarningAcademy,Wuhan430019,China)

AbstractIt is hard for traditional methods to detect targets in correlated non-Gaussian clutter backgrounds. The likelihood ratio test based on spherically invariant random process clutter could get good performance by modeling clutter accurately. However, it is very hard to get closed form of test statistical magnitude for that the probability distribution function form is usually complicated. Based on information geometry theory, the distance detector is defined by comparing the distance between the distribution estimated by observation data and two hypothetical distributions, translating detecting problem into geometry problem on statistical manifold. Simulation results show that detection performance of distance detector under correlated non-Gaussian clutter backgrounds outperforms traditional methods,simultaneously,it can be easily operated.

Keywordsinformation geometry; statistical manifold;geodesic distance; Kullback-Leibler divergence

收稿日期：2015-05-17

中图分类号TN957.51

文献标志码A

文章编号1005-0388(2016)02-0346-07

DOI10.13443/j.cjors.2015051701

作者简介

赵兴刚(1988-),男,山东人,空军预警学院信息与通信处理专业博士研究生,研究方向为雷达目标检测．

王首勇(1956-),男,河南人,空军预警学院教授,博士生导师,主要研究方向为雷达信号处理．

赵兴刚, 王首勇. 高斯混合分布下雷达目标距离检测方法[J]. 电波科学学报,2016,31(2):346-352. DOI: 10.13443/j.cjors.2015051701

ZHAO X G, WANG S Y. Distance detection method to radar target under Gaussian mixture distribution[J]. Chinese journal of radio science,2016,31(2):346-352. (in Chinese). DOI: 10.13443/j.cjors.2015051701

资助项目: 国家自然科学基金(61179014)；青年科学基金(61302193)

联系人：赵兴刚 E-mail: 565484636@qq.com

电波科学学报

2016年2期

高斯混合分布下雷达目标距离检测方法

杂志排行

电波科学学报的其它文章