国际原油与黄金价格的风险传染关系研究
2016-06-22张清朵熊学文
张清朵, 杨 坤, 熊学文
国际原油与黄金价格的风险传染关系研究
张清朵1, 杨坤1, 熊学文2
(1.成都理工大学 商学院, 四川 成都 610059; 2.重庆文理学院 经济管理学院, 重庆 永川 402160)
关键词:国际原油;国际黄金;大宗商品市场;风险依存度;风险传染;溢出效应;金融风险
摘要:以WTI原油期货价格和伦敦黄金定盘价作为研究对象,通过构建Copula模型明确市场间的风险相依强度,并结合使用向量自回归(VAR)模型对其风险传染方向进行研究。研究结果表明:国际原油价格和国际黄金价格之间存在着明显的动态风险相依关系与双向风险溢出效应。相对而言,国际原油价格波动传染到黄金市场的用时较短,对黄金价格变化影响较大;而国际黄金价格的变动传染到原油市场则用时稍长,且对原油价格波动的影响相对较小。
作为一种基础性能源,原油对经济增长和社会发展起到至关重要的作用。而黄金作为贵金属中最受推崇的硬通货,它具有极强的保值增值功能,同时还被广泛地运用于高新技术产业之中。原油和黄金同属于大宗商品,是宏观经济的重要指标。因此,对于原油市场和贵金属市场之间的关系进行深入研究,有助于明确大宗商品市场的整体走势,把握重要战略资源的市场走向。
相关文献表明,原油与黄金的价格具有明显的同向运动趋势,并且这种趋势是长期存在的。如董杰等通过对WTI原油期现货、标准普尔500指数与黄金市场之间的关系进行实证研究,发现WTI原油与黄金市场之间的相关系数具有显著的时变特征,即两市场间呈现出了明显的动态相依关系〔1〕。李红霞等也得出了类似结论,他们利用2005年7月至2011年3月的交易数据,在一个框架下考察我国能源和金融市场的动态相关性,结果显示:黄金与原油之间呈现出正向关联关系,但只存在着从黄金对原油方面的单向均值溢出效应〔2〕。而林征等人的结论则更进一步,他们通过对原油、黄金和美元关系的研究发现,原油市场与黄金市场间存在着双向的波动溢出效应,价格波动信息可以互相传导〔3〕。
早期学者对原油和黄金价格关系的研究,通常是嵌套在多资产研究中,得出的结论也不全一致。在此基础上,我们还需要进一步对原油和黄金之间的风险传染关系进行深入研究,从强度和方向两个方面得出更全面的结论。在现代社会纷繁复杂的金融关系中,研究原油和黄金之间的风险传染关系,对掌握大宗商品价格走向关系,规避相应的价格风险具有重要意义。
而在以往的金融风险关系研究中,多数文献侧重基于EMH理论而展开,但在现实生活中,金融类资产收益率常常呈现出较明显的“尖峰、有偏、胖尾”等典型事实特征,基于EMH理论建立的模型一般难以有效地将这些特征捕捉,已有众多学者对此问题进行了阐述,如王久胜等、于文华等〔4~5〕,而Copula模型自身具备的特点却可以很好地解决此类问题。张凯等提出,Copula函数可以对金融类资产收益序列进行良好的非线性分布捕捉,为反映金融类资产之间的相依关系提供了一种新的思路,使对金融类资产组合之间的研究达到了一个新的高度,为研究不同市场间相依性关系的传递、影响和感染提供了一种新的研究方法〔6〕。
对于金融资产之间的风险传染关系的测度,如果仅是得到它们之间具有相关性,即风险依存关系并不全面,还可以进一步研究风险传染的方向,以及一个资产价格变化对另一个资产价格变化的贡献程度,向量自回归(Vector Auto Regression,VAR)模型可以解决这一问题。
现有文献表明,VAR模型不仅可以得到金融资产之间风险传染关系的方向,还可以得到在固定传染方向下,一种资产对另一种资产产生影响的持续时间和贡献度,如Cologni等以及Kilian等都得出了此类结论〔7~8〕。而且根据吴振信等的研究,VAR模型的设立是基本不依赖经济原理的,它主要依据变量自有的动态规律对其本身进行研究,以联立方程的形式,将系统中每一个内生变量作为所有内生变量的滞后值的函数来构造模型,以反映这些变量间的动态联系〔9〕。马轶群等也认为VAR模型是分析和预测多个具有相关性的经济指标的容易操作的模型之一,它也经常用于预测相互联系的时间序列系统,以及分析随机扰动对于整个变量系统的动态冲击〔10〕。
基于以上分析,本文选择WTI原油价格和伦敦黄金定盘价作为研究对象,同时运用Copula模型和VAR模型进行实证研究。相对于目前一些学者单一的使用Copula模型或VAR模型对国际原油和国际黄金价格的风险传染关系进行研究,同时使用这两种方法进行研究不仅能得到国际原油和国际黄金价格之间的风险依存强度,还能得到风险传染的方向,即可以同时得到定量和定性两个方面的结论。
一、模型选定
(一)t-Copula模型
为研究国际原油和国际黄金价格之间的风险依存关系,本文采用二元时变t-Copula模型进行具体分析。
根据Sklar定理,Copula函数是一个多元分布函数,其边缘分布为〔0,1〕上的均匀分布〔11〕。一个二元的Copula函数(简记为C)可以表示为:
C(u,v)=Pr(U≤u,V≤v),
令U=F(x),V=G(y),那么X和Y的联合分布函数可以表示为:
H(x,y)=C(F(x),G(y))。
其中,H(x,y)表示X和Y的联合分布函数,F(x)和G(y)则分别表示X和Y的边缘分布函数。从此定理可以看出,Copula函数可以表现变量之间的相关关系。
Copula函数具有许多优点。第一,它可以进行变量的边缘分布及其相关结构之间的独立研究,所以使用Copula连接功能构建多元金融模型更易于操作;第二,构建Copula连接模型,变量的边缘分布不需要同Copula模型的分布相同就可以直接操作;第三,如果对变量做了单调增变换,由Copula函数导出的相关测度值是不变的;第四,Copula函数可以捕捉变量间特殊的非线性的、非对称的相关关系,使研究结果更加符合实际情况〔12〕。
基于以上优点,Copula理论也得到了越来越多的重视,近年来被普遍运用于金融相关性分析、金融风险测量的研究当中。Copula族函数有很多种,其中运用较广的为二元时变t-Copula函数。二元时变t-Copula函数能比较敏感地对随机变量之间的尾部相关变化进行感应,在反映数据随时间变化、捕捉数据“尖峰,厚尾”等特征方面具有独特优势,如魏平等、于文华等在相关文献中皆得出了类似结论〔13~14〕。
对于二元时变t-Copula函数,设变量之间的线性相关系数为ρ,则自由度为d的二元时变t-Copula函数的条件概率密度函数的表达式为:
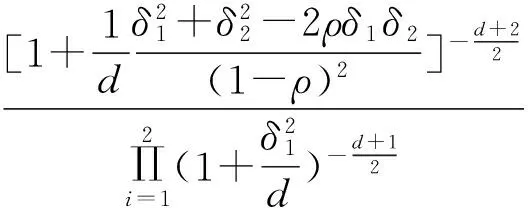

(二)VAR模型
本文引入VAR模型及其分析框架来考察某变量的冲击对另一变量的影响方向、强度和时间。
VAR模型是由2011年诺贝尔经济学奖获得者克里斯托弗·西姆斯(Christopher A. Sims)在1980年的时候创立并引入到经济学中的,它不是基于不确定理论给出的先验信息,而是从统计方法角度对模型施加约束,在不需要区分变量内生性和外生性的基础上,直接用真实数据对多个变量间动态关系进行描述〔16〕。在VAR模型的分析框架内,还可以运用格兰杰因果检验、脉冲响应函数和方差分解三种方法对变量间的动态关系进行进一步分析。
根据汪昌云等的研究〔17〕,对于含有k个时间序列的集合,一个VAR模型可以捕捉变量之间的动态影响,p阶基础模型VAR(p)模型的表达式为:
yt=μ+Φ1yt-1+…+Φpyt-p+ut,
t=1,2,…,T。
其中:p是滞后阶数,T是样本个数;μ是k×1维常数向量,Φ是待估计的k×k维自回归系数矩阵,ut是k×1维向量白噪音,且有ut~IID(0,Ω);另外,E(ut)=0,E(utyt-i)=0,也就是ut与内生变量yt及各滞后期不相关。在建立VAR模型之前,首先要确定模型的滞后阶数,保证最优滞后阶数才可以保证误差项为白噪声向量。
在得到VAR模型的基本参数之后,可以基本判定变量之间的动态影响关系,另外VAR模型建立之后需要对其进行识别检验,来判断其是否符合原设定和经济意义。所以在建立VAR模型的基础上,可以进行格兰杰因果检验,格兰杰因果检验可以用来检验其中一个变量的滞后项是否能够对另一个变量的当期值产生影响,所以格兰杰因果检验通常可以解释为,在VAR模型中,某一个变量的变化是不是可以用来对其他相关变量进行变化预测。
格兰杰因果关系的定义为:如果yt和xt的滞后项所决定yt的条件分布与仅由yt的滞后项决定的条件分布相同,即
F(yt|yt-1,yt-2,…xt-1…)=
f(yt|yt-1,yt-2,…),
则称x是y的非格兰杰原因;反之,则称x是y的格兰杰原因。
在得到变量对变量的影响方向之后,还可以继续分析当误差项发生变化或者说是模型受到某种风险冲击时对系统的动态影响,简单来说,就是比如yt在受到一个单位的随机扰动因素冲击后的动态变化路径,这种分析方法就是脉冲响应函数(IRF)。通过脉冲响应函数可以检验国际油价的变化及国际黄金价格的变化对对方的价格产生影响的强度和持续时间。
脉冲响应函数描述的是,VAR模型中的一个内生变量在受到冲击之后,给其它内生变量所带来的影响,而每一个结构冲击对内生变量产生影响的贡献度则需要方差分解来实现的。方差分解把系统中每一个内生变量的波动按其成因分解成各随机扰动项影响的总和,从而通过方差贡献度的大小,来衡量随机扰动项对变量的相对重要程度。在本文中,通过方差分解,可以确定国际油价变动及国际黄金价格变动在对方价格变化中的作用大小。
二、实证研究
(一)样本选择
本文选择美国西德克萨斯原油期货连续价格(WTI)作为国际原油价格的代表,选取英国伦敦黄金定盘价作为国际黄金价格的代表,对国际原油和黄金价格的关系进行研究,样本时间段为2000年1月4日到2013年6月6日,两组数据同为3218个,数据来源于美国能源信息署(EIA)和伦敦金银协会市场。为了方便进行分析说明,本文将西德克萨斯原油期货连续价格的收盘价简称为WTI,而将伦敦黄金定盘价简称为LDHJ。本文所用的软件主要是MATLABR2009b和EViews7.11,将WTI和LDHJ的每日价格记为Pt,并定义每个资产的每日收益率为Yt,Yt=Ln(Pt)-Ln(Pt-1),t=2,3,…,N,并将WTI价格序列的收益率序列简记为RWTI,LDHJ价格序列的收益率序列简记为RLDHJ。
(二)收益序列描述统计分析
表1是RWTI序列和RLDHJ序列的描述统计结果,从中可以看出:两个收益序列的偏度系数都在1%的显著性水平下显著,即两个收益序列的分布具有明显的有偏、尖峰特征;两个收益序列的J-B统计量也均在1%的显著性水平下拒绝了正态分布;运用ADF检验收益序列的平稳性,结果都明显拒绝了非平稳性假设;运用BDS检验收益序列是否服从独立同分布(I.I.D),结果表明它们明显拒绝I.I.D特征;运用Ljung-BoxQ统计量对收益序列进行自相关性检验,结果表明在滞后期为25时,两个收益序列都明显拒绝无自相关性;运用no ARCH检验收益序列是否存在ARCH效应,结果均拒绝无ARCH效应而表现出明显的异方差特征。

表1 RWTI和RLDHJ序列的描述统计特征
***代表在1%水平下显著,**代表在5%水平下显著。后同。
图1~图4是原油和黄金收益序列波动情况及波动分布与正态分布相比较的QQ图。从图1~图4中可以看出:收益序列波动图表明两个收益序列都明显存在波动聚集现象,即大波动之后是大波动,小波动之后是小波动的特征;QQ图表明两个收益序列的分布比正态分布有更长的尾部,也就是说如果假定收益序列服从正态分布进行研究并不能真正反映能源和贵金属市场的典型事实特征,也就无法对两个市场间的风险相依关系进行有效刻画。

图1 原油收益序列波动走势图
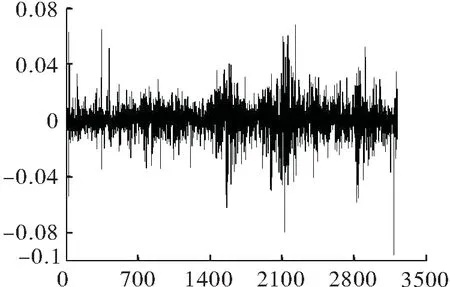
图2 黄金收益序列波动走势图

图3 原油收益序列分布VS正态分布的QQ图

图4 黄金收益序列分布VS正态分布的QQ图
在对数据进行基本的分析梳理后,针对收益序列具有的有偏、尖峰、自相关性、异方差性、厚尾、波动聚集等典型事实特征,可以选用AR(1)-GARCH(1,1)模型建立波动率模型,并获取它们的标准残差序列。ARCH模型一直被运用于金融经济时间序列的波动性研究,但该模型只适用于异方差函数短期自相关过程,而GARCH模型正好在此基础上又增加考虑了异方差函数的p阶自相关性,它对时间序列数据进行处理考虑的方面更周到。
本文选择的AR(1)-GARCH(1,1)模型的函数为:
Rt=η0+η1Rt-1+εt,
εt=φtZt,



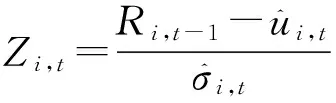
将WTI和LDHJ价格的收益序列经过AR(1)-GARCH(1,l)-t模型拟合后,对其标准残差序列进行检验后,发现收益序列的标准残差具有明显的“有偏,尖峰”特征,J-B统计量结果表明各标砖残差序列拒绝正态分布,LM检验结果表明各标准残差序列不再有异方差性,LBQ检验表明各标准残差序列不能拒绝无自相关假设,BDS检验结果表明各标准残差序列满足独立同分布的原假设不能被拒绝。
(三)风险依存关系的测度
在对WTI和LDHJ收益序列经过AR(1)-GARCH(1,l)-t模型拟合后,本文对其标准残差序列进行了相应的概率积分变换,并得到了它们各自的边缘分布,在此处上了构建了二元时变t-Copula模型,并得到了WTI和LDHJ的动态相依系数。图5显示了二元时变t-Copula模型拟合的WTI和LDHJ的动态相依系数的变化趋势图,由长期历史价格走势而得出的WTI和LDHJ的风险相依关系的强度均值为0.18。

图5 RWTI和RLDHJ序列的动态相依系数
从图5可以看出,WTI和LDHJ具有明显的风险相依关系,并且两者的相依性还表现出明显的时变特征,它比一般的线性相关系数更能反映在瞬息万变的金融、经济环境下,能源和贵金属的市场价格受到的多种因素的影响而表现出的动态风险相依关系。即在长期均衡中,可能先是WTI的价格波动后,传染带动了LDHJ的价格波动,也可能是LDHJ的价格先波动,后传染带动了WTI的价格波动,即风险传染在两者之中是明确存在的,还不能确定传染方向,需要通过进一步研究证明传染方向。
(四)风险传染方向的测度
在建立VAR模型的基础上,由格兰杰因果检验、脉冲响应函数和方差分解方法来得到WTI和LDHJ在自己产生变化后对另一变量的影响方向、强度和时间。
1.VAR和格兰杰因果关系检验
从表2可以看出,WTI和LDHJ价格的收益序列均已通过ADF单位根检验,说明两者都是平稳序列,本文根据LogL,LR,FPE,AIC,SC和HQ六大准的多数原则建立了WTI和LDHJ的VAR(6)模型,且此VAR(6)模型的所有根模均小于1并且都位于单位圆内,说明此模型满足稳定性条件,结果如表2所示。在WTI收益率方程中,LDHJ收益率滞后2阶的系数在1%的显著性水平下是显著的;在LDHJ收益率方程中,WTI收益率滞后1阶的系数在1%的显著性水平下是显著的,说明WTI原油市场和伦敦黄金市场之间不仅具有明显的风险依存的相关关系,还存在着经由价格进行传导的双向风险溢出效应,即WTI的价格变化会引致LDHJ的价格变化、LDHJ的价格变化也会引致WTI的价格变化,此结果与表3的格兰杰因果检验结果一致。

表2 VAR(6)模型

表3 格兰杰检验结果
2.脉冲响应函数
脉冲响应函数可以根据假设情景的需要来设定相应的冲击的强度与方向,它不但可以分析一个变量受到另一个变量的影响的大小、方向,而且还可以得到影响的时间框架。图6和图7是RWTI和RLDHJ的相互脉冲响应函数结果,图中实线表示脉冲响应函数,虚线表示正负两倍标准差偏离带。

图6 RLDHJ对RWTI的脉冲响应

图7 RWTI对RLDHJ的脉冲响应
从图6和图7中可以看出,在本期给WTI原油期货市场一个正冲击之后,伦敦黄金市场会在当期就直接达到最高点,然后会持续下降并在第3期达到最低点,之后会出现较小的波动上升和下降状态。还可以看出,在本期给伦敦黄金市场一个正冲击之后,WTI原油期货市场会波动上升,在第3期出现最高峰,之后会出现较大的波动下降和上升状态。由此表明,无论先是WTI原油期货市场先受到风险冲击,还是伦敦黄金市场先受到风险冲击,风险都会由它传染到另一个市场。
不同的是,WTI先受到风险冲击后,传染到伦敦黄金市场的用时较短,而伦敦黄金市场先受到风险冲击后,风险会延时传染到WTI原油期货市场。在原油市场与黄金期货市场交易信息的联动上,两个市场间的波动信息是可以相互反馈的,两市场的联系是异常紧密的。当原油价格变化的时候,比如价格下降,产油国为平衡国际收支逆差,会选择抛售大量的黄金储备,从而造成黄金价格的迅速下降。反之,当黄金价格变化的时候,比如价格上涨,就会吸引大量资金流入黄金市场,作为国际结算货币的美元的需求量就会增加,就会促使产油国为获取更多的美元而提高原油价格,此过程需要时间进行消化。
3.方差分解
通过方差分解可以看出,VAR模型的方差分解能够给出随机新息项的重要信息,表4和表5给出了利用蒙特卡洛模拟1000次方差分解的结果。

表4 WTI原油的方差分解结果

表5 伦敦黄金的方差分解结果
由表4和表5可以看出,WTI原油市场的冲击变化对伦敦黄金市场的变化的贡献度是高于伦敦黄金市场的冲击变化度对WTI原油市场的贡献度的,这与脉冲响应函数的结果是相对应的。相对于黄金在世界经济发展中起到的作用来说,原油资源作为工业生产领域最为基本的能源原材料,在世界经济发展中起着更为重要的作用,它的变化给其他行业、领域带来的影响都比较大。当原油价格变动幅度较大,会给实体经济带来巨大压力,进而影响到经济稳定和金融资产的价值,此时大多数人就会对价值比较稳定的黄金资产进行对应的操作,进而促使其价格变动。而黄金作为价值一直都比较稳定的投资品,它的价格变动更多地会影响到人们对金融资产的估值,而对于社会经济的影响相对较小,自然黄金对于原油价格的影响也就不及原油价格变动对黄金的影响。
经过VAR模型的系列结果来看,风险传染在WTI原油市场和伦敦黄金市场之间是双向存在的,相对来说,WTI原油市场先受到一定风险的冲击之后,对于伦敦黄金市场的影响持续的时间比较长,而且对其影响也比较大。
三、结论及政策建议
本文选择美国西德克萨斯原油期货(WTI)价格和伦敦黄金定盘价(LDHJ)作为国际原油和国际黄金市场的代表进行了研究,研究结论如下:
第一,本文选择能够显著捕捉金融资产收益率典型事实特征的二元时变t-Copula模型对WTI和和LDHJ的风险相依关系进行分析。通过研究,发现WTI和LDHJ之间确实存在着风险相依关系,并且是具有跟随市场变化而起伏的时变风险相依关系,比较具体形象地对两者之间的风险相依关系进行了描述,更能反映出能源和贵金属价格受到多种因素影响而表现出的动态风险相依关系。
第二,为了得到WTI和LDHJ的风险传染方向,本文又建立了VAR(6)模型,还在此基础上建立了脉冲响应函数和方差分解方程,并得到了双方风险溢出关系的持续时间和贡献度。相关结果表明,风险由原油市场再传染到黄金市场的时间较短,对于黄金市场价格波动的贡献度较大;而风险由黄金市场传染到原油市场的时间则稍长,而且对原油市场价格波动的贡献度较小。
基于实证研究的结论,本文提出以下建议:
第一,原油价格变动会给一国经济带来重要影响。油价上涨虽有利于国内石油化工企业发展,但会增加我国经济建设成本,增大居民生活压力,不利于我国经济稳定发展;油价下降会降低我国经济建设成本,降低居民生活压力,但是却有损于油化工企业的发展。因此,对于国际油价的变化,我们要时刻关注,以防油价大幅变动影响到国家经济建设。
第二,黄金作为升值空间巨大的稀有资源,越来越受到投资者的青睐,流通于黄金市场的资金也日益增加。但是,如果黄金价格变动浮动过大,会引起成投资者过度恐慌,不利于黄金市场的稳定发展。所以,我们必须关注国际黄金价格的变化,规避价格风险。
第三,原油和黄金作为对一国经济具有重要作用的大宗商品资源,一旦一方出现剧烈的价格波动,另一方就会连带发生类似现象,从而不利于一国社会稳定和经济发展。有关部门在监测石油和黄金价格会产生的风险时,要注意将两者结合起来,以达到全面预防、控制的目的。
第四,投资者在进行投资时,可以选择黄金或原油与其他类金融资产组合来规避风险。因为,投资者若同时投资这两类资产,虽然可以有机会得到两者同时暴涨而带来丰厚的收益,但是却更可能会遇到两者同时暴跌,给自己带来巨大损失。
目前我国还有没有原油期货,但是国内有关部门正在逐步落实原油期货的推出工作。在政府推出原油期货后,要注意防范原油期货和黄金期货会产生的风险传染关系,做到未雨绸缪。
参考文献:
〔1〕董杰,潘和平,姚一永,李成刚.基于DCC-MVGARCH模型的石油、股票和黄金市场相关性实证研究〔J〕.预测,2012,31(4):53-57.
〔2〕李红霞,傅强.我国实物资产与金融资产市场的动态相关性研究——基于五元VAR-DCC-MVGARCH模型的系统检验〔J〕.预测,2012,31(2):7-17.
〔3〕林征,林雅娜,黄晓玲.黄金、美元、石油市场间溢出效应研究——基于3元 BEKK-GARCH模型的实证分析〔J〕.经济研究导刊,2015,(11):196-199.
〔4〕王久胜,包卫军,胡杰.基于多维Gumbel Copula函数的投资组合VaR分析〔J〕.数理统计与管理,2010,29(1):137-143.
〔5〕于文华,魏宇,岳焱.次贷危机对亚洲股市尾部极值风险传导的影响研究〔J〕.预测,2013,32(3):3-18.
〔6〕张凯,魏子凯.基于Copula函数尾部相关性的股票交易策略〔J〕.统计与决策,2014,(16):56-58.
〔7〕Cologni A,Manera M.OilPrices,InflationandInterestRatesinaStructuralCointegratedVARModelfortheG-7Countries〔J〕.Energy Economics,2008,30(3):856-888.
〔8〕Kilian L,Park C.TheImpactofOilPriceShocksOntheUSStockMarket〔J〕.International Economic Review,2009,50(4):1267-1287.
〔9〕吴振信,薛冰,王书平.基于VAR模型的油价波动对我国经济影响分析〔J〕.中国管理科学,2011,19(1):21-28.
〔10〕马轶群,史安娜.金融发展对中国经济增长质量的影响研究——基于VAR模型的实证分析〔J〕.国际金融研究,2012,(11):30-39.
〔11〕Nelsen R B.AnIntroductiontoCopulas〔M〕.Springer,NewYork,1999:18,90-95,125-137.
〔12〕李秀敏,史道济.金融市场组合风险的相关性研究〔J〕.系统工程理论与实践,2007,(2):112-117.
〔13〕魏平,刘海生.Copula模型在沪深股市相关性研究中的应用〔J〕.数理统计与管理,2010,29(5):890-898.
〔14〕于文华,魏宇,康明惠.不同时变Copula-EVT-ES模型精度比较研究〔J〕.管理科学学报,2015,18(15):32-45.
〔15〕Engle R.DynamicConditionalCorrelation-ASimpleClassofMultivariateGARCHModels〔J〕.Journal of Business and Economic Statistics,2002,20(3):339-350.
〔16〕吕光明,徐曼.中国的短期国际资本流动——基于月度VAR模型的三重动因解析〔J〕.国际金融研究,2012,(4):61-68.
〔17〕汪昌云,戴稳胜,张成思.基于EVIEWS的计量经济学〔M〕.中国人民大学出版社,2011:72-124.
(责任编辑:叶光雄)
Study on the Risk Contagion Relationship between the International Crude Oil Price and Gold Price
ZAHNG Qing-duo1, YANG Kun1, XIONG Xue-wen2
(1.CommercialCollege,ChengduUniversityofTechnology,Chengdu610059,China;2.SchoolofEconomicsandManagement,ChongqingUniversityofArtsandSciences,Chongqing402100,China)
Key words:international crude oil; international gold; commodity markets; risk dependence; risk contagion; spillover effect; financial risk
Abstract:We took WTI and London gold price as the research objects, constructed copula model to get the risk-dependent intensity between them, and used the VAR model to discuss direction of the risk contagion. The results show that there exists obvious dynamic dependency relationship and bidirectional risk spillover effects between international crude oil and gold prices. The influence of the change of international crude oil price on the gold market is relatively shorter and the fluctuation of gold price is greater, while effects of international gold price changes on the oil market are slightly longer, and the fluctuation of crude oil prices is relatively small.
收稿日期:2015-12-06
基金项目:教育部人文社会科学基金项目(15YJA630076);四川省教育厅人文社会科学重点项目(14SA0039);四川省科技青年基金项目(2015JQO010);四川省科技创新苗子工程资助项目(2014-018);四川省大学生创新创业训练计划项目(201510616061);成都理工大学中青年骨干教师培养计划资助项目(JXGG201420)
作者简介:张清朵(1990-),女,河南南阳人。硕士研究生,主要从事金融市场与风险管理研究。E-mail:342740119@qq.com。
中图分类号:F830.93
文献标志码:A
文章编号:1009-4474(2016)02-0103-08
