基于学习环模式的量子力学教学模式研究

李宗宝+王应+李勇

【摘要】作为当前公认的比较有效的教学模式，通过实践证明，学习环模式对于提高理工科专业授课效率具有重要的意义。结合教学实际，本文以物理学专业课《量子力学》中的“一维无限深势阱”内容为例，设计了教学案例，介绍了学习环模式在物理学专业课程教学中的应用。

【关键词】学习环模式 量子力学 一维无限深势阱

【中图分类号】G642 【文献标识码】A 【文章编号】2095-3089（2016）05-0043-02

学习环模式是20世纪50年代末60年代初，由美国的一项关于小学科学课程的项目——科学课程改善研究（science curriculum improvement study，简称SCIS）首次提出的一种科学的教学策略[1，2]。以皮亚杰的发生认识论为基础，借鉴和运用构建主义学习理论。经过西方近半个世纪的教育实践，该方法已经由小学科学课程提出，现被大学理工科专业课程的教学所借鉴[3]。虽然针对不同的课程，其研究者对学习和教学过程研究的重点不同而不断变化学习环的方式，但他们都具有一些共同的特征环节，即：探究或实验、解释或发明、巩固或精致，这三个主要部分[4，5]。

作为物理学专业的必修专业课程，量子力学课程，由于其理论性极强等特点[6-8]，需要扎实的数学和物理知识，且由于其知识抽象、较难理解等造成学生的学习兴趣不高、知识掌握程度不够。因此急需在当前授课模式下，对量子力学的授课方式进行改革，以此提高学生学习的积极性。将学习环模式应用到物理学专业量子力学的教学中，在于利用学习环的探究性特点，造成学生对知识点的饥渴，从而充分调动学生学习的主动性，以此提高学习效率。同时，学习环模式亦将所学知识与学生的学习生活相融合而更好地发挥作用，提高学生学习的积极性。

本文以物理学专业《量子力学》中的“一维无限深势阱”为例，阐述学习环模式在物理学专业学生授课中的应用。

一、探索阶段

通过对所授知识点与科技前沿的联系，对课程进行情景设计，在情景中提出问题，从而激发学生的探索欲。在问题的提出中，需要侧重注重该问题应该为依靠学生目前所掌握的知识是无法解决的，并且是在原有知识体系的基础上学习新知识才能解决的。通过问题的提出，使学生发生对未知知识点的心理失衡，从而发生认知冲突，激发学生探究的兴趣和好奇心，进而将学生的注意力吸引到学习任务中来。同时，问题的提出亦应具备新颖性和趣味性并存，尤其科技前沿知识最佳，其能够在克服课本中知识的枯燥性的同时开拓学生视野。

针对量子力学中一维无限深势阱知识点，在课程布局中，首先，通过PPT展示出与之相对应的科技前沿知识——碳纳米管，如图1所示。并结合碳纳米管在催化剂、储氢等方面的应用，并结合我国及世界目前对碳纳米管的研究现状展开论述。在此基础上，就其储氢方面的应用于木桶模型（b）进行对比，并提出问题：（1）碳纳米管的储氢量多少与什么因素有关？（2）木桶的储水量由最低板决定，是否碳纳米管亦与之类似？（3）氢原子或氢分子在碳纳米管中的存在状态是如何？（4）如何讨论氢原子在碳纳米管中的状态分布？在这样的情景中学生就会随着授课老师的思路进行相应的思考，这时学生的好奇就得以放大，学习兴趣大增，而课程亦会随着预先设定好的问题的不断解决而顺利推进。从而消除普通授课模式中单纯知识点讲解的枯燥性。

在这一阶段中，授课教师作为课堂的主要引导者，其主要任务是构建合适的情景，适当引导学生思考，给学生一定的思考和想象空间。当然，为使学生学习兴趣有持续性，此时教师的指导不能太多，更不能直接将答案告诉他们。此处引导不当则将很难达到预期效果。

二、概念介绍

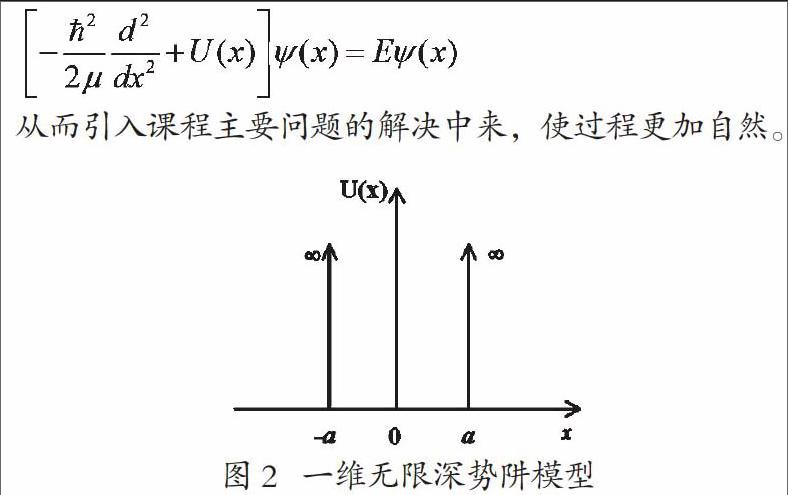
在前面探索的基础上，提出解决氢原子在碳纳米管中的求解方式。而此处可以较为容易的通过碳纳米管及氢原子构建物理模型。由于碳纳米管的对称性，在简化其三维构型的基础上，提出在一维方向上的模型；对于氢原子，则忽略其离子大小，假设为自由离子模型，从而构建出如图2所示的结构模型。在此模型基础上，引用前节知识点——薛定谔方程对自由离子的运动状态进行公式的构建，容易得到该条件下的薛定谔方程：

从而引入课程主要问题的解决中来，使过程更加自然。

在知识点的讲解与模型的构建及解的过程中，需要较多的运用数学知识，因此会显得枯燥乏味。此时需要更多的引导学生，让学生结合前述知识点自然引入，从而加深学生对旧知识的巩固和对新知识的印象。

通过对一维无限深势阱中薛定谔方程的探究，可以结合探索阶段提出的氢原子在碳纳米管内的存储问题，让学生思考理解该问题的解决过程与一维无限深势阱中模型计算结果之间的区别与联系，并探究出现该问题的原因？在该问题的基础上，对学生进行分组讨论模型与实际问题之间的区别，以及在该问题基础上针对实际问题，前沿课题中对于实际问题的修正计算原理及方法，以此增加学生对于前沿课题的了解。

三、概念应用

在前述问题的基础上，通过探究性前沿课题问题的提出以及对一维无限深势阱中所牵扯到的薛定谔方程的求解，该阶段的任务是引导学生将发展出来的新概念应用于新情景，解答相关问题，加强学生对所学新概念的理解。在此基础上通过对一维无限深势阱进行边界条件的延伸，通过修改边界条件自然过渡至势垒贯穿章节。通过修改薛定谔方程中的势场U的条件，探究出射离子数量与势垒宽度之间的关系，并在此基础上引出势垒概念，并拓展其在实际中的应用——电子扫描显微镜的制造原理及实际应用。这一例题其实是在探索阶段所提出的问题基础上的探究，通过其分析让学生了解理论知识到实践之间的转化思路，扩展学生理论与应用之间的转化思路，培养学生的实践能力。

四、结论

通过对知识点中各个换件的设计，在整个学习环过程中，学生在心理上对于知识点必将经历一个“平衡-失衡-再平衡”的过程，其知识体系会原来的旧的知识体系达到新的更高知识层测体系，呈现出螺旋上升的特点。通过大量的实践，证明该学习环模式在大学物理学专业量子力学课程体系的教学中具有较好的推动作用。利用学习环模式，能够加强理论与实践的融合，推行基于问题、基于项目、基于案例的教学方法和学习方法。

参考文献：

[1]郑永爱.论科学教育学习环模式的涵义和发展[J].内蒙古师范大学学报（教育科学版），2005（6）：33-35.

[2]代鸣，姚宝骏.5E学习环教学模式在生物学教学中的运用[J].生物学教学，2008，7（33）：18-19.

[3]袁维新，吴庆麟.关于学习环模式的研究综述[J].心理科学，2007，30（3）：632-635.

[4]袁维新，吴庆麟.关于学习环模式的研究综述[J].心理科学，2007（3）：632-635.

[5]宋景芬.从归纳到演绎——元认知学习环教学模式及案例分析[J].教育实践与研究（中学版），2008（11）：53-55.

[6]李嘉慧.大学物理中的量子力学教学研究[D].大连理工大学，2012.

[7]田光善.关于本科生量子力学教学的一些体会[J].大学物理，2011，（3）：52-58.

[8]金桂，黄小益，蒋纯志，陈亚琦.量子力学教学方法探索与实践[J].高等理科教育，2011（2）：100-103.

基金资助：铜仁学院教学内容与课程体系改革重点与培育项目（《物理专业光学、原子物理学和量子力学一体化教学模式研究（重点）》）资助。