基于分数低阶类相关熵的双基地MIMO雷达目标参数联合估计新算法

李丽，邱天爽，贺明妍

（1.大连大学信息工程学院，辽宁 大连 116622；2.大连理工大学电子信息与电气工程学部，辽宁 大连 116024）

基于分数低阶类相关熵的双基地MIMO雷达目标参数联合估计新算法

李丽1，邱天爽2，贺明妍1

（1.大连大学信息工程学院，辽宁 大连 116622；2.大连理工大学电子信息与电气工程学部，辽宁 大连 116024）

针对Alpha稳定分布噪声环境下参数估计性能退化的问题，受类相关熵概念的启发，提出分数低阶类相关熵（FCAS）的概念，并采用分数低阶类相关熵准则对平行因子分析(PARAFAC)算法中基于三线性最小二乘（TALS）迭代准则的目标函数进行了修正，推导出适用于冲激噪声环境的韧性平行因子分析（FCAS-PARAFAC）算法，并将该方法应用于双基地MIMO雷达系统中目标参数估计中。FCAS-PARAFAC算法能够抑制脉冲噪声的影响，具有较好的估计性能，并且能够实现自动配对，仿真实验验证了算法的有效性。

双基地MIMO雷达；参数估计；分数低阶类相关熵；平行因子分析；Alpha稳定分布

1 引言

双基地MIMO（multiple-input multiple-output）雷达是将MIMO技术与双基地雷达技术相结合的一种新体制雷达。它避开了双基地固有的三大同步难题，在目标跟踪和检测、目标参数估计和目标成像等方面具有明显的优势，是雷达领域的一个研究热点。其中，相干MIMO雷达、发射阵列和接收阵列的各个阵元间距较小且集中放置，发射阵元发射相互正交信号，同时所有的发射接收天线对具有相同的目标雷达散射面积（RCS,radar cross section）值，从而受到更多学者的关注。本文主要研究双基地相干MIMO雷达的参数估计问题[1,2]。

目标参数估计和定位已成为雷达信号处理的一个研究的热点问题。目前，大部分学者在研究双基地MIMO雷达目标参数估计算法时都是在假设噪声环境为高斯白噪声的前提下进行的[3～7]，其中，张剑云等[6]基于平行因子分析理论，从三线性最小二乘迭代得到的矩阵中完成参数估计。然而该算法仅在高斯白噪声环境下具有较好的估计性能，对冲激噪声非常敏感，使算法的性能在冲激噪声环境下急剧退化。

在无线通信、雷达、水声和生物医学信号处理等实际应用中遇到的信号和噪声，许多是具有显著脉冲性的非高斯过程。对于这些信号和噪声，如果仍然采用高斯模型来描述，并基于二阶矩方法进行信号处理，则不能得到满意的结果。Alpha稳定分布是描述上述随机过程的最有潜力和最具吸引力的模型之一[8～10]。

相关熵作为一种随机变量局部相似性的度量，近年来受到广泛关注[11,12]。受相关熵理论及已有文献的启发，本文提出了分数低阶类相关熵(FCAS,fractional lower-order correntropy-analogous statistics)的概念，并采用分数低阶类相关熵准则修正平行因子分析算法（PARAFAC）中基于交替三线性最小二乘准则(TALS,trilinear alternating least squares regression)的目标函数，使之适用于冲激噪声环境，推导出基于FCAS准则的PARAFAC算法（FCAS-PARAFAC），并将该算法应用到双基地MIMO雷达目标参数估计中，实现了目标参数的联合估计，并能够自动配对。仿真实验表明，相对于TALS-PARAFAC算法，本文提出的新算法在冲激噪声环境下表现出很好的稳健性。

2 信号模型

双基地MIMO雷达系统如图1所示。发射阵元和接收阵元数目分别为M和N，阵元间距分别为dt和dr，在相同距离分辨单元上存在P个目标，(φi,θi)表示第i个目标所对应的雷达发射角（DOD,direction of departure）和接收角（DOA,direction of arrival）[6]。在一个发射脉冲周期内，目标的散射截面积（RCS）保持不变，而脉冲与脉冲间的起伏是统计独立的，并且不同目标的RCS波动是不相关的。各发射阵元同时发射相互正交的相位编码信号，若第m个阵元发射的第l个脉冲为

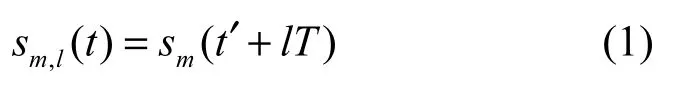
其中，t和t′分别对应慢时间和快时间，T表示脉冲重复周期。sm(t)为第m个发射阵元的基带波形。则第n个接收阵元接收的第l个回波脉冲为

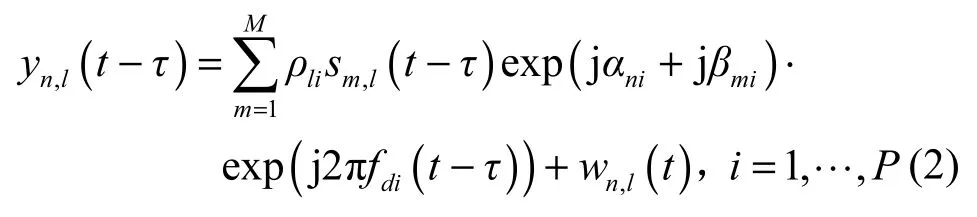
其中，n=1,…,N，l=1,…,L，τ为目标的回波延时，wn,l(t)为标准SαS稳定分布噪声。ρli为第l个发射脉冲在第i个目标上的散射系数。分别是接收导向量和发射导向量。fdi为第i个目标的多普勒频率。

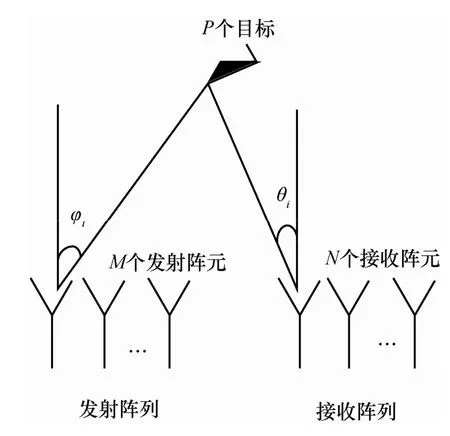
图1 双基地MIMO雷达阵列模型

由式(3)可以得到在P个目标情况下，L个回波的滤波器输出为

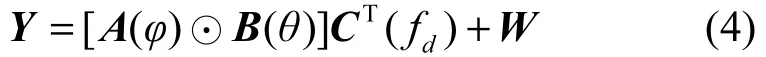
其中，Y=[η1,η2,…,ηL]为MN×L维的输出矩阵[6]。为P×L维的矩阵，它是多普勒频率的函数（假设目标的散射系数为已知），W为SαS稳定分布噪声。由式(4)可知，对MIMO雷达的发射角、接收角及多普勒频率的估计可转化为对A(φ)、B(θ)和C(fd)这3个矩阵的估计。

3 类相关熵与分数低阶类相关熵

3.1 类相关熵

设X与Y为服从独立同分布的对称Alpha稳定分布（SαS）随机变量，其特征指数满足1＜α≤2。对于2个随机变量X与Y，其类相关熵统计量（correntropy-analogous statistics）定义为

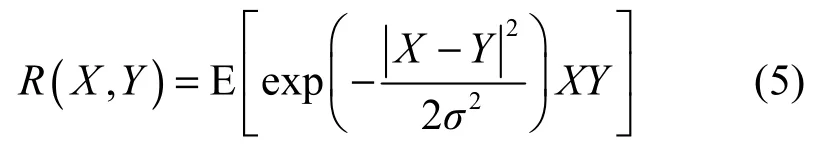
3.2 Alpha稳定分布

由于一个特征指数为α(α≤2)的稳定分布过程只存在有限的小于特征指数α的矩，因此，许多传统参数估计算法在稳定分布脉冲噪声条件下性能退化严重。Alpha稳定分布（Alpha-stable distribution）常简称为“稳定分布”，是描述上述随机过程的最有潜力和最具吸引力的模型之一。

如果存在参数0＜α≤2,γ≥0,−1≤β≤1和实数a使其特征函数具有式(6)的形式，则随机变量X服从稳定分布。

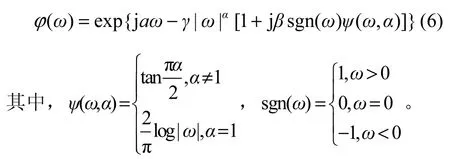
α为特征指数，它决定该分布脉冲特性的程度。α值越小，所对应分布的拖尾越厚，因此脉冲特性越显著。相反，随着α值变大，所对应分布的拖尾变薄，且脉冲特性减弱。当α=2时，为高斯分布，是α稳定分布的一个特例。γ＞0为分散系数，−1＜β＜1称为对称参数，a称为位置参数。

分数低阶统计量（FLOS,fractional lower-order statistics）是研究Alpha稳定分布环境下最基本的理论。对于满足0＜α≤2的联合SαS分布的随机变量X和Y，其位置参数a=0，则X和Y的p阶分数低阶相关定义为

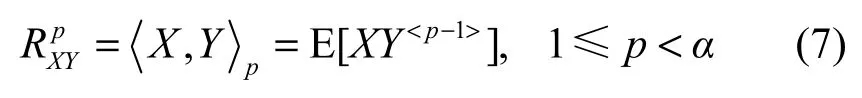
3.3 分数低阶类相关熵

由式(5)可以发现，当X=Y时，类相关熵为

根据SαS分布的性质可知，随机变量X与Y不具有有限的二阶矩。因此，在脉冲噪声环境下，该算法性能必然出现下降。受分数低阶矩理论启发，本文提出了分数低阶类相关熵（FCAS,fractional lower-order correntropy-analogous statistics）概念，其定义式为

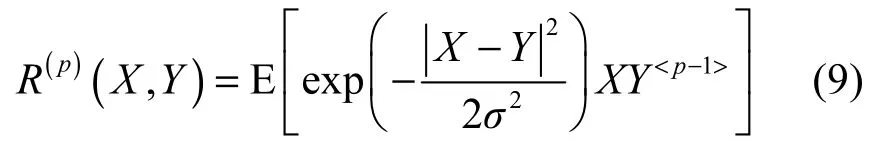
从分数低阶类相关熵的定义可以看出，R(p)(X,Y)中既包含了高斯核函数，对具有大幅度冲激的非高斯噪声具有较好的抑制作用，同时应用分数低阶矩理论，能更好地抑制冲激噪声的影响。

4 基于FCAS准则的平行因子分析算法

平行因子分析首先被提出是作为生理学中的数据分析工具，主要用于化学计量学、光谱学和色谱学等，是多维数据分析的一种方法。近年来，在信号处理和通信领域，平行因子技术被广泛关注[13,14]。PARAFAC是一种三维矩阵处理方法，在满足Kruskal条件下平行因子模型具有唯一可辨识性，可以在一次矩阵分解中得到含有目标参数信息的矩阵，使参数能够自动配对。

4.1 TALS-PARAFAC算法

平行因子分析模型通常采用交替三线性最小二乘回归TALS方法完成。匹配滤波器的输出具有三面阵模型特性，因此，它可以用Y沿接收方向、发射方向和快拍方向上的切片集合Y1、Y2、Y3来表示。

在文献[6]中，根据三面阵Y1、Y2、Y3估计矩阵A(φ)、B(θ)和C(fd)，通常采用三线性交替最小二乘方法（TALS）完成。TALS是三面阵模型数据检测的一种常用方法，其基本思想是在获得一组初始估计值后，每一步更新一个估计矩阵，更新的方法为：以此步中待更新的矩阵作为变量，其他矩阵依据上一次的估计结果作为常量，利用最小二乘法来更新。待更新完所有估计矩阵后，再进行下一次迭代，直到算法收敛为止。

众所周知，最小二乘算法是基于二阶统计量的，而脉冲噪声不存在有限的二阶矩，因此，在冲激噪声环境下采用最小二乘法进行迭代的参数估计方法性能退化甚至失效。

4.2 FCAS-PARAFAC算法

为了改善冲激噪声环境中TALS-PARAFAC算法的参数估计性能，本文采用分数低阶类相关熵准则对算法中的迭代的代价函数进行改进，提出了基于FCAS准则的PARAFAC算法，并将该算法应用到双基地MIMO雷达目标参数估计中。

具体的步骤如下。

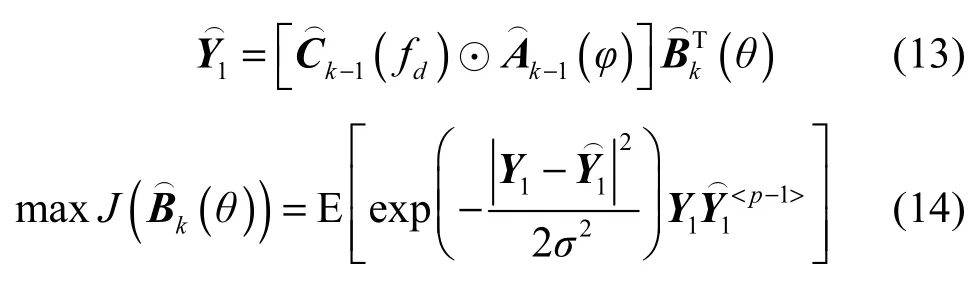
因此，

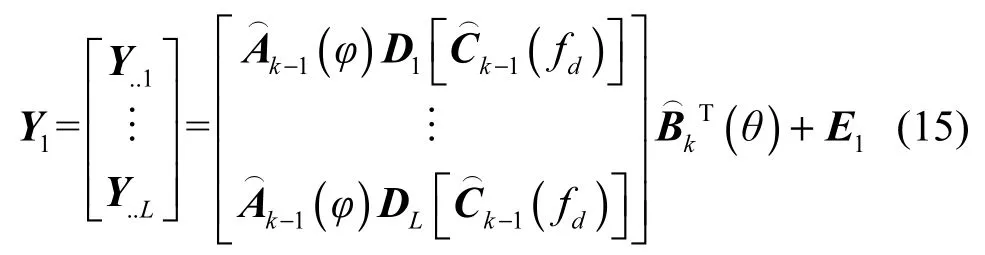
其中，E1为误差。当误差最小时，得到

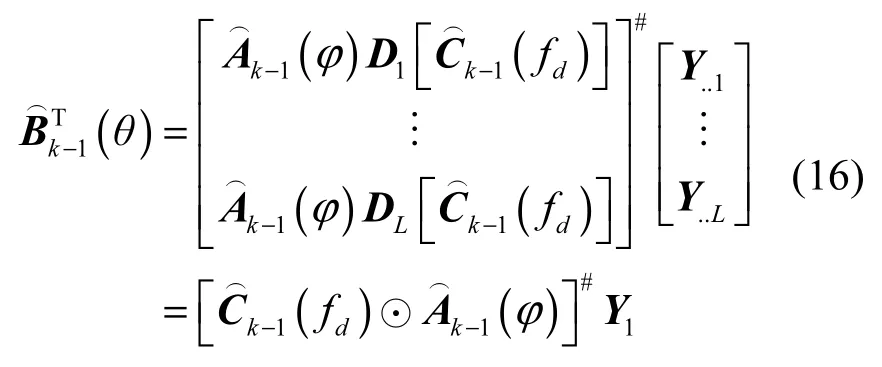
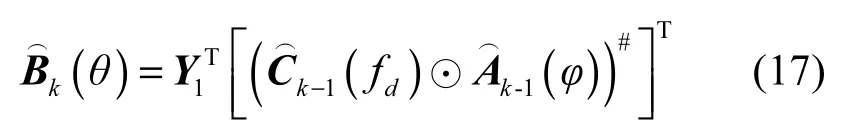
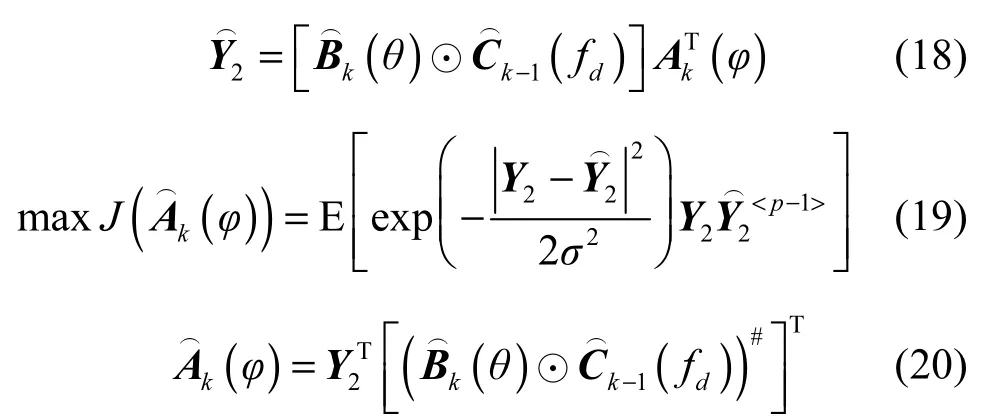
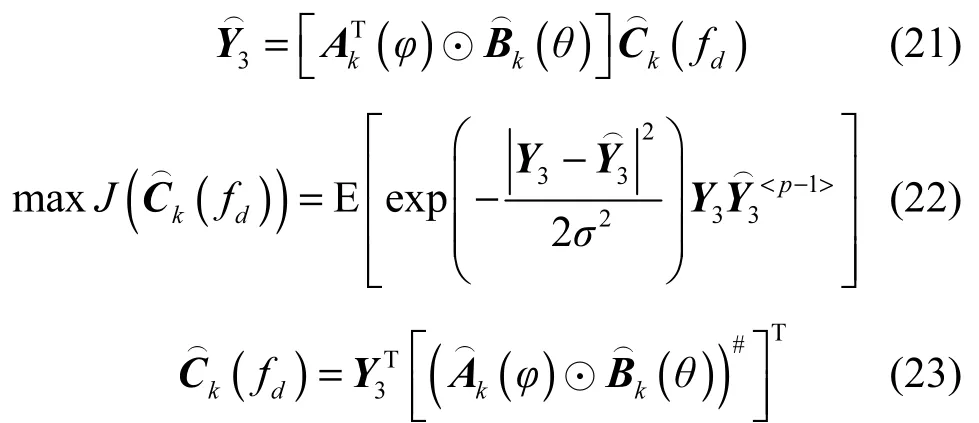
5) 经过上述迭代计算，得到A(φ)、B(θ)和 C(fd)的最终估计值，并令分别为3个估计矩阵的第j行第i列元素，通过式(24)～式(26)对各列向量求平均的方法得到，i=1,…,P。angle(·)表示取元素的相角运算。

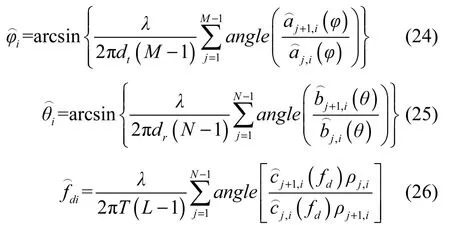
4.3 计算复杂度分析

本文算法和文献[6]算法都是对一组M×N×L的立体数据进行处理。由于上面的算法步骤可知，PARAFAC算法的运算量主要集中在迭代计算上，本文算法和文献[6]算法的迭代准则的计算复杂度相当。对于上述的三面阵的低秩分解，最大平均约需10次迭代即可完成，因此，本文算法的时间复杂度约为O(10(P3+LMNP))。其中，M为发射阵元数目，N为接收阵元数目，L为快拍数，P为目标个数。

仿真实验中，将本文算法与FLOS-FPSD算法[15]和TALS-PARAFAC算法进行比较，从时间复杂度分析文献[15]的性能，该算法主要集中在基于分数低阶统计量的分数阶功率谱的计算、谱峰搜索、MUSIC算法和ESPRIT算法的计算上，因此，该算法的时间复杂度约为O(PQ2lbQ+2N3+JNL+2M3)，其中，J为谱的数目，Q为信号采样点数目。因此，可以看出本文算法的时间复杂度明显低于FLOSFPSD算法。

5 仿真实验

假定发射阵元和接收阵元数目分别为M=6和N=8，双基地MIMO雷达远场存在2个目标，即P=2，相对于发射阵元和接收阵元的发射角和接收角分别为(ϕ1,θ1)=(20°,30°)和(ϕ2,θ2)=(50°,60°)，多普勒频率参数fd1=100 Hz ，fd2=160 Hz ，回波个数L=100。各发射阵元发射相互正交的Hadamard编码信号，且每个重复周期内的相位编码个数Q=256。本节使用广义信噪比（GSNR,generalized signal-to-noise ratio）作为信号和Alpha稳定分布噪声的度量。广义信噪比的定义式为

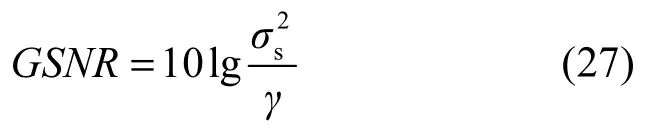
实验1在本节实验中，假定冲激噪声的特征指数α=1.4，0≤GSNR≤30。图2给出本文算法与TALS-PARAFAC算法及FLOS-FPSD算法参数估计的均方根误差随GSNR变化曲线。

从图2可以看出，FCAS-PARAFAC算法的性能优于TALS-PARAFAC算法和FLOS-FPSD算法。这是因为在Alpha稳定分布噪声环境下，不存在有限的二阶矩，所以基于二阶统计量的最小二乘算法性能退化。FLOS-FPSD算法基于分数低阶功率谱的谱峰搜索，再根据谱峰构造时频矩阵对收发角进行估计，因此，当信噪比较低时，信号被噪声淹没，不能得到正确的峰值点，在信噪比较低时具有较大的估计误差。谱峰搜索的误差会对后续收发角估计产生一定的影响；在构造时频矩阵估计角度前该算法需要2次峰值点搜索，因此具有较高的时间复杂度。FCAS-PARAFAC算法采用分数低阶类相关熵作为代价函数，其中，高斯函数和分数低阶统计量均具有较好的抑制脉冲噪声能力，因此具有较好的估计性能。

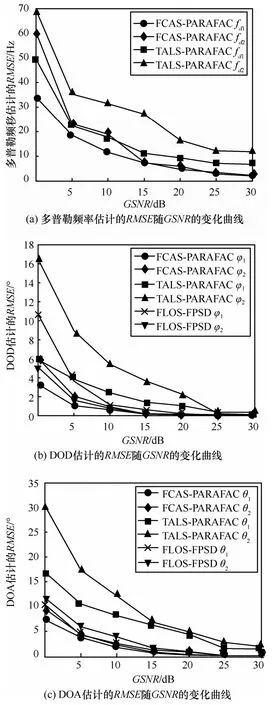
图2 3种算法参数估计RMSE随GSNR变化曲线

实验2研究了参数估计性能与冲激噪声特征指数α的关系。本节中参数设定为，GSNR=15dB ，冲激噪声的特征指数α的变化范围是1≤α≤2。图3给出了3种算法参数估计的RMSE与噪声特征指数α的关系。

图3 3种算法参数估计RMSE随噪声特征指数α变化曲线

由于Alpha稳定分布噪声的特征指数α越小噪声的冲激性越强，从图3可以看出，FCASPARAFAC算法具有较好的性能。TALS-PARAFAC算法不能很好地抑制冲激噪声的干扰，所以当α较小时，算法性能较差，当α=2时，冲激噪声转化为高斯噪声，所以当α接近2时，算法的参数估计的均方根误差变小。可见TALS-PARAFAC算法对冲激噪声比较敏感，在冲激噪声的环境下该算法的参数估计性能比较差。因此，由图2和图3可以看出，在冲激噪声环境下FCAS-PARAFAC算法的参数估计性能优于其他算法。

实验3研究了参数估计的准确率与广义信噪比GSNR及特征指数α的关系。参数估计的准确率可定义为，其中，D为真实值，为估计值。当多个目标时aP为多个目标参数估计准确率的平均值，本文为2个目标准确率的平均值。图4显示了参数估计的准确率随GSNR的变化曲线。图5显示了参数估计的准确率随噪声特征指数α的变化曲线。

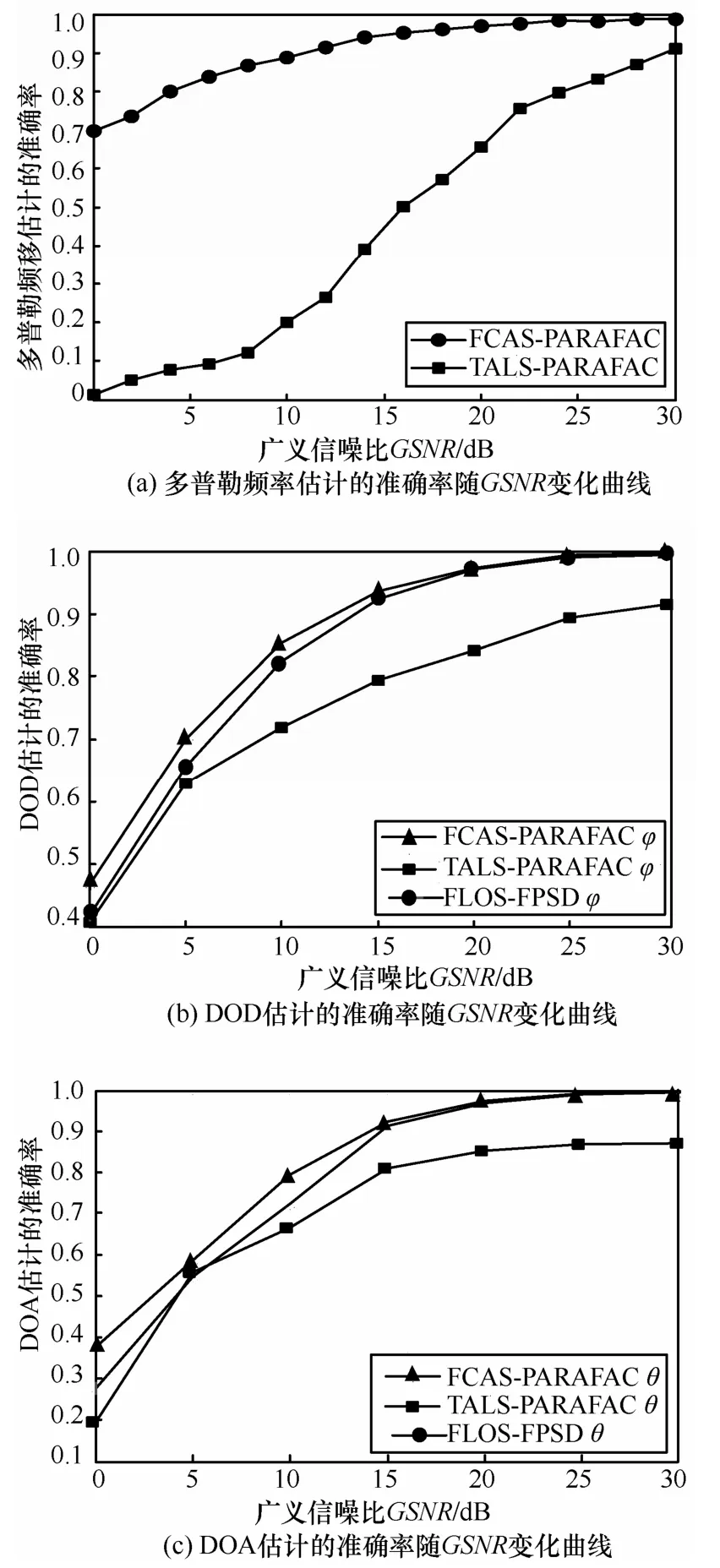
图4 参数估计准确率随GSNR的变化曲线

由于FCAS-PARAFAC算法考虑了冲激噪声的影响，采用分数低阶类相关熵准则最为代价函数进行迭代。而TALS-PARAFAC算法是基于二阶矩的，Alpha稳定分布噪声不存在有限的二阶矩，因此，TALSPARAFAC算法在稳定分布噪声环境下性能会显著退化。从图4和图5可以看出FCAS-PARAFAC算法相对于TALS-PARAFAC算法和FLOS-FPSD算法具有较高的准确率。

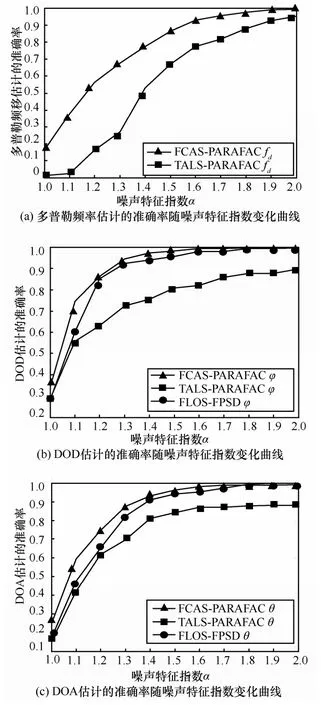
图5 参数估计准确率随噪声特征指数α的变化曲线

6 结束语

本文采用分数低阶类相关熵准则改进PARAFAC算法中基于TALS准则的代价函数，推导了适用于Alpha稳定分布噪声环境下的双基地MIMO雷达目标参数联合估计新算法。本算法不仅能有效地抑制稳定分布噪声的干扰，具有较好的估计精度，而且能够实现自动配对。仿真实验表明，在冲激噪声和高斯噪声环境下，与其他算法相比，FCAS-PARAFAC算法均具有很好的参数估计性能，尤其对突变的信号环境体现出更好的适应性。

[1]FISHLER E,HAIMOVICH A,BLUM R,et al.MIMO radar:an ideawhose time has come in[C]//IEEE Radar Conference.Newark,NJ,USA,2004:71-78.

[2]陈浩文,黎湘,庄钊文.一种新兴的雷达体制—MIMO雷达[J].电子学报,2012,40(6):1190-1198.CHEN H W,LI X,ZHUANG Z W.Arising radar system-MIMO radar[J].Acta Electronica Sinica,2012,40(6):1190-1198.

[3]谢荣,刘铮.基于多项式求根的双基地MIMO雷达多目标定位方法[J].电子与信息学报,2010,32(9):2197-2220.XIE R,LIU Z.Multi-target localization based on polynomial rooting for bistatic MIMO radar[J].Journal of Electronics &Information Technology,2010,32(9):2197-2220.

[4]BENCHEIKH M L,WANG Y.Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar[J].Electronics Letters,2010,46(15):1081-1083.

[5]YAN H,LI J,LIAO G.Multitarget identification and localization using bistatic MIMO radar systems[J].EURASIP Journal on Advances in Signal Processing,2008,8(2):1-8.

[6]张剑云,郑志东,李小波.双基地MIMO雷达收发角及多普勒频率的联合估计算法[J].电子与信息学报,2010,32(8):1843-1848.ZHANG J Y,ZHENG Z D,LI X B.An algorithm for DOD-DOA and doppler frequency jointly estimating of bistatic MIMO radar[J].Journal of Electronics &Information Technology,2010,32(8):1843-1848.

[7]CHEN D F,CHEN B X,QIN G D.Angle estimation using ESPRIT in MIMO radar[J].Electronics Letters,2008,44(12):770-771.

[8]NIKIAS C L,SHAO M.Signal processing with alpha-stable distributions and applications[M].Wiley-Interscience,1995.

[9]宋爱民,邱天爽,佟祉谏.对称稳定分布的相关熵及其在时间延迟估计上的应用[J].电子与信息学报,2011,33(2):494-498.SONG A M,QIU T S,TONG Z J.Correntropy of the symmetric stable distribution and its application to the time delay estimation [J].Journal of Electronics &Information Technology,2011,33(2):494-498.

[10]张金凤,邱天爽,李森.冲激噪声环境下基于最大相关熵准则的韧性子空间跟踪新算法[J].电子学报,2015,43(3):483-488.ZHANG J F,QIU T S,LI S.A robust PAST algorithm based on maximum correntropy criterion for impulsive noise environments[J].Acta Electronica Sinica,2015,43(3):483-488.

[11]SANTAMARÍA I,POKHAREL P P,PRINCIPE J C.Generalized correlation function:definition,properties,and application to blind equalization[J].IEEE Transactions on Signal Processing,2006,54(6):2187-2197.

[12]LIU W,POKHAREL P P,PRÍNCIPE J C.Correntropy:properties and applications in non-Gaussian signal processing[J].IEEE Transactions on Signal Processing,2007,55(11):5286-5298.

[13]SIDROPOULOS N D,GIANNAKIS G B.Parallel factor analysis in sensor array processing[J].IEEE Transactions on Signal Processing,2000,48(8):2377-2388.

[14]RONG Y,VOROBYOV S A,GERSHMAN A B,et al.Blind spatial signature estimation via time-varying user power loading and parallel factor analysis[J].IEEE Transactions on Signal Processing,2005,53(5):1697-1710.

[15]LI L,QIU T S,SHI X F.FLOS-FPSD parameter estimation based on fractional power spectrum density in bistatic MIMO radar system under impulsive noise environment [J].Circuits Syst Signal Process,2016,35(9):3266-3283.

李丽（1979-），女，满族，黑龙江佳木斯人，博士，大连大学副教授，主要研究方向为阵列信号处理、参数估计。

邱天爽（1954-），男，江苏海门人，博士，大连理工大学教授、博士生导师，主要研究方向为数字信号处理理论及应用等。

贺明妍（1981-），女，山东烟台人，博士，大连大学讲师，主要研究方向为通信信号处理、高斯信号处理。

Novel method based on fractional lower-order correntropy-analogous statistics for parameter jointly estimation in bistatic MIMO radar

LI Li1,QIU Tian-shuang2,HE Ming-yan1
(1.Information Engineering College,Dalian University,Dalian 116622,China;2.Faculty of Electronic Information and Electrical Engineering,Dalian University of Technology,Dalian 116024,China)

According to the performance degradation problem of parameter estimation algorithm in the Alpha stable distribution noise,inspired by the concept of correntropy,a new class of statistics,namely,the fractional lower-order correntropy-analogous statistics (FCAS) was proposed.By employing the fractional lower-order correntropy-analogous statistics based cost function in parallel factor (PARAFAC),the FCAS-PARAFAC algorithm was deduced which can be utilized for the parallel factor under impulsive noise environments.The FCAS-PARAFAC algorithm was applied to parameter estimation in bistatic MIMO radar under impulsive noise environment.The proposed method can suppress the impulse noise interference and has better estimation performance.Furthermore,the estimated parameters are automatically paired without the additional pairing method.Simulation results are presented to verify the effectiveness of the proposed method.

bistatic MIMO radar,parameter estimation,fractional lower-order correntropy-analogous statistics,parallel factor,Alpha stable distribution

The National Natural Science Foundation of China (No.61401055,No.61671105)

TN911.7

A

10.11959/j.issn.1000-436x.2016236

2016-03-22；

2016-11-08

资助项目(No.61401055,No.61671105)