风电机组关键部件维修优化

文 | 翟长武，董玉亮



风电机组关键部件维修优化

文 | 翟长武，董玉亮

风电机组的高可靠性是风力发电的根本要求，然而潮湿、腐蚀、风沙、震动、极寒、极热等恶劣运行环境，不完善的运行控制策略和设计安装缺陷导致风力发电装置总体可靠性较低。较低的可靠性导致风电场运行与维护费用居高不下，据统计陆上风电场运行与维护费用占发电总成本的10％－20％。降低运行与维修费用主要有两个途径：一方面是应用状态监测技术进行故障的早期探测，减少事后维修；另一方面采用维修优化技术，获得最优的维护策略，降低维修费用。因此，开展风电机组关键部件维修策略优化研究，根据获得的最优策略合理安排维修，对提高风电机组运行安全性和可靠性，降低运行与维护费用具有重要的意义。

风电机组关键部件故障分析

典型的齿轮驱动风电机组结构如图1所示。

表1给出了齿轮驱动风电机组各系统故障率统计数据。可以看出，电气系统、变桨系统、风轮系统、传动系统、发电机系统、主控系统、监测系统、制动系统具有较高的故障率；而其中齿轮箱、发电机、风轮、主轴和主轴承的维修费用和停机损失远远高于其它部件。本文将齿轮箱、发电机、主轴和主轴轴承作为风电机组关键部件，对其维修策略进行优化。

关键部件主要故障模式和监测方法如表2所示。

风电机组关键部件维修策略优化模型

一、风电机组可靠性分析

风电机组可靠性分析流程如图2所示。

（一）可靠性数据收集

针对某一风电场的同类型风电机组，收集风电机组各关键部件的失效时间、失效前工作时间和失效原因，并按失效时间的先后顺序列表，作为可靠性统计分析时参数估计的数据。

（二）可靠性数据统计分析

目前在可靠性建模中应用比较广泛的模型有指数分布、正态分布、伽马分布、对数正态分布、威布尔分布和极值分布。本文采用极大似然估计的方法，拟合风电场设备的故障数据曲线，得到设备的故障率分布函数以及可靠度函数。下面以两参数威布尔分布函数为例，给出参数估计方法。

两参数威布尔分布概率密度为：

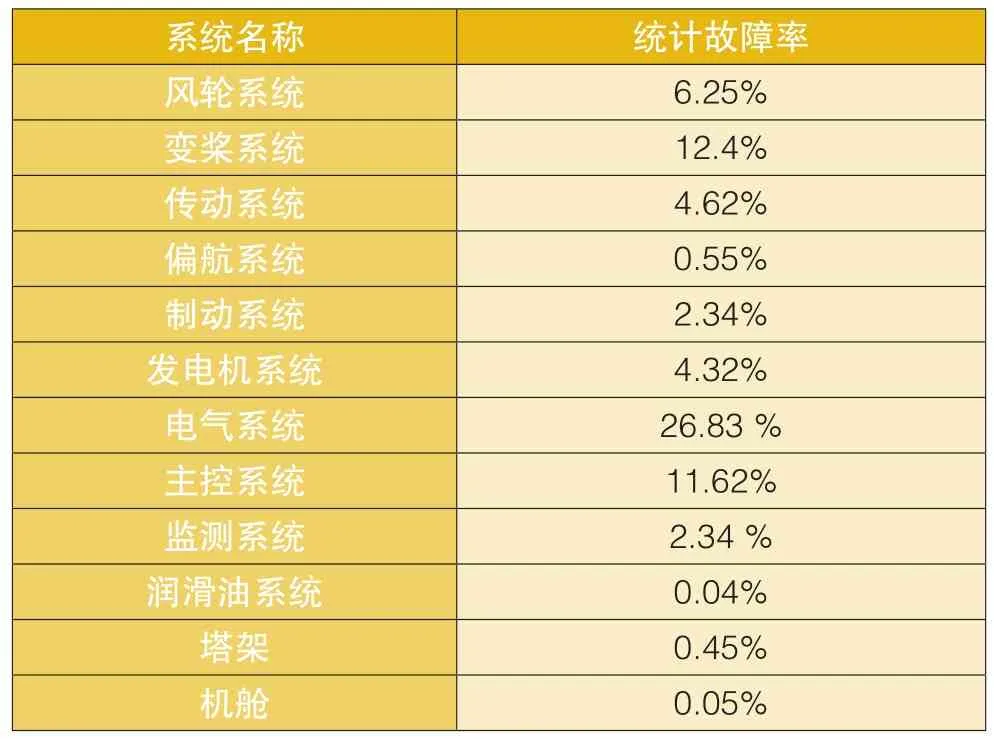
表1 风电机组各系统故障率统计表

故障率函数：

对于容量为n的完全样本数据x1≤x2≤…≤xm，取威布尔分布的对数似然函数：

根据式（4）式取得极大值时的β，γ的估计值，即可得到故障率的两参数威布尔分布。

（三）部件/系统可靠性计算

获得β，γ的估计值后便可用式（5）计算部件可靠度

利用建立的系统可靠性框图，便可计算系统不同工作时间的可靠度。

二、维修费用模型

风电机组进行以最小维修费用为目标的维修任务决策及优化，首先应建立维修/故障费用模型。一般地，维修/故障费用可分为预防维修费用、维修费用和故障维修费用。

（一）预防维修费用

预防维修费用指设备按照计划进行维修发生的维修费用，包括计划停运损失费用和预防维修材料、起重设备、人工费用。一次预防维修费用可表示为：

式中：Cploss－ 一次预防维修停运损失；Cpre－ 一次预防维修材料、起重设备及人工费用。

（二）机会维修费用

机会维修费用指设备进行机会维修（设备在非计划情况下维修，此时尚未出现功能故障）发生的维修费用，包括非计划停运损失费用和非计划维修材料、起重设备及人工费用。一次机会维修费用可表示为：

式中：Coloss－ 一次机会维修停运损失；Core－一次机会维修材料、起重设备、人工费用。

（三）故障维修费用

故障维修费用指设备进行故障维修发生的费用，包括故障停运损失费用和故障维修材料、起重设备及人工费用。一次故障维修费用表示为：

式中：Cfloss－故障维修停运损失；Cfre－故障维修材料、起重设备、人工费用。

通用的停运损失费用可以按式（9）计算：

式中：T－机组停运时间，包括部件购买运输时间、修理/更换时间；W－机组额定功率（kW）； f－功率因子；Cenergy－上网电价。

通用的维修费用：

式中：Cmaterial－材料费用；Ctrans－运输费用；Ccrane－起重机使用费用。

表2 风电机组关键部件故障模式分析

三、基于役龄的定期更换模型

定龄更换策略指设备或部件达到规定的使用间隔期（年龄）T，即使无故障发生也要进行预防性更换；如未到规定的使用间隔期T发生了故障，则对设备、部件作故障后更换。该策略适合于价格比较昂贵的设备及部件。

在已知部件的故障分布函数F（t）、一次故障维修费用Cf和一次预防维修费用Cp的条件下，可建立更换周期T内以单位工作时间维修/故障费用最小为目标的维修优化模型。

式中：Tj为可能的定期更换周期。

最优更换间隔可通过数值方法求解，给出一系列定期更换间隔Ti，带入式（11）得到对应的单位时间期望平均费用C(Ti），画出单位时间期望平均维修/故障费用随定期更换间隔变化而变化的曲线，便可得到最优的定期更换间隔。

为与风电场现行维修策略相比较，这里给出该类设备事后更换策略的单位时间平均维修/故障费用。设风电场现行定期更换周期为k年，则单位时间期望平均维修/故障费用可由式（12）得到：

当采用事后更换策略时，则设备/部件在（0,t）时间内的失效次数可用更新函数H（t）来确定。更新函数定义为在（0,t）时间内失效（更新）次数[N（t）]的数学期望。

对于事后更换，单位时间内期望平均维修/故障费用为：

可以证明，当t→∞时，有下式成立：

因此，单位时间内期望平均维修/故障费用可由式（16）计算：

式中：MTBF为设备平均无故障工作时间。

算例分析

以某风电场为例进行算例分析。该风电场由26台600kW风电机组组成。利用SCADA中故障历史数据，统计分析得到其关键部件的可靠性威布尔分布参数如表3所示。

风电机组故障/维修费用统计值如表4所示。

对各关键部件利用式（11），获得其单位时间平均维修/故障费用曲线，如图3－图8所示。

从图3－图8可以看出， 主轴和主轴承没有最优更换间隔期，而齿轮箱齿轮、高速轴轴承、中速轴轴承、中速轴轴承和发电机轴承具有最优更换间隔期。表5列出了各部件分别采用最优间隔更换策略和故障更换策略的平均维修/故障费用。可以看出齿轮箱和发电机关键部件采用优化的定期更换策略可以大大降低平均维修/故障费用。

表3 风电机组关键部件故障模式分析

表4 风电机组关键部件维修费用

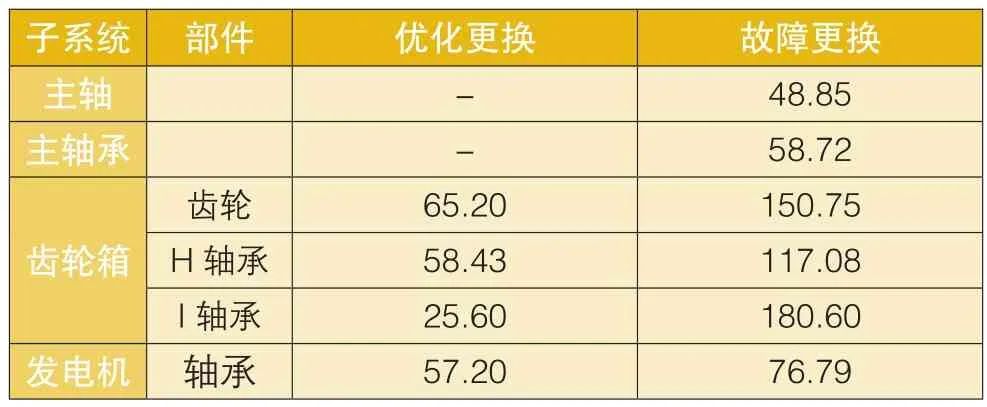
表5 风电机组关键部件平均维修/故障费用（元/天）

结语

居高不下的风电机组维护费用增加了风电场的运营费用。本文针对风电机组关键部件建立了可靠性分析模型、维修费用模型和定期更换模型。通过仿真计算，确定了关键部件的维护策略，给出了相关部件的最优更换间隔期。采用优化后的维护策略可以大大降低机组的平均维修/故障费用。

（作者单位：翟长武：张家口供电公司下花园客户服务分中心；董玉亮：华北电力大学能源动力与机械学院）