正规文法与有穷自动机的等价性研究
2016-06-18李忠武保山学院云南保山678000
李忠武 保山学院 云南保山 678000
正规文法与有穷自动机的等价性研究
李忠武 保山学院 云南保山 678000
【文章摘要】
正规表达式首先由Keene在20世纪50年代开始研究。McCullough和Pitts提出了一种描述神经活动的有穷自动机模型,从此以后,正规表达式和有穷自动机在计算机科学中得到了广泛应用。通常,对于正规文法G 和有限自动机M ,M 所定义的语言记作L(G),M 所能识别的语言记作L(M),如果有L(G)=L(M),则称G 和M是等价的。
【关键词】
正规式;正规文法;构造方法;等价性;有限自动机
引言
正规表达式的递归定义
(2)如果a是∑上的一个符号,那么a是一个正规表达式,并且。也就是说,这个语言仅包含一个长度为1的符号串a 。
(3)假定U和V都是∑上的正规表达式,分别表示语言为L(U)和L(V),那么,U |V、 U·V和(U)*也都是正规式,它们所表示的正规集分别为L(U)∪L(V)、L(U)L(V)(连接积)和((闭包)
仅由有限次使用上述三步骤而定义的表达式才是∑上的正规式。
有穷自动机的定义
有限自动机是识别器,只能对每个可能的输入串简单回答“是”或“否”。它分为不确定的有穷自动机和确定的有穷自动机。
正规文法的概念
文法G 可定义为四元组
1 正规文法与有限自动机的等价性
对于正规文法G 和有限自动机M ,如果L(G)=L(M)f,则称G和M是等价的。
关于它们两者的等价性,有以下结论:
1.对于每一个右线性正规文法G或左线性正规文法G ,都存在一个有限自动机,使得L(M)=L(R)。
证明1:

则令。与(1)类似。可以证明。
证明2:

因而,在M中有一条从S0出发依次经过A1,...,AK-1到达终态的通路,该通路上所有箭弧的标记依次为a1,...ak。反之亦然。所以,当且仅当。
现在考虑S0F的情形
所以,在上述GR中添加新的非终结符号t',t'S和产生式,并用t'代替t作开始符号。这样修正GR后得到的文法GR'仍是右线性正规文法,并且。
(2)类似于(1),从NFA M出发可构造左线性正规文法GL,使得。
最后,由DFA和NFA之间的等价性,结论2得证。
2 等价性应用举例

图1 状态转换图
(a)初始的转换图;(b)从等价的右线性正规文化导出的转换图
GR=<{0,1},{A,B,C,D},A,P>,其中P由下列产生式组成:
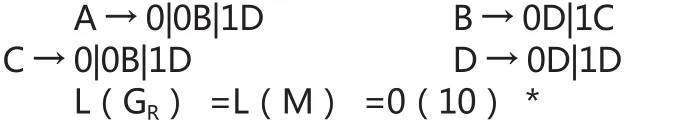
NFA M出发构造左线性正规文法GL=<{0,1},{B,C,D,f},f,P>,其中P由下列产生式组成:

易证L(GL)=L(M)。
3 结束语
有限自动机状态转换图的形式化表示。它指是一个开始状态、一个或多个接受状态,以及状态集、输入字符和状态间的转换集合。接受状态表明已经发现了和某个词法单元对应的词素。有限自动机即可以在输入字符上执行转换,也可以在空输入上执行转换。
正规式是正规文法、有穷自动机FA的代数化表示,它的表示准确、紧凑、高效,可以构造高效的词法分析器.用于词法分析器的自动生成,也用于各种信息(如模式识别、情报检索。
状态转换图是正规文法、有穷自动机FA的图形表示,直观易懂,与通常的程序流程图很相近,易于实现程序的编制。
【参考文献】
[1]陈火旺,刘春林,谭庆平,赵克佳,刘越.程序设计语言编译原理[M]. 北京:国防工业出版社,2013: P53.
[2]葛寒松.正规文法与有限自动机的等价性研究[J]. 河南:商丘师范学院学报,2010,26(12):P75.
[3]胡元义.编译原理教程(第2版)[Z]. 西安:西安电子科技大学出版社, 2006.
