闽楠天然林林分结构规律的研究
2016-06-18林笑雨黄思猷唐巧倩江希钿
林笑雨,黄思猷,唐巧倩,江希钿
(福建农林大学林学院,福建福州350002)
闽楠天然林林分结构规律的研究
林笑雨,黄思猷,唐巧倩,江希钿
(福建农林大学林学院,福建福州350002)
摘要:利用闽楠天然林样地调查数据,对其林分结构规律进行研究。研究结果得出:闽楠天然林的林分直径分布呈中间高两边低的不对称山状曲线,可用威布尔概率密度函数进行拟合。在同一树高阶内,直径分布也基本呈不对称山状曲线,均可用对数正态分布函数、伽玛分布函数和威布尔概率密度函数进行拟合检验。林分树高分布呈贝塔分布,最高的树木为平均高的1.74倍,最矮的树木为平均高的0.29倍,变动系数31.88%,说明闽楠天然林林分树高的变动幅度较大。在同一径阶内,树高分布也是呈不对称山状曲线,用贝塔分布函数和威布尔分布函数拟合效果最好,其次是正态分布函数。径阶内的最小树高为径阶平均高的0.38~0.75倍,最大树高为径阶平均高的1.28~1.58倍,其树高变动幅度小于整个林分,且随径阶加大树高变动幅度逐渐缩小。研究闽楠天然林林分结构规律,对保护和利用其森林资源有着重要意义。
关键词:闽楠;结构规律;直径分布;树高分布
楠木,为中亚热带常绿乔木,最高可达约30 m,胸径可达1 m,主指桢楠属(Phoebe nees)和润楠属(Machilus nees)木材[1]。桢楠归类为楠木本类,主要有闻香园林金丝楠,缅甸黄楠,小叶楠等;润楠归类为楠木旁类,主要有水楠,大叶楠,滇楠,紫楠等。楠木为樟科常绿大乔木,国家二级保护渐危种,分布区于亚热带常绿阔叶林区西部,气候温暖湿润,生长在气温约0~38℃,年降水量为1 400~1 600 mm的亚热带区域[2],楠木是驰名中外的珍贵用材树种,在我国贵州、四川、重庆、湖北等地区有天然分布,是组成常绿阔叶林的主要树种。本文利用闽楠天然林标准地材料,对其林分结构特征进行研究,为掌握闽楠天然林的林分结构规律提供科学依据。
1 试验地概况
试验地位于福建省三明市明溪瀚仙镇连厝村沙洲坑甲自然保护小区,位于北纬26°08'~26°39',东经116°47'~117°35'。平均海拔高度200~300 m之间,属亚热带海洋性季风气候,年平均气温18℃,年平均降雨量1 800 mm,年平均无霜期261 d,气候温和,雨量充沛,冬少严寒,夏无酷暑,光照充足。
试验地上的闽楠天然林为异龄林,乔木层主要以闽楠为主,还混生有苦椎、枫香、樟树等。林下植被丰富,种类繁多。灌木层主要有桂花幼树、芒萁、小叶石楠,楠木幼树等,灌木密度约为50%~60%。草本层主要有络石,常青藤,凤尾蕨,石松,麦冬,显齿蛇葡萄,韭厥,夹迷,石栎,豆崖藤,水芋,木苺,蓑草,鸢尾,次雪丹,老鼠矢,铁线莲等。
2 研究方法
2.1 资料收集和整理
在福建省三明市明溪瀚仙镇连厝村沙洲坑甲自然保护小区的闽楠天然林林分内,选择有代表性的地段设置100 m×100 m的样地,并在所选择的样地范围内对所有活立木进行每木调查,测定每株树木的直径、树高等测树因子,其中所测直径为胸径,即乔木主干离地表1.3 m处直径大小[3]。按直径4 cm、树高2 m的组距将样地的每株树木进行归组统计(见下表),以此作为研究闽楠天然林林分结构规律的基本数据。

表1 每木卷尺数据统计情况
利用ExceL软件,对所测直径和树高进行数据整理,并根据其与株数之间的关系分别绘制折线图,得到图1、图2。
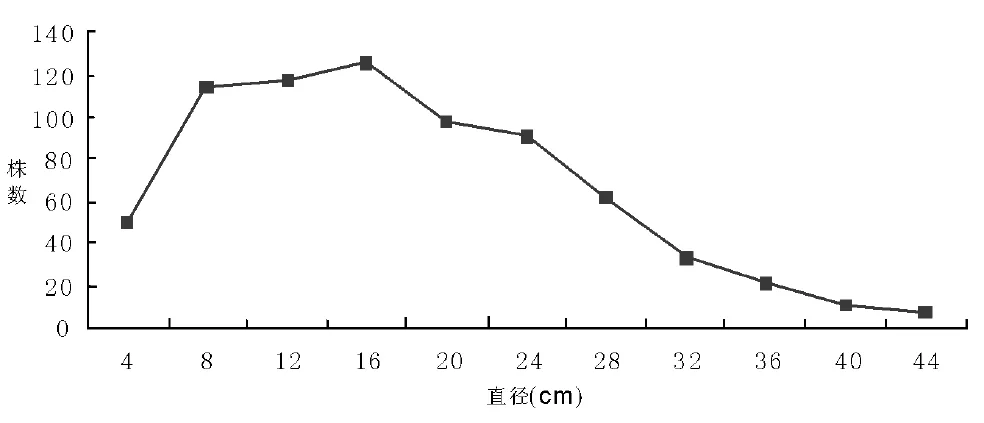
图1 株数与直径关系图

图2 株数与树高关系图
2.2 概率密度函数
采用概率密度函数描述闽楠天然林林分的直径和树高分布规律[4-5]。为适应不同情况下的闽楠天然林直径分布和树高分布形状变化的特点,选用的函数需有较大的灵活性[6],其主要表现在函数对偏度和峰度变化的适应力上,以下采用五种的概率密度函数描述闽楠天然林林分的直径和树高分布规律。
(1)正态分布的概率密度函数:

(2)对数正态分布的概率密度函数:
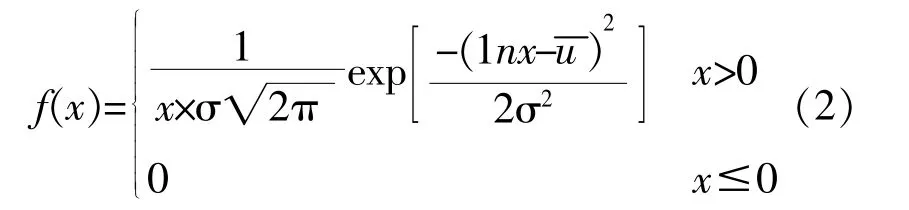
式中:u为随机变量Lnx的平均数;σ为随机变量Lnx的标准差。
(3)WeibuLL分布密度函数:

式中:a为位置参数;b为尺度参数;c为形状指数。
(4)Г分布的概率密度函数:

式中:α为形状参数;β为尺度参数。
数学期望E(x)和方差V(x)分别:

Г分布是适应性比较强的概率分布,当α=1时,Г分布为指数分布,当α=,β=时,Г分布为卡平方分布[7]。
(5)β分布的概率密度函数

其中,参数α,β决定了其分布曲线类型和形状。
一个林分的直径分布究竟服从什么分布类型,应进行统计假设检验。最常用的检验方法有x2检验和柯尔莫哥洛夫检验[8]。x2检验是以林分总体为对象。柯尔莫哥洛夫检验则是以径阶累积频数样本值与相应理论值的偏差大小作为依据作出检验判断,比x2检验精确。但一般情况下,这二种检验方法的结论是一致的,所以通常采用x2检验。
此外,可用于说明林分直径和树高分布的特征数还有:变动系数,反映分布范围大小,其值大则离散程度大[9];偏度,大于0为左偏,小于0为右偏;峰度,其值愈大,概率密度曲线愈尖峭,反之愈平坦[10]。
3 结果分析
3.1 直径结构规律
3.1.1 林分直径分布
闽楠天然林属于异龄林,异龄林林分直径结构比同龄林分要复杂,其分布受林分年龄结构、树种特性及组成、更新方式及过程、自然灾害、采伐方式及强度、立地条件等多种因素影响,其直径分布呈近似中间高两边低的不对称山状曲线,即林木株数一开始随着直径的增加而增加,16 cm径阶时达到最大值,之后随着直径的增大,林木株数开始减小,最后趋于平缓。
闽楠天然林林木株数和直径的变化特性为:小径阶时林木株数随直径增加而增加,到达16 cm径阶时林木株数到达最大,而后随直径增加而减少,呈现不对称山状曲线。用五种概率密度函数进行拟合,通过计算得出各函数的卡方值:正态分布为50.06,对数正态分布为42.37,威布尔分布为5.34,伽玛分布为29.51,贝塔分布为27.80,临界值为15.51,结果显示,只有威布尔分布函数能够通过检验,各参数为:a=2.729,b=17.715,c=1.803,x2=5.338<x=15.507。x2检验表明,闽楠天然林的直径分布服从威布尔分布。
3.1.2 各树高阶直径分布
各树高阶的直径分布指在林分同一树高阶内各径阶的林木株数[11]。各树高阶的直径分布在树高阶小于8 m树高阶时,株数随直径增加而减小。但其它各树高阶的直径分布则是均呈中间高两边低的非对称山状曲线。现用五种概率密度函数拟合各树高阶的直径分布,并计算平均值、标准差、变动系数、偏度、峰度等特征值,结果如下表所示。

表2 林分直径分布检验数据和结果
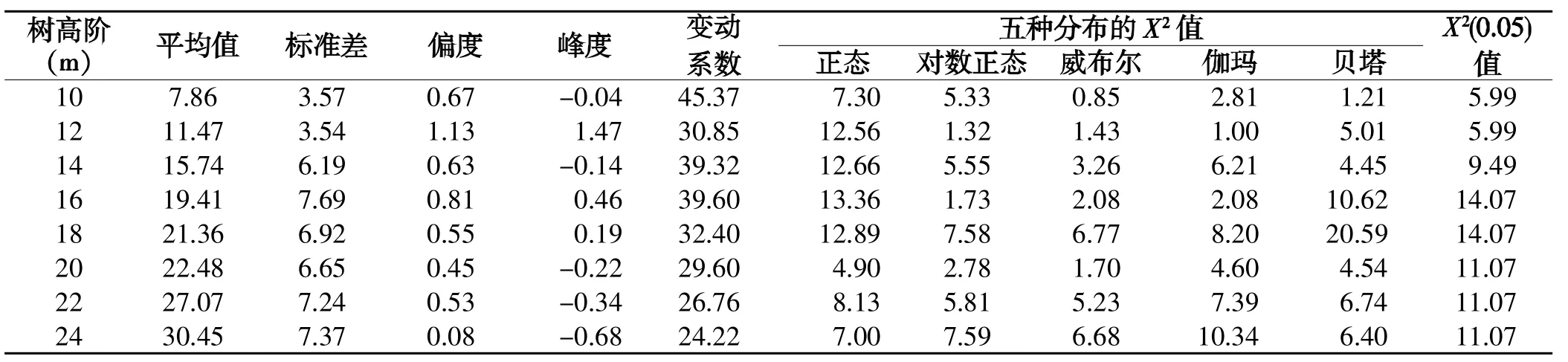
表3 各树高阶直径分布检验结果
由表3可知,各树高阶的直径分布用对数正态分布函数、伽玛分布函数和威布尔概率密度函数拟合效果都相对较好,各树高阶均能通过卡方检验,拟合率达100%。说明这三种分布函数既可以拟合山状曲线,也可以拟合下降曲线,具有良好的适应性。各树高阶的直径分布拟合效果其次的是贝塔分布,只有一个树高阶不能通过卡方检验,拟合率为83.3%。而正态分布函数有3个径阶未能通过卡方检验,拟合率仅为38%,在五个分布函数中通过率是最小的。

图3 变动系数与树高关系图
各树高阶的直径变动系数均在20%以上,未超过46%。各树高阶内的最细树木为树高阶平均直径的0. 38~0.64倍,最粗树木为树高阶平均直径的1.31~2.10倍,说明在同一树高阶内,闽楠天然林直径变化的离散程度较大。由图3看出,不同树高阶的直径变动幅度之间的差异主要体现在,树高阶小,相对直径的变动幅度大;树高阶大,则相对直径的变动幅度小。
从偏度来看,各树高阶的偏度为正,其直径分布为左偏。而各树高阶的峰度则有正有负,表明各树高阶的直径分布和标准正态分布曲线相比,有的平缓有的尖峭。

表4 林分树高分布检验数据和结果
3.2 树高结构规律
3.2.1 林分树高分布
林分树高分布是指整个林分各树高阶的林木株数,尽管林分内各株树木的树高不同,但从总体上看,以中等高度的树木占大多数,向两端树高阶逐渐减少,呈中间高两边低的山状曲线[12]。现用五种概率密度函数进行拟合,得到如下结果。
通过计算得出,用五种概率密度函数进行拟合闽楠天然林林分树高分布规律,其卡方值分别如下:正态分布为56.21,对数正态分布为338.35,威布尔分布为130.25,伽玛分布为1797.97,贝塔分布为102.02,临界值为18.31,结果显示,所有概率密度函数都不能通过卡方检验,其中正态分布和贝塔分布的卡方值最接近于临界值,于是将两者进行误差分析,根据平均误差显示,贝塔分布的平均误差相较于正态分布的平均误差更小,故可认为贝塔分布最适合闽楠天然林林分树高分布规律。
林分树高若以平均高为准,则林分最高的树木为平均高的1.74倍,最矮的树木为平均高的0.29倍。若将林分平均高看作1,用相对值表示,则林分树高的变动范围为0.29~1.74,变动系数31.88%,说明闽楠天然林林分树高的变动幅度较大。林分树高的偏度为-0.36,表明树高颁布曲线为右偏。峰度为-0.37,说明闽楠天然林林分树高分布曲线略为平坦。
3.2.2 各径阶树高分布
径阶树高分布是指在林分同一径阶内各树高阶的林木株数。各径阶的树高分布规律与整个林分基本一致,变化趋势均呈中间高两边低的非对称山状曲线。现用五种概率密度函数拟合各径阶的树高分布,并计算平均值、标准差、变动系数、偏度、峰度等特征值,结果如表5所示。
由表5可知,各径阶的树高分布用贝塔概率密度函数和威布尔概率密度函数检验效果最好,各径阶均能通过卡方检验,检验率达100%。其次是正态分布,只有一个径阶未能通过卡方检验,检验率达88%。用对数正态分布进行检验有6个径阶的树高分布均能通过卡方检验,检验率达75%,而伽玛分布函数只有2个径阶通过卡方检验,检验率仅25%,在五个分布函数中效果最差。

图4 变动系数与径阶关系图
从图4中可以看出,树高变动系数大体上随径阶增加而减小。以径阶平均高为基准,径阶内的最小树高为径阶平均高的0.38~0.75倍,最大树高为径阶平均高的1.28~1.58倍。若将径阶平均高看作1,则径阶内的树高变动范围为0.38~0.75至1.28~1.58。显然,径阶内的树高变动幅度小于林分的树高变动幅度,但不同径阶的树高变动幅度存在差异,从整体上看,径阶越小,树高变动幅度越大,即随径阶加大树高变动幅度逐渐减小,之后趋于平缓。
从表中看出16、24、32 cm径阶的偏度为负,其余径阶的偏度为正,说明各径阶的树高分布大多数为左偏。从峰度来看,所有径阶为负,表明各径阶的树高分布曲线较为平缓。
4 结论
闽楠天然林的直径分布和林分树高分布均呈中间高两边低非对称山状曲线,其中直径分布主要表现在,闽楠天然林的株数一开始随直径增加而增加,到达16 cm径阶时,其株数到达最大值,之后随直径增加株数逐渐减少,最后趋于平缓;而林分树高分布情况则是,林木株数一开始随树高增加而增加,而树高到达18 m高阶时,其林木株数到达最大值,之后株数随树高增加而逐渐减少,最后趋于平缓。
其各径阶树高的分布规律与整个林分基本一致,变化趋势均呈中间高两边低的非对称山状曲线,而各树高阶的直径分布在树高阶小于8 m树高阶时,株数随直径增加而减小,其它则是呈现中间高两边低的非对称山状曲线,可视其实际情况分别用正态分布、威布尔分布和贝塔分布函数描述。

表5 各径阶树高分布检验结果
本研究的缺陷在于,考虑到由于所研究的闽楠天然林所处的地理位置和地形较为复杂,不同地段、地势的林木接受水分和光照都会受到不同程度的影响,导致不同年龄段的林木在树高分布和直径分布上不一定那么均匀精确,所以会出现少许波动,但总体上没有太大影响。
研究闽楠天然林林分结构规律,对于了解其生长状态、生长收获预估和经营管理都具有一定的指导意义。
参考文献:
[1]刘志雄,费永俊.我国楠木类种质资源现状及保育对策[J].长江大学学报(自然科学版),2011(5)∶221-223.
[2]贾贤,黄秋生,刘光华,等.我国楠木资源的研究现状[J].中国园艺文摘,2014(10)∶55-59.
[3]孟宪宇.测树学[M].北京∶中国林业出版社,1996∶188-216.
[4]金星姬,李凤日,贾炜玮,等.树木胸径和树高二元分布的建模与预测[J].林业科学,2013(6)∶74-82.
[5]Wang Lingzhi,Qian Fucai.Technique of ProbabiLity Density Function Shape ControL for NonLinear Stochastic Systems[J]. JournaL of Shanghai Jiaotong University(Science),2015(2)∶129-134.
[6]徐洪香,刘秀娟.以创新应用能力为核心的概率统计课程教学模式的探索与实践[J].辽宁工业大学学报(社会科学版),2013(4)∶137-139.
[7]Yan Zaizai,Ma JunLing,Nie Zankan. A new estimate of shape parameter in the famiLy of gamma distribution[J]. AppLied Mathematics∶A JournaL of Chinese Universities,2000(4)∶419-424.
[8]孙红卫,董兆举,赵拥军.对统计假设检验的误解与误用[J].中国卫生统计,2012(1)∶147-148.
[9]王文森.变异系数∶一个衡量离散程度简单而有用的统计指标[J].中国统计,2007(6)∶41-42.
[10]田禹.基于偏度和峰度的正态性检验[D].上海∶上海交通大学,2012.
[11]徐海,赵中华,陈瑞生,等.贵州天然阔叶混交林不同径阶林木的空间分布特征分析[J].贵州林业科技,2011(4)∶10-17.
[12]刘发林.南方集体林区木荷次生林生长规律及经营技术研究[D].长沙∶中南林业科技大学,2013.
(责任编辑:华伟平)
Studies on the Stand Structure of Machilus Natural Forest in Fujian
LIN Xiaoyu,HUANG Siyou,TAN Qiaoqian,JIANG Xidian
(SchooL of Forestry,Fujian AgricuLture and Forestry University,Fuzhou,Fujian 350002)
Abstract:Based on the SampLe-pLot survey data in Fujian machiLus naturaL forest,studies on it's stand structure. The ResuLts showed that∶The distribution of the diameter distribution on Fujian MachiLus naturaL forest is present on a asymmetric montiform curve that the middLe is higher than those of the sides. it can fitting by weibuLL distribution. In the same height grade,The distribution of the diameter distribution is aLso present on a asymmetric montiform curve,it can fitting by normaL distribution,normaL distribution and weibuLL distribution. The distribution of the height distribution is present on beta distribution,the taLLest tree is 1.74 times higher than the average,the shortest tree is 0.29 times higher than the average,the coefficient of variation is 31.88%,it iLLustrates that the ampLitude of fLuctuation of naturaL forest of Fujian machiLus Stand height is big. In the same diameter grade,The distribution of the height distribution is present on a asymmetric montiform curve,it can fitting by beta distribution and weibuLL distribution for optimum resuLts,and the second is normaL distribution. And the minimum tree is 0.38~0.75 times higher than the average in the same diameter grade,the maximum tree is 1.28~1.58 times higher than the average,the ampLitude of fLuctuation of the height is Less than the entire stand's,and it wiLL graduaLLy narrowing with the diameter increasing. Studies on the stand structure of Fujian MachiLus naturaL forest is important to protect and use its forest resources.
Key words:Fujian machiLus,stand structure,diameter distribution,height distribution
中图分类号:S757.3
文献标识码:A
文章编号:1674-2109(2016)03-0023-06
收稿日期:2015-12-23
基金项目:福建省自然科学基金项目(B0010019)。
作者简介:林笑雨(1990-),男,汉族,在读硕士研究生,从事森林经理学研究。
通讯作者:江希钿(1958-),男,汉族,教授,博士生导师,从事森林经营与资产评估研究。
